基于零陷展宽并加深的高动态GNSS抗干扰算法
2020-04-23丛玉良李宏磊
丛玉良,冯 达,2,李宏磊
(1.吉林大学 通信工程学院,长春130012;2.中国人民解放军 91388部队,湛江 524000;3.中国人民解放军 63782部队,哈尔滨 150039)
0 引 言
全球导航卫星系统(GNSS:Global Satellite Navigation System)是指一种以人造地球卫星为导航平台的星基无线电导航系统[1],随着军事现代化的不断升级,GNSS会越来越密集地应用到高精度武器装备上,随着新型武器的出现,如超高音速战斗机、巡航(弹道)导弹等经常处于高动态的作战环境,所搭载的导航接收机也同样处于高速运动状态[2]。由于接收机平台不稳定,常规的自适应抗干扰技术很难应对干扰来向的快速变化,即使计算出上一时刻的干扰来向,也很难跟踪下一时刻干扰的来向。在高动态条件下,传统静态下或低动态下的抗干扰手段几乎全部失效。
传统抗干扰技术主要建立在稳定阵列平台基础上。由于零陷技术是在干扰方向上形成稳定的波束零陷,与干扰信号产生对消,阵元数越多,零陷就越窄越深,对平台的稳定性要求极其敏感。若因阵列不稳定而导致零陷指向误差,致使零陷最深位置偏离干扰来向,则零陷技术的性能将严重降低。零陷展宽技术[3-6]的出现,较好地解决了这一问题。
目前解决零陷指向误差都基于等距直线阵,主要分为两种方法:一种是利用采样协方差矩阵估计获取干扰信号的DOA(Direction of Arrival),再对加权矢量增加约束,求出修正后的加权矢量[7-8],如Mailloux[3]提出用虚拟的若干离散干扰源取代原来实际存在的干扰源,自适应波束会在每个离散虚拟干扰源处形成数量较多的零陷,以此达到展宽零陷的目的。但由于干扰离散后的总增益不变,使各个虚拟干扰源的功率小于原独立干扰源的功率,因而导致零陷深度变浅[9];Zatman[4]提出将原始窄带干扰信号替换为对应的宽带干扰信号,以此达到展宽零陷的目的;Guerci[10]归纳总结了上述2种零陷展宽方法,并统称为协方差矩阵锥化(CMT:Covariance Matrix Taper)法,同时系统分析出了零陷变浅的主要成因;另一种是假定干扰来向服从某种统计分布,构造锥化矩阵对阵列接收数据的协方差矩阵进行扩展加权,达到零陷展宽的目的。武思军等[5]从空间干扰导向矢量服从某种分布的角度,研究了一种自适应的展宽零陷方法;程乃平等[11]研究提出CMT算法的递推实现方法,降低了CMT算法的复杂度,并将该算法与对角加载技术相结合,从而提高了算法的稳健性。此外,近几年出现了很多非CMT类零陷展宽方法,Amar等[12]提出了基于线性约束区域响应抑制的波束约束;李文兴等[13]提出了基于投影变换和对角加载的波束形成零陷展宽方法;Qian等[14]及Mao等[15]提出了基于相似性约束和协方差矩阵重构的零陷展宽方法,这些方法都需要预知干扰的先验信息。
CMT算法是一种经典的波束形成零陷展宽方法,实现简单且计算量小,也不需要知道干扰来向的先验信息。但CMT算法的缺点在于零陷展宽的同时深度会也会变浅,使滤波处理后的干扰剩余量较多,削弱了对干扰的抑制效果。针对该问题,笔者在CMT算法基础上,提出一种零陷展宽并加深的方法。所提算法基于干扰扰动统计模型服从高斯分布的思想,结合功率倒置算法原理,将特征子空间投影方法与该算法相结合,通过子空间投影变换的方法提取接收数据中的干扰分量,再经过加权处理构造新的数据信息,达到增强干扰的目的[16],从而在零陷展宽的基础上增加了零陷深度。
1 基于高斯分布的零陷展宽算法原理
下面以一种基于统计模型的自适应波束零陷展宽方法,在高动态条件下,干扰来向变化符合高斯分布统计规律,称为G-NW(Gaussian-Nulling Widening)算法。
1.1 信号模型
考虑一阵元数为M等距线阵,阵元间距d为半波长λ/2(λ为单频导航信号波长),假设阵列接收一个卫星信号和K(K X(t)=a(θ0)s0(t)+AS(t)+N(t) (1) 其中s0(t)为卫星导航信号,a(θ0)为卫星信号对应的导向矢量,N(t)为高斯白噪声向量,S(t)为干扰信号,S(t)=[s1(t),s2(t),…,sP(t)]T,A=[a(θ1),a(θ2),…,a(θM)]为干扰信号导向矢量阵,其中a(θp),p=1,2,…,K为第K个干扰信号对应的导向矢量,可表示为 a(θp)=[1,ejφp,e2jφp,…,ej(N-1)φp]T (2) 其中φp=2πdsinθp/λ为相邻阵元间相位差,[·]T为矩阵转置。则理论协方差矩阵为 (3) 其中rp为第p个干扰信号功率,σ2为阵列噪声信号功率,IM为M×M维单位矩阵。 利用功率倒置算法求解下列优化问题获得最优加权矢量w (4) 其中w=[w1,w2,…,wM]T为加权矢量,s为目标导向矢量,s=[1,0,…,0]T,R为协方差矩阵。利用拉格朗日方程可求得最优自适应权值为 wopt=(sHR-1s)-1R-1s=vR-1s (5) 其中v=(sHR-1s)-1为常数。由于PI(Power Inversion)算法在干扰入射方向上形成的零陷较窄,在高动态GNSS平台中,采用批处理计算权值较慢导致指向存在偏差,其干扰抑制性能将大大降低,甚至失效。 基于上述考虑,假设在初始干扰入射方向θp上增加一个扰动角Δθp,Δθp的单位为(°)。则 (6) Δθp∈N(0,ξp) (7) (8) (9) (10) 其中IK×K表示K×K的全1矩阵,f(up)表示up的概率密度函数,则Rp的第(n,l)个元素(n=1,2,…,N;l=1,2,…,N)为 (11) 由式(10)可以得到 (12) (13) 矩阵T把干扰扰动Δθp的作用计算入协方差矩阵Rp,由Rp得到新的最优权值w,使零陷在干扰方向上展宽。此时, (14) (15) (16) 在G-NW算法的基础上,为了解决零陷深度不足的问题,提出一种基于高斯分布的零陷展宽并加深(G-NWD:Gaussian-Nulling Widening and Deepening)算法。所提算法假定高动态GNSS信号与干扰信号角度之间在可分辨范围内。 对式(12)中权值训练期间干扰协方差矩阵进行特征值分解,得 (17) span{a(θ1),…,a(θK)}=span{u1,u2,…,uK} (18) 将接收到的数据进行投影变换,提取干扰分量,剔除噪声分量,再进行加权处理,得到更新后的数据采样 (19) 根据特征子空间性质,求出干扰子空间的投影矩阵 (20) 式(19)中,g为干扰加深参数,即能加深干扰信号分量的参数,干扰分量在加权后功率变为原来的(1+g)2倍,单位为dB。由于g决定了干扰信号的增加量,可根据实际GNSS接收机运行工作状态,选择g的值。 最终,新的干扰噪声协方差矩阵为 (21) 其中 (22) 将新的协方差矩阵代入功率倒置算法,实现对干扰零陷的有效展宽并加深。 (23) 为模拟高动态仿真环境,设置干扰扰动参数ξmax=0.1°,零陷加深参数g取10。采用阵元数为7的等距线阵,阵元间距为半波长,快拍数为500,窄带干扰的入射角度为0°,两个入射信号为互不相关。干扰信号输的入干噪比60 dB,输入噪声为高斯白噪声。 图1为干扰入射角为0°时的PI算法、G-NW算法和G-NWD算法波束比较图,其中,图1b为零陷局部放大图。当干扰扰动参数ξmax=0.1°,零陷加深参数g取10时,G-NWD算法零陷深度比G-NW算法深约9 dB。假设在高动态环境下因计算权值更新不及时,导致计算角度偏差1°时,如图1b所示,此时PI算法、G-NW、算法和G-NWD算法对应零陷深度为-19.32 dB、-50.49 dB和-61.82 dB。零陷的深度和宽度都是最好的,因此对于高动态环境下扰动干扰的抑制效果越佳,而G-NWD算法在G-NW算法的基础上增加加深参数g的计算量很小,可以忽略不计。综上分析,G-NWD算法提高了G-NW算法性能,解决了零陷展宽后变浅的问题。 a 波束比较图 b 局部放大图 仿真条件为:阵元数为7的等距线阵,阵元间距为半波长,快拍数为500,窄带干扰入射角为0°,输入干噪比60 dB,加深参数g=1。图2a为干扰扰动参数ξmax取值分别为0.1°,0.5°和2°时G-NWD算法的波束比较图。图2b为图2a的局部放大图。 a 波束比较图 b 局部放大图 从图2可看出,随着ξmax的增大,零陷的宽度也在不断增大,同时零陷的深度也逐渐变浅,当ξmax=2°时零陷底端有齿状波动,干扰性能减弱,说明零陷宽度并不是越宽越好,干扰扰动参数需要根据实际进行取值,以追求算法的稳健性。 仿真条件:阵元数为7的等距线阵,阵元间距为半波长,快拍数为500,窄带干扰入射角为0°,输入干噪比60 dB。假设干扰扰动参数ξmax=0.1°,图3a为加深参数g分别取1、10和20时,对应G-NWD算法的零陷比较图。图3b为局部放大图。 由图3可明显看出,g的取值越大,零陷深度也越深。 下面分析加深参数g的最优取值。最佳加深参数g应是使输出干噪比最小时所对应的g。根据前述仿真条件,高动态条件下,因权值计算时延导致的计算角度偏差为1°,为了得到最佳g,仿真采取g取值从1~100时,PI算法和G-NWD算法对应的输出干噪比,输出干噪比越小,算法干扰性能越好,计算数据如表1所示。 由表1数据可知,随着g的增大,G-NWD算法能改善PI算法的干扰抑制性能。但当g增大到10后,虽然零陷深度仍在增加,由于干扰扰动参数固定,限制了干扰波束的宽度,因此输出的干噪比趋于平稳。所以,通过增大加深参数g,对提高算法抗干扰性能是有限的。 a 波束比较图 b 局部放大图 表1 加深参数g与输出干噪比关系 综上分析,G-NWD算法在高动态的具体应用中,应根据实际运动状态、权值计算复杂度以及阵列阵元数等条件,先计算干扰扰动参数ξmax最优取值,再设置合理的加深参数g,使G-NWD算法抗干扰性能达到最佳。 在高动态条件下,因导航接收机算法处理时存在一定时间消耗,因此每次计算的权值可能跟不上实际干扰方向变化的速率,导致干扰角度计算结果与实际方向存在一定偏差,因此需要研究计算角度偏差对算法产生的影响。 PI算法权值计算的复杂度为O(N3),由式RCMT=Rx⊙TCMT可知,Hadamard积“⊙”的计算复杂度为O(N2),因此,G-NW算法的计算复杂度比PI算法增加了1/N,即在相同的高动态条件下,G-NW算法比PI算法增加了1/N的角度偏差;由于G-NWD算法需要求取特征值,根据QR分解求矩阵特征值的计算复杂度为O(N2),因此,G-NWD算法比G-NW算法又增加了1/N的角度偏差。对七元直线线阵,若PI算法角度偏差为1°,则G-NW算法的角度偏差约为1.14°,G-NWD算法的角度偏差约为1.28°。 仿真条件:阵元数为7的等距线阵,阵元间距为半波长,快拍数为500,窄带干扰入射角为0°,输入干噪比60 dB。干扰扰动参数ξmax=0.1°,加深参数g=10。为研究G-NWD算法输出干噪比与计算角度偏差之间的关系,干扰抑制性能可用输入输出干噪比(INR:Interference to Noise Ratio)的变化百分比表示 干扰抑制性能=(输入INR-输出INR)/输入INR×100% (24) 表2为PI算法、G-NW算法和G-NWD算法的计算角度偏差与输出干噪比关系的部分计算数据。图4为计算角度偏差从0°~1.8°输出干噪比曲线图。 表2 计算角度偏差与输出干噪比的关系 从图4和表2可以得出以下结论: 图4 计算角度偏差与输出干噪比之间的关系图 1)3种算法的输出干噪比随着计算偏差角度的增大而增大,干扰抑制性能随之下降,由前面分析可知,当PI算法计算角度偏差为1°时,G-NW算法和G-NWD算法角度偏差分别为1.14°和1.28°。而从图4和式(24)中可以得出,当PI算法角度偏差为1°时只有29.38%的干扰被抑制掉,G-NW算法因增加了计算复杂度,即使在角度偏差为1.2°时,也能抑制67.78%的干扰,而G-NWD即使在角度偏差为1.4°时,也能有效抑制74.38%的干扰。 2)从图4可以看出,当角度偏差小于约0.5°时,G-NW算法的输出干噪比小于G-NWD算法的输出干噪比,说明角度偏差较小时,G-NW算法对干扰的抑制性能优于G-NWD算法。原因在于该仿真条件下,增加加深参数g的同时也增加了计算的复杂度,与零陷深度变浅的G-NW算法相比,耗费的时间代价更大;而当角度偏差大于该临界值时,因越来越偏离零陷中心最深的位置,导致G-NW算法性能下降,此时G-NWD算法因增加了零陷深度,即使干扰角度出现偏离,同样处于较深的零陷中。 综上分析,在高动态条件下,当零陷展宽参数一定时,且计算角度偏差大于某一临界点时,G-NWD算法能极大地提高G-NW算法的性能,反之,当计算角度偏差小于该临界点时,则无需采用以零陷加深为目的的G-NWD算法。 笔者针对零陷加宽方法导致深度不足、干扰抑制性能减弱的问题,提出了一种基于高斯分布的零陷展宽并加深的G-NWD抗干扰算法。首先根据特征子空间投影方法提取干扰分量,通过加权计算增加深零陷深度,构造新的协方差矩阵,利用功率倒置算法进行抗干扰。根据高动态环境,研究干扰扰动参数ξmax和加深参数g的取值以及计算角度偏差对G-NWD算法的影响。 仿真实验表明,在高动态条件下,干扰扰动参数ξmax和加深参数g的取值需要根据实际情况进行选择,ξmax取值过大或过小都会降低算法干扰抑制性能,而g值增大到一定数值后,算法的干扰抑制性能趋于稳定;当零陷展宽参数一定时,且计算角度偏差大于某一临界点时,G-NWD算法能极大地提高G-NW算法的性能。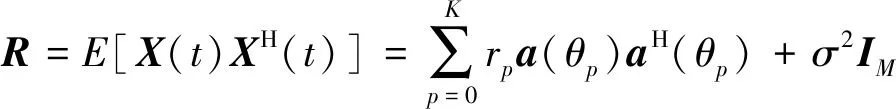
1.2 算法原理
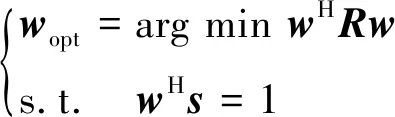







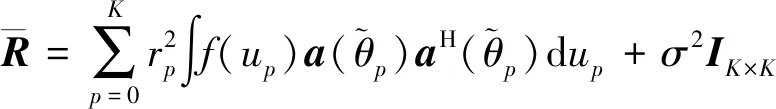
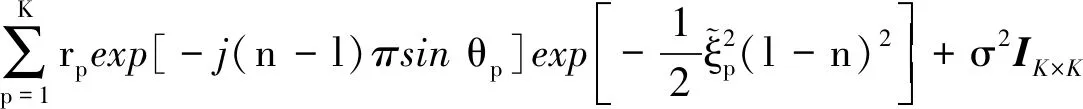








2 基于高斯分布的零陷展宽并加深(G-NWD)算法


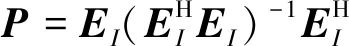



3 仿真实验
3.1 G-NWD算法性能分析

3.2 扰动参数对算法性能的影响

3.3 加深参数对算法性能的影响


3.4 计算角度偏差对算法性能的影响


4 结 语
