同心鼓运动模型的相关研究
2020-04-23王鑫张乐民王宁宇柳庆新
王鑫 张乐民 王宁宇 柳庆新*
(1.河海大学计算机与信息学院 江苏省南京市 211100 2.河海大学理学院 江苏省南京市 211100)
拓展项目“同心协力”需要参与者充分发挥团队协作能力。所用道具是一面双面鼓,鼓身固定多根绳子,绳子在鼓身上的固定点沿圆周均匀分布,每根绳子长度相同。团队成员每人牵拉一根绳子,尽量使鼓面保持水平。项目开始时,球从鼓面中心正上方竖直落下,队员协力拉动鼓将球颠起。
项目所用排球的质量为270g。鼓面直径40cm,鼓身高度为22cm,鼓的质量为3.6kg。队员人数不能少于8 人,且之间的最小距离不得小于60cm。项目开始时,球从鼓面中心上方40cm 处竖直落下,球被颠起的高度应离开鼓面40cm 以上。项目的目标是使得连续颠球的次数尽可能多。活动过程中队员只能抓握绳子的末端,不能接触鼓或绳子的其他位置。
根据题目所给条件,我们进行以下假设:每个队员的位置经安排后不再改变,在颠球过程中不会发生移动。球运动过程中按照理论规律运动,不存在其他外界因素(如风、空气阻力)的影响。鼓与球的材质均匀,可按一种材质计算,同时鼓内看作空心。第四问中“两位队员”指的是相邻的两位队员。鼓的转动过程与刚体转动过程类似。
1 问题一:理想状态下团队最佳协作的颠球高度
1.1 策略目标分析
影响人颠球次数直接影响因素为绳的拉力大小。设团队有n 个人,相邻两位队员之间的夹角为θ,绳上的拉力为Fh。
因为每个人都可以精确控制用力方向、时机和力度,则不妨设球与鼓运动状态稳定后,作用在鼓上的合力F1为大小恒定的力。在球与鼓两次相撞的中间时段,F1作用的时长为t'。为使鼓和球一起运动的系统耗能最小,颠球的高度Н 应尽量低。所以,Н=40cm。对于鼓球系统,所以,稳定后的鼓球系统,每一次球都应当在同样的位置发生撞击(假设发生撞击后立即相互脱离,两次撞击的时间间隔为一个周期时长T)。
1.2 球和鼓撞击状态分析
球由撞击点到最高点的距离与最高点到下一次撞击点的距离大小相等,均为Н,期间球只受重力作用。可求得T=0.5714s,撞击前排球的速度撞击后排球的速度(以竖直向下为正方向)。由动量守恒和非完全弹性碰撞规律,撞击前后状态可列(设鼓面材料为PVC):
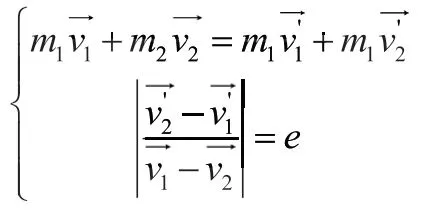
1.3 鼓的运动状态分析
撞击后立即撤销F1,在之后的某时间段t',以撞击瞬间为时间起点。在两次撞击过程中,鼓运动位移为0,同时满足动量守恒,可建立如下方程:
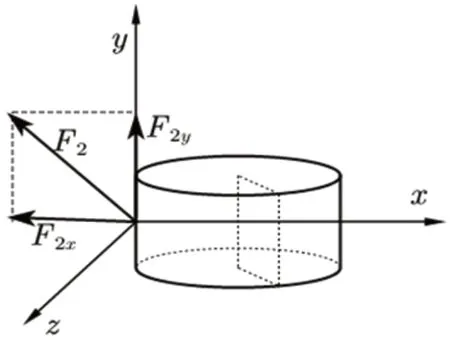
图1:F2 的分析图
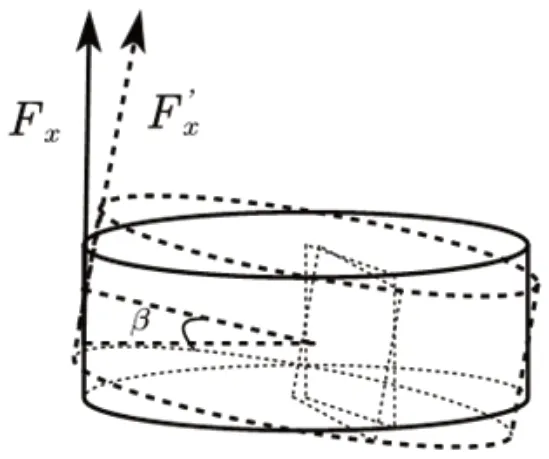
图2:鼓面转动示意图
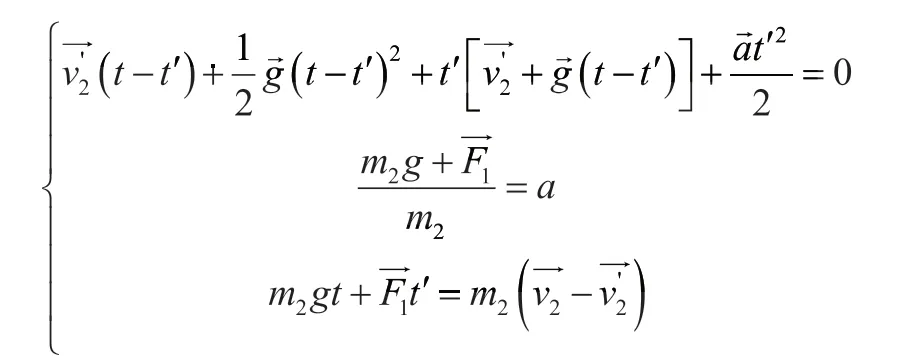
1.4 竖直方向合力F1与绳拉力Fh关系确定
假设已知人数n,则竖直方向合力F1在某一条绳上的分量为某一时刻绳与水平面的倾角φ,则为Fh在竖直方向分量大小,具体关系如下表示:
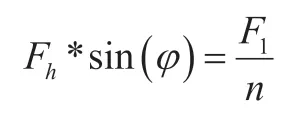
1.5 判断人数
设两人之间的距离固定为x,相邻两人之间夹角θ。由几何关系可确定人到鼓的水平距离为R。绳较初始位置下降距离h。由几何关系建立如下方程组:
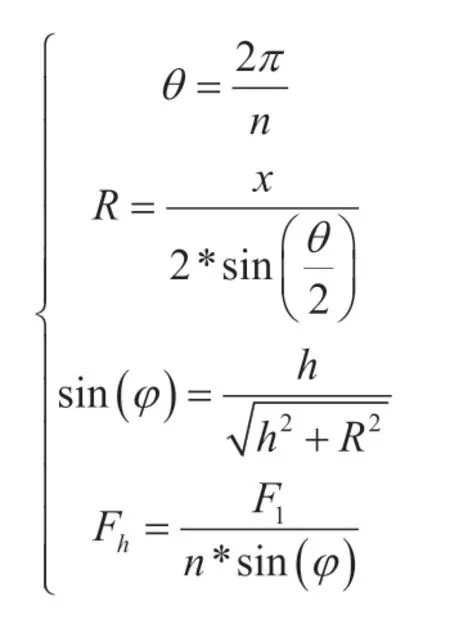
化简得n 与Fh之间的关系式:
最佳策略为一个团队8 个人,控制竖直方向合力大小41.013N,发力时机为撞击点后0.043s,发力时长为0.5214s。
2 问题二:球员失误操作的结果分析
2.1 某些球员用力过大
由于题目未给出队员的具体站位,我们默认八位队员相邻夹角相等,容易给出夹角该情况下每一位队员正对面均有另一位队员。
由于队员的手可以在一定范围内自由移动,可以假设绳子末端在队员所站位置上方。鼓的材质均匀且空心,可以由表面积比例关系给出鼓面的质量m1=1.7147kg,鼓身的质量m2=1.8853kg。
需要考虑多位队员在一个时间段内同时发力时,情况较为复杂,需要给出不同情况的受力分析。分析文下表1 数据可以得出结论,即同一时刻内只有三种发力的人数情况:1 人、2 人或8 人。下面根据同时间段内发力的人数分三种情况讨论。
2.1.1 情况1
在只有1 人发力时给出一个队员施加作用力F2的分析图1,由于这里鼓面发生转动的同时必定带动绳子移动(如图2),力的大小和方向都将随之改变,若要精确求解,需要给出两者的函数关系再进行积分,而两者的函数关系较复杂。实际上,由于转动的角度很小且力作用时间很短,可以认为在这段作用时间内绳子的位置不变,即可将力向量当作定值计算。
该力距竖直方向有一定的倾斜角为φ,根据刚体转动定理,F2在垂直此时鼓面(此时鼓面水平)的分量影响了鼓面的转动,而水平分量对转动不造成影响。鼓面发生一定的角度转动后,需要重新分解合力F2,产生新的影响转动的分量,但由于过于复杂且影响较小,这里同样不加入计算。
根据转动定理及角速度关系,可以给出0.1 秒后鼓面倾角β 的计算方程组。

2.1.2 情况2
在2 人同时发力时,可以再细分为两种情况讨论。即2.1 情况:两人夹角为180°,即刚好面对面站位,此时受力分析图如图3 所示。
根据上文单个力的作用假设,两个拉力向量在水平方向上的分解力不会影响转动,现在考虑其在竖直方向上的分力,假设其中一个分力为Fy1,另一个为Fy2,两者仅有两种可能关系:情况2.1.1:Fy1=Fy2;情况2.1.2:Fy1≠Fy2。两者相等时,其和力矩方向向上,使鼓发生竖直平动,此时不发生转动;两者不等时,力较大的那一方将使鼓转动,转动过程的解析类似情况一,不同的是,公式中的Fy需替换为Fy1-Fy2,即:
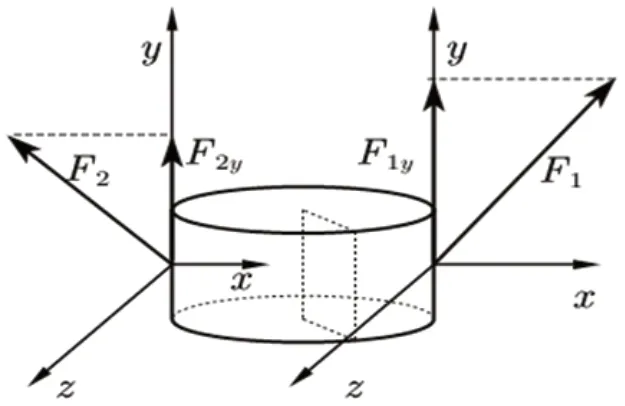
图3:两人夹角为180°时鼓的受力分析

图4:两人夹角小于180°的情况
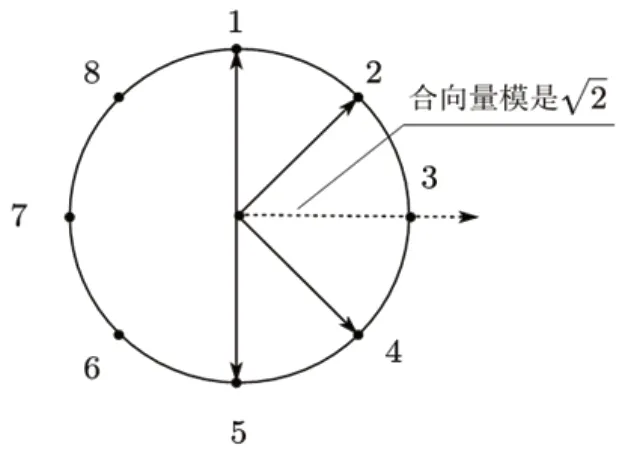
图5:第八组的pos 值合成
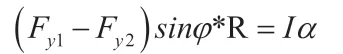
2.2 情况:两人夹角小于180°(如图4),此时较难确定鼓面的转轴,但是分析表1 数据可以看到,这种情况发生时,两个力的大小均相等,按照刚体转动规律,相等的两个力的力臂d 应当等长且平行,于是可以用直线l1连接两人并过质心做的平行线,即可得到该情况下的转轴。
2.1.3 情况3
八个人同时间段内发力时,由于两两对称,可以依据不同具体情况分解为情况一或情况二进行计算。
2.2 具体求解
考虑到9 组数据中每组数据在持续时间及发力大小上有许多不同,我们将其分为三种类型进行求解:1.每个队员发力时机均相同,但有个别队员用力大小不同(1、2、3 组);2.每个队员用力大小相同,但有个别队员发力时机不同(4、5、6 组);3.有个别队员或用力大小不同或发力时机不同(7、8、9 组)。这里约定:在同一时间段内站位刚好相对且用力大小相等的两位队员可根据模型二中的情况2.1.1 处理,即不将其加入对转动的影响因素中,下面的求解不再赘述此步骤。
2.2.1 类型一(1、2、3 组)的求解

表1:发力时机(单位:s)和用力大小(单位:N)取值

表 2:队员的评价数值
在这个类型中,队员发力的持续时间均只持续了0.1s 且在同一时间段内,只需合理应用模型二分析。第一组按情况2.1.1 谈论即可,囿于篇幅这里仅给出第二组的具体解法,第三组解法类似第二组。
第二组中仅需考虑四位队员:编号1、2、5、6,其中1 和5 相对,2 和6 相对,将相对的两位队员运用情况二Fy1≠Fy2时的结论,可将需要考虑的力减少到2 个即编号1、2 队员方向的力,再运用情况二的第二种细分情况即可。
2.2.2 类型二(4、5、6 组)的求解
分两段时间考虑,第一段0.1s 内作用力将使得鼓产生一定的角加速度,在第二段0.1s 内由于用力大小均相同,鼓不再具有角加速度,即做匀速转动。第4 组在第一段时间中运用情况2.1.2 算出角加速度α 后可以给出第一段0.1s 末的角速度计算式:

从而鼓面的总倾角:
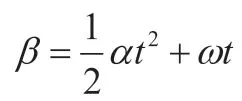
第五、第六组解法与其类似,不同的地方在于第一段0.1s 中需运用两次情况2.1.2 再运用情况2.2 才能得到角加速度α。
2.2.3 类型三(7、8、9 组)的求解
与类型二相比,类型三两段时间均有角加速度,且这两段时间内的角加速度方向大小均不相同。还是同样的方法给出第一段时间及第二段时间内的角加速度α1、α2,这时鼓面在两端时间内有不同的转轴,因此将运动分解为两个方向,分别用两个角加速度算出合空间角,以鼓质心为坐标原点建立空间坐标系,假定第一段时间内鼓面转轴为y 轴,则可以由几何关系给出第二段时间内转轴方向,从而给出具体角度值。第8 组绕第一转轴转动的角度为β1,绕第二转轴转动角度为β2,求得法向量加和在空间坐标系中几何求解可得鼓面倾角。
用上述方法求得所有实验组数据如表1 所示。
3 球员失误影响分析即最佳策略的调整
3.1 数据处理
先约定名词定义,把每一组实验中发力时机为-0.1s 的数据称作一型失误;用力大小为90 的数据称作二型失误;从“1、2 人分解”模型中得到启发,在多人不同时不同力度发力时,最终决定鼓面倾角的仅与失误直接相关而与其他正常数据几乎无关,从而提出描述失误数据站位的影响程度。
将问题二中的数据看作9 组相互独立的实验,与现实情况相同,其失误发生的概率均满足随机性。
可以看出其中的自变量:一型失误影响程度Tf、二型失误影响程度Fn和失误数据站位的影响程度pos 都与鼓面倾角的数值β 有不同程度的相关性,即可以表示为若想给出具体的相关程度,需要给出每组实验中三个影响因素对应的唯一数值。
考虑一型失误影响程度Tf。每位队员的发力时机tf只存在提前发力或正常时机发力两种情况,用0、1 表示,即:

一组实验内的发力时机程度值Wf可通过各个队员的wf值累加求和得到,即:
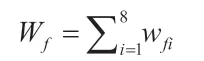
考虑二型失误的影响程度Fn,Fn取该组实验中不正常力度出现的个数。
考虑失误数据站位的影响程度pos。这里的“失误”需要综合考虑一型失误和二型失误,虽然现在我们还不能拿到数值来准确描述这两类型失误的影响程度,但可以明确的是:同一位队员在一次实验中发生失误的次数越多影响肯定更大。
即,可以将在一次实验中某一位置的队员发生失误的次数取做该站位的pos 的数值,而pos 的方向与沿方位的绳向外。整体的pos 值由各个站位的pos 值向量合成得出。

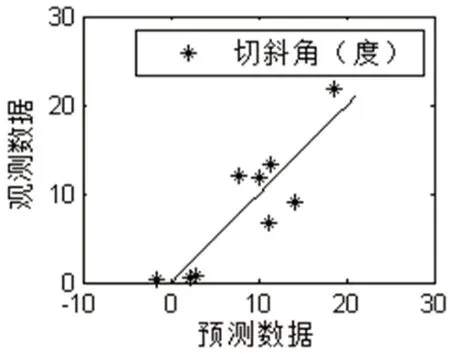
图6:样本点绘制预测图
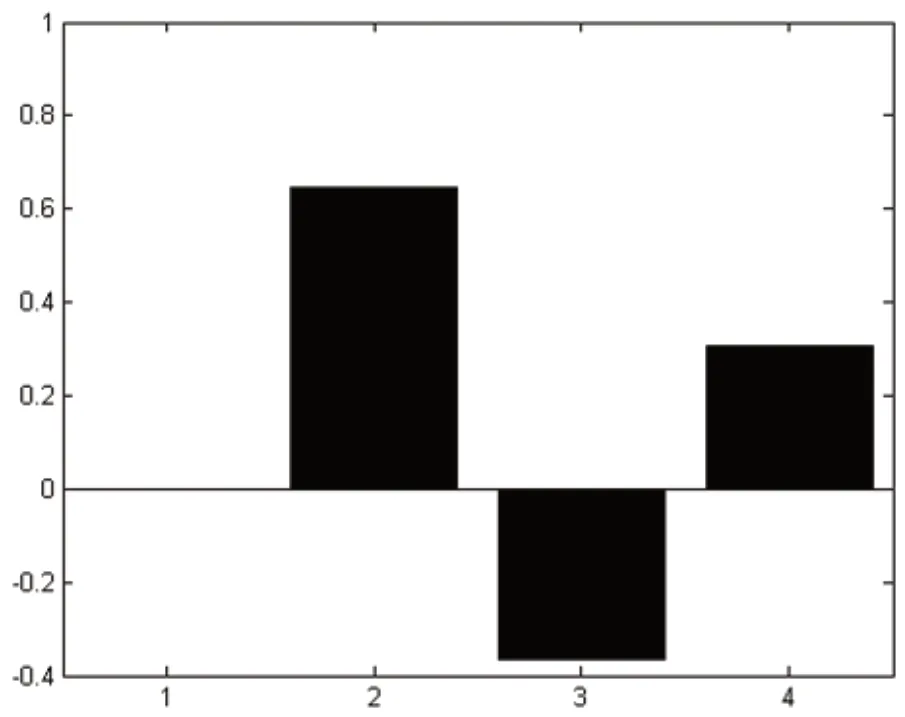
图7:回归系数的直方图
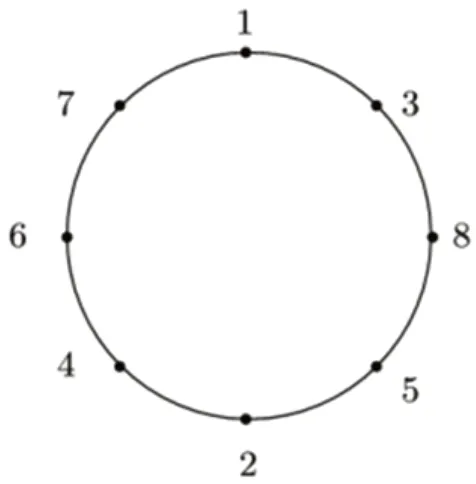
图8:P 值最小时的站位情况
以第八组实验为例,如图5 所示。
接下来用上述体系求出9 组实验的Tf、Fn、pos 值与鼓面倾角值β 拟合函数。由于三中因素量纲不同,先对这三种数据用zscore函数进行无量纲标准化。
Matlab 中输入偏最小而成回归命令plsregress 拟合处理后的数据,得到标准化指标变量之间的回归方程:

为考察拟合效果,我们以观测数据和预测数据对所有的样本点绘制预测图如图6 所示,可以看出函数拟合较好。
分析回归系数的直方图7,一型失误影响程度较大,二型失误的影响程度和失误数据站位的影响程度相当,其中二型失误与鼓面倾角为负相关关系。
在9 组实验中,参与的队员相同且他们的站位始终不变,即某一方位的数据全是来自于同一队员的,据此我们可以通过这9 组数据确定各个队员的能力评价数值,该过程我们使用了Topsis,即优劣解距离法。
现在有8 个要评价的对象,2 个评价指标(发力时机失误及用力大小失误)的标准化矩阵:
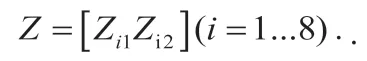
定义最大值Z+
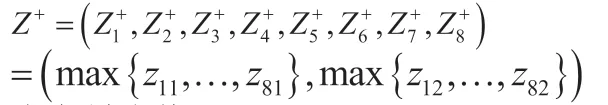
定义最小值Z-

定义第i(i=1,2,...,8)个评价对象与最大值的距离
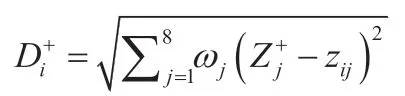
定义第i(i=1,2,...,8)个评价对象与最小值的距离
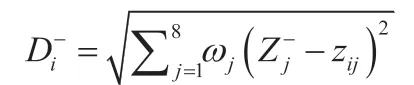
那么,我们可以计算得出第i(i=1,2,...,8)个评价对象未归一化的得分:很明显且Si越大 越小,即接近最大值。算得各队员的评价数值pi见表2。
在本例中,某名队员的评价数值代表了其操作过程中的不稳定性,数值越高越不稳定越容易出现失误。
3.2 站位策略调整
每个队员的操作稳定性是其自身属性,不能再做出更改,在给定一组特定的队员后若想使得失误发生时的鼓面倾角尽可能小,唯一能调整的是该组队员的站位,通过站位的调整降低失误带来的影响。
仿照计算pos 时的方法,将一种站位策略形成的总操作稳定性P 定义为各个队员评价数值的矢量累加,即目标函数为min(P),即在所有可能的站位策略中求出总操作稳定性最强的策略。以表1 的9 组实验数据为例,用C++循环求解8 位队员的中站位可能,得到P 最小值为0.1619,该策略的站位安排如下图所示,其中3、6、7 号位由于稳定性相等可以互换位置,对结果不影响。可以认为该策略最大程度上使得队员操作的稳定性最强如图8。
