基于多重递阶结构的无人直升机航线控制
2020-04-23戴勇
戴勇
(南京模拟技术研究所 江苏省南京市 210016)
1 引言
无人直升机是一种可人工远程操纵,进行超视距飞行的非载人飞行器,能够执行电力巡线、测量测绘、侦查打击等多种任务,在民用及军用领域有着广泛的应用[1]。当前,世界各国争相发展无人机技术,代表型号有美国的火力侦察兵、奥地利的S-100 等[2]。这些无人直升机能够按预设航线飞行,在无人操作的情况下完成恶劣环境(尤其是强风、高温等环境)的飞行任务。
航线飞行是无人直升机完成任务不可或缺的关键功能。传统无人直升机的航线控制采用了航迹角控制器和航线侧偏距控制器的并联设计方法,该方法在特定情况下容易产生航线侧偏距稳态偏差问题。针对传统方法存在的问题,根据大系统理论多重递阶控制思想
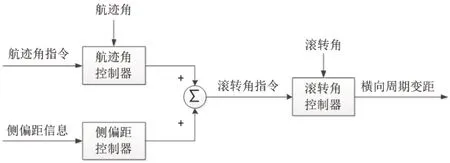
图1:侧偏距控制结构图
[3],本文提出了基于多重递阶控制结构的航线侧偏距控制方法。该方法将航线飞行控制系统划分为三个回路,外回路通过控制解算将航线侧偏距信息转化为期望的航迹角指令,中回路将航迹角指令转化为期望的滚转角指令,内回路实现滚转角指令的跟随控制,从原理上解决了传统方法的侧偏距稳态偏差问题。在半物理仿真系统中,将两种方法进行了对比仿真,结果表明,本方法有效改善了无人直升机的航线飞行性能,航线飞行侧偏距控制效果良好。

图2:基于多重递阶结构的无人直升机航线控制原理
2 航线控制并联设计存在的问题
传统的航线飞行控制算法,主要由航迹通道及横向通道的操纵实现[4]。现主流控制算法采用并联式控制结构设计,侧偏距主要以尾桨距起阻尼和协调作用,以滚转运动进行航迹控制[5]。
航线控制并联设计算法如下:
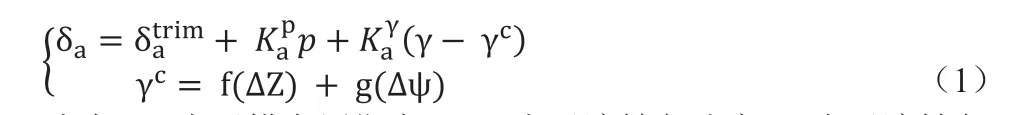
式中,δa表示横向周期变距,p 表示滚转角速度,γ 表示滚转角, γc表示滚转角指令,ΔZ 表示侧偏距,Δψ 表示航迹角偏差,f(.)、g(.)分别表示侧偏距控制律和协调转弯控制律。
该算法利用了航迹角对无人直升机的滚转通道交叉补偿,其控制结构如图1 所示。
如图1 所示,该控制结构采用双控制器并联控制的方式完成飞行航线侧偏距的实时修正,其核心思想在于:协调转弯控制器与侧偏距控制器合成滚转角指令,进而控制无人直升机实现航线飞行。并联式控制结构简单,但是物理概念不明确,容易出现两个控制器输出指令冲突的现象,产生零和效应,进而导致飞行航线的侧偏距出现稳态偏差。
以经典控制方法为例,进一步说明该问题。如果侧偏距控制器和协调转弯控制器均存在积分控制环节,在航线飞行过程中,很容易出现侧偏距积分器与航迹角积分器反向对消的现象,最终导致两路控制器的滚转角指令出现零和效应,使无人直升机出现稳态的侧偏距偏差,严重影响航线控制精度。
3 基于多重递阶结构的航线控制方法
为克服传统方法带来的问题,进一步提高航线飞行的控制精度,本文提出了基于多重递阶控制结构的航线飞行控制算法。
多重递阶控制思想指出:根据大系统的自然属性,可将复杂问题分解成若干相互独立的子问题,通过子问题的协调配合实现系统最终目标[3]。受此观点启发,将航线控制系统划由外而内划分成以下三个回路:
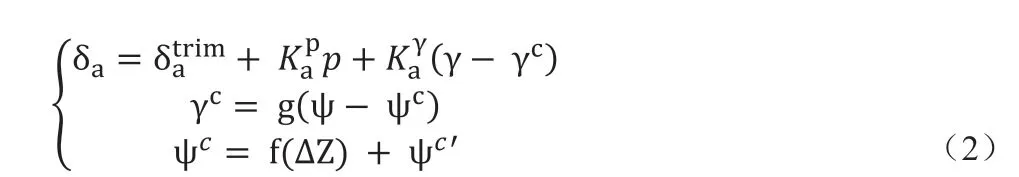
式中,δa表示横向周期变距,p 表示滚转角速度,γ 表示滚转
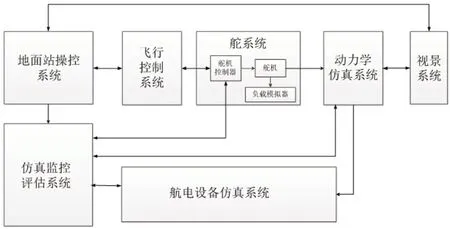
图3:无人直升机半物理仿真系统组成

图4:无人直升机偏航角响应曲线图
(1)外回路为航迹角指向回路,通过控制解算将航线侧偏距信息转化为期望的航迹角指令;
(2)中回路为协调控制回路,通过控制解算将航迹角指令转化为期望的滚转角指令;
(3)内回路为姿态跟随回路,实现滚转姿态指令的跟踪控制。
三个回路的物理概念清晰明确,且三个回路之间是简单串联关系,从原理上避免了并联控制带来的控制冲突问题,从而解决传统方法的侧偏距稳态偏差问题。
本算法的控制结构如图2 所示。
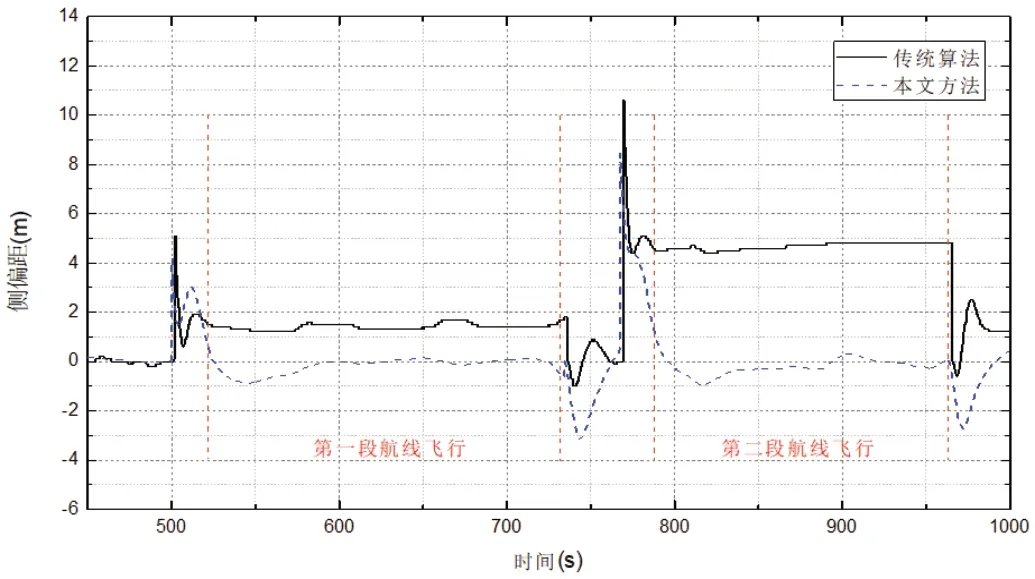
图5:无人直升机侧偏距响应曲线图
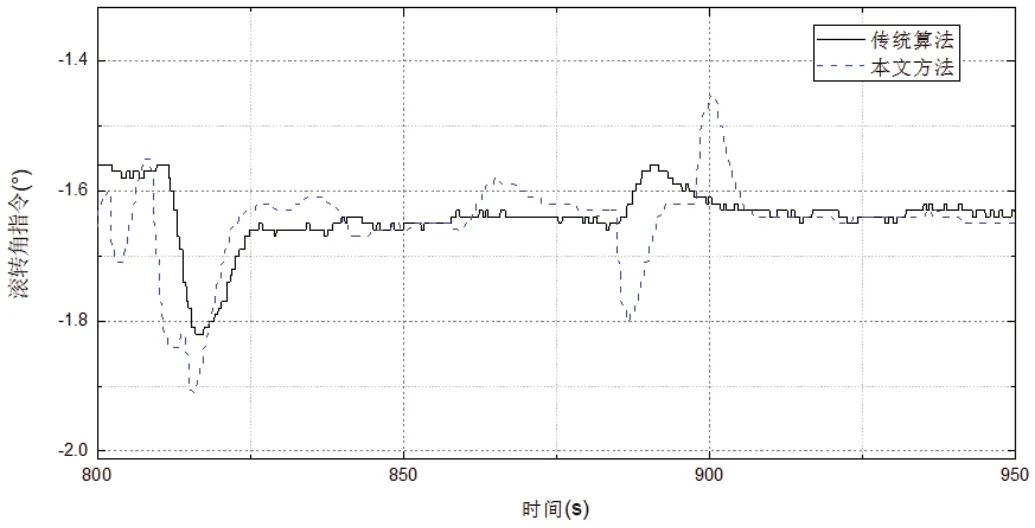
图6:无人直升机滚转角指令曲线图

图7:无人直升机偏航角指令曲线图
基于多重递阶控制结构的航线飞行控制算法如下:角,γc表示滚转角指令,ψ 表示航迹角信息;ψc表示航迹角指令,ψc'表示航线方向,ΔZ 表示侧偏距;g(.)表示协调控制回路的控制律,f(.)表示航迹角指向回路的控制律。
4 仿真结果与分析
为验证本文方法的有效性,本文利用研究所的无人直升机半物理仿真系统,开展两种方法的对比仿真试验工作。无人直升机半物理仿真系统组成如图3 所示,其中,某型无人直升机动力学仿真系统采用了先进的飞行器飞行仿真与工程分析软件Flightlab 进行构建。
仿真过程中,采用两种控制算法分别在同一条航线上飞行的方式进行。图4 为无人直升机飞行过程中的偏航角响应曲线,由图可知,整个模拟架次进行了两个航线段的飞行,其中520 秒至730 秒进行第一段航线飞行,前飞速度为23 米/秒;520 秒至780 秒以盘旋方式进行航线切换,无人直升机的前飞速度为23 米/秒;780 秒至960 秒进行第二段航线飞行,前飞速度为25 米/秒。
图5 为航线飞行侧偏距的响应曲线,由图可知,并联式控制算法在第二段航线飞行时出现了零和效应,始终维持在5 米左右。本文方法在两段航线飞行中侧偏距都在0 米附近,体现出更好的航线跟踪性能。
图6、图7 展现了第二段航线飞行时滚转姿态和偏航角动态响应细节,由图可见,在800 秒至950 秒进行的第二段航线飞行时,并联控制算法则产生了5 米左右的侧偏距稳态误差,而此时的滚转角指令与航迹角指令都维持不变,导致控制器并没有输出相应的控制动作,这是零和效应的具体表现。
由此可见,采用本文方法的控制效果要明显好于传统算法,传统算法在特定情况出现了侧偏距的稳态偏差,本文方法在航线飞行全过程中始终能够较好地修正侧偏距误差,稳态航线侧偏距控制在±1 米以内,取得了理想的控制效果。
5 结论
本文针对传统方法存在的稳态偏差问题,分析了问题产生的原因,根据大系统多重递阶的控制思想,提出了基于多重递阶控制结构的航线飞行控制方法,从原理上解决了传统方法带来的侧偏距稳态偏差问题。在半物理仿真系统中,对两种方法进行了对比仿真测试。结果表明,本方法改善了无人直升机的航线飞行性能,有效解决了侧偏距稳态偏差的问题,为无人直升机执行高精度的航线飞行任务奠定了技术基础。
