基于单张图像重建的孔洞修补研究

刘畅

摘要：在通过PSGN网络得到单张图像生成的三维点云后，由于点云精度较为稀疏，因此在表面重建后含有孔洞。提出使用隐式拟合方式进行表面重建后，針对模型有孔洞的情况，找出孔洞进行网格三角化、网格细分、网格平滑，最终得出完整封闭的几何体模型。

关键词：点云;泊松方程;孔洞修补;深度学习;三角剖分

中图分类号：TP393 文献标识码：A

文章编号：1009-3044（2020）06-0185-02

1概述

随着深度学习研究越来越受到学者欢迎，无论是人脸识别还是无人驾驶的新闻都更多出现在大众的视野，所以研究者们也将目光投入了三维重建技术与深度学习的结合。早年三维重建多是以序列图像或是双目、单目采集到的视觉图像作为数据进行研究，但如今使用单张图像也可以进行三维重建。很多人或许提出这样的疑问，一张图像所得到的数据如此少，怎样才能进行三维重建？这个问题在深度学习快速发展以后得到了很好的回答。

常见的三维重建表现模式分为四种：深度图、体素、点云、网格。针对单张图像三维重建并且结合深度学习进行研究的进程中，基于体素重建的典型网络结构为3D-R2N2，该网络结合GRU和LSTM的思想构建了单视图与多视图相结合的体系，缺点在于会随着模型精度增高计算量会得到指数级的增长;基于点云重建的典型网络为PSGN，该网络结合卷积与反卷积层进行特征提取，联合两个分支得到最后的点云数目，一个分支预测全局点云，一个分支预测局部点云;基于网格重建的典型网络Pixel2Mesh，该网络一部分提取图像特征，一部分利用变形思想，以三维椭圆网格作为三维重构目标的初始化结构，将图像的浅层到深层的特征，反映到三维椭圆网格形状的改变上。这些网络的出现使得单张图片重建在各种表现形式上都显示出非常不错的结果，后续也有很多学者在这几种网络上进行改进，并且也进一步得到良好效果。

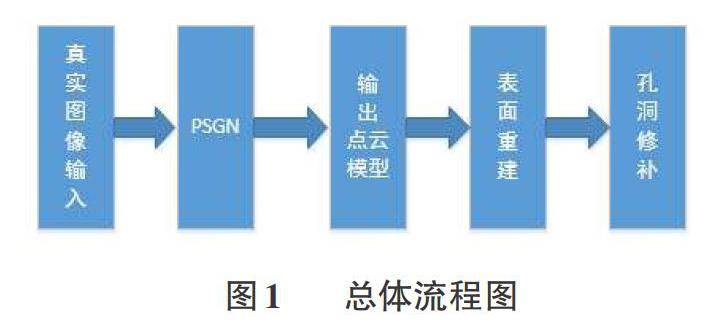
2总体流程

本文总体流程为首先拍摄现实岩石图像作为PSGN数据，得出数量为1024的点云三维模型，第二步经过泊松表面重建得到初步的表面模型图，第三步针对模型具有孔洞的地方进行修补。该算法在windows系统上完成，运行平台为VS2013，所使用到的开源库有PCLl.8、BOOSTl.61.0、CGAIA.9、Open-Mesh5.1。

2.1单张图片三维点云模型重建

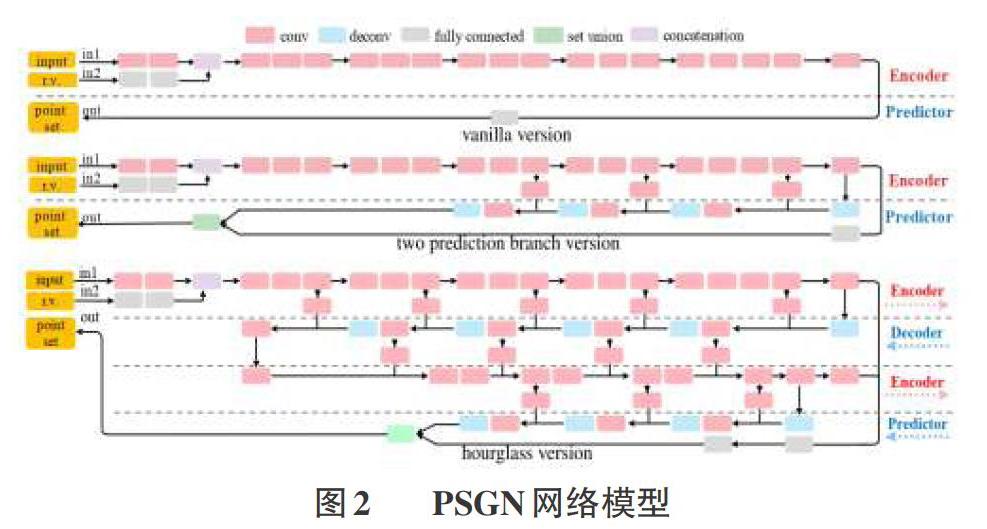
2016年Fan提出的PSGN网络含有两个分支，其一卷积层和反卷积层形成最终点云的整体结构，其二全连接层加强局部点云的生成。本次实验使用的版本为hourglass version，类似于漏斗类型，改版本中加入递归循环能够更好地进行编码解码，综合全局以及局部的信息，特别是在需要在局部进行表现的区域，该网络可以得到效果不错的表现。

2.2表面重建

生成点云的三维模型以后，本文选择使用网格形式进行表现。选择使用三角网格形式原因是易于生成，并且在进行进一步操作时，三角网格相比于多边形网格具有更多成熟的算法可以供使用。

本文选择泊松重建，泊松重建的步骤：

①求解泊松方程取得点云模型表面的信息。

②利用获取到的隐形方程进行等值面的提取。设置变量值为j，当j>0时则设定在模型内部;当j<0，则设定在模型外部，只提取j=0的等值面。

③根据等值面提取得到具有真实几何实体表面信息并得到模型。

2.3孔洞修补

孔洞修补[6]首先需要找到属于孔洞的边界，再针对孔洞进行三角剖分。如果该条边属于孔洞的边，那么该条边一定只有一个三角片与之相连，我们可以利用这一特性进行寻找孔洞的边界。

在寻找开始之前，应设置结构存储顶点v、边h以及面f，根据孔洞特性进行寻找模型中缺失的位置具体分布在哪里，找出具体位置进行存储并进行填充。填充孔后，根据CGAL库的使用说明，可以使用节网格划分中描述的网格划分函数cgal：：polygon_mesh_processing：：refineO和cgal：：polygon_mesh_pro-cessing：：fair（）对生成的面片进行细化和光顺。

3实验结果

3.1点云模型的生成

输入单张真实岩石图片（如图3所示），岩石种类选择没有限制，可以是砂岩、石英岩，也可以是玄武岩。岩石不同于ShapeNet数据集中常见的飞机、椅子等模型，得到点云模型（如图4所示）的结果同样也显示出该网络也较好的可扩展性。由图3和图4可见，图3左起第一张原始图对应图4左起第一张点云模型图，其他图片同理。

3.2泊松表面重建

在点云文件生成后，下一步进行表面重建。在表面重建中使用滤波进行图像处理，使用低通滤波，即阻高频通低频使得图像进行平滑。随后进行法向量的计算，设置搜索树搜索半径为5，将点云数据的坐标和法向信息拼接，随后开始泊松重建，并保存为ply格式。如图5所示，依次为原始图像，经过PSGN网络形成的点云模型，再经过泊松重建后的表面非封闭几何模型。由于PSGN网络输出点云个数仅仅只为1024个，因此在表面重建后会形成非封闭的表面模型，所以为形成封闭几何体，就要进行缺失的孔洞修补。

3.3孔洞修补

将获取到的模型进行观察，发现模型两侧具有较大的孔洞，但岩石表面应是封闭几何体，因此必须进行空洞修补，才能得到较符合实际情况的模型。如图6所示，左起为含有孔洞的岩石表面模型，右边为经过修补后构成的网格模型，可以看到结果是完整的。

4结论

由实验结果可以表明，在针对具有孑L洞的表面模型中，利用网格的半边数据结构，结合孔洞结构特性进行修补，得到了不错的效果。在以后的研究中，还可以继续增加由深度学习网络得到的点云模型精度来进行表面重建，也可以得到较为完整的表面模型，在这一点上也是值得研究的领域。