海洋平台升降装置的齿轮齿条均载特性研究

2020-04-22陈宝庆叶福民孟淼

机械制造与自动化 2020年1期

陈宝庆，叶福民，孟淼

(江苏科技大学机械工程学院,江苏镇江212003)

0 引言

自升式海洋平台具有造价低、定位能力强、同步性好和用钢量少等优点，被广泛运用于海洋石油的开发和勘探工程[1]。齿轮齿条升降系统是自升式海洋平台的核心装置之一，其原理是通过一系列的减速变速过程，最终通过两个小齿轮与作为桩腿齿条的异侧啮合来提升平台。在理想状态下，齿条两侧的小齿轮受力是相等的。但是由于升降装置的振动、齿轮啮合误差等因素的影响，齿条和两侧小齿轮的啮合力存在一定的偏差，结果会造成升降装置载荷分布不均匀，即不均载的现象。这将会使平台产生振动、噪声，轮齿出现点蚀，甚至导致轮齿折断。

国内外学者针对齿轮的均载特性做了大量的研究，且现有的关于齿轮均载性能的研究，大都是针对行星轮系的均载性能研究。KAHRAMAN[2]建立了单级行星轮系的集中参数模型，并讨论了系统的固有特性。BODAS[3]等分析了载荷和轮齿制造误差对行星传动均载特性的影响; SINGH[4]等通过实验详细研究了行星传动系统中的载荷不均等特性;陆俊华[5]等人从动力学角度建立2K-H型行星传动系统的计算模型，研究了太阳轮浮动、装配和安装误差以及转速等因素对系统均载特性的影响。孙智民[6]等建立了行星齿轮传动系统非线性动力学模型，分析了齿轮副的综合误差和齿侧间隙对均载性能的影响; 方宗德[7]等得到了2K-H行星减速传动系统的时域和频域解，分析了各行星轮上的均载特性和轮齿偏心误差对其均载特性的影响;叶福民[8]等人建立了非等模数、非等压力角NGW 型行星齿轮系的计算模型，并通过建立方程，用理论推导的方式讨论了压力角、齿轮误差、啮合刚度等对系统的均载特性的影响。其他学者[9-10]也对多级行星齿轮传动系统的均载特性做了研究。

本文以自升式海洋平台齿轮齿条升降装置的桩腿为研究对象，分别从升降装置在载荷、压力角以及模数变化情况下，对齿轮齿条升降装置进行动力学研究，揭示升降载荷、压力角和模数对于均载系数变化的影响，可以为升降装置的设计优化提供理论参考，也可以为自升式海洋平台齿轮齿条升降装置动力学分析提供理论参考。

1 齿轮齿条升降装置的均载机构及系统的主要参数

图1为自升式海洋平台升降系统的示意图。电动机提供的动力传递给行星减速器的“中心太阳轮”，然后由行星架10和外齿轮1分别在左右两轴主动输出。2个主动七齿小齿轮构成一个“统一输出”的差动轮系，即2个左右七齿小齿轮的模数相同、转速相等。

升降平台在上下运动的过程中，小齿轮要承担平台的重力。在正常的工况下，每个升降单元的承载能力不能低于400t，所以每个小齿轮的承载能力为200t[11]。此升降装置是由6个小齿轮与一条齿条组成，因此给齿条质心加一个12000kN的力来模拟升降平台的载荷，研究对象是每根桩腿的升降装置的一组升降单元中的七齿小齿轮。表1为升降装置各部件参数。

1—外齿轮；2—七齿齿轮；3—齿条；4—七齿齿轮；5—带外圈的内齿圈；6—行星轮；7—太阳轮；8—惰轮；9—系杆；10—行星架。图1 海洋平台齿轮齿条式升降装置示意图

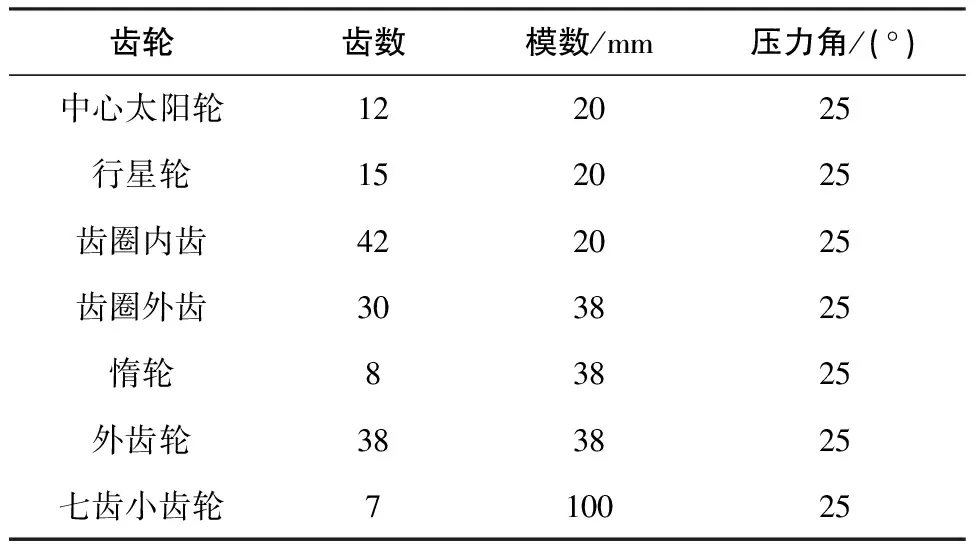
表1 升降装置各个部件参数

2 齿轮齿条升降装置动力学模型的建立

a) 升降装置的动力学模型

首先在Pro/E中建立升降装置的三维模型，接着在Pro/E中转换成Parasolid 格式中性文件，然后在ADAMS软件中导入中性文件，并对各个部件施加相应的约束、创建接触力并设置相应的参数，施加驱动。

b) 升降装置动力学模型的参数设置

1)约束的设置

与大地间建立旋转副的齿轮有：太阳轮、行星轮、小齿轮、外齿轮、齿圈，旋转中心为各自的质心；其中3个行星齿轮与大地之间建立旋转副时，小齿轮为参照物；齿条与大地之间建立移动副。

2) 接触力中参数的设置

接触刚度为2个物体接触时表面抵抗弹性变形的能力。根据赫兹理论，接触刚度系数计算如下：

(1)

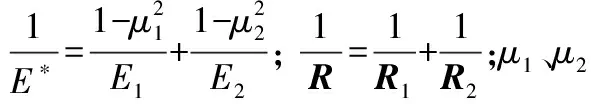
代入数据，得到刚度系数为3.98×106N/mm2。

3) 模型驱动的设置

由于太阳轮为输入动力的一端，因此给太阳轮施加驱动。设置转速为180°/s(30r/min)。求解器的仿真时间设置为t=20s，仿真步数stepsize=100。

c) 升降装置的动力学计算结果

当装置在正常升降时，平台承受的设计升降载荷为12000kN。得到齿轮齿条接触力曲线图，如图2所示。当小齿轮的升降载荷为12000kN时，每个小齿轮受到的切向力理论值FX为2000kN，那么小齿轮受到的接触力的理论值F0为:

(2)

式中：α为压力角，∂=25°，经过计算F0约为2200kN。

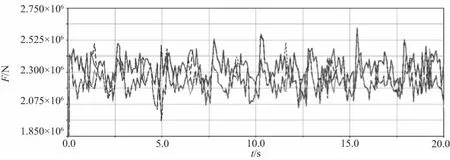
图2 载荷为12000kN时的接触力曲线图

3 参数影响分析

3.1 齿轮齿条升降装置的均载定义与计算

通过ADAMS进行仿真分析，在后处理中得到接触力的数值，导入到Excel中进行数据处理，再将数据导入到MATLAB中进行数据处理，得到均载系数随着升降载荷、小齿轮压力角、模数变化的曲线图。图3为齿轮齿条示意图，假设小齿轮1受到的载荷值为F1，小齿轮2受到的载荷值为F2，设小齿轮1和2受到载荷的理论值为F，设均载系数为β，小齿轮的均载系数为：

(3)

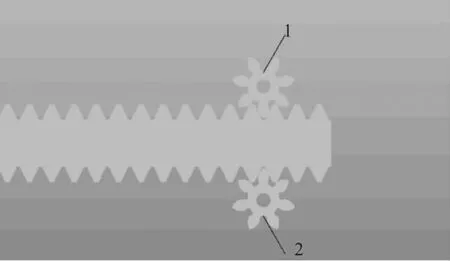
图3 齿轮齿条示意图

在ADAMS的PostProcessor模块中，得到仿真后曲线的参数，通过处理将数据导入到表格中，在表格中进行数值运算。由于齿条同一侧有3个小齿轮，所以每组只要测量1个，本文取后处理中的contact1和contact4曲线。通过Excel中的数值运算，得到均载系数，最后在MATLAB中绘制均载系数曲线。

由于最终得到的均载系数是一条曲线，为了便于比较，所以取曲线上最大值点作为小齿轮最终的均载系数。

3.2 载荷对于均载系数的影响

采用上述方法分别计算升降平台在载荷分别为18000kN、24000kN、30000kN，36000kN时的均载系数。在MATLAB中，通过输入代码得到曲线图，得到在不同升降载荷下，均载系数随着时间的变化曲线图一，如图4所示，同时得到均载系数随着载荷变化的曲线，如图5所示。

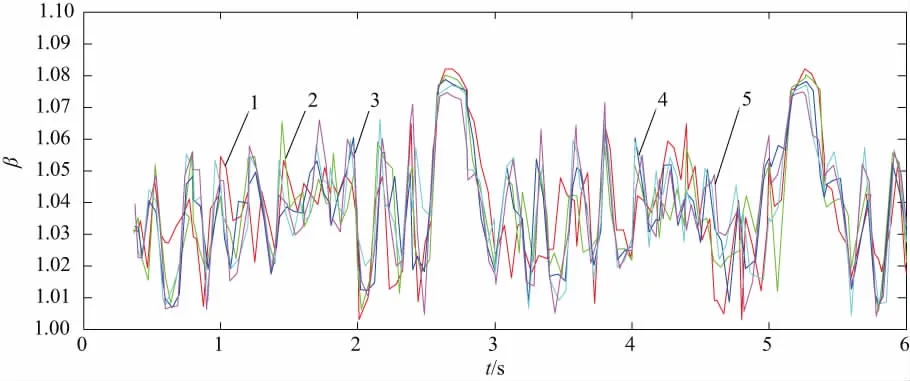
曲线1—载荷为12 000 kN时；曲线2—载荷为18 000 kN时；曲线3—载荷为24 000 kN时；曲线4—载荷为30 000 kN时；曲线5—载荷为36 000 kN时。图4 均载系数随着时间的变化曲线图一

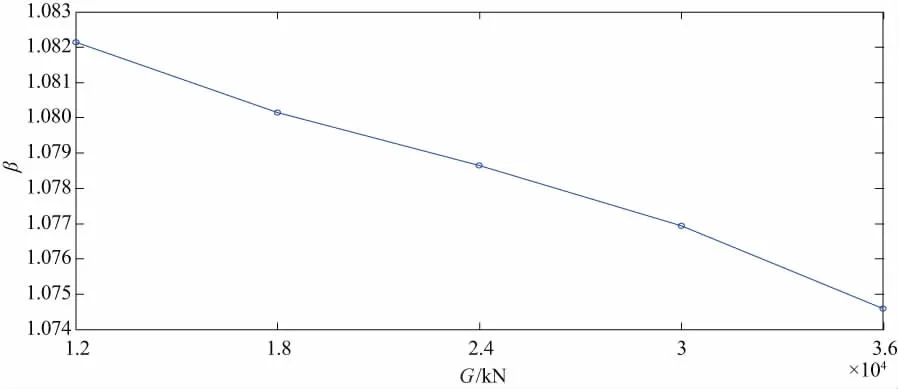
图5 均载系数随着载荷的变化曲线图

由图5可知，曲线有周期性的变化，周期大约为2.5s，这说明小齿轮转过一个齿大约需要2.5s。从图5中还可以发现齿轮发生了单双齿交替时，均载系数是明显变化的，双齿啮合的时候，均载系数大；单齿啮合的时候，均载系数小。由图6可以看出，小齿轮的载荷在增大的情况下，小齿轮的均载系数呈现出变小的趋势，均载系数的值大致在1.074～1.082之间变化。

3.3 小齿轮压力角对于均载系数的影响

分别计算小齿轮在压力角为25°、26°、27°、28°、29°时小齿轮的均载系数，得到在不同压力角下，均载系数随着时间的变化曲线图二，如图6所示，同时得到均载系数随着压力角变化的曲线，如图7所示。

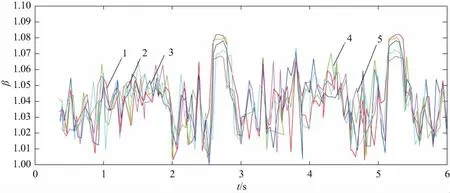
曲线1—压力角为25°时；曲线2—压力角为26°时；曲线3—压力角为27°时；曲线4—压力角为28°时；曲线5—压力角为29°时。图6 均载系数随着时间的变化曲线图二

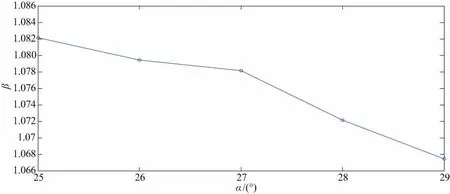
图7 均载系数随着压力角的变化曲线图

由图6可知，曲线有周期性的变化，周期大约为2.5s。这说明小齿轮转过一个齿大约需要2.5s。从图中可以看出，齿轮在运动过程中，均载系数是不断变化的，双齿啮合的时候，均载系数大；单齿啮合的时候，均载系数小。由图7可知，小齿轮在压力角变化的情况下，小齿轮的均载系数大致在1.067～1.082之间变化，而且随着小齿轮压力角变大，均载系数呈现变小的趋势。

3.4 小齿轮模数对于均载系数的影响

分别计算小齿轮的模数为90mm、95mm、100mm、105mm、110mm时小齿轮的均载系数，得到在不同模数下，均载系数随着时间的变化曲线图三，如图8所示，同时得到均载系数随着模数变化的曲线，如图9所示。

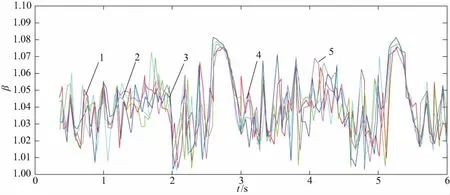
曲线1—小齿轮模数为90 mm时；曲线2—小齿轮模数为95 mm；曲线3—小齿轮模数为100 mm时；曲线4—小齿轮模数为105 mm时；曲线5—小齿轮模数为110 mm时。图8 均载系数随着时间的变化曲线图三

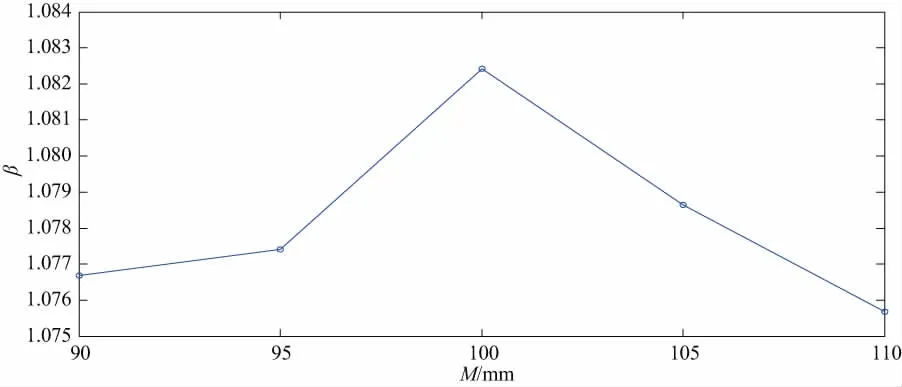
图9 均载系数随着模数的变化曲线图

由图9可知，曲线有周期性的变化，周期大约为2.5s，这说明小齿轮转过一个齿大约需要2.5s。由图10可知，当小齿轮模数由90mm变化到110mm时，小齿轮的均载系数呈现先增加后减小的趋势，即小齿轮的模数在从90mm增加到100mm的过程中，均载系数是变大的，而小齿轮的模数在由100mm增加到110mm的过程中的时候，小齿轮的均载系数呈现变小的趋势。