基于等效刚度的输电杆塔简化方法
2020-04-22叶中飞陶亚光宋高丽任鹏亮
伍 川, 叶中飞, 陶亚光, 张 博, 潘 勇, 宋高丽, 任鹏亮
(国网河南省电力公司电力科学研究院,国网输电线路舞动防治技术重点实验室,郑州 450052)
近年来,因输电线路舞动、脱冰跳跃导致的金具破坏、断线、闪络和倒塔等事故时有发生,严重影响线路的安全运行。快速明确复杂动载条件下线路破坏原因,对于线路改进、保证线路安全运行意义重大。而输电杆塔作为典型的桁架结构是线路结构中最为复杂的组成部分。因此,如何快速实现杆塔的简化分析将是快速实现线路塔线体系分析的关键。
目前输电杆塔数值分析方法主要包括实体建模分析方法[1-2]、杆梁混合模型简化分析方法[3-15]、挂点固定约束方法[16-20]三大类。刘力宇[1]和吴天宝等[2]采用局部三维实体精细化模型研究了杆塔在脱冰等复杂工况下的受力特性,分析了螺栓滑移过程等对杆塔的影响。Kitipornchai等[3]、齐立忠等[4]、高康等[5]、江文强[6]以空间杆梁模型为基础,在杆件的连接处通过引入连接单元来模拟螺栓的滑移,研究了螺栓滑移对输电杆塔整体变形及承载能力的影响。文献[6-15]分别建立了精细化的输电杆塔杆梁混合模型,研究了舞动、覆冰、脱冰跳跃、断线等复杂工况条件下塔线体系的承载特征。以上方法均需要引入杆塔模型,在舞动等长时动态载荷作用下,大大增加了分析难度,降低了分析效率。李黎等[16]、楼文娟等[17]、晏致涛等[18]、Yan等[19]和周林抒等[20]等将杆塔直接简化为固定约束挂点,研究了舞动等复杂工况条件下线路的振动特征。以上方法均忽略了杆塔与导线间的耦合作用,当舞动等动载较大时,该简化方法的计算精度需要进一步进行验证。
为解决现有输电线路塔线体系计算精度和计算效率之间的平衡问题,提出一种基于等效刚度的输电线路杆塔简化等效方法,采用典型的大刚度直线塔和小刚度耐张塔验证在舞动条件下该方法的适用性,并分析传统固定约束等效方法存在的不足,以期研究结果对于塔线体系的振动特征及破坏原因分析具有重要的指导意义。
1 基于等效刚度的输电杆塔简化分析方法
1.1 杆塔等效刚度简化模拟方法
输电杆塔主要由通过螺栓连接的单根角钢拼装而成。目前在研究输电线路的振动及受力特性研究时,常用杆塔处理方法有三种:①建立完全精细化的三维实体模型,包括螺栓与杆塔塔材的连接关系等,该方法可以准确反映杆塔各个构件的接触特性,准确反映杆塔的局部承载特性,但该方法计算量大、收敛性差,常在做局部分析时采用;②建立精细化杆梁混合模型,该方法能准确反映杆塔的整体受力特性以及杆塔与导线的相互影响,但其同样具有计算量较大的缺点;③将杆塔等效为完全固定约束的连接点,忽略杆塔与导线之间的耦合作用,该方法计算量小、方便快捷,但是可能会影响塔线耦合体系的计算精度。

图2 HZ-60直线塔挂点各方向载荷与位移关系
因此,在保证计算精度的条件下,为了提高塔线体系计算分析速度,提出一种杆塔等效刚度建模等效方法。该方法首先建立杆塔的精细化杆梁混合模型,通过在杆塔的挂点处分别施加X、Y和Z三个方向的载荷,获取杆塔挂点处的对应位移,建立施加载荷与对应位移之间的关系,从而获得杆塔挂点处三个方向的等效刚度。在后续开展输电线路振动及受力分析时,采用弹性单元来代替塔线耦合体系中的输电杆塔,从而实现塔线体系的快速模拟分析,该弹性单元三个方向刚度与获取的挂点等效刚度一致。
1.2 典型直线和耐张杆塔等效刚度
主要以HZ-60直线塔和CJ1-30耐张塔为例,介绍典型杆塔的等效刚度模拟方法。杆塔模型如图1所示。
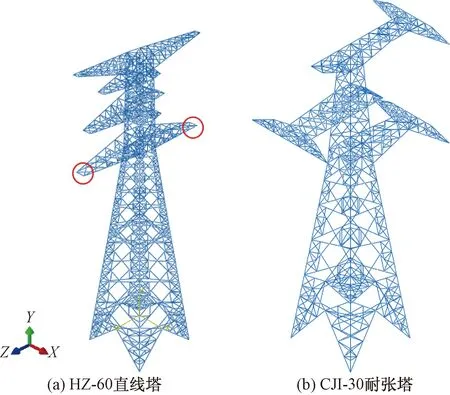
图1 典型直线塔和耐张塔
通过在如图1所示的杆塔下横担挂点处施加X、Y和Z方向的载荷,模拟获得杆塔的载荷和位移之间的相关关系,如图2所示。由图2可知,在杆塔连接完好,塔材在线弹性变形范围内,挂点三个方向载荷位移呈明显的线性关系,通过载荷与位移之间的斜率关系,求得两典型杆塔的简化等效刚度,见表1。由表1可知,HZ-60直线塔和CJ1-30耐张塔均在Y方向具有最大的等效刚度分别为54.453×106N/m和11.121×106N/m,HZ-60直线塔刚度远大于CJ1-30耐张塔。在后续分析中,将直接采用基于该等效刚度的弹性单元代替杆梁混合模型研究整体线路特征。

表1 两种典型杆塔等效刚度
2 舞动条件下杆塔等效刚度方法适用性研究
输电线路舞动具有频率低、振幅大、持续时间久等特点,是影响冬季线路安全运行的重要因素。将采用精细化杆梁混合模型、传统固定约束等效方法和本文提出的杆塔等效刚度简化方法分别模拟研究大刚度直线塔和小刚度耐张塔在舞动过程中的导线舞动特征,验证本文所提等效方法的适用性。
在此采用文献[21]中提出的舞动数值模拟方法研究不同杆塔等效方法的舞动特征。该舞动数值模拟方法与国网输电线路舞动防治技术重点实验室现场舞动实测数据进行了对比验证,验证了该舞动数值模拟方法的准确性。
2.1 大刚度输电杆塔等效方法适用性研究
2.1.1 有限元模型建立
以1.2节中等效刚度较大的直线塔为对象,采用三种方法分别建立两塔三档线路有限元模型,如图3所示。其中图3(a)为精细化杆梁混合模型,图3(b)为提出的等效刚度有限元模型;简化时将杆塔挂点处X、Y、Z三个方向采用等效刚度的弹性单元代替输电杆塔;图3(c)为传统的固定约束模型,简化时将杆塔挂点完全约束。线路档距均为200 m,导线型号为4XLGJ-400/50,直径为27.6 mm,初始安装张力为27.09 kN。每档导线按照等间距安装3个间隔棒,导线分裂间距为0.45 m。导线覆冰形状为新月形,厚度为12 mm,风速为12 m/s,基于中国空气动力研究和发展中心低速空气动力研究所1.4 m×1.4 m低速风洞中风洞试验测试,研究获得了新月形覆冰四分裂导线的静态气动特性,如图4所示,研究舞动采用的初始风攻角50°。
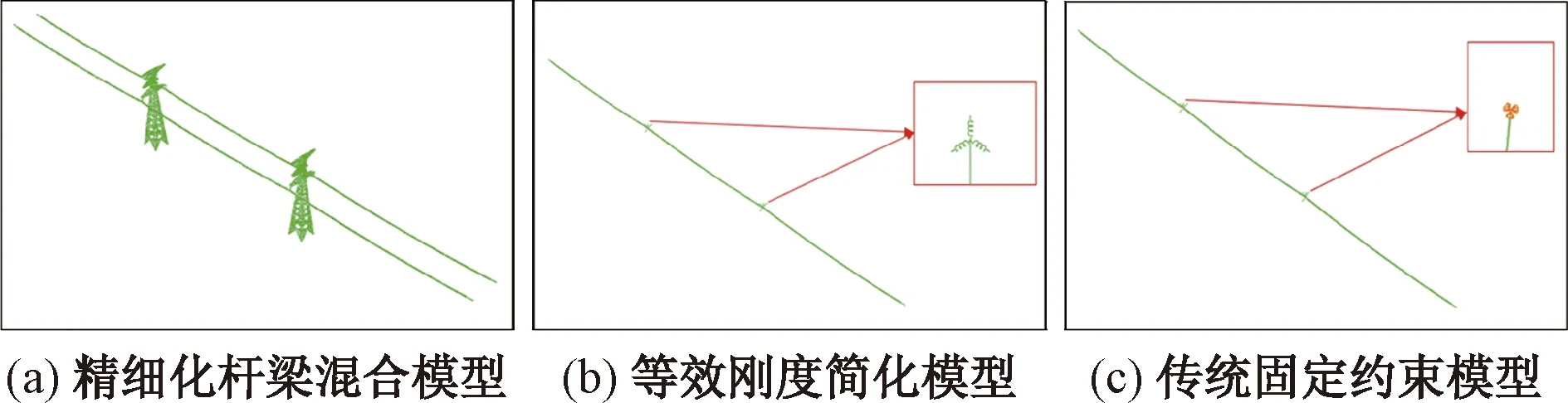
图3 三种典型有限元模型 (直线塔)

图4 新月形覆冰四分裂导线各子导线气动系数随风攻角的变化规律
2.1.2 线路动力特性对比
为了分析三种杆塔简化方法对线路舞动特征的影响规律,首先基于建立有限元模型,分析获得三种杆塔处理方法对应的输电线路面内、面外和扭转方向的低阶固有频率和模态特性,计算结果如表2所示,典型低阶模态如图5所示。可以看出,挂点处采用不同连接方式的三个线路模型在面内、面外、扭转三个方向的固有频率差异极小,几乎一致,说明提出的基于等效刚度的杆塔简化方法能有效地反映杆塔的动态特性。
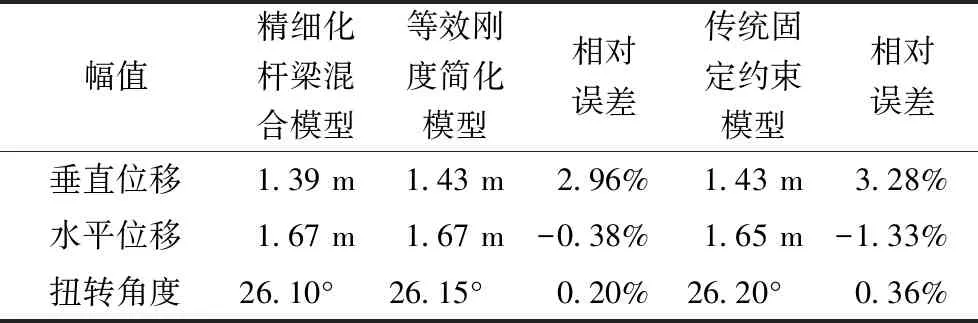
表2 三种模型中间档导线中点幅值(RMS)对比

图5 三种简化方法对应的线路塔线体系低阶固有频率和模态
2.1.3 大刚度杆塔等效简化对线路舞动的影响
用建立的有限元模型和风洞试验测得的气动系数,分别采用精细化杆梁混合有限元模型、提出的等效刚度方法和传统固定约束简化方法分别研究大刚度两塔三档覆冰四分裂导线的舞动过程。
图6给出了12 m/s风速条件下三种方法计算得到的中间档导线中点在舞动过程中的竖直位移、水平位移和扭转角时程曲线。由图6可知,在刚度较大时,三种方法得到的线路舞动振动特征十分接近,时程曲线十分接近。此外,表2给出了三种模型中间档导线中点幅值(RMS)对比,由表2可知,本文等效刚度模型与精细化模型相比最大误差仅为2.96%,具有很高的精度;传统挂点约束模型最大误差为3.28%,略大于本文等效刚度模型,这是由于杆塔较大时,两种简化方法均接近于固定约束,误差比较接近,均能较准确地描述舞动条件下杆塔的振动特征。
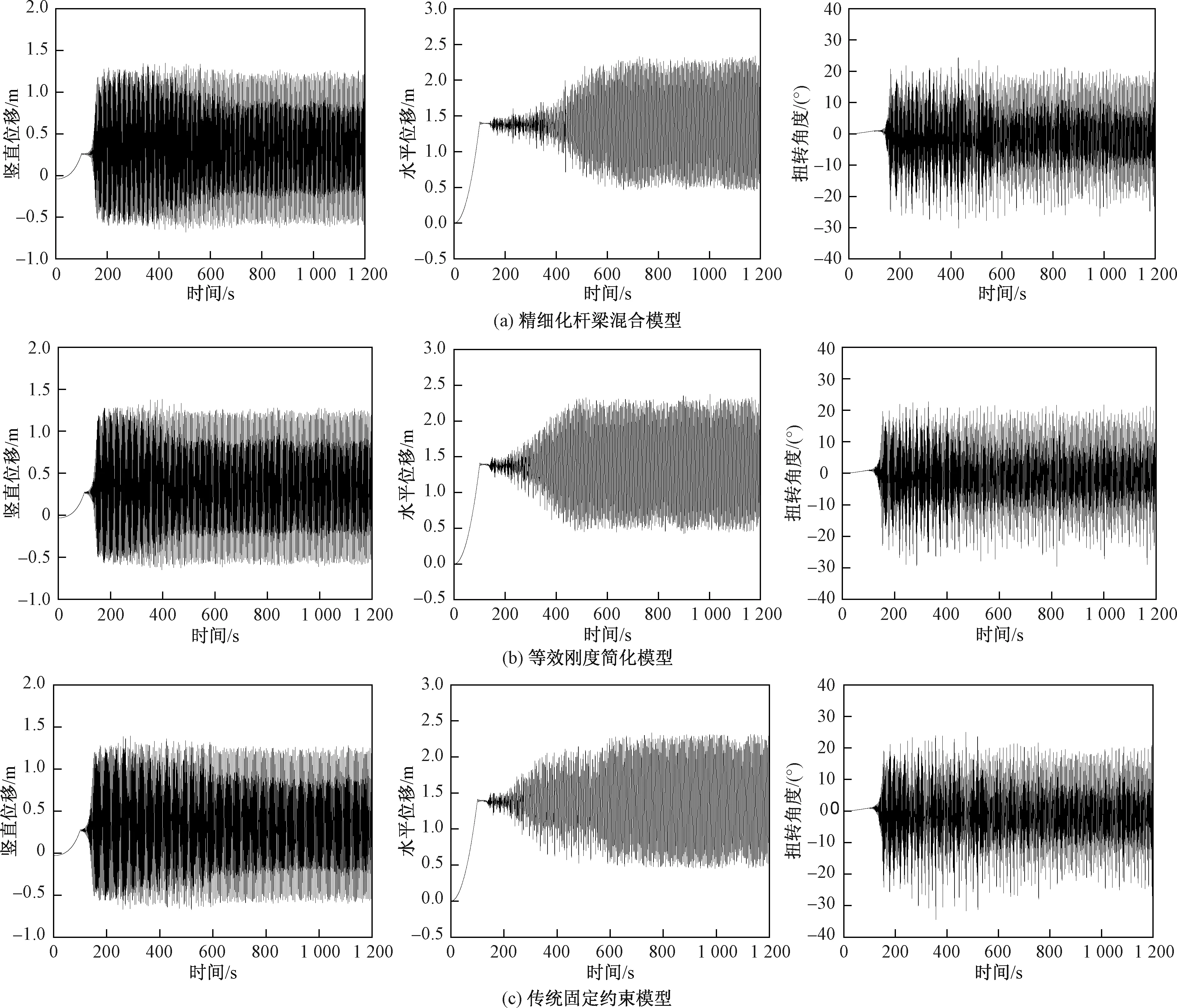
图6 中间档导线子导线1中点处位移和扭转角时程
表3给出了三种模型导线中间点舞动频率对比,图7给出了三种方法获得的中间档导线子导线1中点处位移和扭转角频谱。由图7和表3可知,三种方法得到的导线竖直、水平位移和扭转角频谱峰值十分接近,分别出现在0.446、0.226和0.446 Hz附近。此外,三种方法获取的导线振动形态和频率也完全一致,如图8所示。这表明本文杆塔等效方法和传统的挂点约束方法均能有效描述线路的舞动特征。
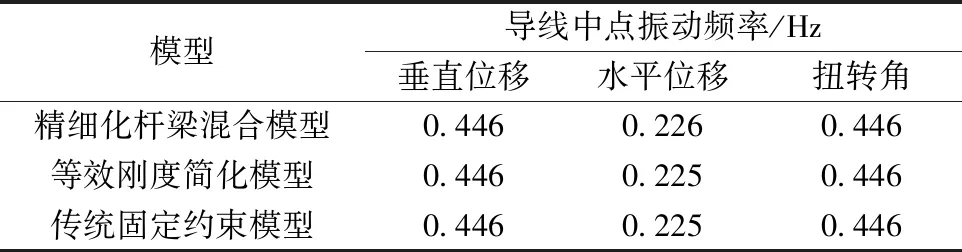
表3 三种模型导线中间点舞动频率对比
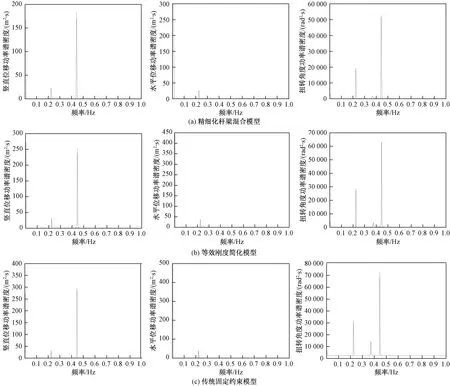
图7 中间档导线子导线1中点处位移和扭转角频谱
综上,对于刚度较大的输电杆塔,本文等效刚度简化模型和传统固定约束简化方法模拟得到的舞动振幅与精细化杆梁混合模型结果误差较小,均不超过3.3%,其中等效刚度简化模型较传统固定约束模型具有更高的精度,故可采用等效刚度模型对塔线体系进行简化计算。
2.2 小刚度输电杆塔等效方法适用性研究
以1.2节中等效刚度较小的耐张塔为对象,采用三种方法分别建立线路有限元模型,如图9所示。其中图9(a)为精细化杆梁混合模型,中间档为一孤立档;图9(b)为本文刚度等效有限元模型,简化时将杆塔挂点处X、Y、Z三个方向采用等效刚度的弹性单元代替输电杆塔;图9(c)为传统固定约束模型,简化时将杆塔挂点端部完全约束。导线、覆冰等结构参数与2.1节中线路参数保持一致。
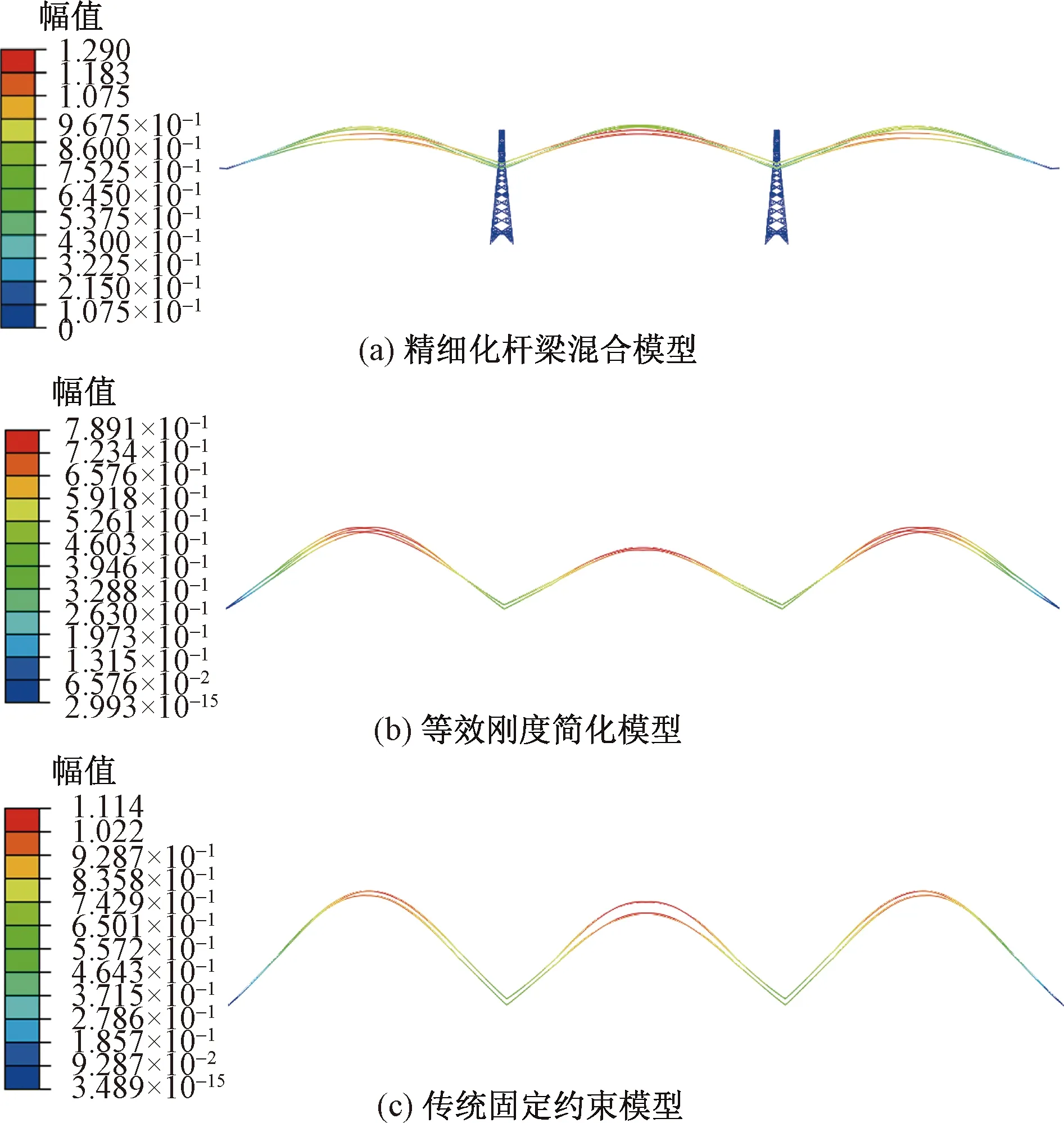
图8 中间档导线子导线1中点处位移云图
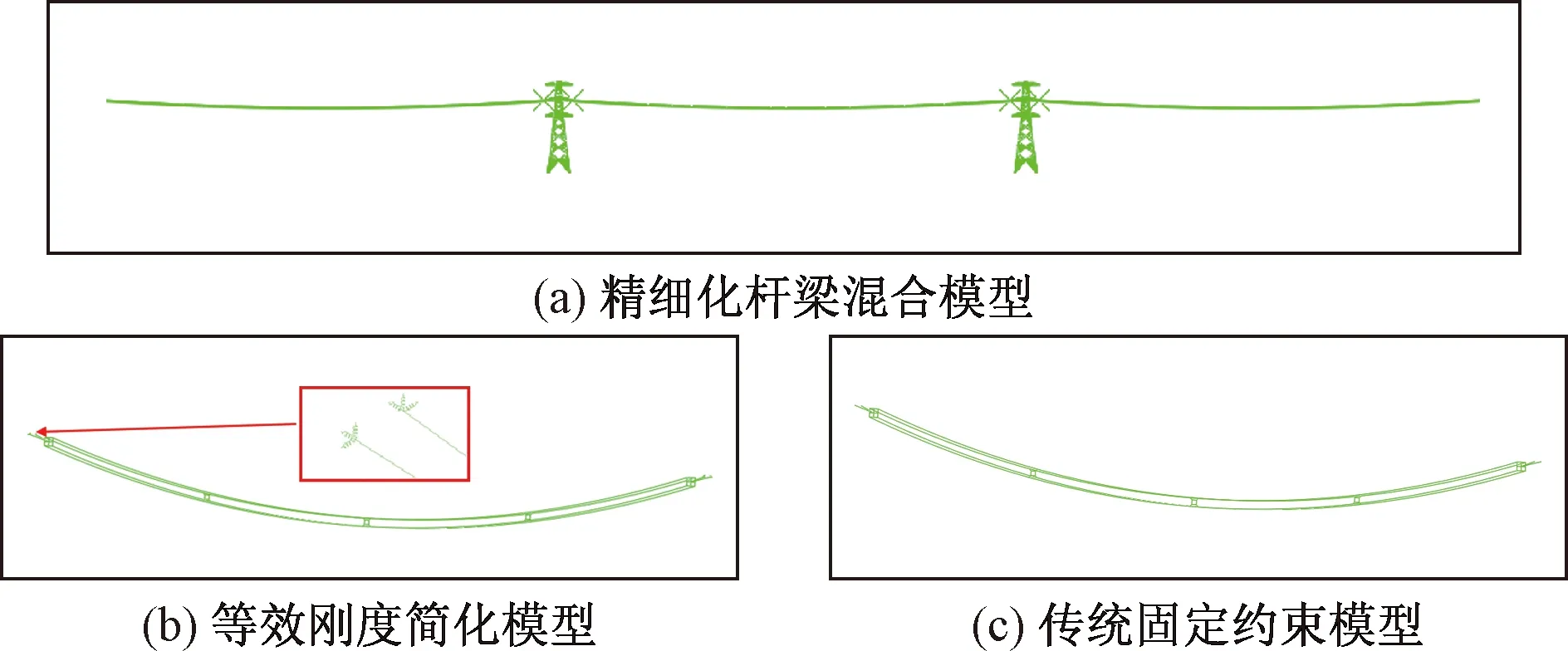
图9 三种典型有限元模型(耐张塔)
基于建立的有限元模型和风洞试验数据,分别采用三种简化方法研究小刚度耐张塔四分裂导线的舞动特性。表4分别给出了精细化有限元模型、本文所提等效刚度模型和传统固定约束模型三种方法对应导线中点垂直、水平位移和扭转角振幅的RMS。由表4可知,等效刚度模型与精细化模型相比最大误差为9.50%,具有较高的精度,而传统固定约束模型最大误差为60.58%,远大于本文等效高度模型。因此,刚度较小时,传统固定约束简化方法将不能准确描述杆塔的振动特征,而本文杆塔等效刚度简化模型仍具有较高的精度,能满足线路特征分析要求。
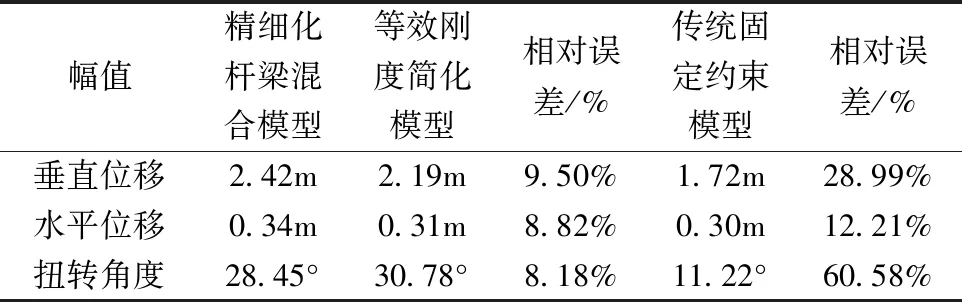
表4 三种模型导线中点振幅对比
现通过对子导线1中点处的位移和扭角频谱分析,获得三种杆塔处理方法对应线路的舞动振动形态和频率特性,见表5。由表5可知,精细化杆梁混合模型的竖直位移、水平位移和扭转角振动频率均为0.470 Hz,本文等效刚度简化模型三个方向振动频率均为0.450 Hz,而传统固定约束模型三个方向振动频率均为0.435 Hz。因此,本文杆塔等效刚度简化方法模拟得到的线路振动频率较传统固定约束方法而言,与精细化杆梁混合模型更为接近,具有更高的精度,更能准确地反映杆塔的振动频率特征。
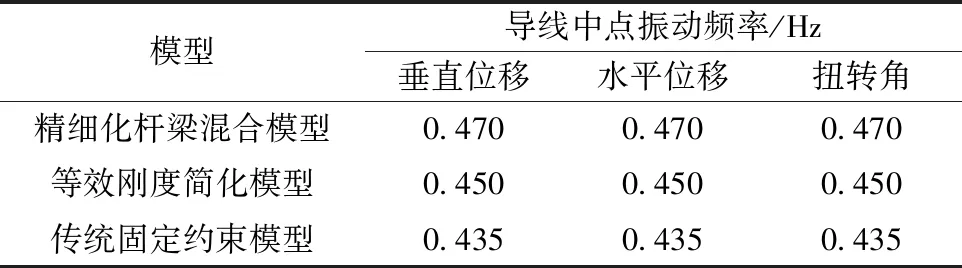
表5 三种模型导线中点舞动频率对比
综上,当杆塔刚度较小时,传统固定约束等效简化方法在研究舞动特征时,振动幅值和频率均具有较大的误差,而本文中提出的等效刚度模型则能更为准确的描述线路的舞动特性,故采用等效刚度模型对塔线体系进行简化计算是可行的。
3 结论
给出了一种基于刚度等效的输电线路杆塔等效方法,并采用数值模拟方法验证了算法的合理性。在此基础上,结合风洞试验数据,研究了基于等效刚度的杆塔简化等效方法对线路舞动的影响,得到以下结论。
(1)与精细化杆梁混合模型相比,基于等效刚度的杆塔简化方法能准确描述杆塔各个方向的刚度特性,两种杆塔处理方法对应线路的动力特性完全一致。
(2)当杆塔刚度较大时,本文杆塔等效刚度简化方法和传统固定约束等效方法均能较有效地模拟杆塔对线路舞动特征的影响,其舞动位移和扭转时程与杆梁精细化混合模型相比最大误差不超过3.3%,其中等效刚度模型较传统固定约束模型具有更高的精度,研究舞动时均可采用。
(3)当杆塔刚度较小时,本文等效方法与精细化杆梁混合模型研究获得的舞动幅值、振动频率等特征参数十分接近,最大误差不超过10%,而传统固定约束简化方法的扭转角度最大误差高达60.58%。因此,在研究线路舞动时,本文基于等效刚度的杆塔简化方法能更有效准确地模拟线路的舞动特征。
(4)与精细化简化模型相比,本文中基于等效刚度的杆塔简化模型具有计算效率高,快捷简单等特点,能快速模拟不同工况条件下线路的振动特征,对于线路塔线体系在复杂工况下动力响应特征的研究具有指导意义。
