电液负载模拟器神经网络辨识器及控制器设计

2020-04-22刘晓琳陈立东

科学技术与工程 2020年2期

刘晓琳，李卓，陈立东

(中国民航大学电子信息与自动化学院，天津 300300)

飞机围绕纵轴、横轴、立轴旋转都要由相应的舵机分别驱动副翼、升降舵和方向舵来实现倾斜、俯仰和航向控制。舵机是飞行控制系统的重要组成部分，也是飞机的执行机构，其控制性能优劣直接影响飞机的飞行品质[1]。舵机在真实飞行过程中会受到各种空气力载荷的影响，且载荷大小随飞行高度、速度、姿态及气流等因素的改变而发生变化。在实验室条件下，通常使用电液负载模拟器模拟舵机在飞行过程中所受到的各种力载荷的变化情况，验证舵机在不同飞行状态下的工作性能，进行静态、动态技术指标的检查和测试，从而将传统的自破坏性全实物仿真试验转化为实验室条件下的预测性研究[2]。

虽然电液负载模拟器在很大程度上改进了舵机的测试方式，具有可控性、无破坏性的优点。但是对于被动式力伺服控制系统来说，由于电液负载模拟器的输入伺服指令与承载对象舵机的运动相关，所以由舵机的主动运动产生的外部扰动即多余力[3]，将会严重影响伺服控制系统的加载精度及动态性能。鉴于此，针对飞机舵机电液负载模拟器存在的多余力干扰的问题，结合系统工作原理与结构特点，重建控制器结构功能及控制策略，从而实现舵机在实际工作过程中所受力载荷的真实模拟能力，满足电液负载模拟器对稳定特性、加载精度、响应速度、跟踪能力等技术指标的要求[4]。

1 电液负载模拟器数学模型建立

1.1 系统结构及工作原理

电液负载模拟器由舵机子系统、加载子系统、连接机构三部分构成，其结构框图如图1所示。其中，舵机子系统由舵机伺服阀、舵机液压缸和位移传感器等组成，加载子系统由控制器、加载伺服阀、加载液压缸和力传感器等组成。舵机子系统根据控制计算机发出的位移指令信号，经由舵机伺服阀驱动产生主动运动。加载子系统控制器设置加载梯度，然后与位移传感器反馈的舵机实际位置信号相乘，计算出舵机在该条件下实际所受的力载荷值，经由连接机构加载到舵机上[5]，从而完成电液负载模拟器力载荷的加载工作。

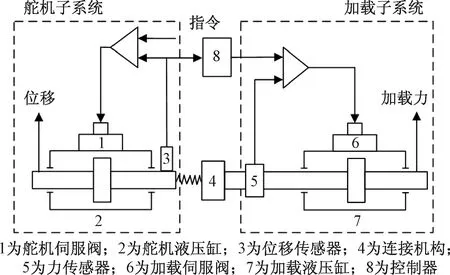
图1 电液负载模拟器结构框图

电液负载模拟器的加载子系统通过金属-橡胶缓冲弹簧与舵机子系统相连接。由于舵机本身的主动运动迫使加载液压缸两腔产生强迫流量，从而使加载子系统产生多余力，导致实际加载力跟踪指令力的效果不佳，进而影响负载模拟器的加载性能。因此，电液负载模拟器是一个复杂的被动式力伺服控制系统。

1.2 系统数学模型

电液负载模拟器结构复杂，一方面由于加载子系统油液温度、液压缸内部摩擦以及缓冲弹簧的阻尼系数等非线性因素影响较多[6]，另一方面舵机子系统与加载子系统在工作过程中会产生多余力干扰，且各种干扰因素之间存在耦合[7]，理论上很难建立电液负载模拟器全部结构的数学模型。因此，本文根据其工作原理及结构特点，建立实际数学模型，为后续控制器设计及多余力抑制研究提供理论依据。

加载液压缸是加载子系统重要的组成元件，其工作原理是根据加载伺服阀阀芯位移控制内部液压油流量变化，从而实现负载模拟器力载荷的加载工作[8]。加载液压缸的数学模型主要由加载伺服阀线性化流量方程、加载液压缸连续性方程及加载液压缸与负载力平衡方程组成，经线性化处理及拉普拉斯变换后得到：

Qf=KQxv-KcePf

(1)

式(1)中：Qf为输出负载流量变化；KQ为伺服阀流量系数；xv为伺服阀阀芯位移；Kce为伺服阀流量压力系数；Pf为液压缸两端产生的负载压降。

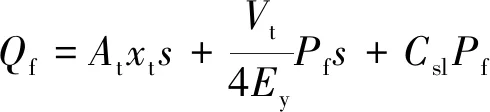
(2)

式(2)中：At为液压缸活塞有效作用面积；xt为活塞位移；Vt为液压缸有效容积；Ey为等效容积弹性模量；Csl为液压缸总泄露系数。

AtPf=mtxts2+Btxts+F

(3)

式(3)中：mt为活塞与负载的等效总质量；Bt为活塞黏性阻尼系数；F为系统实际加载力。

考虑到加载子系统技术要求频率为10 Hz，而加载伺服阀固有频率一般高于70 Hz，因此可将加载伺服阀数学模型看作比例环节，经简化后得到传递函数为

(4)

式(4)中：ui为加载伺服阀输入电压即控制电压；Ksv为加载伺服阀增益。

在电液负载模拟器结构中设置金属-橡胶缓冲弹簧，不但可以减小多余力干扰，而且其变刚度连接特性可实现力载荷的连续性加载。忽略缓冲弹簧本身质量及弹性摩擦系数，得到加载子系统实际加载力信号，并将其转换成一定比例的电压信号为

F=Kt(xt-xy)

(5)

(6)

式中：Kt为缓冲弹簧连接刚度；xy为舵机子系统输出位移；Kf为力传感器增益。

根据式(1)～式(6)，得到电液负载模拟器数学模型，如图2所示。

图2 电液负载模拟器数学模型

2 电液负载模拟器复合控制器设计

从电液负载模拟器的工作原理及数学模型可以看出，它既是一个复杂的机电液复合控制系统，又是一个具有非线性、不确定性、参数时变的强耦合控制对象。其中，加载子系统指令力受舵机子系统主动运动的干扰，而舵机子系统在运行过程中一方面由计算机给定位移指令信号控制，另一方面受加载子系统实际加载力影响，从而使加载子系统与舵机子系统相互耦合，产生多余力干扰[9]，严重影响电液负载模拟器的跟踪精度、响应速度及稳定性能。

鉴于此，在设计控制器时既要满足系统性能指标的要求，又要考虑控制策略的可行性和有效性，设计一种基于神经网络辨识器-控制器(neural network identifier and neural network controller, NNI-NNC)的复合控制器结构，利用神经网络系统辨识功能和自适应实时控制策略，以提高电液负载模拟器的动态品质。NNI-NNC复合控制器原理如图3所示。

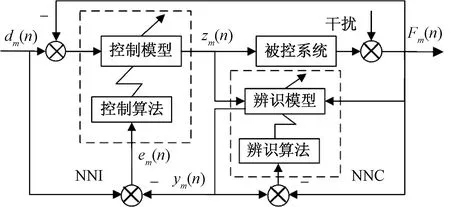
dm(n)为加载子系统指令力；Fm(n)为实际加载力；ym(n)为辨识模型输出力；zm(n)为神经网络控制器输出；em(n) 为指令力与模型输出力的偏差

2.1 神经网络辨识器设计

基于电液负载模拟器的结构复杂性和测试需要，在设计控制器之前，对理论数学模型进行辨识是关键。由于反向传播(back propagation，BP)神经网络具有学习速度快、可以逼近任意非线性连续函数、并行处理复杂数据的特点，同时其动态调整结构参数、在线辨识多变量系统的能力可以很好地解决非线性复杂系统模型参数辨识的问题[10]，因此采用BP神经网络辨识器建立电液负载模拟器神经网络辨识模型。

为了避免常规BP神经网络易出现陷入局部最小值的现象，在实际应用中常引入学习步长η来改善网络逼近非线性函数的学习速度[11]。网络学习速度与系统稳态性能产生关联，若学习步长η过大，则网络学习过程发生振荡，导致系统稳态性能变差；反之，若学习步长η过小，则网络收敛速度减小，导致系统动态性能不佳。鉴于此，为了有效解决系统学习速度与稳态性能之间的矛盾，对BP神经网络模型结构进行改进，通过引入“动量因子α”对网络隐含层权值补偿训练规则及网络输出层权值修正部分进行在线整定，从而提高网络模型辨识效果。

结构改进后的BP神经网络优化算法工作流程如下。

选取学习样本总数P，设定BP神经网络隐含层数目为1，设计网络输入层神经元为i(i=1,2,…,M)，隐含层神经元为j(j=1,2,…,L)，输出层神经元为k(k=1,2,…,N)。

设计网络权值及阈值初值为[-0.5，0.5]的随机数，计算网络隐含层输入函数netj，再以S函数为激活函数，得到隐含层神经元输出函数为

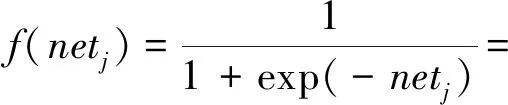
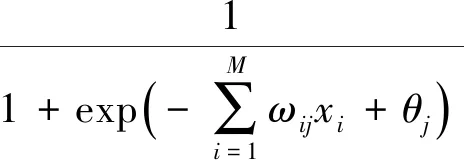
(7)

式(7)中：ωij为输入层与隐含层之间的连接权值；θj为隐含层神经元阈值。

同理可得网络输出层神经元输出函数为

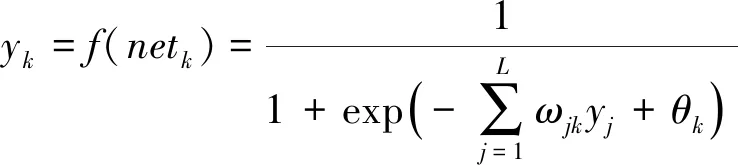
(8)

定义期望输出函数为Yk，则目标函数为网络全局误差函数：

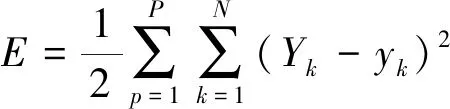
(9)

采用最速下降法，引入学习步长η反向计算网络权值，即

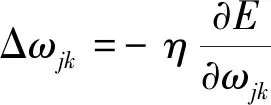
(10)

为提高网络收敛速度及稳定性，在常规权值调整的基础上，引入动量因子α，则优化后网络输出层权值修正公式为

ωjk(n+1)=ωjk(n)+Δωjk+αk[ωjk(n)-

ωjk(n-1)]

(11)

同理可得网络隐含层权值修正公式为

ωij(n+1)=ωij(n)+Δωij+αj[ωij(n)-

ωij(n-1)]

(12)

采用上述BP神经网络优化算法对电液负载模拟器数学模型进行辨识的工作过程描述如下：

首先，对数学模型进行离散化处理，以获取网络输入输出神经元。该离散化模型为

F(n+1)=f[F(n),F(n-1),F(n-2),ui(n),

ui(n-1),ui(n-2),xy(n),xy(n-1),xy(n-2)]

(13)

然后，确定网络模型输入层、隐含层、输出层神经元数目为4-7-1。其次，由于辨识模型的输出力信号与加载子系统的实际加载力及控制电压有关，为了确保辨识器在线调整结构参数的准确性，故选取ui(n)、ui(n-1)、F(n)及F(n-1)作为输入神经元，选取F(n)作为输出神经元。最后，设定网络每组样本训练次数R=300，动量因子α=0.4，学习步长η=0.7，容许误差ε>0，再按照式(7)～式(13)优化算法工作流程对网络进行训练。

神经网络辨识器训练结果如图4所示。由图4分析可知，随着神经网络学习深入与学习速度的加快，网络辨识模型输出曲线能够近似逼近理论模型输出曲线，而且目标函数位于一定误差带之内，满足系统容许误差的要求。结果表明，本文所提出的BP神经网络辨识器可以很好地反映电液负载模拟器的动态特性，准确辨识非线性复杂系统的结构模型。另外，对常规BP神经网络引入动量因子进行优化，可以有效提高网络的学习速度和鲁棒性。

图4 神经网络辨识器训练结果

2.2神经网络控制器设计

从神经网络辨识器训练结果可以看出，虽然BP神经网络优化算法可以很好地解决非线性复杂系统辨识问题，但是由于多余力干扰严重，导致加载力跟踪效果不佳，将无法满足电液负载模拟器的加载要求和测试需要，所以采用神经网络辨识器与神经网络控制器相结合的复合控制器来抑制多余力干扰。

Adaline网络自学习过程是通过对多个输入变量的线性加权求和，进行系统参数的连续性自动调节，获得具有良好逼近性能的单一输出变量，从而实现系统自适应控制，具有结构简单、学习速度快、自适应强的优点[12]。因此以神经网络辨识模型为控制对象，采用Adaline网络控制器监督电液负载模拟器参数及多余力干扰的变化情况，实现系统自适应鲁棒控制。

设定加载子系统指令力为dm(n)，实际加载力为Fm(n)，辨识模型输出力为ym(n)，神经网络控制器输出为zm(n)，则

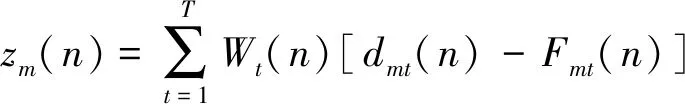
(14)

式(14)中：T为神经元突触个数；W(n)为Adaline网络权值；m为当前样本组数。

采用梯度下降法实现网络权值调整，选择指令力与模型输出力的偏差em(n)作为误差信号，则误差能量函数为

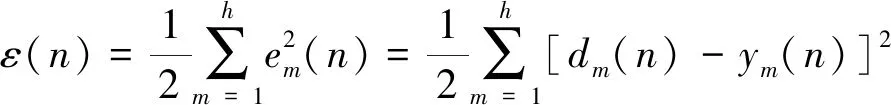
(15)

式(15)中：h为样本总数。

确定Adaline网络权值调整公式为

Wt(n+1)=Wt(n)+ΔWt(n)

(16)

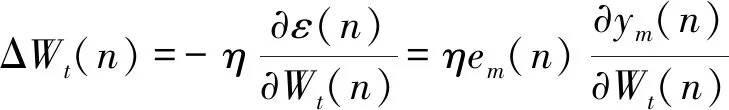
(17)

式中：

[dmt(n)-Fmt(n)]f′[netk(n)]；

[dmt(n)-Fmt(n)]wij(n)wjk(n)f′[netk(n)]×

f′[netj(n)]

(18)

由此可得：

Wt(n+1)=ηem(n)wij(n)wjk(n)f′[netk(n)]×

f′[netj(n)][dmt(n)-Fmt(n)]+Wt(n)

(19)

本文中提出的神经网络控制器与传统控制方案相比，具有以下两个特色与创新之处。

(1)采用指令力与实际加载力之间的偏差作为网络学习样本的控制策略，可以有效补偿多余力等非线性干扰带来的控制误差。另外，利用指令力与辨识模型输出力之间的误差信号和BP神经网络反向递归计算，能够综合确定网络权值修正准则。

(2)利用神经网络控制器对神经网络辨识器进行监督控制，可以实现控制参数在线整定，从而提高电液负载模拟器在线辨识的实时性及动态稳定性。

3 系统仿真实验与结果分析

利用MATLAB计算机仿真平台，应用不同加载梯度及系统运行频率的指令信号来验证电液负载模拟器NNI-NNC复合控制器的控制性能。根据飞机舵机工作频率为1～20 Hz，加载梯度为1～30 N/mm，设置系统结构参数为KQ=4.63 m2/s，Kce=6.7×10-11m5/N，At=0.015 m2，Vt=0.004 8 m3，Ey=4×108N/m2，mt=300 kg，Bt=0.000 1 N·s/m，Ksv=0.43 m/A，Kf=0.34 V/N，Kt=8×106N/m；网络初始参数为R=300，α=0.4，η=0.7。

3.1 系统稳定性及多余力抑制效果实验

为了验证NNI-NNC复合控制器对系统多余力的抑制效果，设置系统加载梯度为1 N/mm，指令力是幅值为0.7 mm、频率为10 Hz的正弦信号，由此得到系统未采用补偿方法加载和采用复合控制器加载时的多余力抑制效果曲线如图5所示。

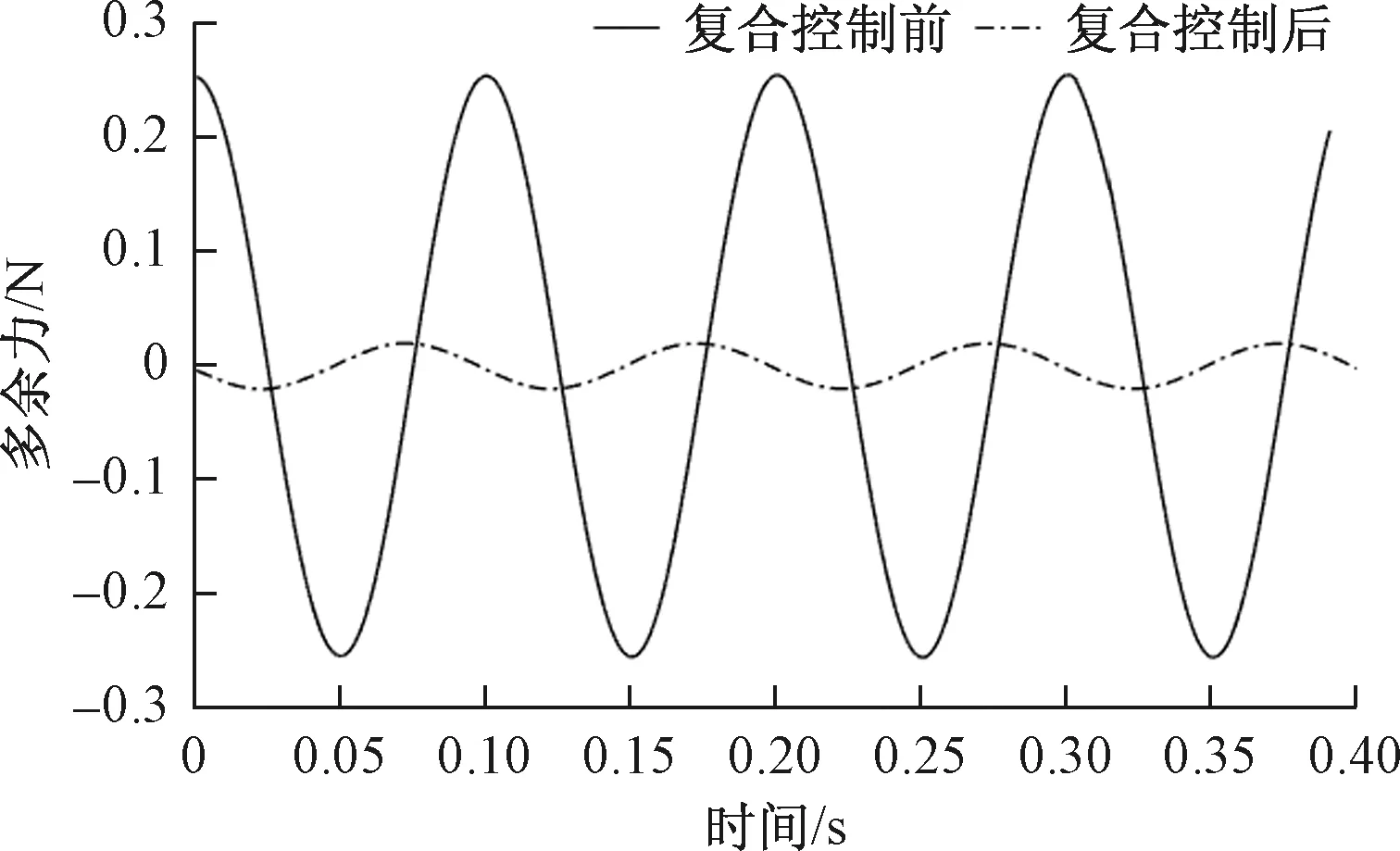
图5 多余力抑制效果实验曲线

由图5分析可知，在系统未采用复合控制器时，多余力干扰严重，最大可达0.25 N，系统稳定性较差。采用复合控制器后，系统多余力得到明显抑制，最大可降至0.02 N，多余力消扰率可达92%，系统动态稳定性好。由此可见，采用NNI-NNC复合控制器加载时的多余力抑制效果得到改善，并且在保证系统稳定性的同时改善了电液负载模拟器的工作性能。

3.2 系统加载精度及跟踪性能实验

小梯度加载是指满足系统技术指标前提下的加载梯度的较小值，是衡量系统能否在极端条件下工作的关键指标[13]。为了验证小梯度加载时系统的加载精度及跟踪性能，特利用不同加载梯度的正弦信号进行激励，由此得到系统在NNI-NNC复合控制器控制下的动态响应曲线如图6～图8所示。其中，指令力是幅值为1 mm、频率为5 Hz的正弦信号。

根据图6～图8实验曲线的直观描述，按照指令力与复合控制器加载力的幅差、相差指标给出如表1所列的定量描述。

鉴于电液负载模拟器的工作性能指标为幅差小于10%，相差小于10%。由图6～图8所示曲线及表1数据综合分析可知，在小梯度加载条件下，系统虽然受到多余力等非线性因素干扰明显，导致幅差、相差与一般加载条件相比有所增加，但是复合控制器加载力仍能在满足系统工作指标条件下有效模拟飞机舵机所受到的力载荷干扰。由此可见，采用NNI-NNC复合控制器可以提高电液负载模拟器在小梯度加载极端条件下的加载精度及跟踪性能，为解决多余力干扰问题提供重要保障。

图6 加载梯度为1 N/mm跟踪曲线

图7 加载梯度为2 N/mm跟踪曲线

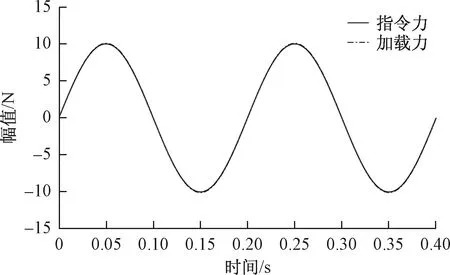
图8 加载梯度为10 N/mm跟踪曲线

表1 系统加载精度及跟踪性能实验结果

3.3 系统响应速度及鲁棒性实验

为了比较NNI-NNC复合控制器与常规增量式比例积分微分(Proportion Integral Derivative，PID)控制器的响应速度及鲁棒性，设置系统加载梯度为1 N/mm，指令力为单位阶跃信号，由此得到控制效果如图9所示。其中，加载力1为常规PID控制器的阶跃响应曲线，加载力2为单独采用神经网络控制器的阶跃响应曲线，加载力3为复合控制器的阶跃响应曲线。

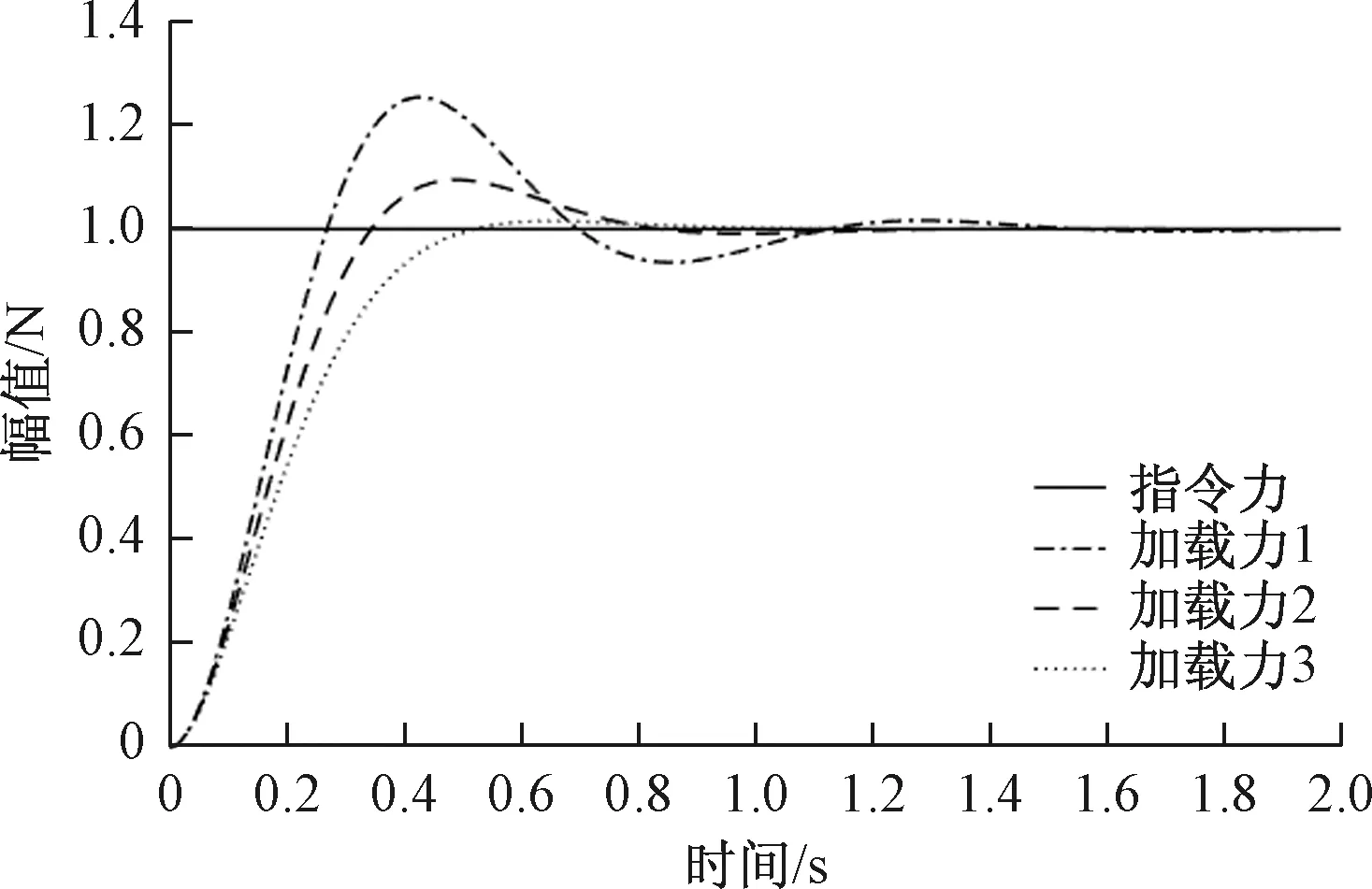
图9 系统响应速度实验曲线

由图9分析可知，在常规PID控制器作用下，系统调节时间为2.8 s，超调量为25.4%，系统鲁棒性较差；在神经网络控制器作用下，系统调节时间为2 s，超调量为6.8%，系统鲁棒性得到明显改善且产生较小振荡。在复合控制器作用下，系统调节时间为1.25 s，超调量为1.5%，系统鲁棒性显著提高。由此可见，神经网络控制器较常规PID控制器对系统控制性能及控制结构进行了有效改进，同时在此基础上结合神经网络辨识器后的复合控制器所得到的辨识模型更为接近电液负载模拟器的工作性能，具有良好的过渡动态品质。