基于密度峰值聚类的电力大数据异常值检测算法

陆春光, 叶方彬, 赵 羚, 姜 驰, 董 伟

(1.国网浙江省电力有限公司电力科学研究院，杭州 310007；2.浙江华云信息科技有限公司，杭州 310002)

电力大数据可被应用于智能电网的不同阶段[1-2]，对用电大数据进行挖掘有助于电网运营模式的转变[3-4]。但因为电力数据来源存在差异等问题和缺少数据质量控制机制，会造成异常数据形成[5]。异常数据即系统出现异常时的相关信息，有很大的研究价值，为实际故障排查与用电异常检测提供依据。

当前异常值检测算法主要有基于统计的异常值检测算法、基于聚类的异常值检测算法和基于分类的异常值检测算法等[6]。基于统计的异常值检测算法需假设数据集分布满足既定概率分布模型，将和模型不符的数据点当成异常值，但在实际应用中，电力大数据随机性很强，该方法不适于实际应用。基于聚类的异常值检测算法将不属于聚类簇的样本点当成异常值，部分聚类算法可直接获取异常值，但大部分聚类算法需求出聚类簇中样本点和中心间的间隔，以判断异常点，复杂度较高[7]。基于分类的异常值检测算法需有充足的标识样本，按照预测模型对没有分类的样本进行分类，获取异常类，该方法需要大量准确类别样本数据作为训练样本，不适于电力大数据异常值的检测。

为此，依据电力大数据特点，提出一种基于密度峰值聚类的电力大数据异常值检测算法，其基本思想为优化初始聚类中心，改善电力大数据异常值检测复杂度，提高了检测准确性与检测效率。经实例分析，所提方法可有效检测电力大数据异常值。

1 基于密度峰值聚类的电力大数据异常值检测算法

1.1 密度峰值聚类算法及其弊端分析

密度峰值聚类算法首先确定类中心点，再把电力数据点划分至和其间隔最小的有高密度值电力数据点所处的类中[8]。将聚类中心点看作局部密度最大点，通过启发式方法选择类中心点，将其称作决策图，决策群体中有两个关键的指标[9]，即局部密度ρi与距离δi。在决策群体中，假设待聚类电力大数据集用U={u1,u2,…,un}进行描述，相应指标集用IU={1,2,…,n}进行描述，Dij=dist(ui,uj)为电力数据点ui与uj间的某种间隔。

在电力数据点离散的情况下，局部密度ρi可通过式(1)求出：

(1)

式(1)中：j和i不相等同时均属于IU；函数γ(u)可描述成：

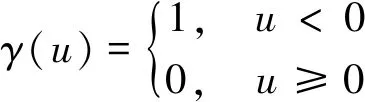
(2)

在数据点是连续的情况下，求出局部密度ρi：

(3)

式(3)中：Ds>0用于描述阶段距离；e为峰值聚类参数；ρi用于描述数据点ui的局部密度[10]，为U中和数据点ui间间隔低于Ds的电力数据点数量。

距离δi可通过式(4)求出：

(4)

式(4)中：对应指标集IU可描述如式(5)所示：

(5)

分析式(1)～式(5)可以看出，在密度数值中ρi是最大值的情况下，IU是空集，也就是没有密度高于ρi的数据点，当前ui是密度峰值点，δi用于描述U中和ui间隔最大的数据点和ui间的距离；反之，δi用于描述全部密度超过ui的电力数据点中和ui间间隔最小的数据点和ui间的距离。

密度峰值聚类算法可有效发现不同形状与密度的簇，但在选择聚类中心时忽略了δi与ρi对聚类中心选择的影响[11]，在选择聚类中心时需人工辅助决策，不但提高了聚类成本，还令聚类结果有一定的主观性，影响聚类精度，进而影响电力大数据异常值检测准确性。除此之外，密度峰值聚类算法会造成大量冗余复制与计算开销，无法满足电力大数据异常值检测。

针对上述两个弊端，对密度峰值聚类算法进行优化，将优化后算法应用于电力大数据异常值检测中。

1.2 密度峰值聚类中心确定

针对密度峰值聚类中心的弊端，对δi与ρi间的关系进行分析，提出依据δi与ρi的聚类中心选择策略，对密度峰值聚类算法进行优化。其基本思想如下：按照聚类中心选择原则，通过相邻距离δi和密度ρi的归一化乘积对聚类点的差异度进行衡量，按照差异度的统计特性与改变趋势选择最大的一组点当成聚类中心[12]，获取聚类中心后，按照相邻距离标号将电力大数据分割至不同簇，实现聚类。为了量化电力大数据某数据点偏移原点的程度，对δ与ρ进行归一化处理后，按照正比例关系，引入簇中心权值[13]：

ωi=δiρi

(6)

为了获取偏离度最大的数据点集，把簇中心权值按从大到小的顺序排列，取前N个点，N通常取30。将和原点偏离程度最大的点当成簇中心权值整体下降趋势从急到缓的拐点。

通过两点线段的斜率对测中心权值下降趋势进行描述：

(7)

(8)

在上述分析的基础上，给出簇中心选择过程：

(1)计算各电力数据点的差异度χ。

(2)把簇中心权值按从大到小的顺序排列。

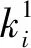
(4)将拐点前的电力数据点{1,2,…,v}当成簇中心点。

1.3 计算效率优化

本节按照空间z填充曲线与高维数据点z携带位置信息特性提出基于z的分布式密度峰值聚类算法[15]。

空间z填充曲线将d维空间映射为一维空间，所有电力数据点q的编号均和一个zq相应。图1描述的是一个二维空间中的z填充曲线贯穿为一个3×3的二维空间区域。

图1 z填充曲线示意图

d维坐标点Q(a1,a2,…,ad)的z计算过程如下：把十进制描述成二进制Q′(b1,b2,…,bd)，其中bi代表ai的二进制表述。按有效位降序与维度升序的顺序把Q′交叉排列转换成新的二进制数q(2)。把得到的二进制数q(2)通过十进制数描述成q(10)，q(10)就是点Q的z。

密度峰值聚类算法的基本思想为求出电力大数据集中各点的两个属性值密度值ρ与斥群值δ。对密度值ρ进行计算时，各点仅需和周围点计算距离即可[16]。求距离δ时，各点仅需和周围较其密度大的点计算距离即可。据此，给出如下详细优化过程：

(1)对电力大数据集X进行采样获取样本S，求出样本重点z与点对间的间隔，同时对距离值与z进行排序，对Ds与分组分位点集K={n1,n2,…,nn-1}进行估计。

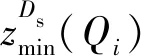
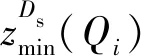
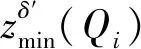
1.4 电力大数据异常值检测

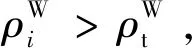
(9)

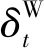
(10)

式(10)中：M用于描述电力大数据集的总量；ερ与εδ用于描述经验参数。

2 实验分析

为了验证基于密度峰值聚类的电力大数据异常检测算法的有效性，将某省交流配电变压器100d的电力数据作为实验数据。

在进行实验前，对电力数据进行标准化处理，公式如式(1)所示：

(11)

为了验证本文算法的有效性，将基于距离的检测算法和基于密度的检测算法作为对比进行测试。

基于距离的检测算法对任意两个电力数据的欧式距离进行计算，找到欧式距离最大的数据点，将欧式距离超过阈值的点当成异常值。基于密度的检测算法假设正常电力数据点的数据密度超过异常点的数值密度。

针对交流配电变压器电力数据，绘制电力大数据曲线，通过人工检测得到9个异常电力数据点，详细信息见表1。

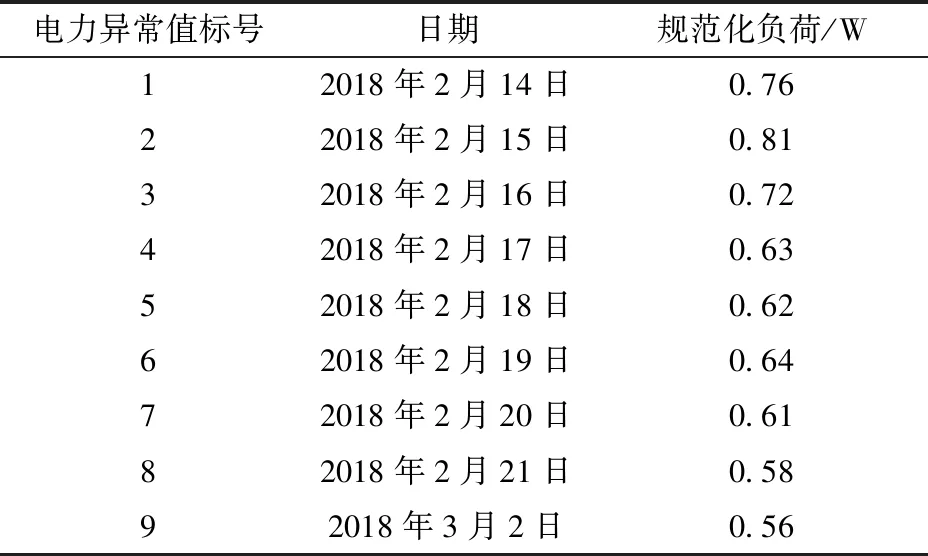
表1 人工检测得到的异常电力数据点信息

采用本文算法获取电力数据样本局部密度与局部距离，得到的电力大数据异常值检测结果用图2进行描述，图2中红色圆圈代表电力异常值。

分析图2，可得到9个异常电力数据点，这些数据点的详细信息见表2，发现异常电力数据点大部分发生在假期，和实际情况相符，说明本文算法检测得到的电力数据异常值准确。

图3描述的是采用基于距离的电力大数据异常值检测算法的检测结果。

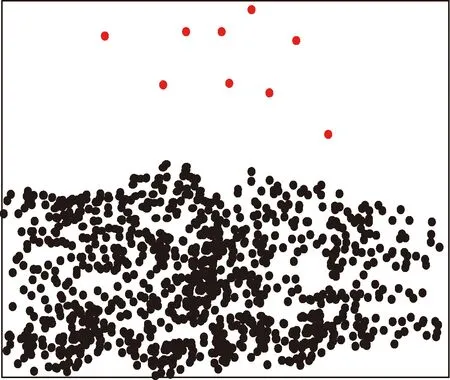
图2 本文算法电力大数据异常值检测结果

表2 本文算法检测电力异常数据点信息

基于距离的异常值检测算法检测的电力异常值详细信息见表3进行。

分析图3和表3可知，基于距离的异常值检测算法错误地把正常电力值检测为异常电力值，检测结果不准确。

图4描述的是采用基于密度的电力大数据异常值检测算法的检测结果。

基于距离的异常值检测算法检测的电力异常值详细信息见表4。

图3 基于距离的电力异常值检测算法结果

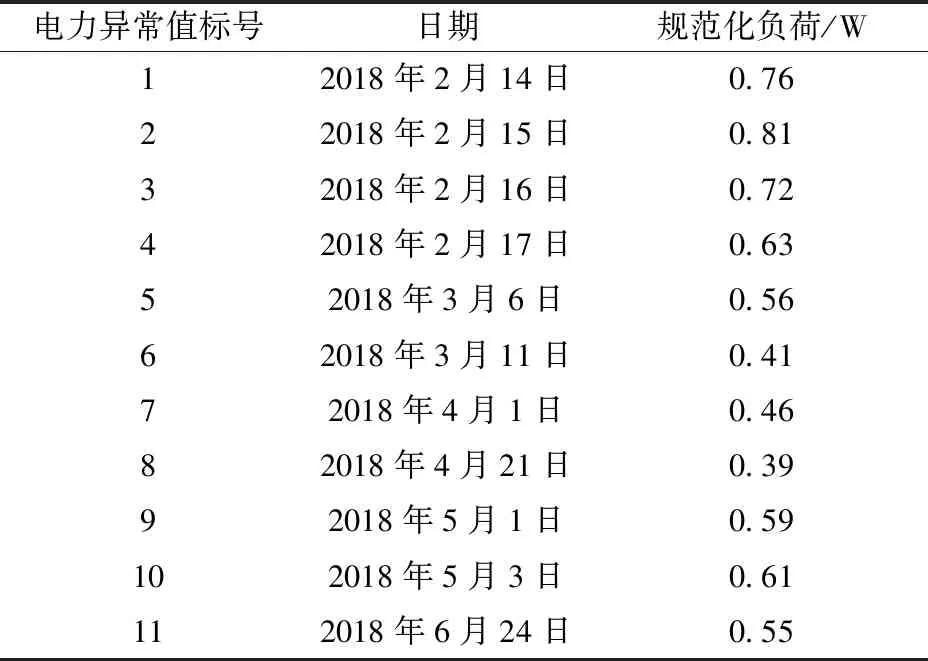
表3 基于距离的异常值检测算法检测结果

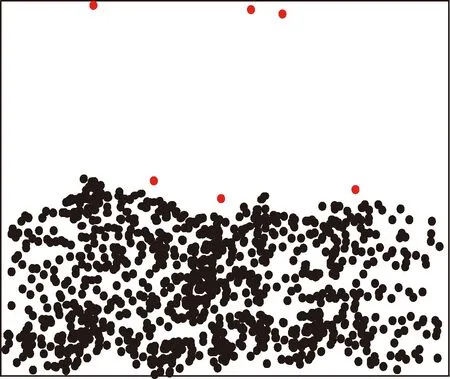
图4 基于密度的电力异常值检测结果

表4 基于密度的异常值检测算法检测结果

分析图4和表4可知，基于密度的检测算法检测结果和实际结果相比数量减少，且存在部分错误检测数据，与基于密度的检测算法相比，本文算法检测结果更加完整准确，可有效体现电力数据的异常情况。

3 结论

提出了一种基于密度峰值聚类的电力大数据异常值检测算法。分析了密度峰值聚类算法的聚类过程，发现该算法在选择聚类中心时需人工辅助决策，不但提高了聚类成本，还令聚类结果有一定的主观性，影响聚类精度，进而影响电力大数据异常值检测准确性。除此之外，密度峰值聚类算法会造成大量冗余复制与计算开销，无法满足电力大数据异常值检测。

提出相应的优化技术，在此基础上，将局部密度超过阈值，同时距离超过阈值的数值看作电力数据异常值，完成对其进行检测。

实验结果表明，所提算法可有效检测电力大数据异常值，且检测结果准确性高。