基于矿热炉外磁场信号的三相电极位置检测系统设计
2020-04-22牛群峰崔健超
王 莉,周 潼,牛群峰,崔健超
(河南工业大学电气工程学院,郑州 450001)
矿热炉是广泛应用于冶金、化工等行业的高耗能冶炼设备,主要通过三相自焙电极插入炉料,进行埋弧操作,将电能转化为热能,从而熔化矿石,实现金属冶炼[1]。在矿热炉冶炼的过程中,由于电极的消耗和工作人员的操作,炉内的三相电极位置不断发生变化。三相电极的较大相对位移会导致炉况波动,影响炉内的三相平衡度[2],产生严重的电能浪费,甚至可能引起电极事故。在该情况下,实现矿热炉三相电极位置检测对于及时调整电极、节能降耗、减少电极事故的产生具有重要意义。
由于矿热炉周边的工作环境存在高温、有害气体较多等问题[3],并且三相电极处于炉料内,三相电极位置的直接检测难以实现,工作人员在多数情况下只能根据电表变化和自身的经验判断三相电极位置。该方法的检测精度较低,对工作人员的能力和经验要求较高,并且难以实现节能降耗的要求。矿热炉电极通入三相交流电,经过炉料构成回路,在炉外将产生相应的磁场,并且随着电极的消耗和电极位置的移动,炉外磁场将发生变化。文献[1,4]中提出了一种磁场阵列检测法,对电极端部位置在内的关键参数进行精确检测,但存在系统体积较大、使用传感器数量较多等问题。文献[5]中用光电位移传感器实现矿热炉电极位置的非接触式检测,但该方法成本较高,并且炉外高温环境对该方法的检测精度影响较大。鉴于此,根据三相电极位置变化对炉外磁场的影响,找到合适的外磁场信号采样点,应用偏最小二乘(partial least squares,PLS)回归分析、径向基函数神经网络(radial basis function neural network,RBFNN)、粒子群优化RBFNN(particle swarm optimized RBFNN,PSO-RBFNN),设计了一种基于矿热炉外磁场信号的三相电极位置检测系统,为进一步调节三相电极位置和提高矿热炉生产效率提供理论依据。
1 矿热炉模型分析与样本集建立
结合COMSOL Multiphysics软件(COMSOL集团开发,简称COMSOL),构建了矿热炉仿真模型,该模型的主要结构如图1(a)所示。矿热炉仿真模型包括炉体、炉料、三相电极、空气环境等组成部分,其中炉料分为金属层、炉料层和炉渣层,如图1(a)所示。在建立几何结构后,对矿热炉各组成部分进行材料参数的设置和网格划分,并通过COMSOL中的AC/DC模块对矿热炉模型的磁场进行分析,磁场分析结果如图1(b)所示。
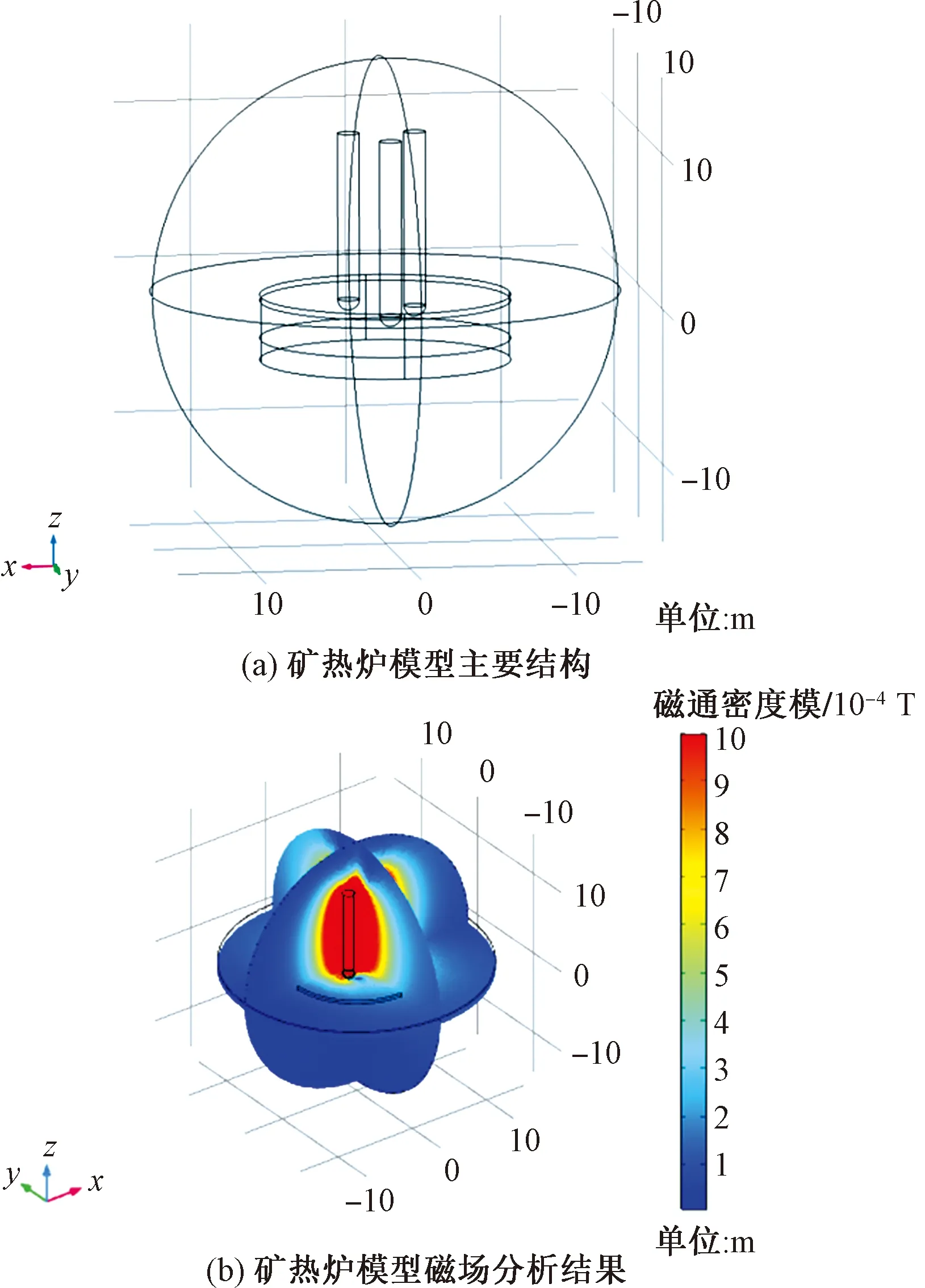
图1 矿热炉模型主要结构和磁场分析结果
根据图1(b)所示的磁场分析结果,使用COMSOL中的三维截线工具,结合文献[1,4]中矿热炉外磁场信号采样点的选取方法,进行如图2所示的三维截线的构建。根据图2所示的三维截线,分别提取截线所在位置的外磁场信号数据。其中图 2(b)使用圆形三维截线,并且为区分圆形截线的不同位置,将圆形截线按逆时针分为0~360°,起始点为截线和X轴正方向的交点。
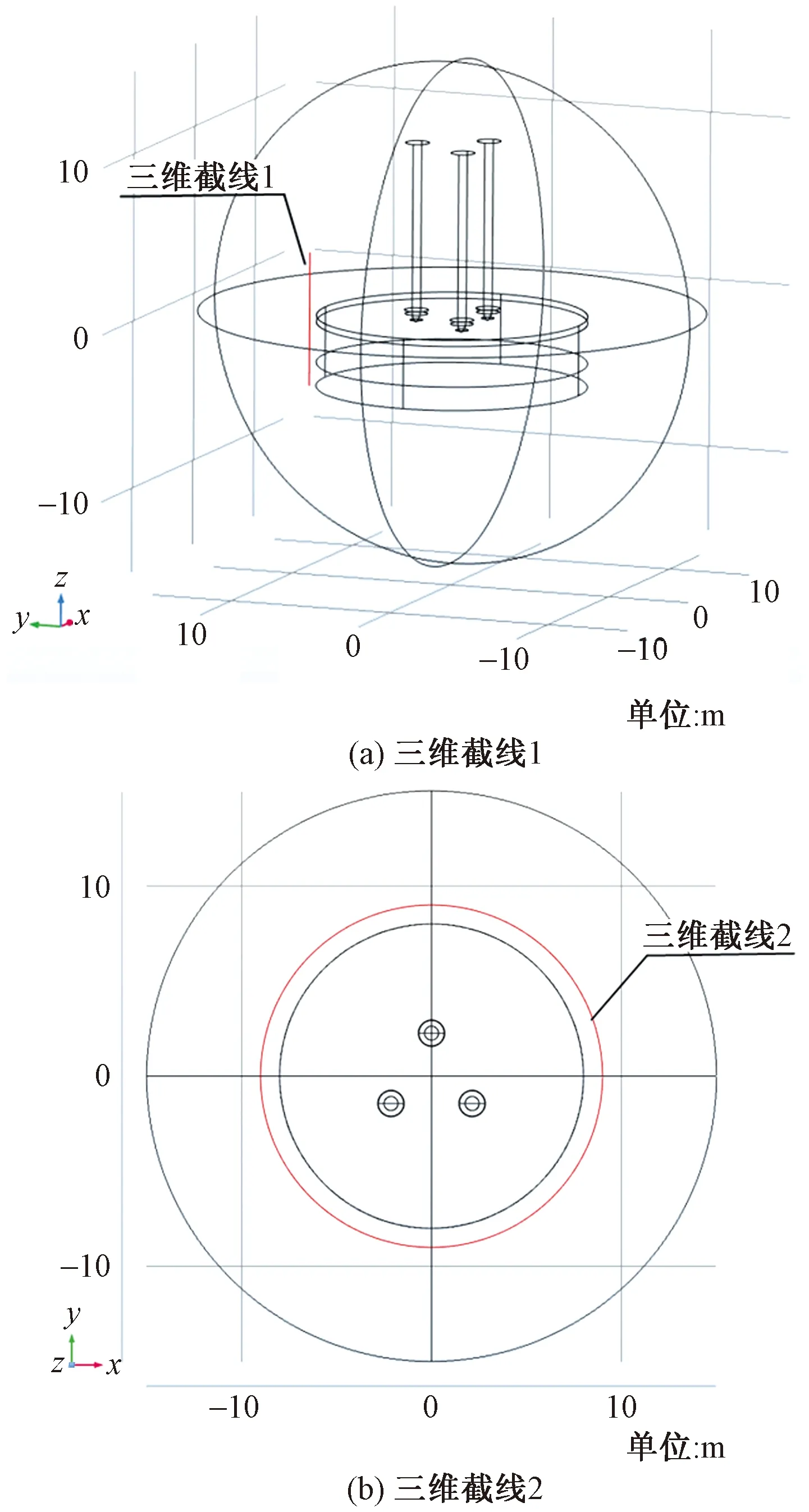
图2 在矿热炉模型中构建三维截线
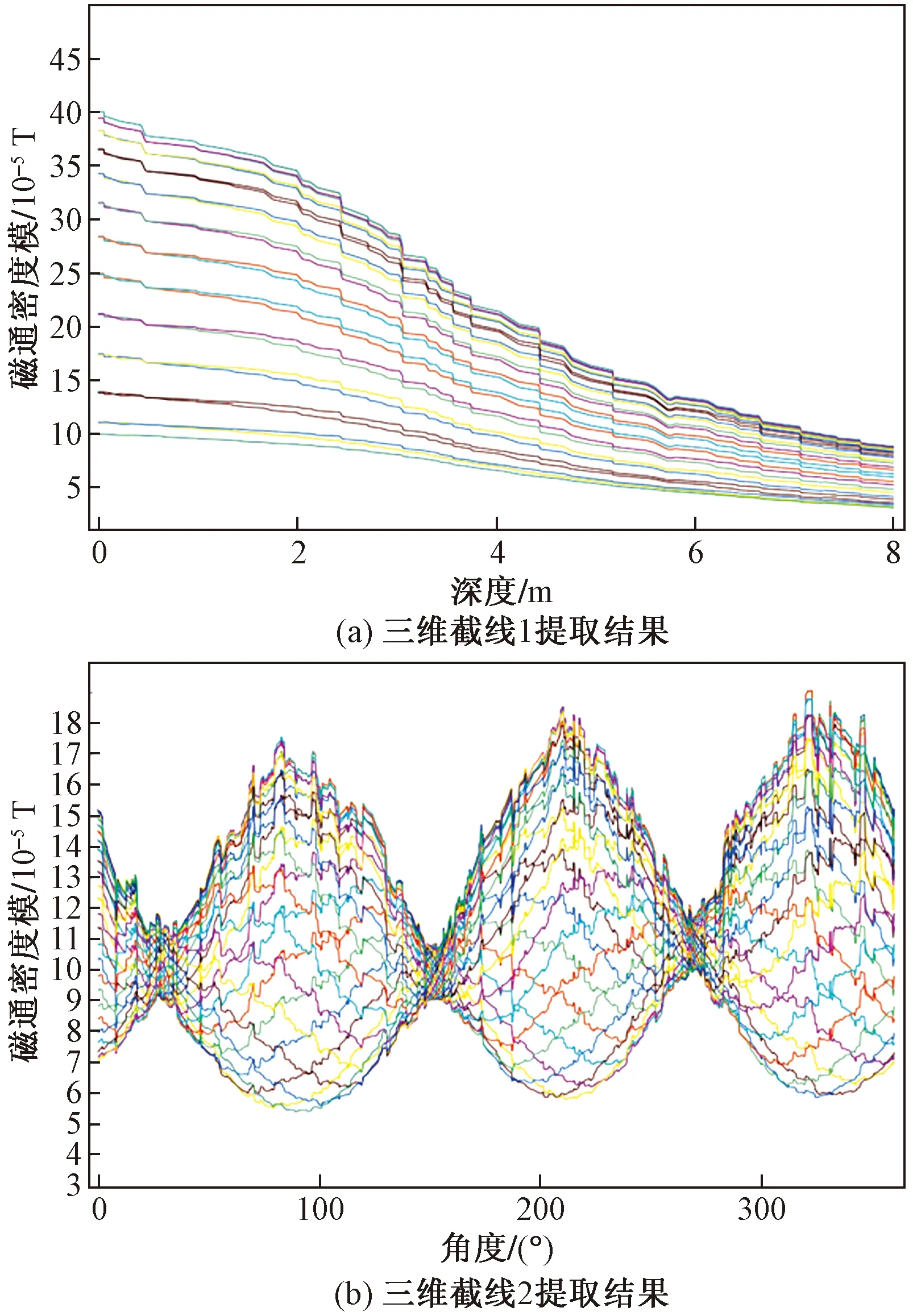
图3 三维截线提取的外磁场信号
通过三维截线(图2)提取的矿热炉外磁场信号如图3所示。在图3中,每条曲线表示一个周期内某个时间的外磁场信号。根据图3(a)显示的矿热炉外不同高度的磁场信号提取结果,可知中间区域磁信号变化较大,结合炉料分层情况、电极浸入深度范围[4],在中间区域设置四个采样层。为全面反映电极位置变化对矿热炉外磁场信号的影响,在炉体顶部和底部各设置一个采样层。图3(b)显示矿热炉外圆形三维截线不同角度的磁场信号提取结果。根据图3(b)显示的提取结果可知,90°、210°、330°的磁信号明显强于其他角度的磁信号。因此,在图3(a)确定的6个采样层中,分别选取这三个角度的位置作为矿热炉外磁场信号采样点。
根据确定的矿热炉外磁场信号采样点,使用随机函数调整矿热炉三相电极在炉中的浸入深度,生成70个具有不同电极位置的矿热炉模型,再分析不同电极位置情况下的矿热炉模型的外磁场信号。结合COMSOL后处理工具,对每一个模型都提取其在各采样点的磁场信号,建立机器学习的样本集,其中40个为训练集,30个为测试集。在此基础上,建立PLS回归分析、RBFNN、PSO-RBFNN这三种电极位置检测模型,并使用平均绝对误差、三相电极位置检测准确率、均方根误差对三种模型进行比较。
2 基于PLS的电极位置检测模型
根据对应于外磁场信号采样点的训练样本数据,对三相电极的具体位置进行PLS回归分析[6]。18个外磁场采样点的磁信号作为PLS的自变量X={x1,x2,…,x18},三相电极位置分别作为PLS的因变量Y={y1,y2,y3}。
对X={x1,x2,…,x18}和Y={y1,y2,y3}分别提取成分t1和u1,使得t1和u1之间的相关程度达到最大,并且尽可能多地代表原变量中的数据信息。在此基础上,进行X对t1、Y对u1的回归,并对回归方程精度进行判断。若未达到精度要求,则利用X和Y被t1、u1解释后的剩余信息进行t2和u2的提取,并依次类推,不断迭代,直到满足精度要求。如果最终提取了K个主成分,则在对X、Y进行回归后,建立的PLS回归方程如式(1)所示:
yk=αk1x1+αk2x2+…+αkpxp+Fk,k=1,2,…,q
(1)
式(1)中:αk1,αk2,…,αkp为回归系数;Fk为残差矩阵的第k列;q为因变量的个数。使用外磁场采样点的磁信号作为自变量,三相电极位置作为因变量,构造PLS回归分析模型,可得回归方程为
y1=-6.689 0+0.705 5x1+0.279 7x2+0.010 7x3+0.126 7x4-0.139 1x5+0.256 9x6+0.119 5x7+0.485 4x8+0.101 5x9-0.041 4x10+0.089 9x11+0.269 8x12-0.065 6x13+0.298 4x14+0.305 2x15-
0.334 3x16+1.394 3x17-0.282 8x18
(2)
y2=-5.841 8+0.169 8x1+0.012 3x2+0.391 3x3+0.109 0x4+0.007 0x5+0.400 4x6+0.096 4x7+0.043 4x8+0.392 3x9+0.079 5x10-0.013 5x11+0.420 0x12+0.047 3x13+0.012 7x14+0.448 3x15-
0.013 6x16+0.242 5x17+0.376 0x18
(3)
y3=-4.816 3+0.287 6x1+0.023 1x2+0.037 5x3+0.408 6x4+0.184 2x5-0.008 7x6+0.399 4x7+0.022 0x8+0.012 6x9+0.468 4x10+0.123 7x11-0.029 2x12+0.486 0x13+0.046 8x14-0.017 5x15+
0.548 6x16-0.178 9x17+0.098 3x18
(4)
式中:y1、y2、y3分别为矿热炉A、B、C三相的电极位置,x1,x2,…,x18为矿热炉外1~6层共18个不同采样点的磁感应强度。
通过已建立的训练集和测试集中的样本数据,对PLS回归分析模型进行测试,可得本模型的三相电极位置平均绝对误差为0.096 7(训练集)、0.125 9(测试集)、平均检测准确率为89.57%(训练集)、87.21%(测试集),均方根误差为0.121 2(训练集)、0.157 1(测试集)。PLS模型对训练集和测试集的检测结果如图4所示。
由图4和平均绝对误差、平均检测准确率、均方根误差这3种主要的检测指标可知,PLS模型能够有效实现对矿热炉三相电极位置的检测,当三相电极位置相差较大或存在处于临界位置的电极时,存在一定检测误差,总体上具有较好的三相电极位置检测效果。
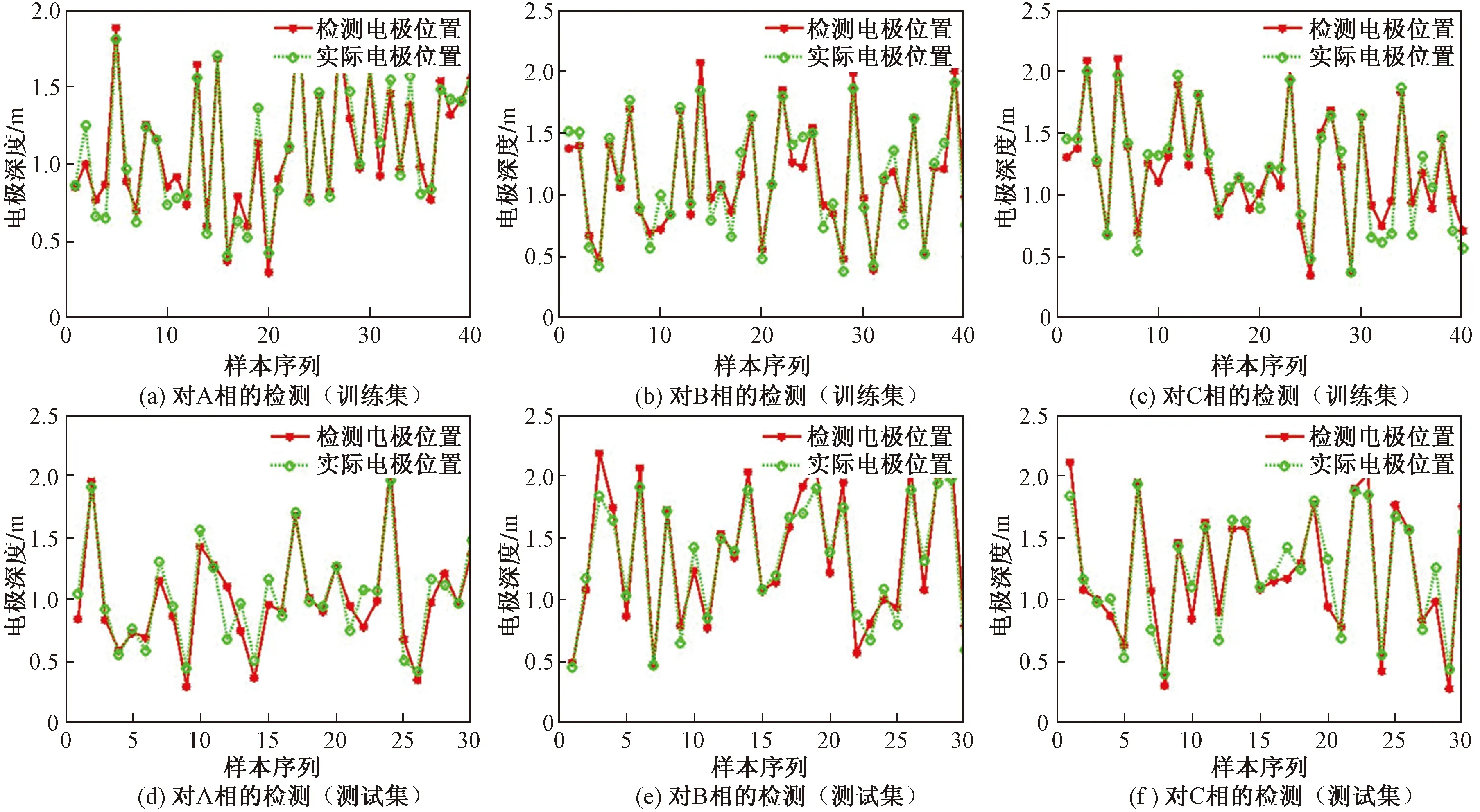
图4 PLS模型对训练集和测试集的检测结果
3 基于RBFNN的电极位置检测模型
使用三相电极位置样本集(训练集和测试集),建立基于RBFNN[7]的三相电极位置检测模型。
将第1节中选取的18个外磁场信号采样点的磁感应强度作为输入,将矿热炉三相电极位置作为输出,根据优化结果可得隐含层节点数为30。使用高斯函数作为网络的激活函数,结合K均值聚类算法确定RBF中心位置,并根据最小二乘法得到神经网络的连接权值。
使用三相电极位置样本集(训练集包括40个样本,测试集包括30个样本)对RBFNN进行训练,最终建立基于RBFNN的三相电极位置检测模型。模型对训练集和测试集的检测结果如图5所示。
模型的三相电极位置平均绝对误差为0.094 9(训练集)、0.123 7(测试集),平均检测准确率为89.31%(训练集)、86.62%(测试集),均方根误差为0.120 9(训练集)、0.150 4(测试集)。该模型在平均绝对误差、均方根误差这两个评价指标上均优于PLS模型,在平均检测准确率指标上与PLS模型相近,总体上性能优于PLS模型,能更精确地实现对矿热炉电极位置的检测。
4 基于PSO-RBFNN的电极位置检测模型
考虑到一般RBFNN在确定网络参数等方面存在的问题,使用粒子群算法(PSO)的全局寻优能力[8]对RBFNN进行优化,获得最优的网络参数,构建基于PSO-RBFNN的三相电极位置检测模型。

图5 RBF模型对训练集和测试集的检测结果
PSO算法是通过粒子群中每个粒子的不断迭代更新自身的速度和位置来获得粒子的个体极值和全局极值[9]。将粒子群的每一个粒子都对应一种RBF神经网络参数,粒子的适应度值由训练集40个样本的均方根误差表示,即均方根误差较小的粒子,对应的适应度较好。使用PSO算法对RBFNN进行优化的主要流程如下所示。
(1)根据三相电极位置检测模型的输入和输出要求,对RBFNN进行初始化,获得中心位置、权值、偏置等初始网络参数。
(2)设置粒子群算法的相关参数,包括粒子个数N,学习率c1、c2,最大迭代次数kmax,粒子最大速度vmax等。
(3)根据初始网络参数和粒子群相关参数,结合随机数,生成对应于各类网络参数组合的粒子。
(4)计算各粒子的适应度,根据适应度,获取粒子的个体最优和全局最优。
(5)对粒子进行更新,并重新计算适应度,与之前的适应度最优粒子进行比较,得到新的个体最优和全局最优。
(6)对当前的迭代次数和适应度进行判断,若达到最大迭代次数kmax或达到设定的适应度,则停止迭代,否则继续迭代优化。
(7)当迭代结束时,使用最优粒子对应的网络参数构建RBFNN模型,检测三相电极位置。
PSO算法优化RBFNN,建立三相电极位置检测模型的主要流程如图6所示。
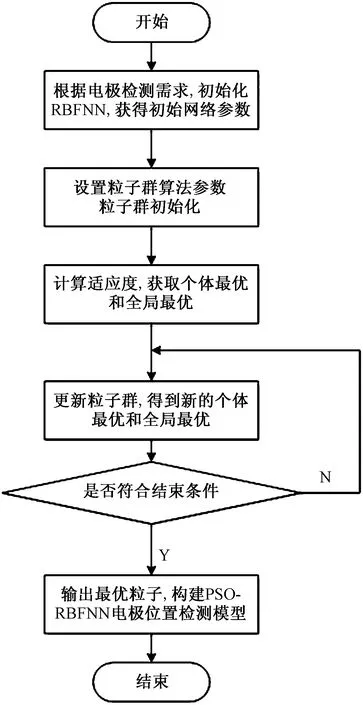
图6 PSO优化RBF神经网络流程图
根据PSO算法优化的RBFNN,将矿热炉外18个采样点的磁感应强度作为输入,三相电极位置作为输出,取粒子个数N=20,学习率c1=c2=2,最大迭代次数kmax=500,结合训练集的样本数据,建立基于PSO-RBFNN的三相电极位置检测模型。本模型对训练集和测试集的检测结果如图7所示。
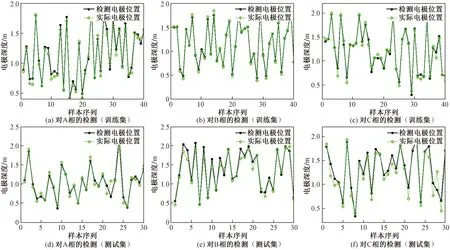
图7 PSO-RBF模型对训练集、测试集的检测结果
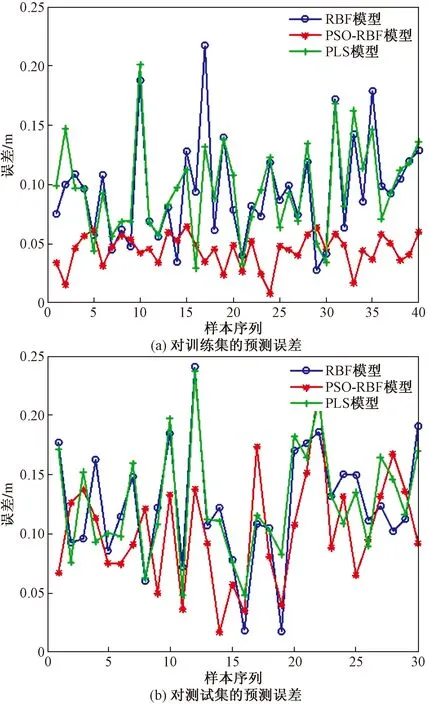
图8 不同电极位置检测模型的预测误差比较
结合图7和计算结果可知,模型的三相电极位置平均绝对误差为0.044 3(训练集)、0.101 5(测试集),平均检测准确率为94.98%(训练集)、90.21%(测试集),均方根误差为0.053 5(训练集)、0.131 1(测试集)。PSO-RBF模型的平均绝对误差(训练集)、平均检测准确率(训练集)和均方根误差(训练集)都远优于PLS模型和RBF模型,具有优越的非线性拟合能力。在平均绝对误差(测试集)、平均检测准确率(测试集)、均方根误差(测试集)上也优于另外两个模型,对三相电极位置的预测准确率较高。在图8中对三种电极位置检测模型的预测误差进行具体对比。
图8分别为三种电极位置检测模型的训练集、测试集误差对比图,对训练集或测试集中同一样本三相电极位置预测误差绝对值取平均值,作为该样本的预测误差,并通过红线、蓝线和绿线分别表示PSO-RBF模型、RBF模型和PLS模型的预测误差。
由图8和3个主要评价指标的计算结果可知,PSO-RBF模型和RBF模型在整体性能上优于PLS模型,能够较好地依据外磁场信号实现对矿热炉三相电极位置的检测。
在两种神经网络模型中,PSO-RBFNN的性能更加优越,在三个主要评价指标(平均检测准确率、平均绝对误差和均方根误差)上优于RBF模型,特别是在平均绝对误差(训练集)和平均检测准确率(训练集、测试集)等方面,PSO-RBF模型远优于另两种模型,具有优越的非线性拟合能力,能够较精确地实现对矿热炉三相电极的检测。
5 三相电极位置检测系统GUI设计
考虑到矿热炉三相电极位置检测系统实际使用的需要,在MATLAB图形用户界面[10]开发环境下,构建三相电极位置检测系统GUI,将上述建立的PLS模型、RBF模型和PSO-RBF模型引入该平台,作为检测系统的上位机[11]。
在实际检测中,系统提供两种磁信号读取方式,可以选择自动读取(通过串口与下位机通信获得外磁场信号),或者选择手动输入,并在GUI中显示不同采样点的磁信号数据。系统将三个不同的检测模型集成到同一应用界面,适应不同检测情况选择检测模型,在选择检测模型后,可对矿热炉三相电极位置进行检测。系统还提供数据保存功能,能够及时保存检测结果、显示保存路径,用于进一步的分析和比较。三相电极位置检测系统GUI如图9所示。
图9选用PLS模型作为检测模型,选择RBF模型和PSO-RBF模型作为检测模型,对同一样本的检测结果如图10所示。
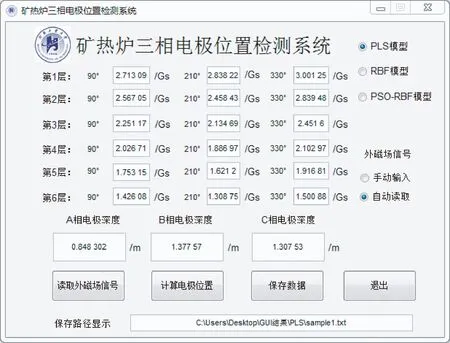
图9 矿热炉三相电极位置检测系统GUI
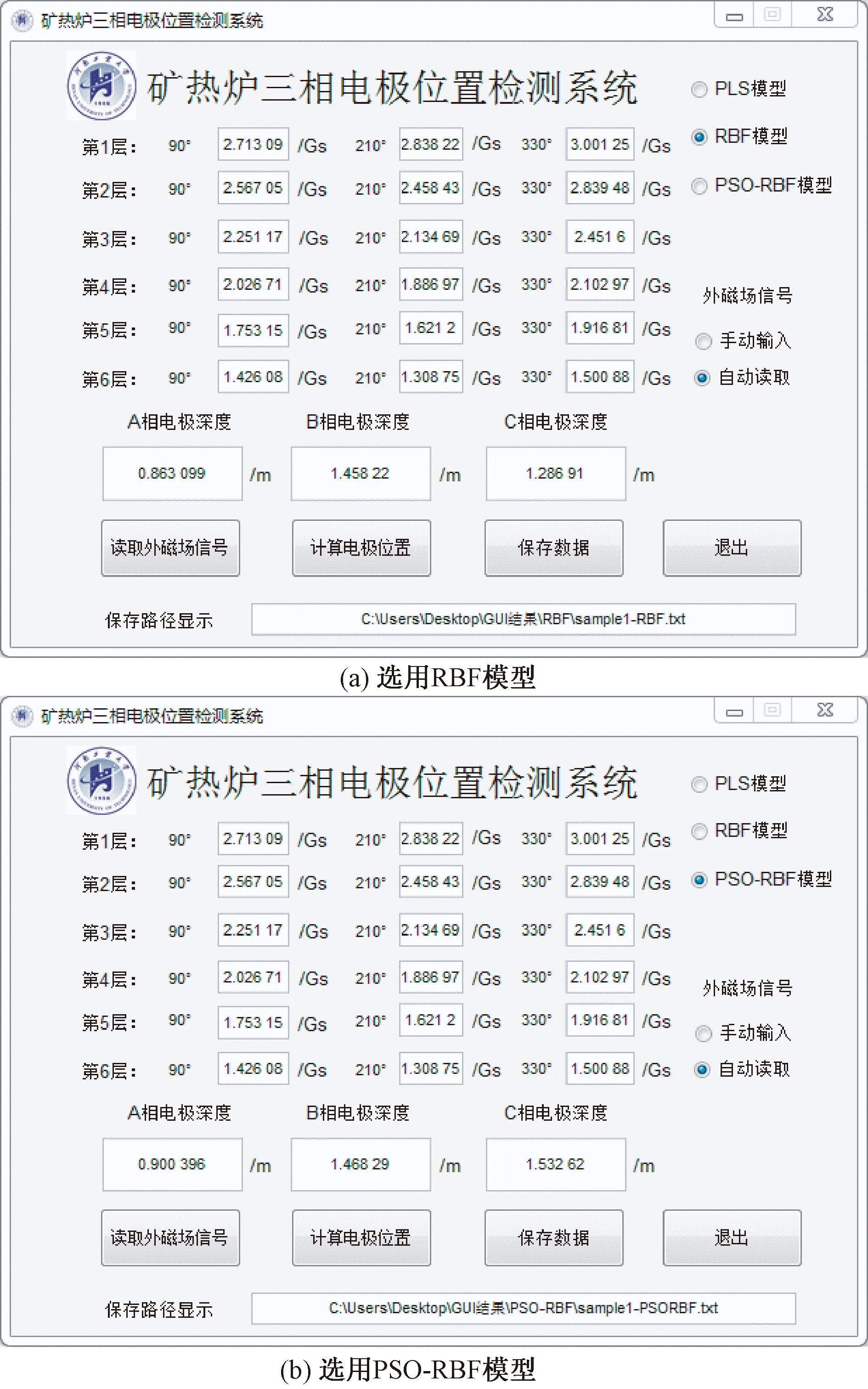
图10 GUI选用RBF、PSO-RBF模型的检测结果
6 结论
根据矿热炉三相电极位置精确、安全检测的实际需求,设计了一种基于矿热炉外磁场信号、非接触式的三相电极位置检测系统。首先根据矿热炉电路和几何构造,建立了矿热炉仿真模型,并对矿热炉电场、外磁场进行分析和计算,选取矿热炉外磁场信号采样点。在选取的采样点,对不同的矿热炉模型进行外磁场信号提取,建立矿热炉外磁场信号样本集。在此基础上,建立了三种基于矿热炉外磁场信号的三相电极位置检测模型(PLS模型、RBF模型和PSO-RBF模型),通过多种评价指标的分析和比较,这三种模型都能实现对矿热炉三相电极位置的精确检测,其中PSO-RBF模型的整体性能最优,为矿热炉各类参数测量和生产过程监控提供依据,具有较好的实际应用潜力。
