融合AR模型和MCMC方法的水文模拟不确定性分析

贺新月,曾献奎,王 栋

(南京大学地球科学与工程学院,江苏 南京 210023)

不确定性表示由于缺乏足够信息而未能准确描述或预测某事件的状态,其广泛存在于工程、金融、地球科学等多个领域[1]。近几十年来,流域水文过程的模拟预测及其不确定性分析已经成为水文领域的研究热点之一[2-3]。

水文系统的复杂性、资料的缺乏及人类认识的局限性等原因使水文模型参数存在较大的不确定性[4]。随着抽样算法的不断提升,马尔可夫链蒙特卡洛(MCMC)模拟方法被广泛用于分析复杂、高维的水文模型参数不确定性问题。Panday等[5]采用MCMC方法对喜马拉雅地区Tamor河流域的融雪径流模型进行参数识别,结果表明MCMC方法可减少模型参数的不确定性,提高模型预测性能。鲁帆等[6]以汉江流域丹江口水库为例,将水文频率分布线型的未知参数看作随机变量,采用MCMC方法估计未知参数和设计洪水的后验分布,结果表明MCMC模拟可有效推算出水文频率分布线型参数及设计洪量的后验分布。

MCMC方法通过似然函数描述模拟值与观测值的拟合程度,确定模型参数的接受概率。在传统的MCMC模拟中,通常假设模型模拟值与观测值的差值(模拟残差)无自相关性,将似然函数中的残差协方差矩阵简化为对角型结构。Lu等[7]在采用最大似然估计法识别铀反应运移柱体实验模型参数的研究中,发现模拟残差时间序列(残差序列)存在显著的自相关性,采用简化的残差协方差矩阵计算似然函数,将对模型表现的合理评价产生影响。Pang[8]为分析二元时间序列随时间的动态变化情况,提出一种基于AR模型的线性多级模型来模拟该时间序列,通过修正传统MCMC方法中的残差协方差矩阵,有效识别模型参数。

本研究将融合AR模型的改进MCMC方法(AR-MCMC)应用于水文模拟的不确定性分析中,并以新疆提孜那甫河流域的融雪径流模拟为例,对比评价传统MCMC和AR-MCMC方法进行参数不确定性分析的表现。

1 方 法

1.1 MCMC模拟

马尔可夫链蒙特卡洛(MCMC)模拟方法通过构建平稳分布的马尔可夫链搜索模型参数的概率分布空间[9]。在搜索过程中,不断融合观测信息D计算似然函数,定量评价模型在参数θ下对观测数据D的拟合表现,使得马尔可夫链从模型参数θ的先验分布逐渐收敛至其后验分布[10]。在MCMC模拟中一般采用式(1)计算似然函数。

(1)

式中:L(θ|D)——参数θ的高斯似然函数;N——观测数据的数量;f(θ)——参数取为θ时的模型输出值;Σ——模拟残差协方差矩阵。

MCMC模拟的一般步骤如下[11]:(a) 根据经验设置模型参数θ[θ1,θ2, …,θd]的先验分布,d表示模型参数维数。(b) 基于某种分布函数在参数θ的先验分布范围内抽取样本θi(i=1,…,M),其中M为马尔可夫链长度;运行模型,计算参数样本θi的L(θi|D)。(c) 对比L(θi|D)与上一步马尔可夫链样本θi-1的L(θi-1|D),计算θi的接受概率,更新马尔可夫链。(d) 根据当前所有样本信息更新步骤(b)中的样本抽取算法。(e) 重复步骤(b)～(d)至马尔可夫链达到收敛标准,将获得的马尔可夫链样本θi和f(θi) 统计得到模型参数θ与模拟结果f(θ)的后验分布。当前,有多种抽样算法可实现步骤(b)～(d),本文采用DREAMZS算法[12],该算法适用于复杂条件下的高维参数识别与不确定性分析。

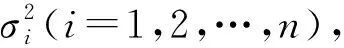
1.2 AR模型

AR模型是一种被广泛用于刻画时间序列X(X1,X2,X3,…,Xn)自相关性的线性回归模型。利用AR模型分析时间序列的相关性,需估算该序列的自相关函数值(ρ)与偏相关函数值(k)[14]。其中ρ表示序列中2个变量之间的总相关性,k表示2个变量排除了其他中间变量影响后的相关性。

根据k的衰减情况可确定AR模型的阶数P[15]。若k在i个时间间隔后开始稳定在(-2/n0.5, 2/n0.5)范围内,则序列的自回归阶数P为i。确定模型阶数P后,可依据式(2)计算第i个与第j个变量的自相关系数cij,其取值仅与i、j变量的时间间隔|i-j|有关,可定义为时间间隔l的函数g(l)。

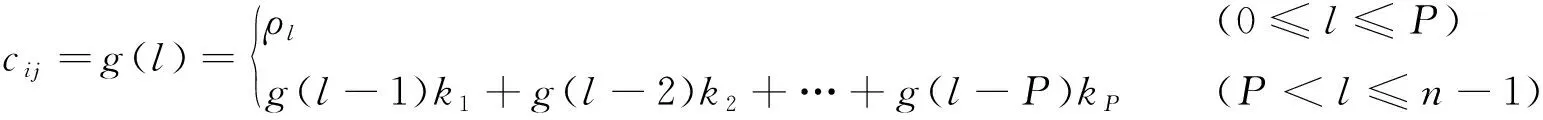
(2)

1.3 AR-MCMC方法

融合AR模型与MCMC方法的不确定性分析方法(AR-MCMC),采用AR模型描述残差序列rN的相关性,修正MCMC似然函数中的残差协方差矩阵。其具体步骤如下:(a) 构建水文模型,运行传统MCMC进行参数不确定性分析;(b) 计算似然函数最大时模拟残差序列的ρ与k,确定自回归阶数P;(c) 重新运行MCMC,针对每次迭代中的模拟残差序列,建立其AR模型,修正残差协方差矩阵结构为Cek并计算似然函数L(θ|D),更新马尔可夫链至总链长为M;(d) 对比传统MCMC及AR-MCMC方法的不确定分析结果。

步骤(c)中,Cek的计算公式如下:

Cov(i,j)=E(ri-E(ri))E(rj-E(rj))=cijσiσj

(3)

式中Cov(i,j)——Cek中i行j列位置处的元素,表示残差序列中第i个与第j个残差之间的协方差;ri、rj——i时刻和j时刻的残差(i,j=1,2,…,N);σi、σj——i时刻和j时刻观测误差的标准差。

1.4 模型评价方法

选择模型边缘似然值、预测区间的性质以及对观测序列的拟合精度来评价水文模型在传统MCMC和AR-MCMC方法进行不确定性分析的表现。边缘似然值(L0)表示似然函数在先验概率分布下的期望,可用于评价模型表现或估计模型权重[16]。预测区间性质的评价指标包括区间平均宽度W、对观测数据的覆盖率R、区间对称性系数S。似然函数最大值对应的纳什系数E可用于评价模型对观测序列的拟合精度。以上各项评价指标计算公式如下:

(4)

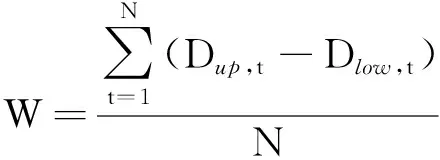
(5)

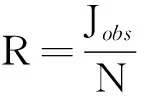
(6)

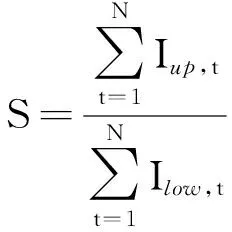
(7)

(8)

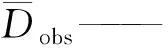
本文选择95%置信水平下的分布区间(2.5%～97.5%)作为预测区间。L0越大说明模型表现越好,S越接近1表明区间对称性越好,E越大说明模型模拟序列与实测序列拟合效果越好。

2 案 例 研 究

2.1 研究区概况

研究区位于新疆提孜那甫河流域,流域地形复杂,海拔跨度1 472～6 352 m,面积约为5 518 km2。区域内气温年内变化大,蒸发强烈,降水稀少,但冰雪资源丰富,冰雪融水是河流的主要补给来源。研究对象为区域内融雪及降水形成的地表径流。

2.2 SRM模型

SRM模型是一种经验性融雪径流模型,将径流量分为3个部分:融雪径流、降雨径流以及原始径流衰减后的径流,模型基本结构如下[17]:

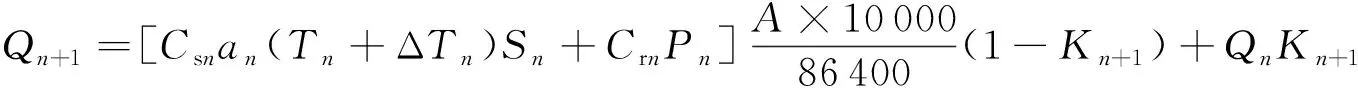
(9)

式中:Q——日径流量,m3/s;Cs——融雪径流系数;Cr——降水径流系数;a——度日因子,表示单位温度、单位时间的融雪深度,cm/(℃·d);T——度日数,℃·d;ΔT——利用温度直减率对度日数进行的校正值,℃;S——积雪覆盖率;P——降雨形成的径流深,cm;A——流域或流域分区的面积,km2;K——退水系数;10 000/86 400——单位换算系数。其余符号含义见文献[18]。

本次研究中,需要识别的模型参数包括a、Cs、Cr、K的拟合参数x和y。

2.3 数据

研究区高程数据采用NASA(national aeronautics and space administration)的ASTER数据库的DEM数据。气温数据通过测站温度和全球平均温度直减率 (0.65℃/100 m)推求获得。降水数据采用TRMM(tropical rainfall measuring mission)卫星产品。另外利用MODIS(moderate-resolution imaging spectrometer) 8 d积雪合成产品(MOD10A2, h24v25) 进行线性插值得到每日积雪覆盖率。径流数据来自研究区内的水文观测站——玉孜门勒克站。此次研究将2006年1月1日至12月31日的径流观测数据用于模型识别,2007年1月1日至12月31日的径流观测数据用于模型验证。

3 结果与讨论

3.1 残差序列的P值

根据步骤中残差序列ρ与k的计算结果,绘制两者的变化曲线(图1)。由图1可见:ρ值在时间间隔为1 d时接近0.75,之后随着时间间隔的增加呈现单边递减趋势,最终接近0,说明模拟残差序列具有显著的自相关性,序列中2个残差变量之间为正相关关系,并且这种正相关关系随着时间间隔的增加逐渐减弱;根据AR模型计算得到k的截尾置信区间为(-0.105,0.105),结合k变化曲线可知,时间间隔大于1 d时k值稳定在其截尾置信区间内,故此次研究实例中残差序列的自回归阶数P为1。

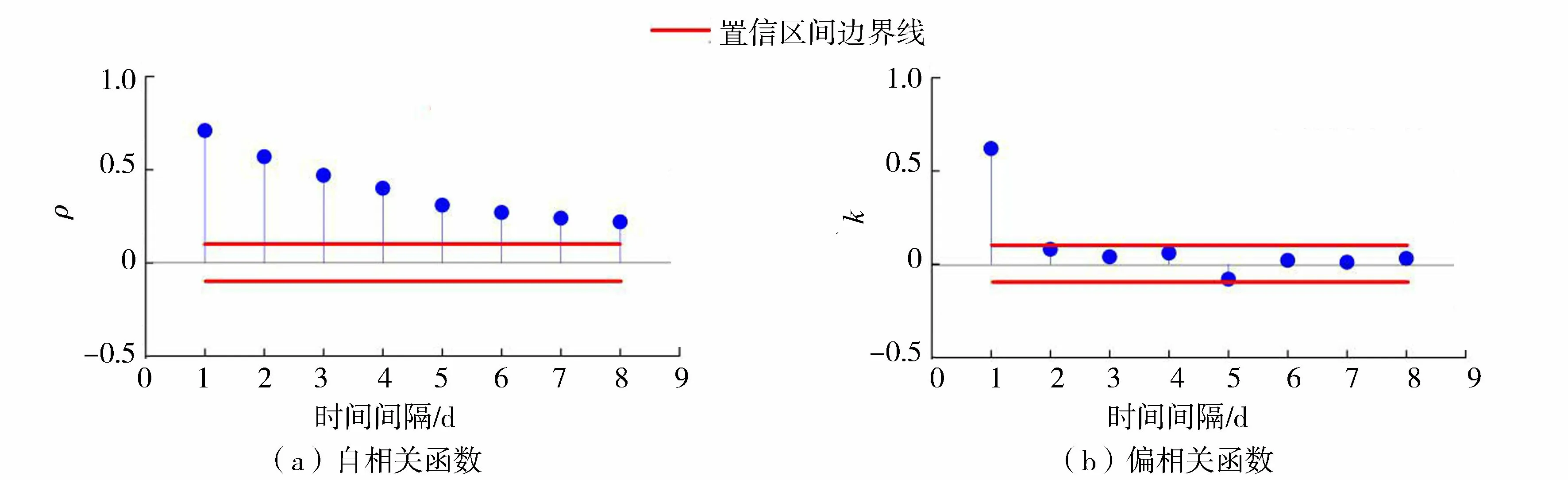
图1 残差ρ与k变化曲线Fig.1 Variation curves of residuals’ ρ and k

3.2 模型参数识别

本次研究中需要识别的SRM模型未知参数包含x、y、Cs、Cr、a,各参数的先验分布范围依次为(0.85,1.2)、(-0.15, 0.3)、(0.1, 0.6)、(0.1, 0.6)、(0.05, 0.5)。根据模拟结果统计各参数经MCMC方法与AR-MCMC方法识别后的后验概率密度分布如图2所示,似然函数最大值对应的SRM参数取值如表1所示。采用MCMC与AR-MCMC进行SRM模拟时,获得的参数y和Cr后验分布(如分布范围、形状)比较相似,而参数x、Cs和a的后验分布差别较大。因此,MCMC与AR-MCMC方法采用不同结构的残差协方差矩阵计算似然函数,导致2种方法获得的参数识别结果不一致。

图2 基于传统MCMC和AR-MCMC的SRM参数后验分布Fig.2 Posterior distributions of SRM parameters based on MCMC and AR-MCMC

表1 似然函数最大值对应的模型参数值

表2 基于MCMC与AR-MCMC的识别与验证结果

Table 2 Calibration and verification results based on MCMC and AR-MCMC

3.3 模型评价结果

采用不同结构的残差协方差矩阵(Cε不考虑残差序列自相关性、Cek考虑残差序列自相关性)计算的边缘似然值L0如图3所示。由图3知:2种结构的残差协方差矩阵对应的边缘似然值均随着样本数的增多逐渐收敛,但Cek对应的边缘似然值更大。因此,在AR-MCMC模拟过程中采用Cek计算似然函数,能获得更大的边缘似然值,即模型表现更好[18]。

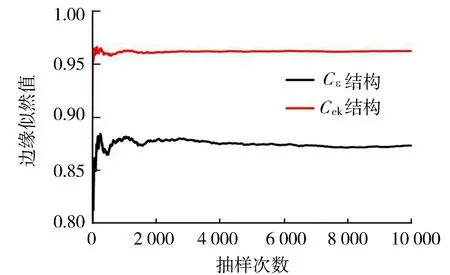
图3 不同残差协方差矩阵对应的边缘似然值Fig.3 Marginal likelihoods for different residual covariance matrixes

根据MCMC与AR-MCMC 方法进行SRM模型不确定性分析的径流量模拟结果,各项评价指标的计算结果见表2,融雪径流预测区间绘图见图4。结合图表分析:在识别期,AR-MCMC方法比MCMC方法获得的流量预测区间平均宽度更大,分别为18.67 m3/s和12.31 m3/s;预测区间对实测数据的覆盖率更高,分别为74.79%和59.73%;预测区间对称性表现更好,对称性系数分别为0.87和0.66。验证期MCMC方法和AR-MCMC方法的评价结果与识别期一致,因此AR-MCMC方法较MCMC方法能推求出性质更优的预测区间。另外,采用传统MCMC方法进行SRM模拟时,识别期与模拟期的纳什效率系数分别为0.84、0.87。而采用AR-MCMC方法对应识别期与模拟期的纳什效率系数分别为0.86、0.89。由此可见,采用AR-MCMC方法进行融雪径流模拟具有更优的拟合效果。

图4 基于传统MCMC方法和AR-MCMC方法的SRM在识别期与验证期的径流模拟表现Fig.4 Runoff simulation performances of SRM based on traditional MCMC and AR-MCMC during calibration and verification periods

综上,采用AR-MCMC方法进行SRM模拟时,通过考虑残差序列之间的相关关系,改进似然函数中的残差协方差矩阵,更新计算似然函数,能够更好地进行模型参数不确定性分析。因此,AR-MCMC方法能够更好地对研究区融雪径流过程进行模拟预测。

4 结 语

在传统的水文模型不确定性分析中通常忽略模拟残差序列的自相关性,将似然函数中的残差协方差矩阵简化为对角型结构,因此可通过修正残差协方差矩阵进一步提高模型不确定性分析效果。本文将融合AR模型的MCMC方法(即AR-MCMC方法)应用于水文模型不确定性分析中,利用AR模型刻画水文模型残差序列的自相关性,修正残差协方差矩阵,更新计算MCMC方法中的似然函数。

通过新疆提孜那甫河流域融雪径流模拟的案例研究,分别利用传统MCMC方法与AR-MCMC方法进行融雪径流模拟及预测的不确定性分析,结果发现,SRM模拟的残差序列具有显著的自相关性,其对应的自回归阶数P为1。采用AR模型修正似然函数中残差协方差矩阵后,得到了更大的模型边缘似然值,即提高了模型表现。此外,与传统MCMC方法相比,利用AR-MCMC方法进行SRM模拟及不确定性分析所获得的径流量预测区间对观测数据的包含率更高、区间对称性更好,似然函数最大值对应模型的融雪径流拟合效果更好。