线性广义系统P型迭代学习控制在Lp范数意义下的收敛性
2020-04-22张克军刘万利
张克军, 刘 芳, 刘万利
(徐州工程学院数理学院,徐州 221018)
广义系统[1]又称为奇异系统,是客观系统自然表示的一种,可以更好地刻画描述客观系统的性能特征,与正常系统相比,其形式更具广泛性。自20世纪70年代广义系统被提出以来,其理论不断完善、发展,在航空航天、能源、石油、化工和通信等诸多领域被广泛应用,这使得广义系统及其理论的研究深受许多学者的青睐。
迭代学习控制[2]是智能控制的重要分支之一,适用于具有重复运行性质的动力学系统,在不依赖系统精确模型的情况下,就可实现对期望输出的精确跟踪。然而,现有的关于迭代学习控制的理论和应用研究主要是针对常义系统的。与之相比,由于广义系统存在脉冲项,对广义系统的迭代学习控制进行研究要困难得多,相关研究成果也逊色不少。采用分块矩阵的思想,在对线性广义系统进行奇异值分解后,文献[3]提出了一种新的控制算法,并对算法的收敛性进行了理论分析。借助矩阵理论和不等式技巧,文献[4-5]分别讨论了线性广义系统在四种类型迭代学习控制算法下的收敛性问题。针对带控制时滞广义系统和单个状态时滞的广义系统,结合矩阵广义逆理论,文献[6-7]分别讨论了PID型、闭环PD型迭代学习算法收敛条件。文献[8]提出了一类广义系统的二阶迭代学习控制算法,并借助Qp因子讨论了算法的收敛速度问题。文献[9]研究了一类线性广义系统在固定初值下的闭环PD型和D型迭代学习控制算法的收敛条件,并对算法的收敛性进行了证明。针对一类线性广义系统,文献[10]研究了一种带指数变增益的闭环D型学习算法的收敛性。一些学者对离散广义系统也有研究,例如:文献[11]对一类离散广义系统的PD型迭代学习控制算法的跟踪问题进行了讨论,此类研究还有文献[12];此外,在离散频域中,针对一类连续线性广义系统,文献[13]讨论了P型迭代学习控制算法的收敛性态问题。
在理论分析过程中,在度量跟踪误差时,上述文献主要采用λ范数。但是,当参数λ取值比较大时,虽然能够满足控制算法的收敛条件,但在系统重复运行时,暂态跟踪误差的最大值落在实际工程应用的容许范围之外,导致系统崩溃[14-15]。在文献[16-17]中,阮小娥等利用Lebesgue-p(Lp)范数研究了线性时不变系统P型和PD型迭代学习控制算法的收敛性,发现系统的收敛条件不依赖参数λ的取值,主要取决于系统本身属性和学习增益矩阵。进一步,在Lp范数意义下,文献[18-20]讨论了分数阶线性系统的分数阶迭代学习控制算法的收敛性问题。受此启发,在对线性广义系统进行非奇异变换的基础上,利用Lp范数对一、二阶P型迭代学习控制算法的收敛条件进行分析;然后,利用Qp因子方法对两种控制算法的收敛速度进行对比,并通过仿真实验验证理论的正确性。
1 数学知识
下面列出理论分析需要的一些相关数学知识。
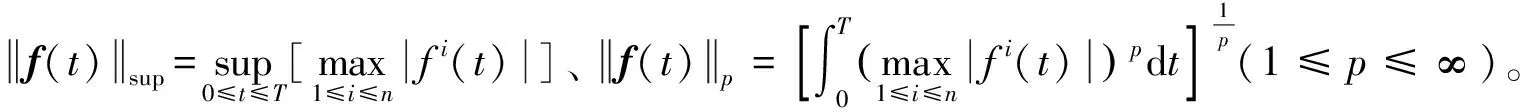
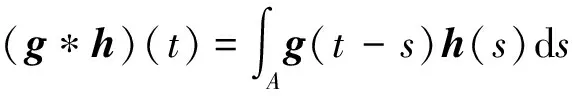
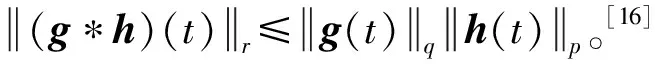
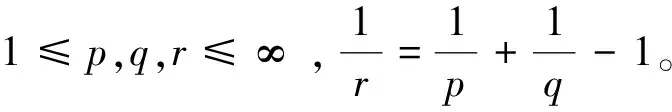
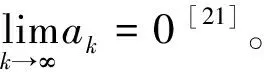
2 问题描述及分析
考虑如下连续线性广义系统:
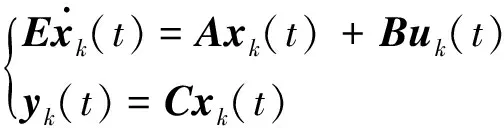
(1)
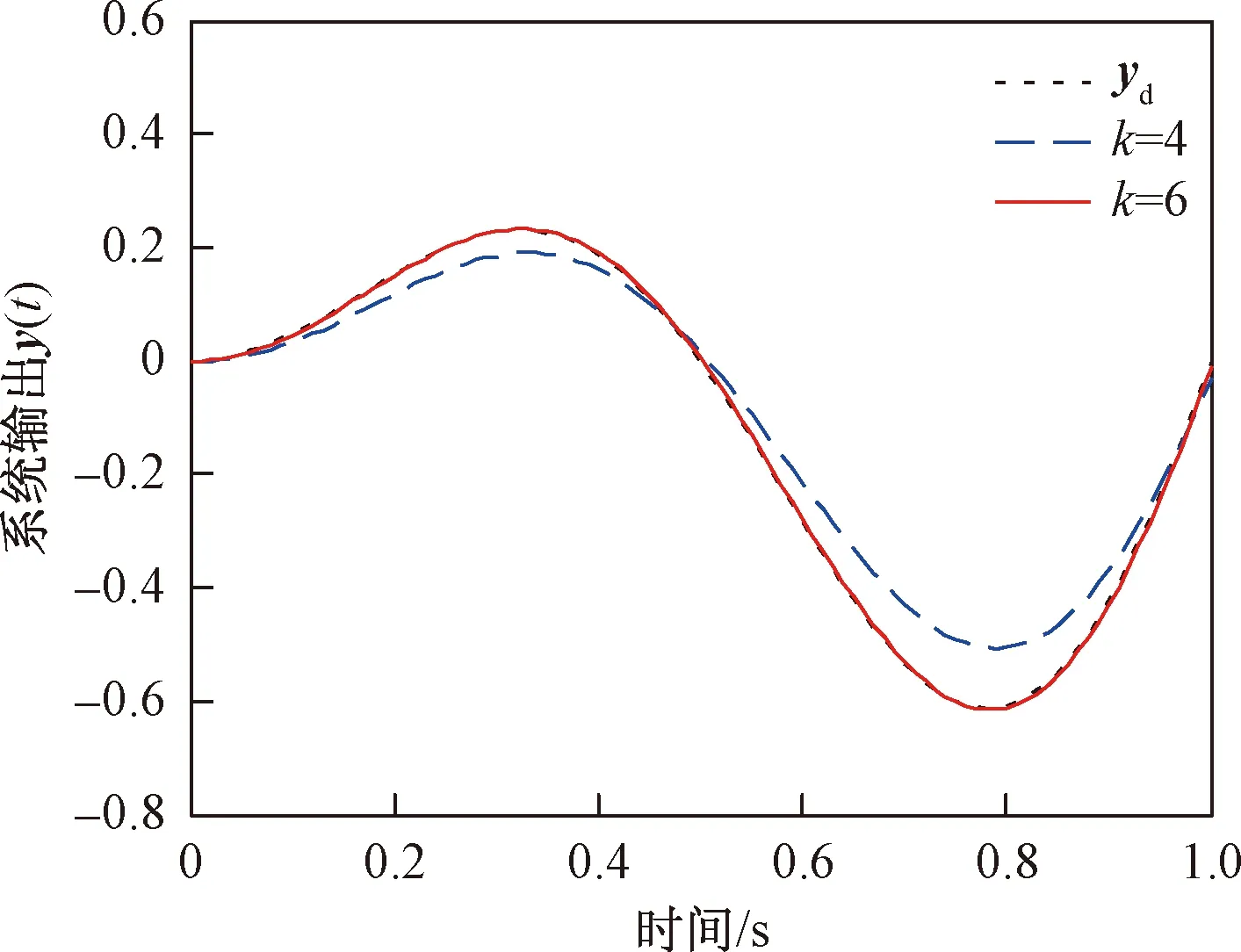
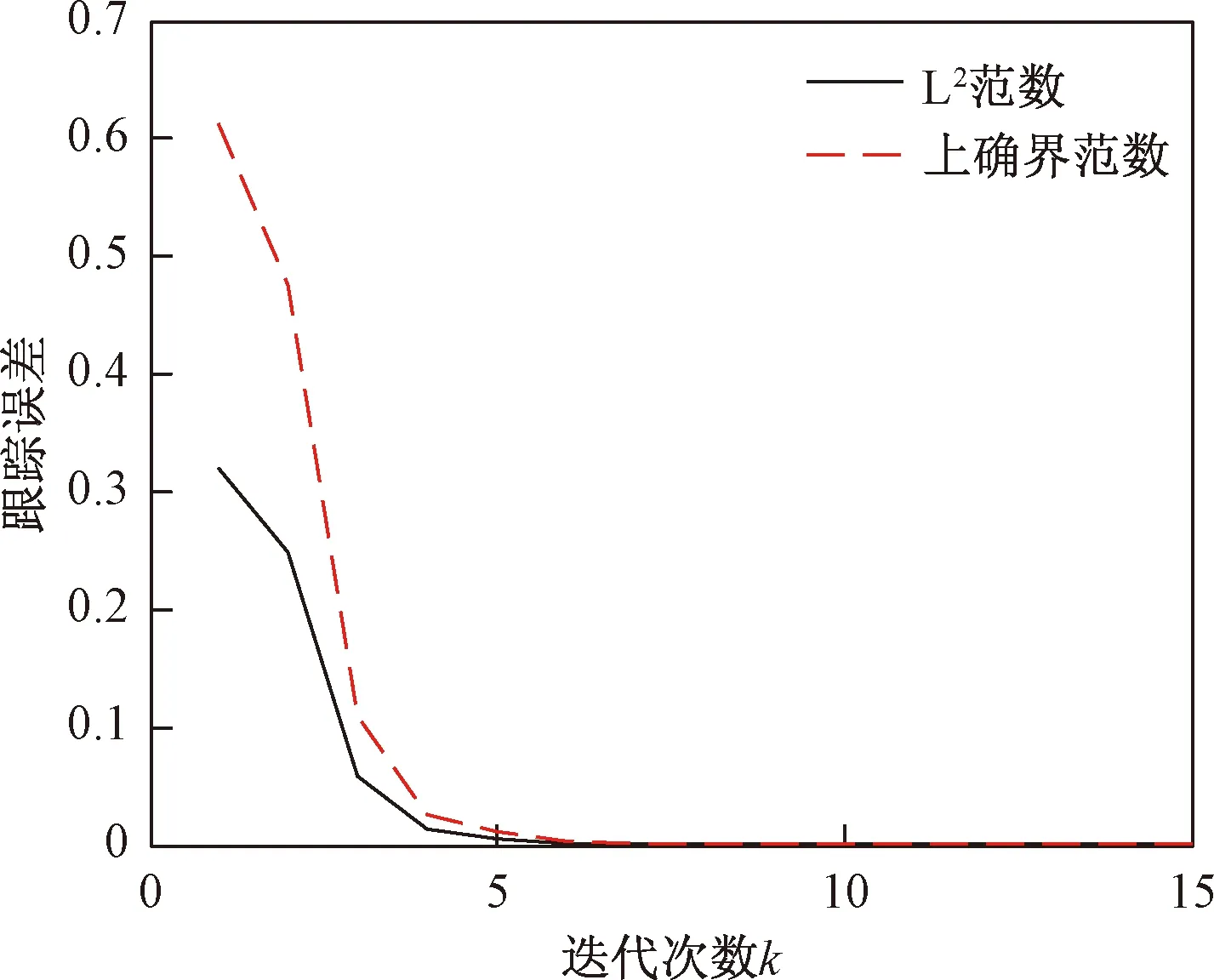
式(1)中,x(t)∈Rn、u(t)∈Rm、y(t)∈Rq分别为系统状态量、控制输入量和系统输出量;A∈Rn×n、B∈Rn×m、C∈Rq×n为定常矩阵;E∈Rn×n是一奇异矩阵,即rank(E)=r (2) 其中,A11∈Rr×r,A12∈Rr×(n-r),A21∈R(n-r)×r,A22∈R(n-r)×(n-r),B1∈Rr×m,B2∈R(n-r)×m。 则式(2)变为 (3) 为了证明方便,下面给出算法的合理假设。 假设1对于在[0,T]上可微的期望输出yd(t),有唯一的理想控制输入ud(t),使得系统的状态和输出为xd(t)和yd(t)。 假设2A22可逆。 设初次的控制输入u1(t)(t∈[0,T])为一任意值。二阶P型迭代学习控制算法LP(γ1,γ2)的表达式如下: (4) 式(4)中,Γ1和Γ2表示比例学习增益矩阵,加权系数γ1和γ2满足:0≤γ1≤1、0≤γ2≤1且γ1+γ2=1;ek(t)=yd(t)-yk(t),表示第k次迭代时系统的跟踪误差。 当γ1→1-时,LP(γ1,γ2)趋于一阶P型控制算法LP(1),其表达式如下: uk+1(t)=uk(t)+Γ1ek(t),k=1,2,3,… (5) 证明:由式(3)和假设2,可得: (6) (7) 所以: (8) 记: Δxk(t)=xd(t)-xk(t) (9) Δuk(t)=ud(t)-uk(t) (10) 由于: (11) 根据假设3,可得: (12) (13) 因此: ek(t)=yd(t)-yk(t)=CΔxk(t)= (14) 由式(4),可得: (15) 式(15)两端取Lp范数,并应用卷积的推广Young不等式,得: (16) 由定理条件,可知: γ1ρ1+γ2ρ2<1 (17) 根据引理2,可得: (18) 由式(14),可得: (19) 式(19)两端取Lp范数,并应用卷积的推广Young不等式,得: (20) 当γ1→1-时,二阶P型控制算法LP(γ1,γ2)趋于一阶算法LP(1),当LP(1)施加于线性广义系统[式(1)]时,有如下结论。 根据Qp因子的大小,可判断控制算法收敛速度[16]。利用Qp因子方法,比较了两种P型控制算法[式(4)、式(5)]的收敛速度,获得以下结论: 注:从定理证明过程可知,在Lp范数意义下,跟踪误差的度量和控制算法的收敛性分析不受λ取值的影响。 考虑如下线性广义系统: (21) 在二阶P型控制算法(4)中,取Γ1=0.25,Γ2=0.6,γ1=0.5,γ2=0.5,计算可得ρ1=0.589 8<1,ρ2=0.175 6<1,满足定理的条件。在控制算法[式(4)]作用于下,广义系统[式(21)]的第4次、第6次的实际输出与期望输出yd(t)如图1所示。发现,当迭代次数逐渐增大时,可以实现系统实际输出对期望输出的完全跟踪。 当二阶P型控制算法[式(4)]作用于广义系统[式(21)]时,图2给出了在上确界范数和L2范数的意义下,系统跟踪误差曲线的变化趋势。从图2中可以发现,当迭代次数逐渐增加时,在两种范数意义下,跟踪误差都单调趋于0。 图1 系统输出的跟踪效果Fig.1 Tracking effect of system output 图2 两种范数意义下的跟踪误差Fig.2 Tracking errors in the sense of two norms 图3 跟踪误差对比Fig.3 Comparison of tracking errors 在对线性广义系统进行非奇异变换的基础上,在Lp范数意义下,本文利用卷积的推广Young不等式,研究了一、二阶P型迭代学习控制算法的收敛性,获得其收敛的条件,并利用Qp因子方法比较了两种控制算法的收敛速度。结果表明,控制算法的收敛条件、收敛速度与学习增益矩阵以及系统本身属性有关;如果选取合适的学习增益矩阵,则二阶P型控制算法的收敛速度要比一阶的快。这种研究方法,可用于继续分析非线性广义系统的收敛性态。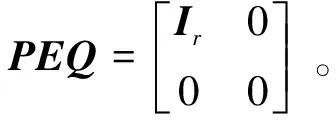
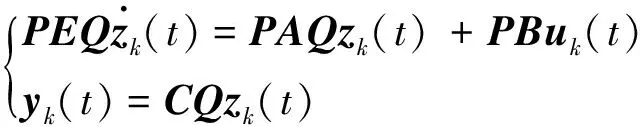
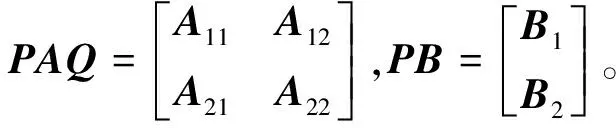

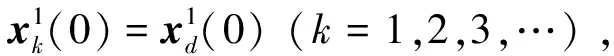
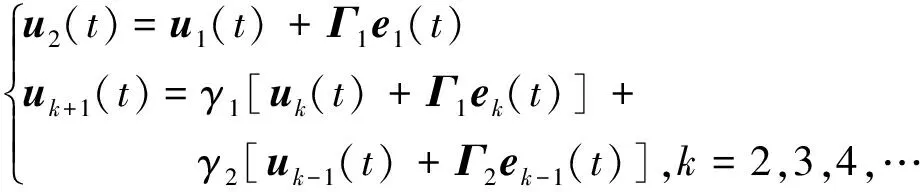
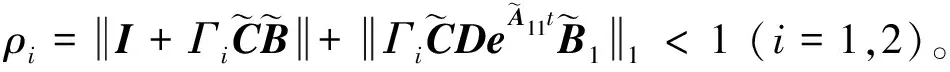
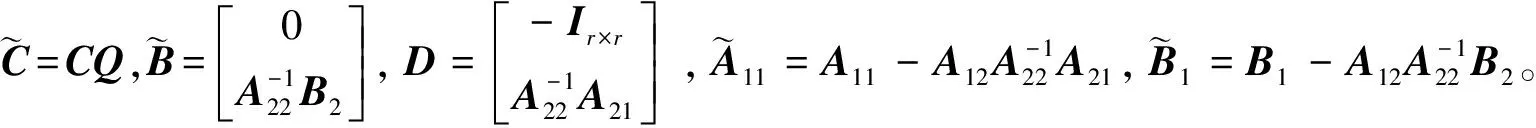
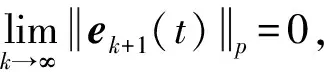


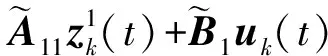
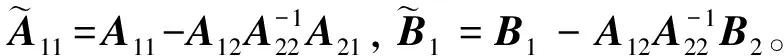
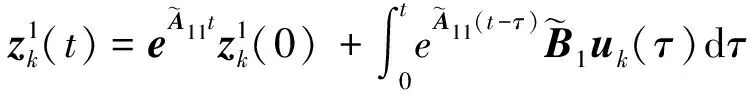
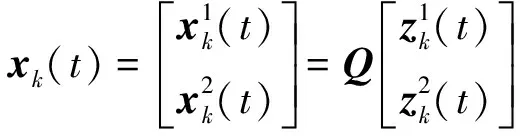

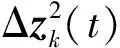
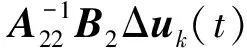


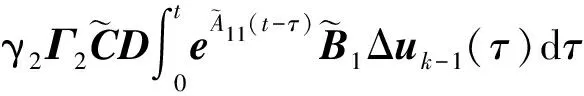
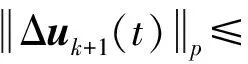
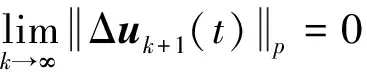
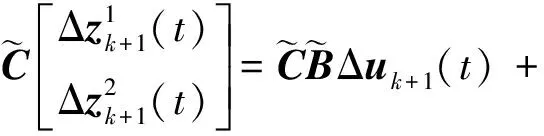


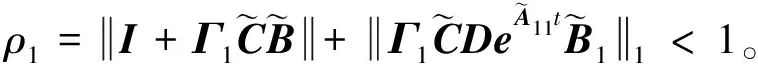
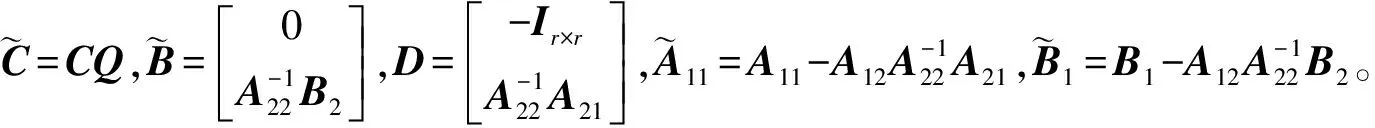
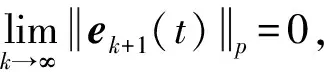
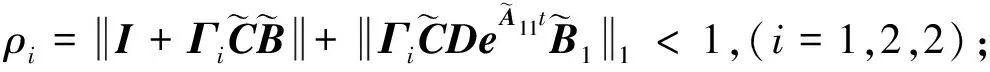
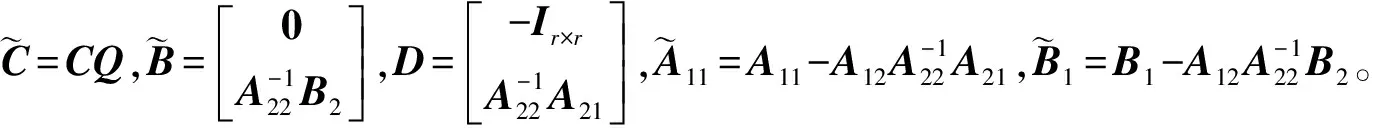
3 数值仿真
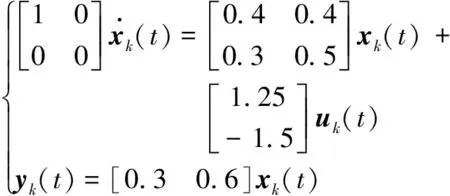
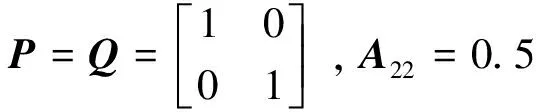


4 结论
