用于线性规划的诊断与决策可视化

韦东鑫

（四川大学计算机学院，成都610065）

0 引言

线性规划是在各种约束条件下构建线性规划模型并从中挑选出最合适的计算方法，进而求解出最佳结果。线性规划目前被广泛应用于现有数学计算方法中并能够解决工作生活中的各种实际问题，但要想将现实问题抽象为线性规划模型存在着诸多困难，例如，分析人员需要足够的先验知识才能很好地在各种约束条件下完成对现实问题的抽象，线性规模模型中的参数难以预先确定。此外，大规模复杂的线性规划求解结果难以让用户进行分析且难以理解。

人眼的感知能力是目前已知的最强生物感知系统，人眼对图片的识别能力要远远超出对数字与文字的识别。可视化利用人眼的强感知能力将数据转换为可交互的可视化图像，能够增强数据识别效率，传递有效信息。将可视化运用于线性规划，可在数据层面为复杂的线性规划问题提供解释与诊断，通过可视化技术，基于统计图表的隐喻方法设计视图并增加多种交互方法，能够帮助理解复杂的决策变量与约束关系。

本文结合线性规划与可视化两种方法，围绕如何在控制饲养成本的前提下保证宠物猫的营养摄入问题进行研究，设计并实现了多种可视化视图，并利用视图对线性规划求解结果进行展示，帮助用户快速理解线性规划的优化结果，对决策变量的数据流向进行追踪从而对约束的逻辑含义进行解释，且可以辅助观察者对约束进行调整。此外，本文使用的可视化视图能够帮助观察者理解决策变量之间的数值关系和逻辑关系，采用探索式的方法进一步挖掘数据中的信息。

1 数据描述与线性规划求解

1.1 数据获取与处理

本文采集的所有数据可分为三类：①宠物猫的各类营养物质需求量；宠物猫所需的营养物质总体可概括为7 种：蛋白质、碳水化合物、钙元素、脂肪、磷元素、维生素E 和锌元素。②各类食材的出售价格；本文从在线生鲜平台上采集了各类食材的出售价格，由于食材的种类繁多且价格不一，因此统一以销量最高的食材所对应的价格为准。③各类食材所含的营养成分信息；本文从美国农业部公开的USDA 数据库中获取到了常见的各类食材中所含的上述7 种营养成分信息。在采集到足量的数据后，本文对数据集进行了脏值与错值去除、数据结构化以及存储等处理工作。

1.2 线性规划求解

本文所研究的问题为如何在控制饲养成本的前提下保证宠物猫的营养提供，将这一实际问题抽象为线性规划模型可得到如式（1）所示的数学模型，其中i，j分别对应不同食材的编号与不同营养物质的编号，xi，ci分别表示每种食材的数量以及宠物猫对该种食材的最低需求量，ni，N 分别表示第i 种食材所含的营养成分与宠物猫所需的营养最低值，pricei表示单种食材的价格。

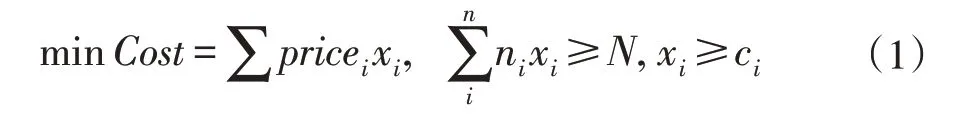
由此可知该线性规划模型实际上可视为最小成本函数，对上述实际问题的求解也就是对该最小成本函数求最优解。本文使用Python 语言下开放的IBM Cplex API 对线性规划模型进行求解，在后续中将重点描述如何在不断调整参数并求解时，使用可视化方法来对线性规划求解结果进行展示，从而辅助得到最优解。

2 可视化模型构建与视图设计

2.1 可视化模型描述

在现实生产生活中，线性规划中的约束提取往往依赖于分析人员对问题的理解，也即约束式通常具有实际的现实含义。在设计线性规划优化方案时，由于实际问题或约束引入了诸多不确定性，因此难以对约束逻辑和参数进行控制，要在这样的条件下引入数学模型来解决管理优化问题变得异常困难。通过可视化的方法可以逐步探索、验证与分析数据信息，且对模型理解具有重要意义。本文结合数据与实际问题，提出了如图1 所示的可视化模型，并依据该模型使用多种方法对1.2 小节中的最小成本函数进行分析，解释模型中各类约束与决策变量间的关联关系并最终实现对函数的最优求解。

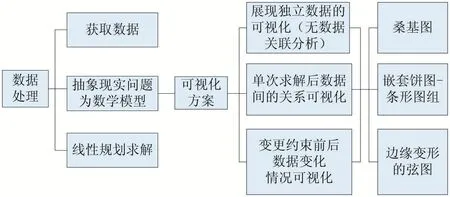
图1 可视化模型

2.2 可视化任务抽象

为了更好地理解线性规划问题中的约束与决策变量，本文结合可视化模型与宠物猫营养供给实际问题，对涉及到的可视化任务进行分类，提出了如表1 所示的可视化任务与对应的现实问题。针对不同类别的可视化任务设计并实现了多种可视化方法，使用可视化方法对求解后的线性规划模型各类参数、约束条件进行展示，发现决策变量间的取值与关联关系并呈现该决策变量对约束的贡献，尝试找出可相互替代的决策变量。

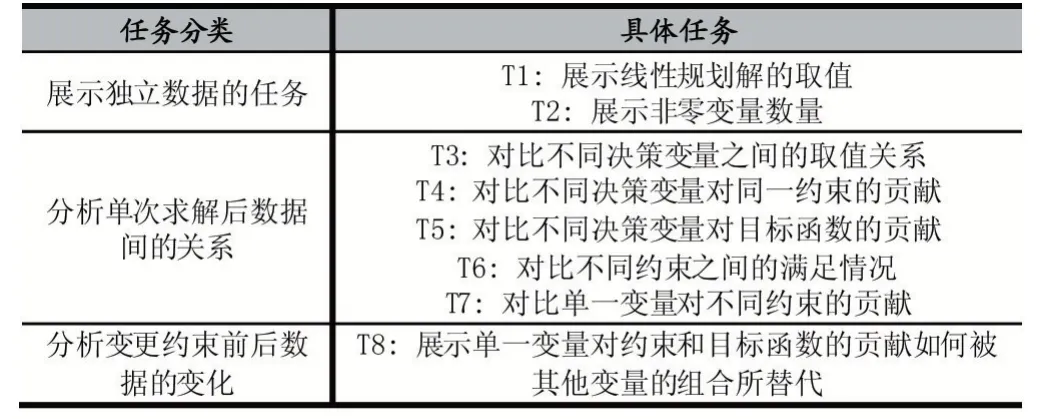
表1 可视化任务

2.3 可视化方法

本文设计了如图2 所示的桑基视图，在视图中不同的色块表示不同的决策变量，以颜色区分决策变量的类别，色块的宽度表示单个决策变量对目标函数的贡献，色块间的连接表示决策变量之间的层次关系。该视图中的数据分组由用户自行定义，可以按照食材所属动物物种或食材所属部位进行分类，允许用户在不同的角度对线性规划模型求解结果进行打包分析，且利用分组与层次关系减少认知负担，发现不同分组间的比较关系。从视图中可发现经过线性规划求解后，第一次求解结果中只有鸡心、蛋黄、肝脏、鲭鱼和鹌鹑五种食材，其中鸡肉类即红色色块最多。

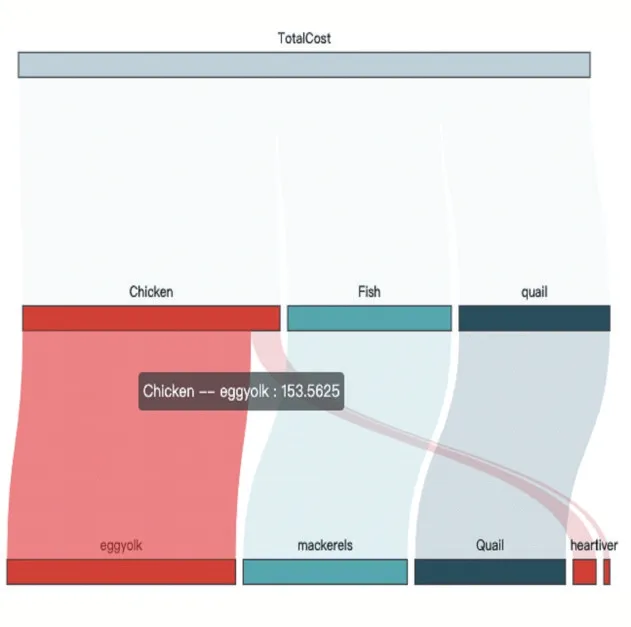
图2 用于线性规划分析的桑基图

本文对嵌套饼图与分组柱图进行组合，得到如图3所示的可视化视图。该视图中以面积表示单个决策变量对约束的贡献，也即单个决策变量对约束的贡献占比，此外，嵌套饼图中的嵌套关系用于表示层次关系，不同层级的约束相互嵌套。因为嵌套饼图的大小是固定的所以当模型求解结果超出约束条件越多则嵌套的圆越大。分组柱图可以直观地展示不同决策变量在满足同一个约束上的贡献差别，因两个视图采用了相同的颜色映射方式，所以用户只需对颜色进行观察追踪便能够在不同组之间进行同一变量在满足不同约束时贡献高低的比较。

从绘制的桑基图和嵌套饼图-条形图组中可以发现：鸡对目标成本贡献值最高。进一步从嵌套饼图-条形图组分析，很明显看出猫摄入的脂肪含量远远超过脂肪的最低摄入量，这样的营养配比明显不太合理，应再进一步关注其他营养成分情况。

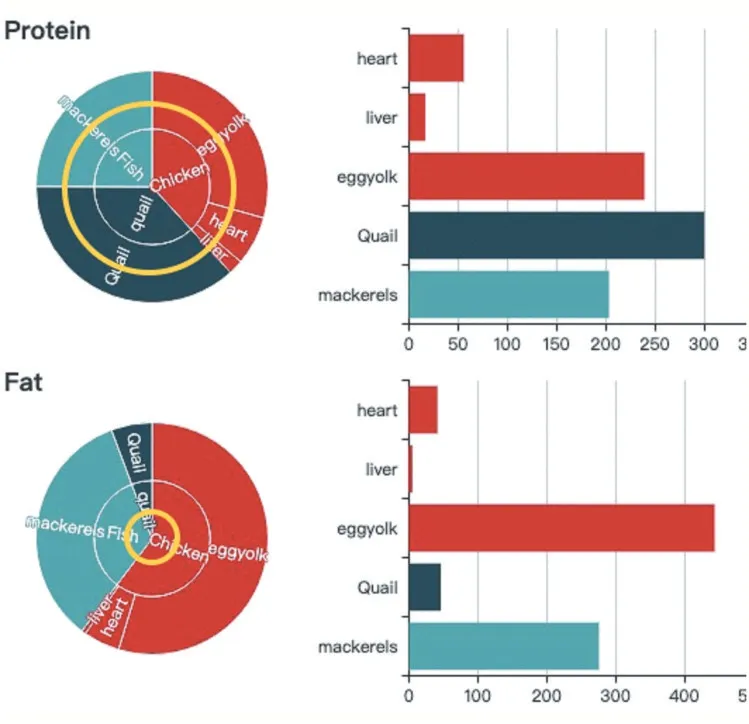
图3 嵌套饼图-分组柱图

从图4 中可以明显发现：钙元素、锌元素、维生素E 和碳水化合物中的营养大部分来自蛋黄。这里的蛋黄（每个30 克）每周提供1.5 千克，如果要达到首次计算出的配方，那么需要每周为猫提供高达50 个的蛋黄数量，明显是不太切合实际情况的。所以就需要考虑决策变量的变更，因为钙和维生素E 的主要来源都是蛋黄，所以加入钙粉和维生素E 进入决策变量，再次计算并可视化。

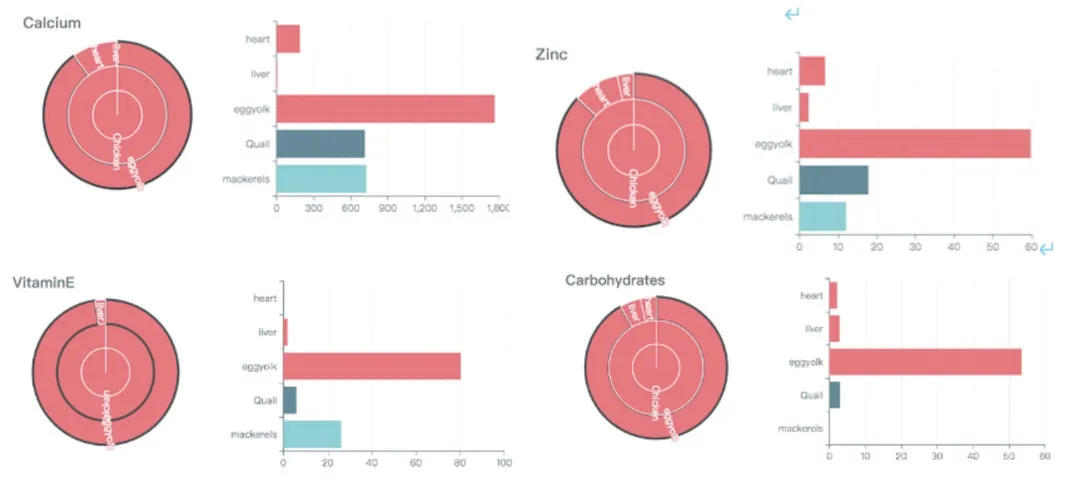
图4 多种营养成分分析

本文在和弦图的基础上进行改进，得到了边缘变形的和弦图。该视图使用径向圆弧的弧长表示单个决策变量的大小，圆弧的宽度表示对应决策变量被替换而引入的额外支出。圆弧之间的弦表示可被替代的关系，同样地，以颜色区分不同的类别。此视图以红色的圆弧为主，可以看出红色圆弧所代表的决策变量可以被绿色、藏蓝、粉色弦所连接的圆弧对应的决策变量替代。如图4 所示，蛋黄可以被鸡肝、鲭鱼、鸡心和鹌鹑替代，但是蛋黄自身一部分无法被替代，也就是说在此种组合策略下宠物猫必须摄入一定量的蛋黄。图中绿色弦与红色圆弧连接处出现了明显的边缘凸起，表明若使用鲭鱼替代蛋黄会增加额外的成本，边缘凸起的高度越大表示决策变量替换后线性规划模型的值越大。

3 结语

本文针对线性规划诊断和决策问题进行了可视化方法的研究，具体工作主要分为几个方面：首先根据实际生活中存在的问题提出了可视化分析任务，建立了可视分析模型。然后，针对可视化任务提出了三种可视化方法，分别为桑基图可视化方法、嵌套饼图-条形图组可视化方法、边缘变形的弦图可视化方法。最后以宠物猫营养供给为例进行分析，分析结果验证了可视化方法的有效性。