三角直觉模糊数理论在供应商选择中的应用

赵未莲

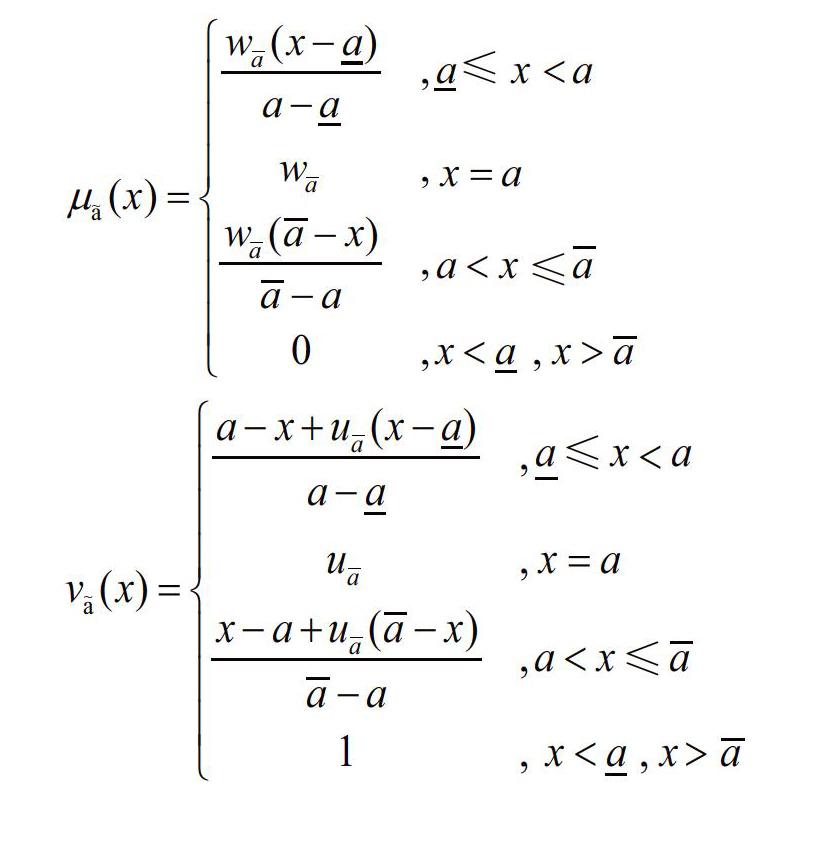
摘   要：随着社会的发展，物质极大地丰富，人们的需求也多样化，为人们提供服务的供应商越来越多，如何选择满意的供应商也是生活中非常重要的事情，基于社会现实文章首先阐述了三角直觉模糊数的理论知识，继而将一种基于两个三角直觉模糊数之间距离的决策方法应用在供应商的选择中。

关键词：直觉模糊数;三角直觉模糊数;距离;决策

19世纪末，Cantor首创集合论[1]，并快速渗透到各个数学分支，成为数学的基础。1965年美国控制论专家L.A.Zadeh发表了开创性论文“模糊集合”（Fuzzy Sets，Information and Control），对Cantor的集合论进行了有益的推广，从而建立了模糊集合论，且在很多领域取得了卓有成效的应用。简言之，模糊数就是表示一个不确定的量。1986年Atanassov提出直觉模糊集的概念，直觉模糊集是模糊集的扩展，比模糊集在处理模糊性和不确定性方面更具灵活性和实用性[1]。直觉模糊数的特点是同时考虑隶属函数、非隶属函数和犹豫度3方面的信息，因此直觉模糊数可以更好地表示一个不确定的量，随着直觉模糊理论的发展，又有学者定义了三角直觉模糊数及其代数运算和排序方法，并应用在多属性决策中。本文从实际出发，将三角直学模糊数的理论应用在供应商的选择中，使计算更方便，复杂度更低，易于实现，更直观地选出供应商。

1    三角直觉模糊数

定义1 设～a是实数集上的一个直觉模糊集[2]，其隶属函数与非隶属函数分别为：

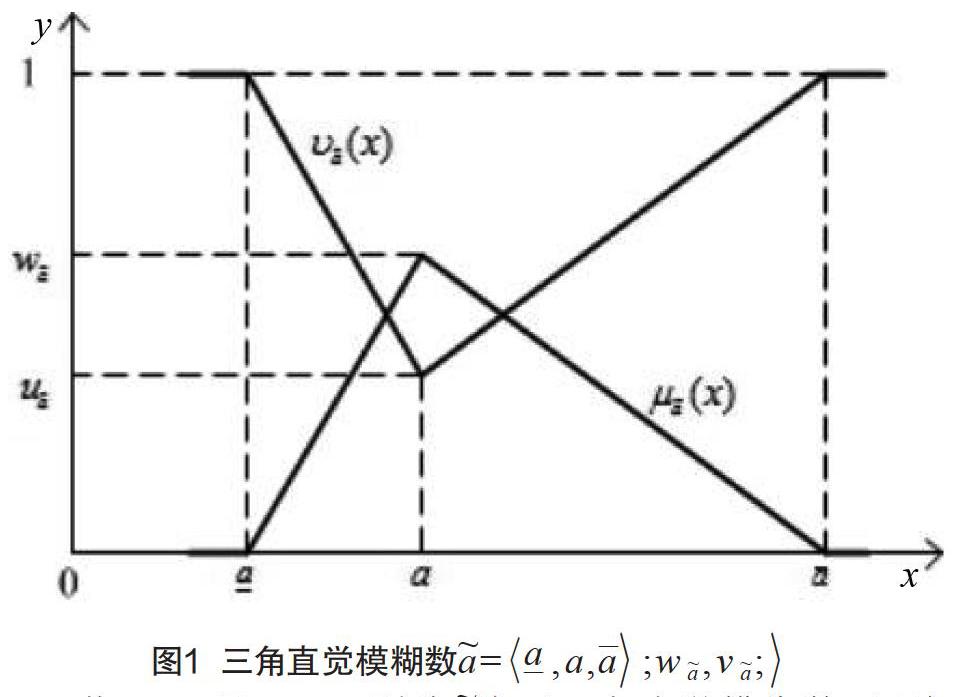
其中，0≤w_a≤1，0≤u_a≤10≤w_a+u_a≤1;称～a=〈_a，a，_a〉;w～a，v～a;〉为三角直觉模糊数[2]（triangular intuitionistic fuzzy number，TIFN），w_a为最大隶属度，u_a为最小非隶属度，π _a=1-w_a-u_a为～a的犹豫度，其值越小，表示模糊数越确定，曲线如图1所示。

若_a≥0且_a>0，则称～a为正三角直觉模糊数，记为～a>0[2]。类似地，若_a≤0且_a>0，则～a为负三角直觉模糊数，记为～a<0。三角直觉模糊数～a表示实数a的近似值。不确定量～a用介于_a和 _a之間的任意实数表示，且每个实数具有不同的隶属函数和非隶属函数。不确定量～a最可能的值a，其隶属度和非隶属度分别为w_a和u_a;不确定量～a最不可能的值是_a和_a，其隶属度和非隶属度分别为0和1，在开区间（_a，_a）内任意数x的隶属度和非隶属度分别为w～a和v～a。

显然，当w_a=1和u_a=0时，即直觉指数（犹豫度）为0，非隶属函数形成的反对程度最强。当犹豫度（直觉指数）大于0时，亦即非隶属函数形成的反对程度减弱时，所得结果的可信度将会更高、更有效。

定义2 三角直觉模糊数～a=〈_a，a，_a〉;w～a，v～a;〉，0≤_a≤a≤_a≤1[2]，称～a为规范化的三角直觉模糊数，规范化的三角直觉的正理想点和负理想点分别为：

～a+=〈（_a+，a+，_a+〉;w+～a，v+～a;〉=〈（1，1，1，）;1，0〉，～a_=〈（_a_，a_，_a_〉;w_～a，v_～a;〉=〈（0，0，0，）;0，1〉。运算：λ～a=〈（λ_a，λa，λ_a〉;w～a，v～a;〉

2    改进的直觉模糊集（IFS）之间的距离

距离能方便地表达两个对象之间的区别，直觉模糊集之间的密切程度可用距离来表示[3]。目前定义两个对象的距离有多种方法，如汉明距离、欧氏距离等。

贺正洪等根据IFS的几何解释，同时考虑隶属度、非隶属度和犹豫度三部分，并注意区分犹豫度与隶属度、非隶属度作用的不同，提出一种新的距离度量公式，下面主要列出欧氏距离公式：

（1）

上式中的取值可根据实际需要调整，当ρ=0时，就是不考虑犹豫度对距离的影响;当ρ=1时只考虑了犹豫度的作用，但没有考虑犹豫度与隶属度及非隶属度在距离计算中所起作用的不同。一般弃权部分既有支持倾向者又包含有反对倾向者，在没有其他先验信息的情况下，一般认为支持与反对者各占一半是比较合理的，所以取比较合适，若没有特别说明，默认。

3    实例分析

下面提出一种基于三角直觉模糊数的距离多属性决策方法，具体步骤如下。

第一步，采用专家问卷调查，统计方法与语言变量法，抽取并构造适当的三角模糊决策矩阵A=（～aij）n×m，其中：

第二步，对三角直觉模糊决策矩阵归一化，转化为

对成本型属性用公式：

（2）

对效益型属性用公式：

（3）

其中

第三步，用下述公式计算综合值：

Xi的隶属度

Xi的非隶属度  （4）

第四步，用之间的距离对方案进行优劣排序，与～a+的距离越小的xi越优，因为此距离越小说明离正理想点越近，即支持率越高;与～a_的距离越大的xi越优，因为此距离越大说明离负理想点越远，即反对率越低也就是支持率越高。下面举一个实例进行分析：

某单位要招供应商，经过初步筛选后，需要对3家供应商即x1，x2，x3进行考核并最终确定供应商。该单位拟定5个考核指标：信用度（g1）、产品价格（g2）、交货期（g3）、产品品质（g4）、服务水平（g5）。假设初始权重为：w=（0.14，0.30，0.12，0.30，0.14）T，各供应商各属性的评估信息经统计处理后得到三角直觉模糊数。三角直觉模糊数如表1所示。

决策方法：（1）g2，g3是成本型属性，选择公式（2）进行归一化;g1，g4，g5为效益型属性，选择公式（3）进行归一化，结果如表2所示。（2）用公式（4）计算各供应商的综合评价值。

x1=〈（0.413，0.586，0.730）;0.6，0.4〉，

x2=〈（0.429，0.55，0.660）;0.4，0.5〉，

x3=〈（0.359，0.475，0.674）;0.5，0.2〉，

（3）用xi與～a+=〈（1，1，1）;1，0〉和～a_=〈（0，0，0）;0，1〉的距离对方案进行优劣排序。

eM（x1，～a+）=0.674，eM（x2，～a+）=0.793，eM（x3，～a+）=0.751，

eM（x1，～a_）=0.94，eM（x2，～a_）=0.877，eM（x3，～a_）=0.934，

按xi与～a+的距离排序的优先顺序为：x1>x3>x2;按xi与～a_的距离排序的优先顺序为：x1>x3>x2。

两者的优先顺序相吻合，说明此法可行。

4    结语

本文讲述了三角直觉模糊数及欧氏距离公式，用一般三角模糊数与理想正、负三角模糊数之间的距离进行优先排序，这种方法同时考虑了隶属度、非隶属度及犹豫度的影响，方法简单易懂、计算量不大、可操作性强。

[参考文献]

[1]梁保松，曹殿立.模糊数学及其应用[M].北京：科学出版社，2007.

[2]余高锋，李登峰.三角直觉模糊决策的权重函数方法[J].计算机科学与探索，2014（10）：1263-1270.

[3]雷英杰，赵杰，贺正洪，等.直觉模糊集理论及应用[M].北京：科学出版社，2014.

[4]李柏年.模糊数学及其应用[M].合肥：合肥工业大学出版社，2007.

Application of triangular intuitionistic fuzzy number in supplier selection

Zhao Weilian

（Modern Economics & Management College of JXUFE， Nanchang 330013， China）

Abstract：With the development of society， the material is greatly enriched， and peoples needs are diversified. More and more suppliers provide services for us. How to choose satisfactory suppliers is also a very important thing in our life. Based on social reality， this paper first expounds the theoretical knowledge of triangular intuitionistic fuzzy numbers， and then applies a decision-making method based on the distance between two triangular intuitionistic fuzzy numbers in supplier selection.

Key words：intuitionistic fuzzy numbers; triangle intuitionistic fuzzy number; distance; decision