滑移隔震结构与相邻建筑物的碰撞分析
2020-04-21方雷庆刘廷滨
方雷庆 刘廷滨
(1.中信建筑设计研究总院有限公司,武汉430014;2.兰州交通大学土木工程学院,兰州730070)
0 引 言
基础滑移隔震技术是在房屋上部结构与基础之间设置由低摩阻材料构成的可滑移的隔震层,隔震层的滑移错动隔离了传向上部结构的地震力,从而保证了结构免于地震破坏。当结构滑移值较大,与相邻建筑物的距离较小时,会与相邻建筑物发生碰撞。结构碰撞会导致建筑结构性破坏或非结构性破坏,给人类的生命财产造成巨大的损失。
Malhotra[1]和 Tsai[2]最早研究了隔震结构的碰撞问题,分析了各种参数对隔震结构碰撞反应的影响;Nagarajaiah 等[3]介绍了在 Northridge 地震中基础隔震结构发生碰撞的情况;Matsagar 和Jangid[4]研究了对不同类型的隔震结构在地震作用下与相邻附属结构的碰撞反应;谷伟等[5]建立了滑移隔震啮合状态判别准则,研究了带限位器滑移隔震结构考虑竖向地震作用的影响;樊剑等[6]对近断层地震下摩擦型隔震结构与限位装置碰撞反应及防护进行了研究。本文以纯摩擦滑移隔震结构(P-F)和恢复力滑移隔震结构(R-FBI)为研究对象,采用Hertz-damp碰撞模型,研究地震作用下滑移隔震结构与相邻建筑物之间的碰撞反应,并研究了防震缝宽度、摩擦系数以及碰撞刚度等因素对隔震结构碰撞反应的影响。
1 分析模型及碰撞运动方程的建立
P-F 和R-FBI 隔震结构与相邻建筑物的计算简图如图 1 所示[6],单体 A 为隔震结构,单体 B 为非隔震结构,单体A 和单体B 的层数分别为n1和n2,首先对单体A建立运动方程。

图1 结构碰撞计算模型Fig.1 Analysis model of structural pounding
当结构体系所受惯性力小于最大静摩擦力时,隔震层与基础之间无相对运动,体系处于啮合状态,相当于传统的基础固定结构,为n1个自由度。水平运动方程为

当结构体系所受惯性力大于最大静摩擦力时,隔震层与基础之间发生相对滑动,隔震层受到的摩擦力达到最大值,并随滑动方向改变而改变,体系变为n1+1个自由度,水平运动方程为
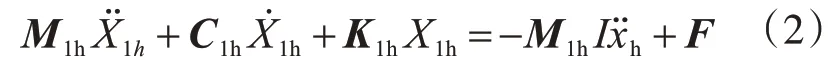
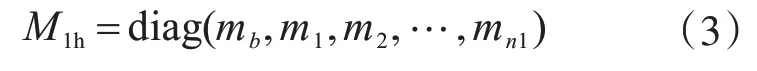
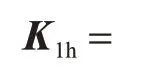

式中,ωh'1,ξ为结构水平振动的基频和阻尼比,ξ取0.05。
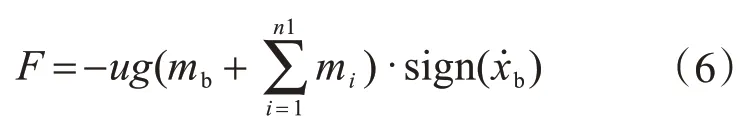
式中:F为摩擦力列向量,按下式取值;sign为表示方向的符号函数。
当体系处于啮合状态时发生碰撞,则结构体系的运动方程组为
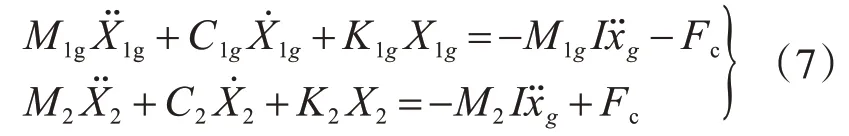
当体系处于滑移状态时发生碰撞,则结构体系的运动方程组为

将方程组(7)写成等效形式:

其中,

将方程组(8)写成等效形式:
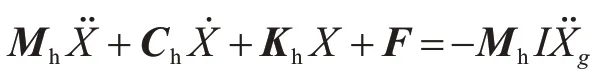
其中,
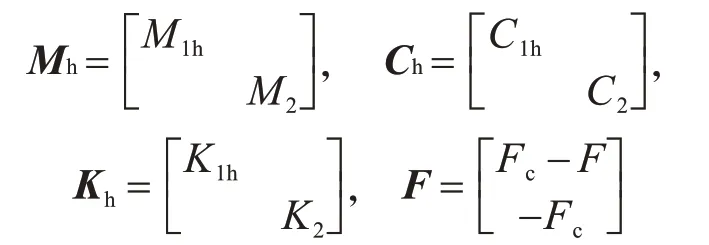
隔震体系在地震作用下,总是处于滑动状态与啮合状态不断交替之中,其状态转换的判别条件是:当满足式(9)时,结构处于滑动状态;当满足式(10)时,结构处于啮合状态[5]。
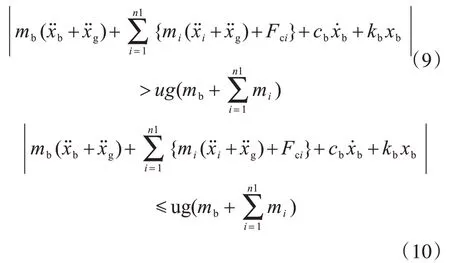
本文碰撞模型选取 Hertz-damp 模型[7],此模型认为碰撞过程中两物体质心在相互接近和离开的阶段都有能量损失,碰撞力表达式为
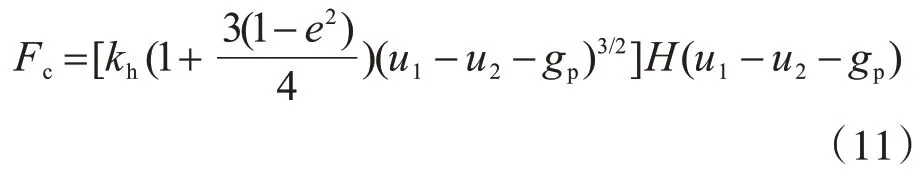
式中:u1,u2为两个物体的位移;gp为两个物体的初始距离,kh为碰撞刚度;H(·)为 heaviside 单位阶跃函数;e为恢复系数,对于完全弹性碰撞,e=1,完全塑性碰撞,e=0,对于混凝土材料,e=0.65[8]。
2 算例分析
本文单体A 取五层的P-F 和F-RBI 隔震结构为分析实例,结构的质量和刚度沿楼层均匀分布,基底质量和各单层质量为100 t,楼层层间弹性刚度为5×108N/m,基底摩擦系数u=0.05,结构阻尼比ξ=0.05;F-RBI 隔震结构隔震层水平刚度为1×107N/m,阻尼比为0.05。相邻建筑单体B 为五层框架结构,各单层质量为100 t,楼层层间弹性刚度为1×109N/m,两建筑防震缝宽度为120 mm。输入地震加速度记录为El Centro 波(南北方向),其加速度峰值调到400 gal(相当于8度)。据文献[7],碰撞刚度取8.686 8×105kN/m2/3。采用Matlab编程,得出两种隔震结构碰撞和不碰撞两种情况下的地震响应时程。
2.1 反应时程分析
从图2可看出,P-F滑移隔震结构与相邻建筑物在3 s 附近发生碰撞,碰撞产生加速度脉冲,单体A 峰值加速度达到18.49 m/s2,而不考虑碰撞时峰值为8.92 m/s2,考虑碰撞是不考虑碰撞的的2.07 倍。单体B 峰值加速度达到17.21 m/s2,而不考虑碰撞时峰值为12.57 m/s2,考虑碰撞是不考虑碰撞的的1.34倍。地震作用下,单体A发生滑移,由于P-F 滑移隔震结构没有恢复刚度,滑移位移较大,考虑碰撞时和不考虑碰撞时,单体A顶层最大位移分别为0.46 m 和0.33 m,而隔震层最大位移分别为0.45 m 和0.30 m,顶层最大位移基本上由隔震层的位移组成。从而表明:当碰撞发生时,结构加速度和位移均有较大增加,由于P-F 滑移隔震结构自身位移较大,当存在相邻结构时,很难不发生碰撞,所以在实际工程中,对P-F 滑移隔震结构应增设限位装置或者在结构周边一定距离内不允许存在其他构筑物。采取最大层间位移及底部最大剪力时程来分析结构的抗震性能,考虑碰撞时和不考虑碰撞时,单体A 最大层间位移分别为39.9 mm 和31.2 mm,底部最大剪力均为2.02×104kN。由于碰撞的发生,最大层间位移增大了27.8%,假设一框架结构的层间位移角为1/550,当增大27.8%时层间位移角可达到1/430,从而可知,碰撞不仅对碰撞部位产生破坏,也对结构整体造成非常不利的影响。由于P-F 滑移层的存在,碰撞力被滑移层吸收,底部最大剪力没有明显的变化。
从图3可看出,R-FBI滑移隔震结构与相邻建筑物在3 s和12.5 s附近发生碰撞,其中3 s发生的碰撞加速度脉冲较大,单体A 峰值加速度达到18.59 m/s2,而不考虑碰撞时峰值为8.44 m/s2,考虑碰撞是不考虑碰撞的的2.2 倍。单体B 峰值加速度达到17.27 m/s2,而不考虑碰撞时峰值为12.57 m/s2,考虑碰撞是不考虑碰撞的的1.37 倍。由于R-FBI 滑移隔震结构具有恢复刚度,滑移位移比P-F 滑移隔震结构大大降低,考虑碰撞时与不考虑碰撞时,单体A 顶层最大位移分别为0.18 m 和0.22 m,而隔震层最大位移分别为0.16 m 和0.20 m。R-FBI 滑移隔震结构考虑碰撞时和不考虑碰撞时,单体A 最大层间位移分别为37.7 mm 和31.2 mm,底部最大剪力分别为 2.01×104kN 和1.96×104kN。由于碰撞的影响,最大层间位移增大了20.8%,相对于P-F 滑移隔震结构,碰撞对层间位移的影响降低,但仍有较大的增加。由于恢复刚度的存在,碰撞力没有完全被滑移层吸收,底部最大剪力有较小的增加。
2.2 防震缝宽度的影响

图2 地震响应时程曲线(P-F隔震结构)Fig.2 Typical time histories of structural earthquake response(P-F isolated structure)
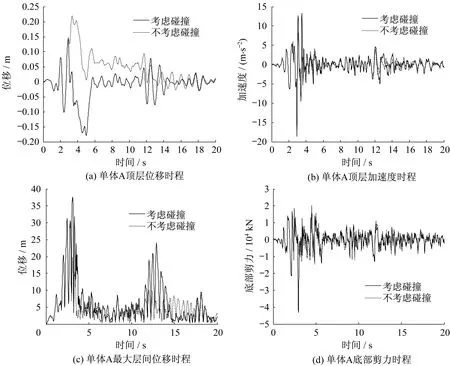
图3 地震响应时程曲线(R-FBI隔震结构)Fig.3 Typical time histories of structural earthquake response(R-FBI isolated structure)
《建筑抗震设计规范》(GB 50011—2010)规定了防震缝宽度的最小值,但在强烈地震下相邻结构仍可能局部碰撞而损坏,而对于滑移隔震结构,地震作用下其位移响应更大,发生碰撞的可能性大大增加。由于P-F 滑移隔震结构没有恢复刚度,其地震反应下的位移没有规律可寻,防震缝宽度的影响研究意义不大,本文单独对R-FBI 滑移隔震结构进行分析。假设其他条件不变,随防震缝宽度的变化,得到考虑碰撞和不考虑碰撞两种情况下的结构顶层最大位移、最大加速度的变化曲线,如图4所示。从图4可看出,只要发生碰撞,单体A 和单体B 的结构加速度响应都会增加。当防震缝宽度较小时,结构相互间发生高频碰撞,随着防震缝宽度的增大,单体A 结构顶层最大位移会在一定区间内变化,但变化区间的最大值会逐渐变小,随后逐渐趋于平稳,相邻建筑的限位作用得到明显体现,此时考虑碰撞时的顶层最大位移已小于不考虑碰撞时,随着防震缝宽度的继续加大,碰撞力越来越小,最大位移会渐渐回归至与不考虑碰撞时相同。单体B结构顶层最大位移在防震缝宽度较小时会随着防震缝宽度有所变化,但由于单体B 刚度较大,当防震缝宽度达到70 mm左右时,碰撞力已不能使单体B 位移发生变化。单体A 和单体B 的顶层最大加速度变化趋势基本一致,随着防震缝宽度的增大,最大加速度会逐渐变大,在防震缝宽度达到70 mm左右时,最大加速度达到峰值,随后不断变小,并逐渐回归到与不考虑碰撞时相同。由于单体B 刚度较大,其加速度先于单体A回归。

图4 顶层位移,加速度随防震缝宽度变化曲线(R-FBI隔震结构)Fig.4 Displancement,acceleration on top floor varying with width of seismic joint(R-FBI isolated structure)
2.3 摩擦系数的影响
聚四氟乙烯作为滑移材料得到广泛的应用,但其材料的冷流性会导致耐久性降低,限制了材料的使用,二硫化钼、二硫化钨等其他固体润滑材料作为新的滑移隔震层材料得到越来越多的重视。隔震层材料不同,摩擦系数也随之不一样,而与相邻结构的碰撞会导致结构响应更加复杂,因此有必要弄清摩擦系数对隔震结构的影响。本文以R-FBI滑移隔震结构为例,假设其他条件不变,随摩擦系数的变化,得到结构顶层最大位移、最大加速度的变化曲线,如图5 所示。由图5 可以看出,当摩擦系数为0 时,滑移隔震结构变成了普通的基础隔震结构。由图可知,随着摩擦系数的增加,加速度响应有所增加,但这并不意味着滑移隔震结构隔震效果会不如普通的基础隔震结构,因为普通的隔震结构会产生摆动,摆动对结构的地震响应不容忽视。无论是否考虑碰撞,单体A 的地震响应随着摩擦系数的变化趋势基本一致,摩擦系数在0~0.03 变化区间,顶层最大位移随摩擦系数增加而减小,在摩擦系数在0.03~0.05范围内达到最小值,随后不断增加并逐渐稳定。而顶层最大加速度随摩擦系数的增加而不断增加并逐渐稳定。对于单体B,摩擦系数对位移响应影响不大,而加速度变化趋势与单体A相似。由此而知,摩擦系数越小,地震加速度响应越小,但当需控制结构位移响应时,建议摩擦系数在0.03~0.05范围内取值。
2.4 碰撞刚度的影响
在Hertzdamp 模型中,碰撞刚度不仅影响到碰撞力的大小,同时还会影响到碰撞期间的能量耗散。由于碰撞刚度大小和两相邻建筑物材料的性质有很大影响,所以研究碰撞刚度对结构响应的影响,对设计碰撞措施以及减小碰撞反应有很大的意义。假设其他条件不变,随碰撞刚度的变化,得到P-F滑移隔震结构和R-FBI滑移隔震结构两种情况下的结构顶层最大位移、最大加速度的变化曲线,如图6 所示。由图6 可以看出,当碰撞刚度为0,即不发生碰撞时,R-FBI 滑移隔震结构的隔震效果比P-F 滑移隔震结构明显。随着碰撞刚度的增大,单体A 的结构顶层最大位移会逐渐变小,随后逐渐趋于平稳,此时相邻建筑的限位作用得到明显体现,然后随着碰撞刚度的继续增加,碰撞力加大,单体A 的结构顶层最大位移会在一定区间内变化,且变化区间的最大值不断增加,而单体B 的结构顶层最大位移变化不大。单体A 的顶层加速度随着碰撞刚度的增大,呈正比例关系,即碰撞刚度越大,碰撞力越大,结构的加速度响应也越大。而单体B 在碰撞刚度较小时,顶层最大加速度不会随碰撞刚度变化,当单体A 的加速度达到和单体B 基本一致时,此时碰撞刚度到达临界值,单体B 也开始与单体A 一致,与碰撞刚度呈正比例关系。

图5 顶层位移,加速度随摩擦系数变化曲线(R-FBI隔震结构)Fig.5 Displancement,acceleration on top floor varying with coefficient of friction(R-FBI isolated structure)
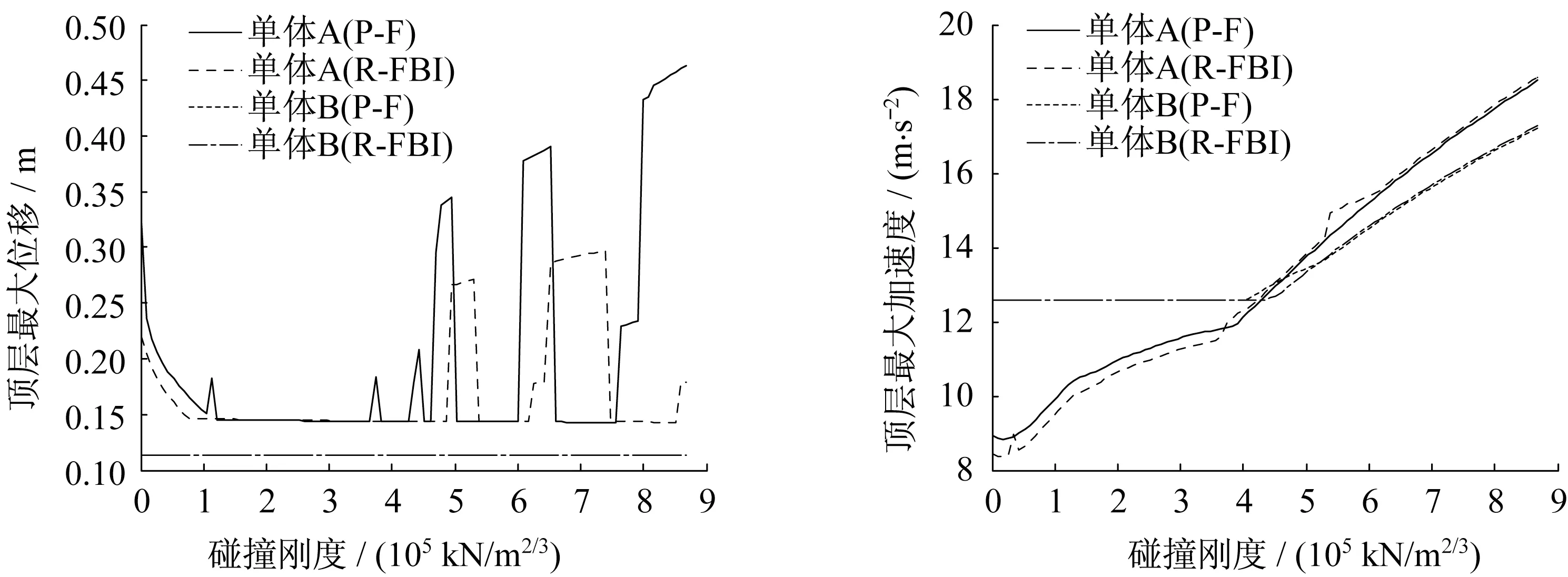
图6 顶层位移,加速度随碰撞刚度变化曲线Fig.6 Displancement,acceleration on top floor varying with collision rigidity
3 结 论
通过以上计算与分析,可以得出如下结论:
(1)当滑移隔震结构与相邻结构发生碰撞时,由于碰撞力的作用,结构的加速度响应会有所放大,而位移响应在碰撞力较小时会有所减小,碰撞力较大时放大;碰撞同时会造成层间位移有较大增加,由于滑移层的存在,碰撞对底部剪力的影响较小;无论结构是否发生碰撞,R-FBI 滑移隔震都比P-F滑移隔震隔震效果好。
(2)滑移隔震结构较普通的框架结构,预留的防震缝应更大,碰撞对滑移隔震结构的影响比普通框架结构的作用更大。
(3)摩擦系数越小,地震加速度响应越小,但当需控制结构位移响应时,建议摩擦系数在0.03~0.05范围内取值。
(4)碰撞刚度越大,结构的响应越大。在实际工程中,应采取降低结构碰撞刚度的措施。
