大型油罐罐壁损伤识别研究

2020-04-21徐晨光徐宏文

结构工程师 2020年1期

周奎徐晨光徐宏文

（上海理工大学环境与建筑工程学院，上海200093）

0 引言

我国在石油化工领域有大量大型储油罐。储油罐服役结束后，为解决废弃油罐的处理问题，可将其改造成公共建筑，从而使其继续发挥经济效益。储油罐在服役期间由于外部环境和内部荷载的作用，很容易造成腐蚀和损伤。因此，在改造之前需要对结构进行损伤检测，为后面加固改造提供依据。

传统的钢结构无损检测方法主要包括超声检测、射线检测、磁粉检测等。这些检测技术一般只能对小型结构或结构的某些部位进行检测，而且需要事先确定损伤的大体位置。同时所使用的设备仪器昂贵，检测费用较高，会受到场地、仪器的限制难以对结构进行实时的检测［1］。

目前，国内外学者对采用动力特性进行结构损伤识别的方法进行了大量的研究［2-6］。结构动力特性是结构的固有特性。结构的损伤会引起结构物理参数的改变，如刚度、质量、阻尼等，这些物理参数的改变又将导致结构动力特性的改变，如固有频率和模态振型的改变。利用完好状态下结构的动力参数与损伤结构的动力参数进行比较，从而判断结构有无损伤以及损伤位置和程度。

Pandey 等［7］首先提出利用结构损伤前后振型曲率变化的绝对值来判定损伤，并对简支梁和悬臂梁的损伤进行了研究，结果表明利用模态曲率比模态位移对损伤更加敏感。文献［8-12］阐述了模态曲率差法的可行性，但这些研究主要局限于对一维梁和二维平板的研究。

油罐罐壁属于薄壁圆柱壳结构，目前将模态曲率差法运用到薄壁圆柱壳结构的研究的文献并不多。本文采用模态曲率差法对油罐罐壁进行损伤识别仿真模拟研究，以实际工程上海西岸油罐艺术中心某废弃油罐为例，建立足尺有限元模型，研究该方法对油罐罐壁不同损伤工况的识别效果。该废弃油罐现场照片如图1所示。

图1 废弃油罐照片Fig.1 Photo of the abandoned oil tank

1 损伤识别指标

由弹性力学相关知识可知对于二维板壳结构的x，y方向的内力分量为

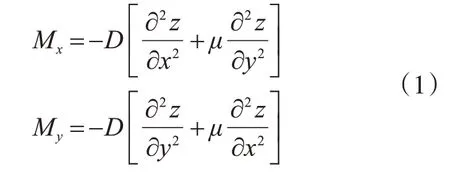
式中:z=z(x'y)为板壳结构法向方向位移曲面；D=[E(x'y)h3]/[12(1-μ2)]为板的弯曲刚度；E为弹性模量；μ为泊松比。

板在x'y方向的曲率为

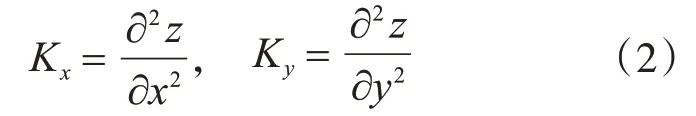
将式（2）代入式（1）可得:

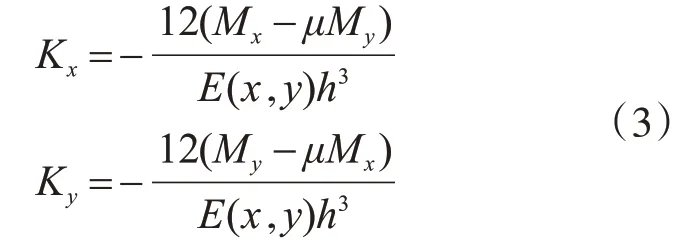
假定损伤后结构的内力重分布对Mx，My的影响很小，可以忽略不计。则曲率值K与弹性模量E和板厚h有关。

油罐服役期间，会因为腐蚀作用，使得管壁变薄，从而弹性模量减小。由式（3）可知，结构在损伤处的曲率与弹性模量和厚度成反比，当结构存在损伤时，损伤处的曲率增大，因而可以利用模态曲率来进行油罐罐壁的损伤识别。

由于油罐罐壁为薄壁圆柱壳结构，故采用柱坐标进行数据分析计算。得到罐壁径向模态振型后，忽略罐壁周向原始曲率，将罐壁展开成平板结构，油罐罐壁的周向为x坐标，轴向为y坐标，各节点的径向模态位移为z(x'y)。

根据公式（2），同时采用二次差分的方法近似得到x和y方向的模态曲率［7，13］:

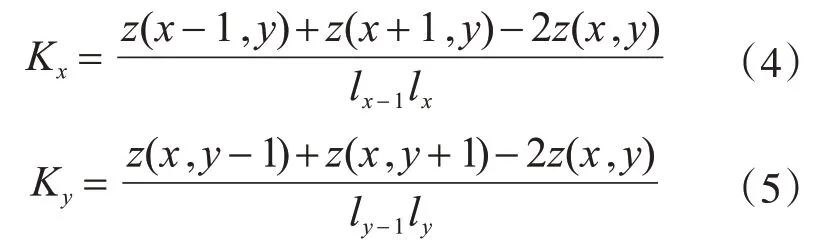
式中:lx为第x个单元周向弧长；ly为第y个单元轴向长度。

由于周向本身存在曲率，而式（4）并没有考虑其本身曲率的影响，因此其计算结果并不是真正的周向模态曲率，但由于公式简单，所以验证该损伤因子的损伤识别效果具有一定的实用意义。

以结构损伤前后模态曲率的差值的绝对值作为结构的损伤指标来进行损伤识别［14］。其损伤指标为

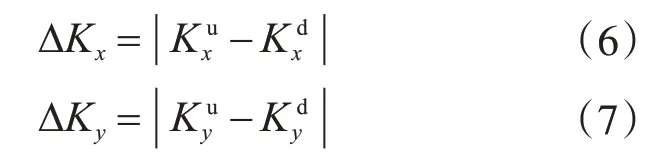
2 大型油罐罐壁损伤识别数值模拟

2.1 有限元模型建

上海西岸油罐艺术中心某油罐罐壁高12.48 m，内径为23.68 m。根据实际尺寸利用有限元分析软件ANSYS建立足尺模型。模型采用shell181单元，密度为7 850 kg/m3，弹性模量为2.06×1011Pa，泊松比为0.3，有限元模型周向划分60 个单元，轴向划分34 个单元。储油罐罐壁的厚度从下到上是依次减小的，共分为8 段，每一段的高度和壁厚如表1所示。

图2 油罐罐壁有限元模型Fig.2 Finite element model of oil tank wall

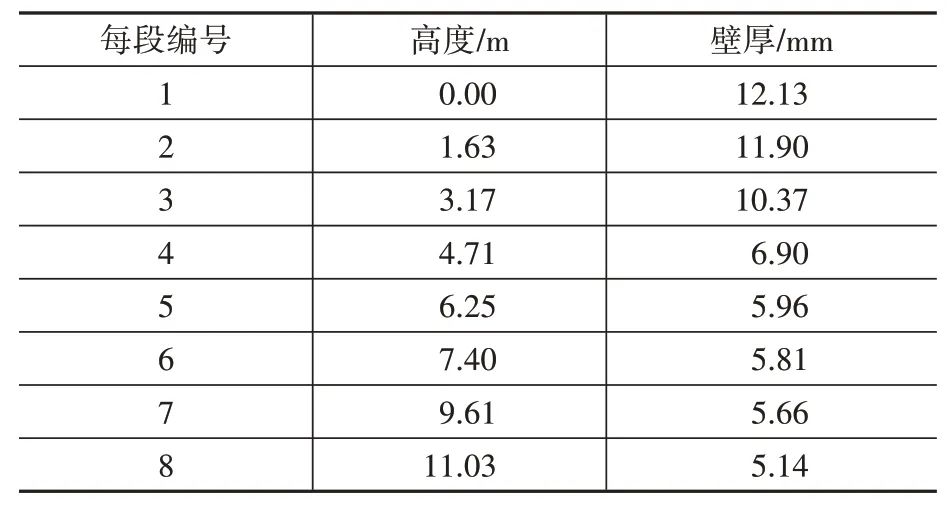
表1 油罐罐壁分段高度及壁厚Table 1 Height and thickness of every section of tank wall

2.2 损伤工况设计

油罐在长期服役期间，罐壁难免受到锈蚀以及液体腐蚀导致局部罐壁变薄。有限元模型通过改变单元的厚度来模拟损伤，分别研究单处损伤程度、不同高度的损伤和多处损伤的识别效果。损伤单元的位置如图3 所示，表中（x，y）坐标值分别表示周向的角度和轴向的高度。损伤工况分为三种，工况1:单处不同损伤程度，取单元2 模拟5%、10%、20%、30%程度损伤；工况2:单处不同高度损伤，取单元1 至单元4 模拟20%程度损伤；工况3:多损伤，取单元2、单元4 至单元6 模拟20%程度损伤。

2.3 薄壁圆柱壳模态振型特点

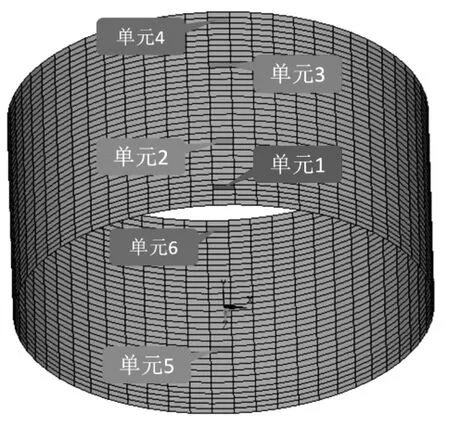
图3 损伤单元位置Fig.3 Locations of damaged elements

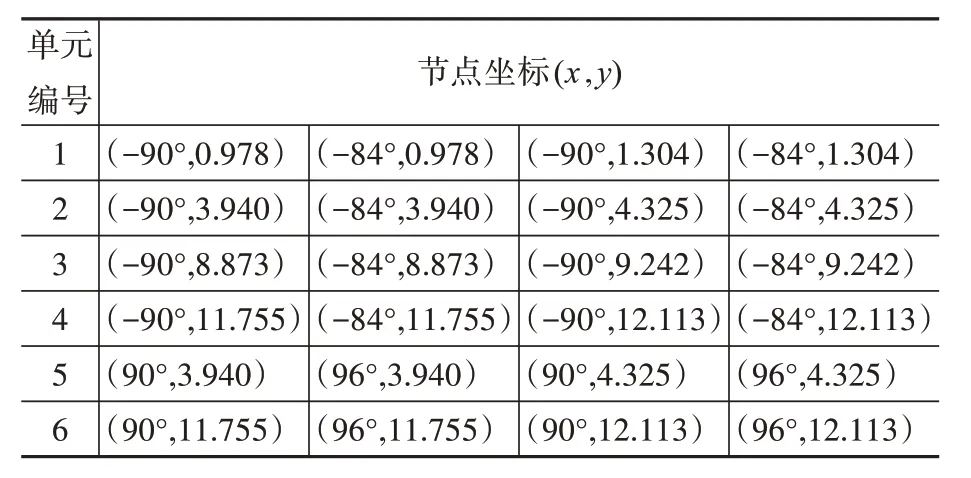
表2 损伤单元节点坐标Table 2 Coordinates of damaged element nodes

油罐罐壁属于薄壁圆柱壳结构，其振型一般包括轴向振型和周向振型。薄壁圆柱壳轴向振型与直梁的振型相似。对于一端固支一端自由且高径比较小的薄壁圆柱壳，振动主要表现为随轴向波数变化的周向模态振动，只有当频率较高时才会出现随轴向半波数变化的轴向振动。根据周向波数的不同，呈现出不同的花瓣模态（lobar modes）［15］。

2.4 罐壁损伤前后模态振型对应性

罐壁在无损时属于旋转对称结构，每一个固有频率都对应有无数个模态振型，它们在形状上完全相同，仅仅在角度上有所变化，换句话说，第k阶模态并不是唯一的，这就是“分离模态现象”［16-17］。

虽然无损结构的每一个固有频率对应着无数个模态振型，但ANSYS 有限元模拟只会给出一个振型。当模型发生损伤时该阶振型便是唯一的。也就是说，同一阶频率下，损伤前后的振型在形状上相似，即周向半波数和轴向半波数是一致的，但是它们的角度不一致。为了使得损伤前后的振型能够对应，需要对无损结构的振型角度进行旋转。根据振型一致时，各节点差值的和最小的原理来判断是否振型一致。利用MATLAB 编程序进行计算，具体算法步骤如下。

步骤1:得到无损结构和损伤结构的同阶模态振型，并按照节点位置排列成一个m×n阶的矩阵，m为轴向划分的节点数，n为周向划分的节点数。

步骤2:将无损模态振型矩阵A和损伤模态取值B两个矩阵中每个元素做差取绝对值得到矩阵C，然后求出矩阵C中所有元素之和，记为c。

步骤3:将矩阵A的第一列元素移到最后一列得到矩阵A1，然后用A1代替A，根据步骤2的算法，得到c1。

步骤 4:重复步骤 2 和步骤 3，得到c1，c2，…，cn，将其中最小值ci所对应的矩阵Ai作为无损结构的模态振型。

2.5 周向模态曲率差识别罐壁损伤

通过模态分析，采用柱坐标系，提取第一阶径向模态位移，根据式（4）可以得到周向模态曲率差ΔKx，然后利用MATLAB 三维绘图工具绘制三维曲面图。图4（a）是单元2损伤20%的周向模态曲率差曲面图，从图中可以发现周向模态曲率差损伤指标对损伤并不敏感。第一节模态振型轴向波数为11，由于波数太多，同时周向的单元数量有限，其仿真模拟的模态误差较大。通过计算前30阶的模态振型，发现第26阶振型的波数最少，为6个。通过计算得到其ΔKx曲面图，如图4（b）发现其相比第一阶模态能够较好的识别损伤位置，但在实际中难以得到高频率的振型。所以周向模态曲率差识别油罐罐壁存在着局限性。下文主要研究轴向模态曲率差ΔKy的识别效果。

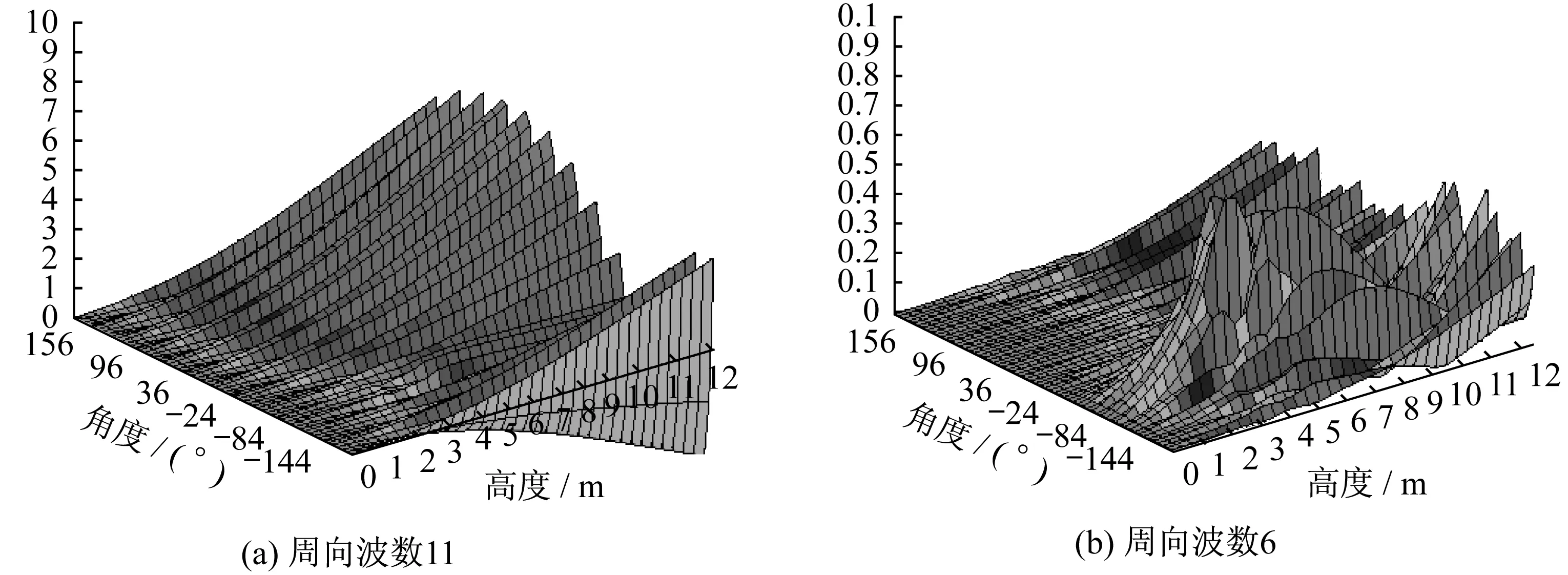
图4 不同周向波数周向模态曲率差（损伤20%）Fig.4 Difference of circumferential mode curvature for different circumferential waves（20%damage）

2.6 轴向模态曲率差识别罐壁损伤

1）工况1:单处不同损伤程度

通过改变单元2 的壁厚来模拟不同程度的损伤，比如损伤5%指的是这个单元的厚度减少5%。提取第一阶模态振型，根据式（5）计算得到轴向模态曲率ΔKy，并绘制三维曲面图如图5所示。

根据表2知道单元2所在位置为:高度范围为3.94～4.325 m，角度范围为-90°～-84°。图5（a）、图（b）、图（c）和图（d）显示的是单元2 不同损伤程度的轴向模态曲率差图，分析可知:四种不同损伤程度的轴向模态曲率图在预设的损伤位置均有明显的突变，可以精确判断损伤的位置；对比图中四幅图可以看出损伤程度越大，其损伤位置的突变就越明显。同时可以看出损伤程度越大其自由端的干扰就越明显。

2）工况2:单处不同高度损伤

分别在单元1 至单元4 设置损伤程度均为20%的损伤单元，结果如图6 所示，图中的不同高度值均指的是单元下端的高度值。

由图6 分析可知:图中轴向模态曲率差突变处均都是预先设定损伤的地方，更进一步说明了该方法能够运用到油罐罐壁的损伤定位当中；虽然损伤程度相同，随着高度的增加其模态曲率差的突变程度也会增加。

3）工况3:多处损伤

对单元2、单元4至单元6设计了4处损伤，损伤程度均为20%。其中2 处靠近自由端，且高度一致。另外2 处靠近固定端，且高度一致。其轴向模态曲率差图如图7所示。

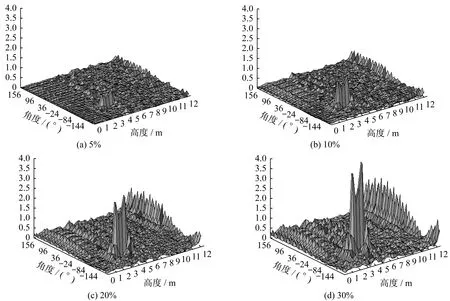
图5 单处不同损伤程度轴向模态曲率差Fig.5 Difference of axial mode curvature for different levels of damage at single location

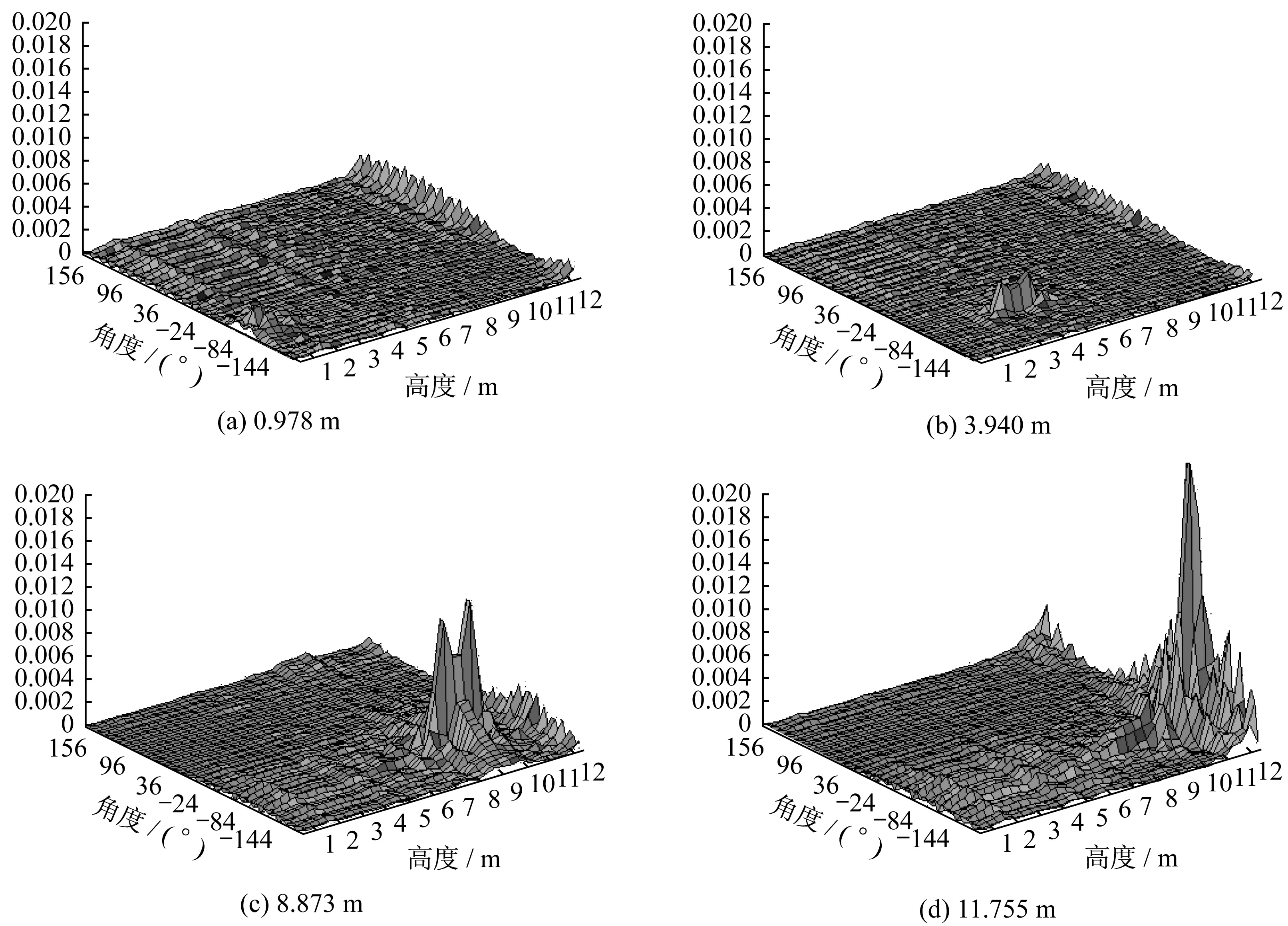
图6 不同高度损伤轴向模态曲率差（损伤20%）Fig.6 Difference of axial mode curvature for different levels of damage with single damage（20%damage）

分析图7 可知:图中轴向模态曲率差突变位置均为预先设定损伤位置；相同损伤程度下，相同高度的损伤，其轴向模态曲率差突变的程度基本一致，不同高度的损伤，靠近自由端的损伤，其轴向模态曲率差突变程度越大。

2.7 实际运用探讨

在通过有限元软件验证后，如何将基于模态曲率差的方法运用于实际的大型油罐中是值得探讨的问题。

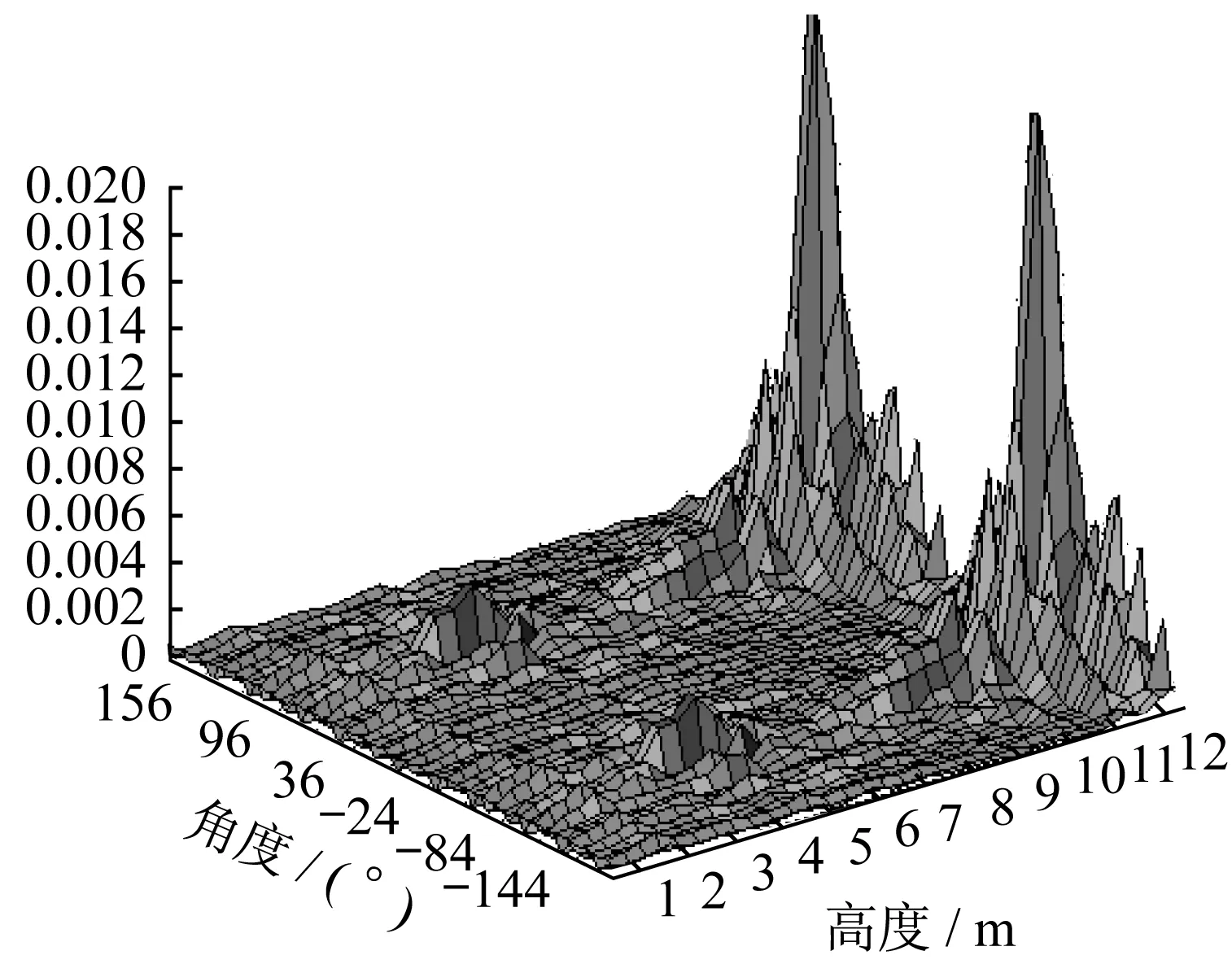
图7 多处损伤轴向模态曲率差（损伤20%）Fig.7 Difference of axial mode curvature with several damages

对于油罐这样大型的薄壁圆柱壳结构，由于结构过于巨大，以至采用单点激振时不能提供足够的能量，将我们所感兴趣的模态都激励出来；且结构具有对称性，会出现密集模态或模态重合。可采取多个激励来激发结构的振动，并同时采用多个响应传感器，即采取输入多输出（MIMO）方法。

在布置传感器时，可将传感器均匀布置在罐体四周顶端，采用锤击法添加激励，将罐体划分网格，用力锤依次锤击网格上点，通过传感器接收的信号计算出结构的模态。当前传统的传感器在进行这样大型结构的振动测试时传感器的布置确实复杂有难度，所以可以采用“先疏后密”的方法。在进行损伤检测时，首先要确定结构是否有损伤，所以在布置传感器时可以先采取间隔大一点的方式进行布置。如结构无损伤，则不需要进行下一步的检测；若出现损伤，可将初步检测结果中的损伤大致位置处的传感器进行加密布置，再次进行检测以获得准确的损伤位置。

随着检测仪器技术的快速发展，将无线技术的引入传感器中，对于油罐这样的大型结构，检测会更加的方便。