中国银行间市场国债收益率曲线：基于静态插值模型的估计

郭 枫 倪婧钰

一、引言

随着我国利率市场化改革不断深入，央行逐步放松对存贷款利率的管制，市场化利率也正逐步形成。十八届三中全会刊发《中共中央关于全面深化改革若干重大问题的决定》，其中首次提出“加快推进利率市场化，健全反映市场供求关系的国债收益率曲线”的新要求。在此大背景下，根据债券二级市场价格估计利率期限结构的可行性和实用性逐步增强。国债利率期限结构能最直接反映资产的无风险基础价格和市场资金的供求状况；国债收益率曲线形态的变化还可以进一步传递金融市场信息、预测宏观经济周期波动。因此，研究如何更好地拟合中国国债收益率曲线具有重大的现实意义。

国债收益率曲线反映不同期限无违约风险收益率之间的关系，其图像是在以期限为横轴、收益率为纵轴的坐标平面上描述的一条曲线。这里的“收益率”指即期收益率(spot yield/zero-coupon yield)、平价收益率(par yield)和远期利率(forward rate)。它们均由贴现函数导出，彼此之间可以相互转换。贴现函数的估计则基于债券市场各券报价或成交价格。由于任何债券市场的流通可交易债券在期限上均是离散的，无论贴现函数还是上述三种收益率函数均无法通过市场价格直接观测，必须从可观察到的各债报价中估计出隐含的连续利率期限结构。众所周知，无风险收益率曲线是金融市场资产定价的基准。因此，国债收益率曲线的拟合无论对科研学者还是金融从业人员来说都至关重要。

利率期限结构模型一般分为静态模型和动态模型。静态模型指采用插值(interpolation)等曲线拟合方法，利用某一债券市场(例如国债市场或AAA企业债市场)可观测到的债券报价或实际交易价格平滑拟合出该市场的贴现函数δ(m)。国外学者Fama和Bliss(1987)[1]、McCulloch(1975)[2]、Nelson和Siegel(1987)[3]、Fisher等(1995)[4]的研究都是这种方法的代表，不同之处在于他们选择构建插值模型的函数形式不同。主流研究中有两类插值模型具有较好的拟合效果和经济学含义，在行业运用中也最为普遍：一类是McCulloch三次样条模型(McCulloch Cubic Spline)，另一类是基于指数衰减函数的Nelson-Siegel-Svensson模型。前者由McCulloch(1975)[2]首次提出，经不断优化，McCulloch和Kochin(2000)[5]提出了非参Quadratic-natural cubic spline(以下简称QNC)三次样条插值模型；McCulloch和Kochin(2000)[5]同时提出基于线性最小二乘的迭代估计方法，用于估计模型的未知系数。后者起源于Nelson和Siegel(1987)[3]提出的Nelson-Siegel(以下简称NS)模型，但应用更广的还是经Svensson(1994)[6]拓展的Nelson-Siegel-Svensson(以下简称NSS)模型。这类模型的系数估计一般直接采用无约束非线性最优化。Guo(2019)[7]在吸收二者优良特质的基础上提出了多指数衰减插值模型(Multiple exponential decay interpolation model，以下简称MED)。他从经济学理论含义和实证拟合效果两方面对比了MED、NSS以及基于QNC的改进模型Semi-natural cubic spline(以下简称SNC模型)。他发现MED模型不但(部分地)吻合Nelson-Siegel模型中因子的经济学含义(根据Diebold和Li(2006)[8]总结)，而且保留了SNC模型的非参属性，使模型对不同收益率曲线形态的适应性更强。实证结果显示，MED模型在拟合过去20年美国国债收益率曲线时显著优于NSS和SNC模型。

动态模型基于收益率服从某种动态随机过程的假设，模拟收益率随时间变化的动态规律。最流行的一类动态模型是仿射期限结构模型(Affine term structure model,简称ATSM)，由Vasicek模型(Vasicek,1977[9])和CIR模型(Cox等,1985[10])等单因子模型演化而来，并经Duffie和Kan(1996)[11]、Dai和Singleton(2000)[12]、Ang和Piazzesi(2003)[13]等将其发展完善。此类模型将收益率表示为少数服从动态随机过程的因子的线性函数，用仿射扩散过程刻画因子的动态变化，通过无套利条件分析得出债券价格的解。

在探讨中国债券市场收益率曲线的文献中，利用静态和动态模型的研究成果均很丰富。在静态利率期限结构模型方面，郑振龙和林海(2003)[14]选取2002年9月13日的中国银行间市场国债价格对我国的利率期限结构进行估计，将线性插值模型和二次样条插值模型进行对比。他们发现二次样条插值模型具有计算简便的优点，且适用于形状复杂的收益率曲线拟合。朱世武和陈健恒(2003)[15]选取2003年3月28日上交所15支附息国债收盘价拟合即期收益率曲线，对McCulloch三次样条模型和NSS模型进行了比较，发现NSS模型拟合程度更高，尤其是在曲线远端拟合方面优于McCulloch三次样条模型，更适用于我国交易所国债市场收益率曲线的拟合。郭涛和李俊霖(2007)[16]选取2005年7月至2006年6月上交所国债收盘价，分别采用McCulloch三次样条、指数样条和NS模型估计国债利率期限结构，实证结果显示NS模型拟合效果更稳定，具有更好的样本外(out-of-sample)拟合能力；而NSS的样本内(in-sample)拟合虽更好，但样本外拟合误差显著大于NS，说明NSS模型存在过度拟合(over-fitting)。周子康等(2008)[17]在NS和NSS模型的基础上构建出了NS修正模型(以下简称NSM)，并对2005年1月至2007年11月的上交所国债收盘价数据进行拟合，结果显示NSM模型拟合精度更高，价格误差更小，在多项指标表现上优于NS和NSS模型，更适用于中国交易所国债市场。

动态利率期限结构模型方面，范龙振和张国庆(2005)[18]构造了两因子CIR模型，选取1997年1月至2002年4月上交所国债交易价格数据进行估计，发现两因子模型不能充分捕捉收益率曲线形状特征，且预测误差具有系列相关性，模型的因子解释能力有待提高。沈根祥和陈映洲(2015)[19]在动态NS模型(Diebold和Li,2006[8])的基础上提出了双斜率动态NS模型，并选取2006年3月至2013年11月银行间市场国债数据进行拟合，结果显示双斜率动态NS模型对我国国债收益率曲线近端的静态拟合和动态预测效果较经典动态NS模型显著提高。丁志国等(2016)[20]选取2005年1月至2012年12月中国宏观经济数据作为状态变量，并将状态变量假设为AR(1)、AR(2)、ARMA(1,1)以及随机游走四种动态过程，然后比较拟合和预测效果。结果显示Vasicek-AR(1)模型更加适合中国国债收益率的拟合与预测。

静态利率期限结构模型因具有更简洁的函数形式、更小的计算负荷，以及比经典ATSM模型更好的拟合效果(Christensen等,2011[21])，在学术研究和行业实操中有着更广泛的应用。SNC和NSS两种主流的静态模型各有优劣，两者之间的选择在很大程度上取决于拟合收益率曲线的目的。SNC是非参模型，模型的具体参数个数可由样本数据最优决定，因而在拟合各种收益率曲线形态方面具有更大的灵活性，适合金融从业者寻找市场短期价格异象(price anomalies)及套利机会。遗憾的是，基于三次函数的SNC模型偶尔给被拟合的收益率曲线带来一些不切实际的形态；此外，模型还必须施加远端点条件(long-end point condition)，以便在远端点之外的外推区间(extrapolation)实现渐进收敛(asymptotic convergence)。反观之，NSS模型是参数模型，模型表达式是固定的，不能随样本数据优化调整，因而拟合的曲线形态相对单一。然而，NSS模型的基础指数衰减函数自带渐进收敛性，模型不需要施加任何端点条件；而且指数衰减函数天然适合拟合贴现函数曲线，这为收益率曲线提供了更简约的函数形式和更光滑平稳的拟合效果，因此更适合宏观经济学家将其用于科研目的。Guo(2019)[7]提出的MED模型继承了这两种代表性插值模型的优点：首先，MED基于指数衰减函数，继承NSS模型的简约性与拟合平稳性；其次，MED继承SNC模型的非参性，能适应更多的曲线形态。在美国国债市场收益率曲线的拟合中，MED模型的表现优于SNC和NSS，在一定程度上证明了MED模型的实用价值。

应用MED模型拟合中国国债收益率曲线，并检验其拟合效果是否更优将是一个有趣的研究课题。本文首次同时使用三种模型拟合中国银行间市场国债收益率曲线，在三种曲线拟合“赛马”的实验中对比研究MED、SNC和NSS的优劣。对于三种模型未知参数的估计，本文均采用McCulloch和Kochin(2000)[5]提出的迭代线性最小二乘估计法。对于非参模型MED和SNC，本文按照Guo(2019)[7]提出的参数选择最优化方法进行调整。具体地，模型参数的选择应同时满足以下两个条件：(1)拟合误差项为完全随机的白噪音序列。此条件由Durbin-Watson或其他序列相关检验确定。(2)模型整体拟合优度最优。此条件通过贝叶斯信息准则(Bayesian Information Criterions，简称BIC)确定。综合两项检验的结果选择最合适的参数个数和模型设定。我们选取2009年1月至2018年12月共计10年的银行间市场国债月度价格数据作为样本，每个月的数据由当月最后一个交易日的交易(或报价)数据代表。每一期月度(横截面)样本数据被分为样本内和样本外两个子样本集。样本内数据用于模型未知系数估计，样本外数据用于检验模型是否存在过度拟合。在残差分析中，我们选择加权均方根误差(weighted root mean squared error，简称wRMSE)衡量其拟合效果。由于MED和SNC是非参数模型，残差分析结果无法直接与参数模型NSS进行对比，我们因此对两个非参模型的价格残差统计量wRMSE进行标准化，并将原始和经标准化的wRMSE进行模型间比较。样本内和样本外两个组别的残差分析显示，MED在每个样本子集和绝大部分期限区间产生最小的标准化累计加总月度wRMSE、月度wRMSE极大值和标准差。这表明MED模型的曲线拟合优度最高，稳健性最好，而过度拟合问题却并不突出。

本文剩余部分安排如下：第二部分在基本定义的基础上回顾MED、SNC和NSS三种模型并进行定性对比；第三部分讨论插值模型未知系数的估计方法，并分别用三种模型拟合中国银行间国债市场收益率曲线；第四部分在残差分析的基础上比较三种模型在拟合中国银行间国债市场收益率时的优劣性及稳健性；第五部分为总结。

二、模型及设定

(一)基础变量及函数定义

收益率或债券定价的相关基本概念在此不加赘述，本部分主要统一文中各模型通用的变量及函数定义。

(1)

简单起见，我们假设国债的价格由公式(1)的离散现金流形式决定。对于附息型中国国债，离散现金流发生的频率为半年一次或一年一次。

在已知贴现函数的基础上，我们可以推导出债券市场的收益率。三大主要收益率中，连续复利即期收益率(spot yield/zero-coupon yield)(2)即期收益率也被称为即期利率或零息债到期收益率，其经济学含义为投资者对期限为m、没有任何中间现金流的一笔即期投资的收益回报需求。定义为：

(2)

中国债券市场上流通的国债类型可分为附息、零息和到期一次还本付息(发行期限为一年)三种。对于附息型国债，平价收益率(par yield/par bond yield)是另一类重要收益率指标，即期限为m的附息债券以票面价格出售时的到期收益率。连续现金流情境下的连续复利平价收益率定义为：

(3)

利率期限结构也可以用远期利率(forward rate)表示。这种收益率是投资者当期对未来特定时期——从m1年后开始，以m2年为期限——进行零息债投资的收益需求。当m2→0，我们得到瞬时远期利率(instantaneous forward rate)，即投资者当期要求的m年后的瞬时回报率。连续复利下的远期利率(3)本文从此处起将“瞬时远期利率”直接简称为“远期利率”，下文不再专门区分。可表示如下：

(4)

由公式(2)和公式(4)可推出

(5)

其中-logδ(m)的经济学含义为期限m年的总收益，而y(m)与f(m)分别是投资的算术平均收益和边际收益。由公式(3)和公式(4)又可知

(6)

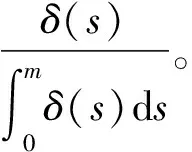
公式(2)～公式(6)表明，即期收益率、平价收益率和远期利率均可由贴现函数δ(m)导出，且任意两两间可相互转换。因此，收益率曲线拟合问题变成了一个贴现函数的建模问题。

(二)模型一般函数式

许多研究者选择针对负对数贴现函数-logδ(m)建立利率期限结构插值模型，而非直接建模贴现函数δ(m)。基于负对数贴现函数建模的优点是便于给插值模型施加端点条件。例如，SNC模型就施加了远端点自然条件，从而实现拟合目标函数在远端外推(extrapolation)区间单调递增(二阶导数在远端点收敛于零)。但这种建模方式的缺点在于贴现函数和债券价格函数的非线性会极大增加系数估计的计算负荷。

Guo(2019)[7]首次将所有插值模型归纳为基于负对数贴现函数建模的同一类一般函数式(general functional form)，不同模型之间的差异则体现在构成一般函数式的不同的基础函数(basis functions)。降低计算负荷、提高数值算法收敛稳健性通过将非线性估计转换为线性估计实现，例如使用McCulloch和Kochin(2000)[5]提出的迭代线性最小二乘法。此法在第三部分使用过程中将详细讨论。

根据Guo(2019)[7]的研究，负对数贴现函数的一般函数式φ(m)为：

(7)

该式将-logδ(m)假设为基础函数Ψ(m)和系数β的线性多项式组合，且必须满足两个条件：(1)φt(mt,i)通过原点；(2)在任意t时刻，多项式总项数kt不大于(用于估计的样本内)样本观测总数nt。

(三)模型基础函数式

1.MED模型。

MED(Multiple Exponential Decay Interpolation)模型由Guo(2019)[7]提出。模型基础函数式Ψj(m)遵循以下两个原则建立。其一，贴现函数δ(m)具备(近似于)指数衰减函数的特征：在近端具有向上、反向或驼峰的形状，在远端渐进衰减并收敛于0。其二，受ATSM等动态模型启发，y(m)被假设为服从某种动态随机过程，其函数表达式一般由微分方程构成；f(m)因此应该是指数函数，因为根据公式(5)，f(m)是微分方程y(m)的解。为了控制拟合收益率曲线远端的渐进收敛特性，MED模型表达式全部kt个基础函数Ψj(m)中应有一个的一阶导数为常数1，其余(k-1)个Ψj(m)的一阶导数收敛于0，而这(k-1)个Ψj(m)的原函数值应收敛于一个有限数值。如此，远期利率曲线和即期收益率曲线各自拥有一条远端渐近线(asymptote)。

综上两原则，MED模型的Ψ(m)被设定为：

(8)

其中，参数τj不随期限m变化，但随Ψj(m)变化。

由公式(2)可得即期收益率y(m)的表达式：

(9)

按照Diebold和Li(2006)[8]对NS模型经济学含义的解释，公式(9)最后一项βk代表NS模型中的长期“水平”(level)因子，用于拟合即期收益率曲线在m→时的收敛水平。剩余项系数与NS模型的短期“斜率”(slope)因子一致，决定了所拟合期限结构的期限利差。与NS模型不同的是，MED模型中没有第三种“曲率”(curvature)因子，取而代之的是额外的、不定数量的“斜率”因子。显然，MED模型部分地继承了NS(以及NSS)模型的因子，因此它们具有近似的经济学解释。

2.NSS模型。

NSS(Nelson-Siegel-Svensson)模型是由Svensson(1994)[6]在NS模型基础上拓展而来。Gürkaynak等(2007)[22]用远期利率函数定义的NSS模型表达式如下：

(10)

为了将公式(10)统一为公式(7)的形式，我们根据公式(4)将f(m)积分，得到NSS模型的一般函数式(7)，其基础函数表达式如下：

Ψ1(m)=m

(11)

NSS和MED的模型表达式有两个共同特征。其一，它们都基于指数衰减函数exp(-m/τ)，而这一函数在数学上定义了“e重衰期”(e-fold life)(4)e重衰期的定义类似于半衰期(half life)，指一个整体衰减至其最初大小的1/e所需的时间。。其二，它们包含两个共同因子：水平和斜率。然而，它们在拟合收益率曲线的灵活性上有很大差异。对于NSS，k的取值固定为4，即有6个未知参数需要估计——4个β和2个τ。因此，它最多能拟合两个“驼峰”的收益率曲线。相比之下，MED模型允许任意正整数k的取值，以便为拟合的收益率曲线提供同等甚至更丰富的形状。这一特性大大提高了模型的拟合灵活性。

3.SNC模型。

SNC(Semi-natural cubic spline interpolation)模型是Guo(2019)[7]在McCulloch和Kochin(2000)[5]QNC(Quadratic-natural cubic spline interpolation)模型基础上扩展而来。QNC模型对近端(第一、二个节点间)施加了一个二次型端点条件，而在远端(终节点之外)施加了一个线性自然条件，故名Quadratic-natural。然而，Guo(2019)[7]认为在样本量足够的情况下，近端的二次型条件既无理论基础，又缺乏经验证据，而且在模型估计过程中显得多余，完全可以舍去。因而Guo(2019)[7]提出SNC模型，舍去近端二次型条件，保留远端的自然条件，其余跟QNC基本保持一致(5)其实SNC模型相较QNC在节点选择、k值确定等方面还有显著不同。Guo(2019)[7]有详细讨论，此处不再赘述。。该模型的基础函数被定义为如下三次函数族，目的是在每个节点周围二阶连续且光滑。

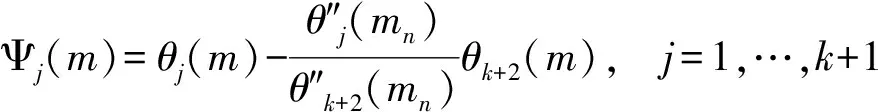
(12)

其中：θ1(m)=m,θ2(m)=m2,θ3(m)=m3,θi(m)=max{0,(m-κi-2)3},i=4,…,k+2。

MED与SNC都属非参插值模型，kt取值随t期样本数据变动。这一特性使得MED与SNC模型在拟合收益率曲线时具有比NSS模型更大的灵活性。遗憾的是，基于三次函数的SNC模型偶尔给被拟合的收益率曲线带来一些不切实际的形态，例如过分“弯曲”或过多“驼峰”的曲线。此外，在远端外推区间，三次函数无法自主实现渐进收敛，必须专门施加约束条件，如SNC模型中的线性自然条件。施加线性约束条件后，即期收益率函数在外推区间获得渐进收敛，但远期利率函数自终节点(6)终节点一般由用于估计的样本券的最长剩余期限确定。起将变为常数。这有悖利率期限结构的无套利条件(7)尽管实际操作中，这种套利机会可能无法实现，因为国债市场上找不到剩余期限长于终节点所对应期限的个券用于套利。不过，无风险收益率曲线是金融市场资产定价的基准，它可能被用于国债市场以外的其他市场，任何期限因此都有可能成为定价标的。。相比之下，MED模型基于指数函数，所拟合的曲线更加平滑；此外，指数衰减函数自带收敛特性，不需要添加任何约束条件，这也是MED模型较SNC的先进之处。

综上，从定性分析角度而言，MED相较于另外两个模型更具优势。与SNC相比，MED模型具有更强的拟合稳定性，且不存在因端点约束条件导致的套利机会。与NSS相比，MED模型在拟合各种类型收益率曲线方面具有更大的灵活性。

三、模型估计及实证结果

解决该问题的有效途径之一在于将非线性最优化转化为迭代循环的线性优化问题。Guo(2019)[7]比较了一般的非线性最优化估计方法和基于McCulloch和Kochin(2000)[5]的迭代最小二乘估计法(iterative linear least squares,简称ILLS)，发现在拟合美国国债市场数据时，ILLS在高效性和稳健性两方面均有压倒性优势。本研究因此直接摒弃非线性最优化，而统一将ILLS运用于三种模型对中国银行间国债市场收益率曲线的拟合。本部分首先简要回顾ILLS估计方法与非参数模型的最优设定，然后汇报三种模型对中国国债收益率曲线拟合的实证结果。

(一)模型估计方法

我们选取2009年1月至2018年12月共计10年(120个月)的银行间国债市场月度数据作为样本，所有数据取自Wind.月度数据以样本期间每个自然月最后一个交易日的数据为准。每个横截面样本包括当天所有流通券中有交易或有报价并进行一定剔除后的债券，例如剔除所有含权券和有特殊流动性问题的个券。对于保留下来的样本券，我们收集它们的发行期限、到期日、息票率、付息频率、加权平均买卖净价、交易金额(如果有)等指标数据。然后，对这些数据进行预处理，并将每个横截面样本分为样本内(in-sample)和样本外(out-of-sample)两个子样本，每个子样本集的观测点数量约占筛选后整体样本的50%。其中，样本内子集用于模型估计，而样本外子集用于模型比较。涉及样本券选取、数据预处理和样本分组的具体方法在附录中详述。

正常的参数估计步骤应该是首先确定k值，即(非参数)模型的具体表达式，再进行β和τ的估计。不过，本部分在假设k取值确定的情况下首先介绍如何基于ILLS估计τ和β，然后再讨论选择最优k值的方法。

1.τ的设定。

不同于Gürkaynak等(2007)[22]整体估计未知参数β和τ，Guo(2019)[7]选择基于样本内子集的剩余期限分布直接赋值τ，然后根据τ值再估计β。直接赋值可以进一步降低计算负荷，提高估计效率。不仅如此，直接赋值τ也有一定理论基础。依上节分析，MED和NSS模型均基于指数衰减函数exp(-m/τ)，其决定了所拟合曲线的斜率和曲率，而斜率和曲率出现变化的位置由τ的取值决定：τ取值较小时，收益率曲线形态在较小的期限区间(近端)产生变化，反之则在较大的期限区间(远端)产生丰富的形态。中国国债市场流通券的剩余期限分布一般特点为中期(1～10年)最多，短期(1年以下)次之，长期(10～50年)最少，因此收益率曲线形态变化与丰富程度的分布也应该跟上述剩余期限分布大致吻合。

步骤Ⅰ：令τk→，使得Ψk(m)=m，βk因此控制远期利率f(m)在远端(m→)的渐进收敛。

2.β的估计。

(13)

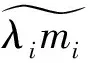
步骤Ⅰ：加权线性最小二乘法(WLS)估计β0，权重为各债券成交金额占当日市场总成交额的比例。其中ytmi是债券i的到期收益率(10)由于债券价格取买卖全价的平均价，这里的到期收益率即是按全价均价计算的到期收益率。：

i=1,…,n.

(14)

(15)

步骤Ⅲ：运用WLS估计βq+1：

i=1,…,n.

(16)

3.k的选择。

Durbin-Watson(以下简称DW)是检验拟合残差是否存在序列相关的候选方法之一。以拟合2015年7月银行间国债市场收益率曲线为例，图1展示了MED模型在不同k取值时拟合残差项的DW统计值及其95%置信区间(11)具体来说，从k=2开始获得模型每个k值对应的DW统计数据。基于k值的载荷矩阵ψ(m;τ)，对95%置信区间和平均临界值进行数值模拟，并将它们分别点绘在图上。。如图所示，DW统计值大致随k增大而增大；95%置信区间给出拟合残差项不存在序列相关的DW值范围。第一个超过左尾2.5%下界(图1中的点划线)的DW值对应最小k值，即k=3，该k值的MED模型拟合残差项不存在序列相关。该k值对应的DW值同时也最接近其平均临界值(图1中的虚线)，这样的k确保了残差项出现序列相关的概率最小。

图1 DW检验结果,2015/07,MED

注：(1)运用MED模型拟合2015年7月31日收益率曲线，此图显示模型每个k≥2整数值对应的DW统计值。(2)2015年7月31日样本内子集债券数量=23，样本外子集债券数量=22，样本总量=45。(3)95%置信区间和平均临界值已在图中给出，基于单尾检验。

然而，DW检验所基于的强假设在一定程度上限制它在本研究中的应用。首先，DW检验假设残差项为正态分布，且不适用于高阶自相关。其次，DW检验对样本量和k的取值有一定适用要求。当这些假设条件不完全满足时，非参数游程检验(non-parametric run’s test)可以作为检验序列相关的另一个候选方法。它用于检验一个双值序列的相互独立性，原假设为序列中的元素是随机的。在我们研究的问题中，残差项的“游程”(run)是序列的最大非空段，该序列由0值上下的连续元素组成。游程检验返回的伴随概率可与预先设定的显著性水平(例如5%)进行比较，以判断是否拒绝原假设。与图1所示的DW检验类似，我们依次对k≥2的每个整数k值进行游程检验。第一个伴随概率大于5%的k值确定了最简洁的非参模型表达式。

对于模型整体拟合优度，我们可以运用各种信息准则挑选最优k值。以贝叶斯信息准则(Bayesian Information Criterion，简称BIC)为例，图2显示了2015年7月收益率曲线拟合中每个k≥2整数值对应的BIC值。其中，BIC值随k值先降低后上升，当k=4时模型拟合优度最高；k=3或5的拟合优度次之。

图2 BIC结果,2015/07,MED

注：(1)运用MED模型拟合2015年7月31日收益率曲线，此图显示模型每个k≥2整数值对应的BIC值。(2)2015年7月31日样本内子集债券数量=23，样本外子集债券数量=22，样本总量=45。

综合上述序列相关检验和模型整体拟合优度，用MED模型拟合2015年7月银行间国债收益率曲线时，我们为模型取值k=3。在本例中，根据DW检验结果，选择k=3确保了残差项序列相关的概率最小，同时保证了模型最简约。虽然最优BIC值对应k=4，但其DW检验结果靠近右尾2.5%上界(图1中的实线)；而且，k=3对应的BIC值也基本接近于k=4对应的BIC值。以DW检验结果为主要参考，结合BIC值，我们因此选择k=3作为该月k的最终取值。

在样本期内，我们为MED和SNC模型分别选择每个横截面样本最适合的k值。表1的C组给出了样本期内k值选取的统计分布。

(二)实证结果

按照第三部分第一节的方法，我们尝试用MED、SNC和NSS三种插值模型分别对每个月度的收益率曲线进行拟合。图3是基于2015年7月银行间国债数据进行拟合的收益率曲线。基于相同横截面样本，三种模型的拟合结果差异十分显著。首先，SNC模型拟合(图3-(b)所示)的远期利率曲线(虚线)在终节点(12)据Wind数据显示，2015年7月31日银行间国债市场有交易或双边报价的债券中期限最长为9.95年。该期限自然成为2015年7月收益率曲线拟合样本的终节点。之后的远端外推区间变为水平。这是线性自然端点条件作用的结果，也是套利机会产生的来源，而其他两个基于指数函数的模型没有出现这种情况。其中，MED模型的远期利率曲线(图3-(a)所示)实现收敛，而NSS(图3-(c)所示)不仅未明显收敛，还出现收益率在远端变为负值的情况，跟现实情况不符。其次，三个模型拟合的远期收益率曲线均有一个驼峰，但出现的位置不同：NSS模型大概出现在第6～7年，而另外两个模型大概在5年的位置。最后，MED和NSS模型拟合的即期收益率曲线(实线)均出现顶点(虚线向下穿过实线之处)，然后MED的远期利率曲线自顶点处单调收敛，NSS模型的远期利率曲线没有任何单调特征；SNC模型拟合的即期收益率曲线在50年内没有顶点。

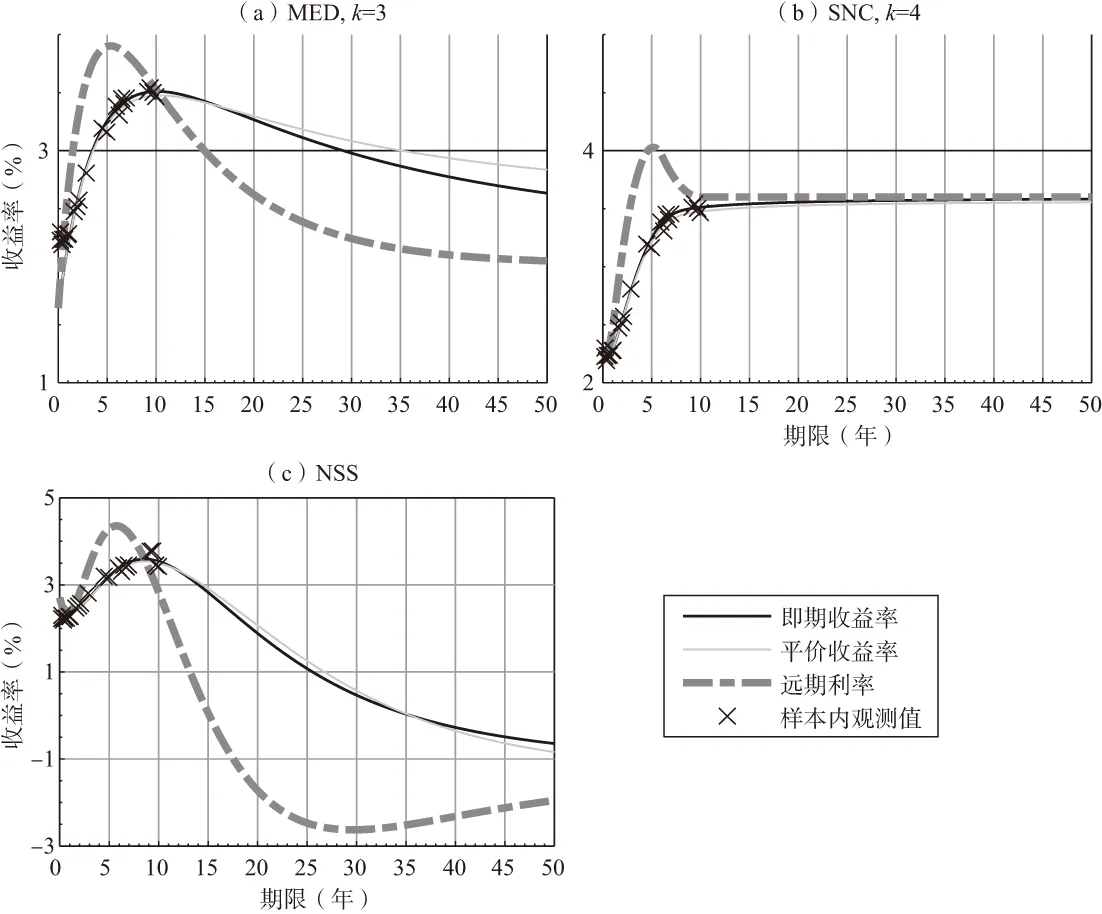
图3 拟合的收益率曲线,2015/07

注：(1)图(a)、(b)、(c)显示的收益率曲线分别由MED、SNC、NSS模型进行拟合。(2)期限以年为单位，收益率以年百分比表示。(3)样本取自中国银行间国债市场2015年7月末有成交或报价的数据。

图4展示三种模型分别拟合样本期全部120个月的月度即期收益率曲线，从中我们可以看到近10年来中国无风险收益率曲线随时间变化的动态过程。图4-(a)为MED模型拟合的收益率曲线，该拟合成功地捕捉到样本期初的低利率环境以及2013和2017年两次“钱荒”事件导致的利率高企。具体而言，2008年金融危机发生后，全球进入货币政策宽松期；当时我国实施积极的财政政策和适度宽松的货币政策，刺激投资、扩大需求。在这种政策背景下，2009年及其之后一段时间的资金成本走低，体现在短期和长期的无风险利率大幅下行。2013年，信用大规模向地产、地方投融资平台等部门扩张，银行资金被贷短长用的期限错配现象严重；央行随即控制资金投放，导致市场(特别是货币市场等短期市场)资金全面紧张，国内出现流动性收缩，短期利率也随之攀升。2017年市场情况与2013年类似，同样是由于“钱荒”引起利率攀升，在图中可明显看到那时的利率处于较高水平。除此之外，图4-(a)还显示在过去10年里个别月份即期收益率曲线出现水平甚至倒挂，预示当期宏观周期出现转折。

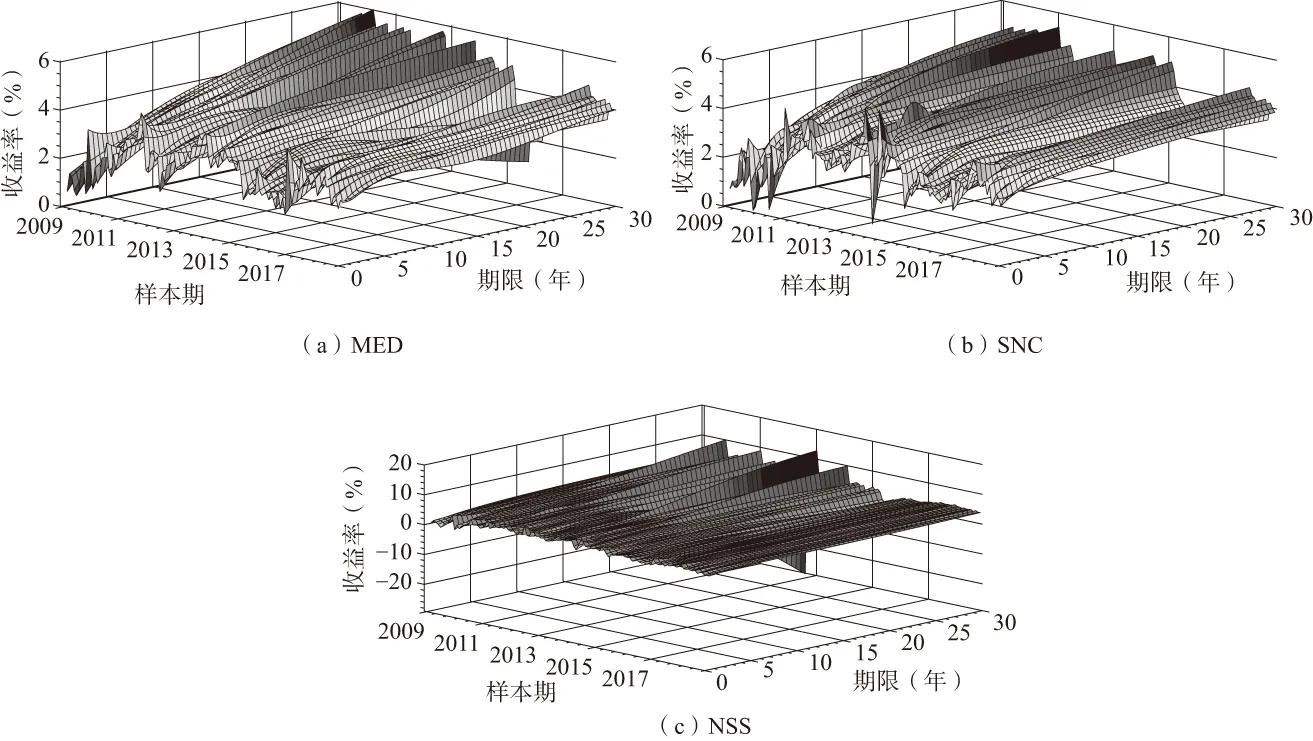
图4 拟合的即期收益率曲面,2009/01—2018/12

注:(1)图(a)、(b)、(c)显示的三维曲线分别由MED、SNC、NSS模型进行拟合。(2)期限以年为单位；收益率以年百分比表示。(3)共选取样本期中国银行间国债市场120个月的月末报价数据。

相比之下，SNC和NSS模型的拟合结果(图4的(b)和(c)所示)不能清晰、完整地反映收益率曲线的动态变化过程，特别是NSS模型的拟合曲面严重扁平化。出现此情况的主要原因是NSS模型在个别月份未能成功地在远端实现收敛，导致收益率纵轴(Yield)被放大，无法体现曲线在局部收益率区间的复杂波动，说明其在拟合中国银行间国债市场数据时的收敛稳健性较差。SNC模型在远端表现较好，但近端出现异常波动，对利率环境特征的捕捉力不足。在下一节中，我们将进一步对比MED模型与其他两模型拟合的优劣性与稳定性。

四、模型定量比较——基于残差分析的“赛马”实验

表1 残差分析和模型设定的描述性统计汇总

(一)残差分析标准化

收益率曲线拟合最不能忽视的问题是过度拟合，即通过增加非参数多项式模型的项数或参数个数达到样本内更好的拟合结果。这样做往往无法在样本外获得同样成功的拟合。因此，我们将每个横截面样本整体分为样本内和样本外两个子样本，目的就是要对比同一个模型在样本内与样本外拟合的差异，特别要检查样本内拟合优度最高的模型是否在样本外也能实现最高的拟合优度。

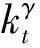
(17)

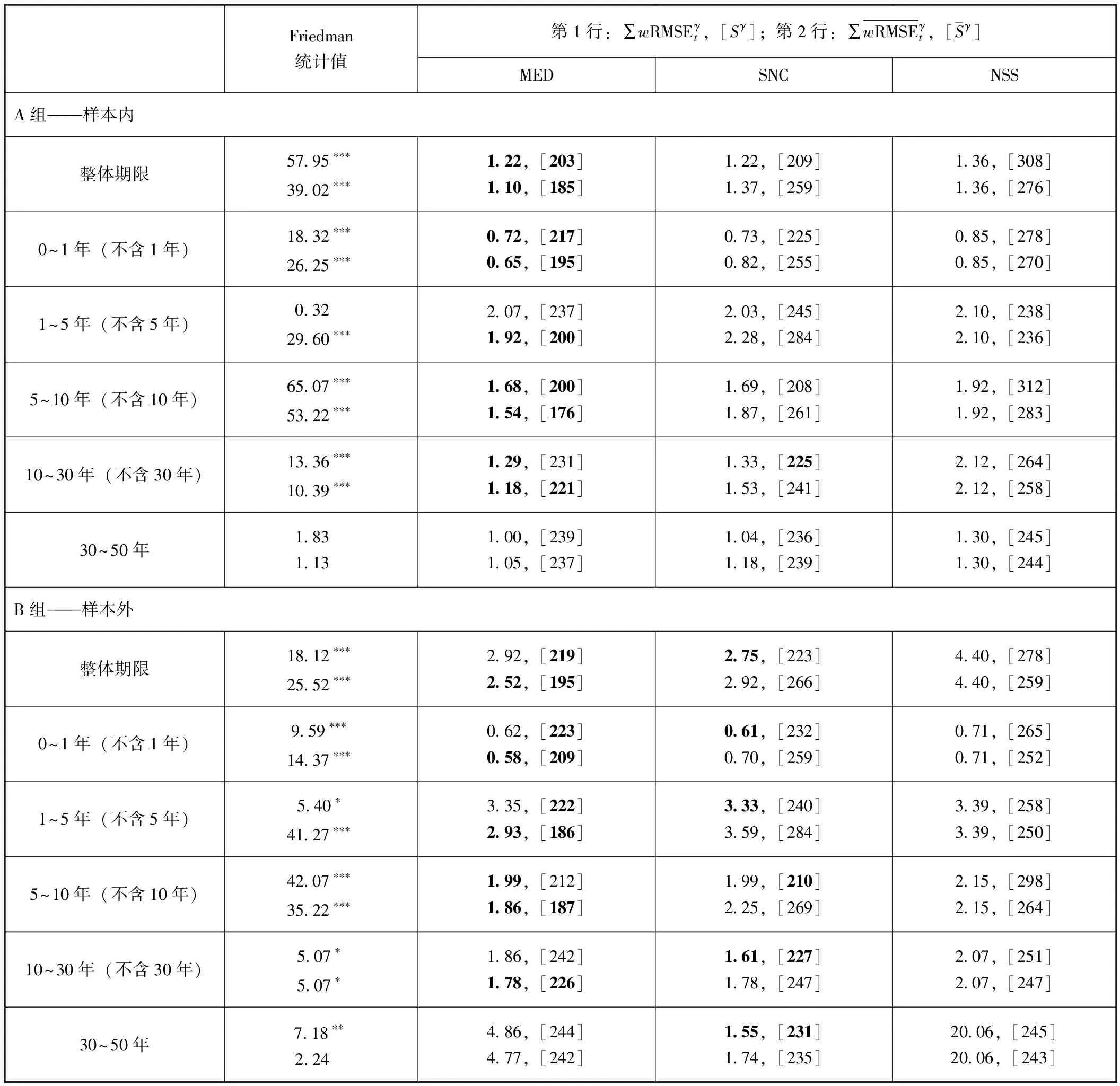
表2 月加权RMSE累计总和，2009/01—2018/12

(二)中国国债市场的拟合结果

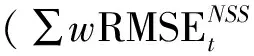
综上所述，基于中国国债市场现状，MED模型在样本期比其他两个模型具有更好的拟合性能，且过度拟合程度最低。因此，MED模型在中国银行间国债市场有更好的应用价值。与此同时，我们也验证了SNC模型和NSS模型在应用上的优势和局限：SNC模型虽然存在过度拟合的情况，但同样具有不错的拟合效果，在某些情况下可作为收益率曲线拟合的备选模型；而NSS模型表现明显弱于其他两个模型，不推荐将其运用于中国银行间国债市场。

五、结论

本文着眼于利率期限结构静态插值模型，重点研究适用于中国银行间市场国债收益率曲线拟合的实证模型。在研究中国债券市场的文献中，本文的亮点有三。首先，本文首次将MED模型引入中国市场，尝试用其拟合中国无风险收益率曲线。其次，本文摒弃稳健性和计算效率均不佳的非线性最优化估计法，转而采用McCulloch和Kochin(2000)[5]提出的迭代线性最小二乘法进行未知系数估计。最后，按照Guo(2019)[7]提出的参数选择最优化方法对非参模型进行最优调整，即通过DW检验或其他序列相关检验确保拟合残差项为白噪音序列，并结合BIC值确定模型整体拟合优度。综合两项检验的结果，同时考虑模型的有效性、最优性和简约性，逐期选择最合适的参数个数和模型具体设定。

附录

数据预处理及样本分组

中国银行间国债市场数据源自Wind金融数据库。在进行估计之前，需要对数据库原始数据进行筛选、分组和预处理。首先，计算附息国债的到期收益率，此处计算使用的债券价格为加权双边买卖均价净价计算出的相应全价(dirty/full price)。考虑到中国国债存在半年付息一次与一年付息一次两种息票现金流形式，我们分别将计算出的不同离散复利到期收益率A转换为连续复利到期收益率R：

接下来对数据进行筛选，建立样本池。首先，对于发行期限在一年以下(不包括一年)的零息债券，全部包含在样本池中。其次，对于发行期限在一年及一年以上的附息债券，需进行筛选。如果有两只或两只以上的债券具有相同的到期日，仅挑选具有最小买卖价差的那只债券进入样本池。再次，剔除所有发行期限大于一年但剩余期限小于一年的附息债券。最后，遵循Bliss(1996)[24]，剔除含权和特殊流动性问题的个券(13)在本研究样本期间，银行间市场流通的国债中没有含权债券。。

之后，将经过筛选的月度横截面样本分为两个子样本集——样本内子集和样本外子集，各占样本全集大约50%。对于正文中定义的每个期限区间，我们结合买卖价差和成交量进行分组：有成交量数据并且买卖价差较小的债券具有较高的流动性，交易较为活跃，优先选入样本内子集。因此，所有活跃券(包括on-the-run债券)均被分入样本内子集用于估计。

表3展示了样本期所有样本券在不同样本子集以及不同期限子区间的分布情况。大多数期限子区间基本按照其成交量情况分组：有成交量数据的债券优先分入样本内子集，无成交量数据的债券进入样本外子集，因此两个子样本组间可能存在一定差异。期限在一年以下的债券具有较高的流动性，因此更多的被分配在样本内。在分组时，发行期限为一年的附息债券与零息债券具有一定的替代关系，因此其分配情况与零息债券相反，更多的被放在样本外数据组。由表中数据可以看出期限在30～50年的流通券数量较少，为均衡两个子样本组的数据分配，此区间内样本基本按照50%的比例进行分配。

表3 样本债券分组统计

注：样本期为2009年1月至2018年12月，共选取了中国银行间国债市场120个月的月末数据。