以“勾股定理的应用”为例谈初中数学的建模教学
2020-04-20安少敏
安少敏

【摘要】数学教学中离不开学生各种能力的培养与提高,只有当学生的数学能力得到提高时,才能提高学习成绩。数学建模教学就属于培养学生数学能力的一种有效方式,在实际的教学中,需要教师采用高效灵活的教学方式,促使学生获得全面发展。
【關键词】勾股定理 初中 数学 建模教学
【中图分类号】G633.6 【文献标识码】A 【文章编号】2095-3089(2020)04-0133-01
初中阶段的数学教学也较为重要,需要为高中阶段的数学教学打下坚实牢靠的基础。因此在这一时期的教学中,教师就要从培养学生的数学建模意识开始,让学生养成良好的学习习惯,发散学生的思维,提高学生的数形结合能力。
一、创设教学情境
勾股定理教学不仅是初中阶段的数学教学重难点,在学生今后的数学学习中也是重难点之一。教师在实际教学中,就可以以勾股定理为例,来逐渐培养学生的建模意识。这时,就需要对教师的教学方法有很高的要求,教师的教学方法一定要体现出趣味性、实效性、合理性、创新性,这样才能吸引学生注意力,激发学生兴趣,促使学生积极主动参与数学知识的学习。
创设教学情境,相信在如今的课堂教学中,已经不再陌生,而且是一种应用非常广泛的教学模式。教学情境的创设,能够为学生营造真实的学习情境,引发学生的思考,为学生的思维插上想象的翅膀,尽情发挥,尽情畅想,进而收获数学知识。在真实的情境中,还有利于激发学生的真实情感,让学生带着浓烈的情感参与数学学习,认识到数学建模的重要性与作用,在实践、探究、体验中获得提升。
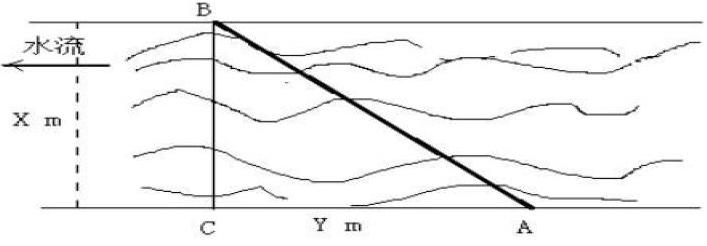
例如:如下图所示,小莉和小明两人在一条河道内放纸船,这段河道的河岸近似为直线,小莉的纸船从河岸A点向对岸飘去,因为河水流动的原因,小莉的纸船达到对岸B点时,小明的纸船已经在A点的下游C点了。已知C点为对岸B点的垂直对应点,假设河道宽为X,AC之间的距离为Y米,求出小莉纸船从A点飘到B点的距离?
解析:已知C点为对岸B点的垂直对应点,可以通过直角三角形的模型构建,利用勾股定理来解答。
二、鼓励学生善于质疑
鼓励学生善于质疑,让学生在一边思考中一边分析,能够发散学生的思维,培养学生的解决问题能力,还能促使学生养成良好的自主学习习惯,及时挖掘问题,并通过解决来获得提升。在实际的教学中,教师需要做好引导工作。要根据实际的课堂教学内容,结合学生的特点,为学生制定针对性的问题,通过新颖、具体的方式呈现在学生面前,引发学生思考,为数学课堂注入更多活力。在学生思考中,教师还要做好引导工作,帮助学生及时解答疑惑,并根据学生的表现进行评价奖励,让学生对数学学习充满浓厚兴趣。
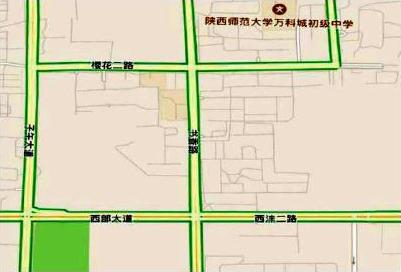
例如:每到旅游期间,就会出现堵车现象。一旦出现比较严重的堵车现象,将会浪费我们很多的时间,还会带来很多困扰。接下来教师可以为学生展示以下路线图:
通过直观形象图形的展示,就快速吸引了学生的注意力和兴趣。这时教师提出问题,如果西部大道和子午大道都堵车时,我们应该怎样做?然后鼓励学生敢于质疑,提出问题。这时,有学生就提出,连接子午大道与西部大道的斜边,将其看作一个三角形,然后从斜边穿过,就会避免堵车。
三、通过多角度解决问题
在数学课堂教学中,师生都扮演着非常重要的角色。然而教师要想对学生有充足的了解,还要积极与学生转换身份,站在学生的角度去思考问题,进而让学生能够从多个角度,去分析问题、思考问题、解决问题,提高自身的知识灵活运用能力。在实际教学中,教师要有意识、有目的、有计划的去引导学生,站在学生的角度去提出问题,然后引导学生从多个角度去看待问题与解决问题,进而提高学生的数学建模能力。
例如:我们学校的操场是一个长方形,已知它的长度为200米,宽度为100米,那么它的斜边是多少米?该怎样去计算呢?
这时学生就会提出,用勾股定理进行模型构建,进而得出斜边。
假设斜边为C,那么有公式C2=2002+1002
接下来教师在提出假设,那如果我们学校的操场如下图所示,如果从A点走到B点,该选择怎样的线路呢?这道题中有直角三角形吗?
当学生回答不存在时,教师再一次提问,那么该怎样解决这道习题?
这时学生回答,可以在其中通过直角三角形的构建,利用勾股定理,进而得出AB之间的距离。
结语:综上所述,在初中数学教学中展开建模教学也非常重要,需要受到教师的高度关注。在今后的数学教学中,教师可以通过创设教学情境、鼓励学生质疑、通过多角度解决问题的方法,来培养学生的数学建模意识,提高学生的建模能力,进而提高学生的学习成绩。
参考文献:
[1]唐成刚.浅谈初中数学的建模教学——以“勾股定理的应用”为例[J].读写算,2018(23):110.
[2]屠静波.以“勾股定理的应用”为例谈初中数学的建模教学[J].中学数学,2017(24):65-66.
