基于Linear Cohesion模型的含水堆积体滑坡过程数值模拟

高道路， 王林峰

(1.重庆交通大学 土木工程学院， 重庆 400074； 2.重庆交通大学 河海学院， 重庆 400074)

1 研究背景

近年来，世界各地发生滑坡等地质灾害的频率越来越高，造成了大量人员伤亡和财产损失[1-3]。滑坡按岩体性质可划分为岩质滑坡、土层滑坡和松散堆积层滑坡3类，其中，松散堆积层滑坡由于岩体结构组成极为复杂，如何准确地计算其运动特征是当前的研究热点和难点[4]。

目前，滑坡灾害的研究主要包括室内试验和数值分析，小规模滑坡可以通过室内试验进行模拟并得到较为可靠的结果，但数值分析法可以不受尺度的限制，能够模拟更加真实尺寸的滑坡运动过程[5-6]。Zhou等[7]采用离散元法中的干颗粒流模型研究了固体颗粒沿斜坡通道的接触行为，确定了颗粒流滑动速度分布和相应的剪切速率。刘思杰等[8]采用三维颗粒离散元对不同粒径的碎屑流运动进行分析，发现粒径组成越不均匀，滑坡运动速度和破坏力越大，滑动距离也越远。Lo等[9]利用离散元程序PFC对某滑坡的运动和土体破坏的运动过程进行了系统分析，发现不同摩擦系数和粘结强度对滑坡堆积范围的影响。Mead等[10]采用数值分析法模拟了在不规则地形上干燥细沙堆积体的运动过程，数值试验结果与室内物理试验结果基本一致，证明了采用数值方法模拟堆积体滑坡是合理可行的。

大量相关文献研究成果表明，采用数值试验分析计算滑坡的运动过程可以得到较为准确的结果，特别是基于非连续介质理论的离散元法应用尤为广泛。总体来说，已有大量学者采用数值分析法模拟各类滑坡体的运动，并取得了丰硕成果，但在滑坡运动模拟过程中直接考虑水的黏附作用的相关研究还很少。

因此，本文在传统离散单元法软球模型的基础上，直接引入颗粒单元间的液桥力，提出采用Linear Cohesion接触模型模拟含水湿润状态下颗粒堆积体的滑动过程，并进一步研究不同液桥力大小对堆积体滑坡各项运动特征的影响。

2 接触模型简介

离散单元法(Discrete element method，以下简称DEM)是Cundall等[11]在20世纪70年代首次提出的描述节理岩体和非连续介质力学行为的有效数值方法。DEM认为节理岩体由离散的块体和块体之间的节理面组成，不仅可以考虑岩体内部结构的大位移、旋转和滑动，甚至还可以计算块体的分离过程，能客观真实地反映裂隙岩体非线性大变形的特点，特别适用于裂隙岩体的应力变形分析[12]。与传统的有限元方法相比，DEM方法提供了丰富的颗粒单元接触模型，可以很好地解决裂隙岩体的大变形问题。

本文主要计算松散堆积体在干燥和含水湿润两种状态下的滑动过程。其中，针对松散堆积体在干燥状态下的失稳、滑动和堆积整个过程，接触模型采用了常用的Hertz-Mindlin滑动模型，如图1所示，为两颗粒单元i和j的接触示意，图1中所示的kn、kt、kr分别为法向刚度、切向刚度和滚动刚度，dn、dt、dr分别为法向阻尼、切向阻尼和滚动阻尼。

图1 Hertz-Mindlin颗粒接触模型

对于模拟含水湿润状态下松散堆积体滑动过程，由于两相互接触的颗粒间形成了液桥，因此，需引入液桥力来模拟。本文采用Linear Cohesion接触模型模拟含水湿润状态下松散堆积体滑动过程，该模型是在传统Hertz-Mindlin软球无滑动接触模型的基础上增加一个法向黏聚力。此时，堆积体颗粒在滑动过程中受3种力的作用，包括重力、颗粒间接触力和液桥力。除此之外，互相接触的颗粒单元还受到切向力矩和滚动摩擦力矩的作用，规定第i个颗粒的运动方程[13-14]如下:

(1)

(2)

式中:m为颗粒的质量，kg；I为颗粒的转动惯量,kg/m2；g为重力加速度,m/s2；ni为与小球i接触的颗粒总数量；V为运动速度,m/s；ω为角速度,rad/s；t为时间,s；Fn,ij和Ft,ij分别为法向和切向作用力,N；Fcoh,ij为两颗粒间的液桥力,N；Tt,ij和Tr,ij分别为切向力矩和滚动摩擦力矩,N·m。Linear Cohesion接触模型模中的液桥力Fcoh定义如下：

Fcoh=kA

(3)

式中:A为两颗粒的接触面积m2;k为颗粒间的粘结能量密度,J/m3。

3 模型建立与计算条件

利用Auto-CAD建立了三维松散堆积滑坡数值试验模型，并将其导入离散元程序EDEM2017中进行计算，建立的滑坡数值模型如图2所示，包括底板、侧板和堆积体物源。底板水平长度为20 m，坡长16.77 m，水槽宽度为1.5 m，滑坡模型的坡角设置为27°(1∶2)，边坡垂直高度为7.5 m，斜槽水平投影长度为15 m，松散堆积物由1 470个颗粒组成，颗粒形状参照实际岩屑进行建模，如图3所示。堆积体物源总质量为5 687 kg，堆积物总体积约为3.2 m3。

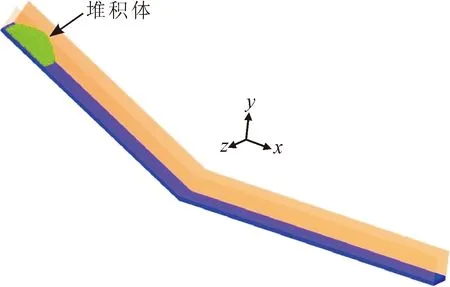
图2 堆积体滑坡数值模型

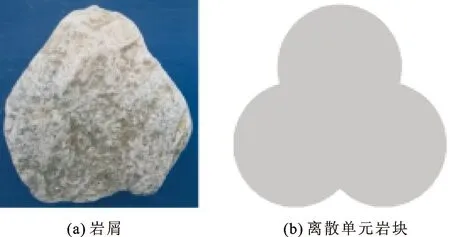
图3 松散堆积体的颗粒单元

此外，采用Linear cohesion模型模拟含水松散堆积体滑坡运动时，需要输入相应的能量密度k，由于缺乏相关的资料作为参考，本文通过反复迭代试算，并讨论不同能量密度取值对含水松散堆积体滑坡运动特性的影响，最终采用的能量密度从1 000 J/m3开始递增至6 000 J/m3。其余计算参数还包含颗粒密度、泊松比和摩擦系数等，参考了类似的颗粒离散元数值试验并进行优化[15]，详细参数取值见表1。

4 结果与分析

在本次松散堆积体滑坡数值试验中，计算研究了干燥颗粒和含水湿润颗粒的运动过程和堆积特点，包含能量密度k取0(干燥状态)、1 000、2 000、3 000、4 000、5 000和6 000 J/m3等7种计算条件，运动过程中不同时刻的滑动速度如图4～8所示，由于图幅较多，仅给出部分结果。

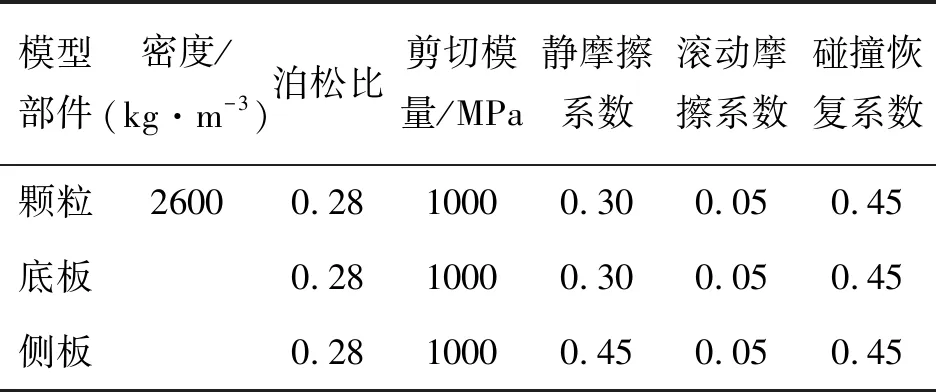
表1 离散元模型相关参数

分析可知，当能量密度k取0时，即原堆积体是干燥的，此时松散颗粒堆积体滑动时具有良好的流动性，滑槽上颗粒的速度在滑动过程中不断变化。在t=3.1 s时，前颗粒到达水平面，最大速度超过7 m/s，最终当t=8 s时运动基本停止，颗粒流堆积在斜槽和平面上，运动的距离较长(图4)。此外，为了分析能量密度k对松散堆积体滑坡运动的影响，计算了松散湿颗粒在考虑能量密度的情况下的滑动过程(图5～8)。分析可知，随着能量密度k的逐渐增大，颗粒堆积体滑动时的流动性越来越小，如图6(k=2 000 J/m3)所示，堆积体在斜坡上运动时前段解体为小颗粒群运动，而后段滑动时基本保持结构完整，最终当t=8 s时运动基本停止，但此时堆积体主要堆积在平面上，极少数颗粒堆积在斜坡上。能量密度越大，堆积体滑动到坡脚位置所消耗的时间也越长，如k取0，为3.1 s，而取1 000和2 000 J/m3时延迟到3.4和3.7 s。

当能量密度k超过4 000 J/m3时，松散湿颗粒堆积体在斜槽上滑动时(t=0～4 s)均能保持初始状态的结构完整，这是由于足够的能量密度k赋予了颗粒间较大的液桥力，可以抵消外界一定强度的作用力，当所受力不超过液桥力时，颗粒粘结结构依旧能保持完整。如图7中当k=4 000 J/m3时，仅当松散堆积体冲撞到底部平面时，由于惯性作用，前端颗粒速度远大于后端颗粒，堆积体前端开始出现拉裂隙，最前端的颗粒逐渐团脱离母体运动。而图8中当k=6 000 J/m3时，整个堆积体滑动过程中结构一直保持初始的状态，即便在水平面上运动时颗粒粘结依旧未被破坏。

以上分析表明，较小的能量密度可以使松散湿颗粒堆积物在滑动过程中发生崩解，形成数个破碎的岩屑颗粒群单独运动，并形成较远的滑动距离。

图9给出了不同能量密度参数时松散堆积体整体平均运动速度和动能随时间的变化情况。

图9表明，随着堆积体颗粒间的能量密度逐渐增大，滑动达到最大平均速度和动能峰值的时刻越来越早，数值越来越大，但是当k≥5 000 J/m3时，堆积体滑动的各项运动特征差别非常小。

图4 不同时刻干燥堆积体滑动速度分布(k=0)

图5 不同时刻含水堆积体滑动速度分布(k=1 000 J/m3)

图6 不同时刻含水堆积体滑动速度分布(k=2 000 J/m3)

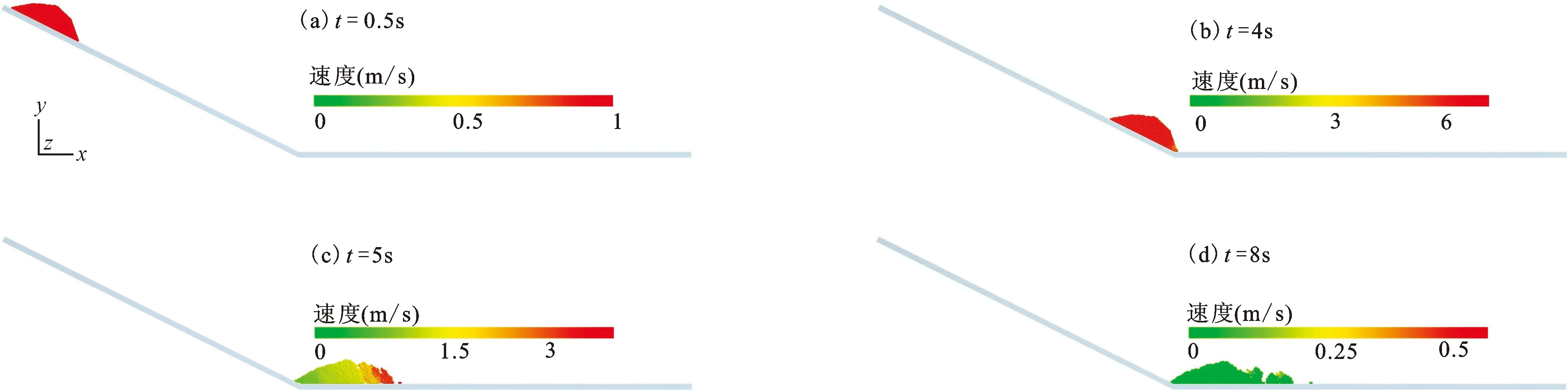
图7 不同时刻含水堆积体滑动速度分布(k=4 000 J/m3)

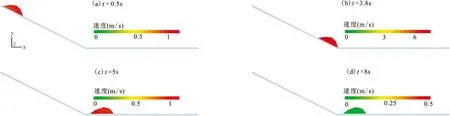
图8 不同时刻含水堆积体滑动速度分布(k=6 000 J/m3)

例如，当k取5 000和6 000 J/m3时，堆积体运动的最大速度分别为6.69和6.71 m/s，最大动能分别为127和128 kJ，差别很小，对应的时刻均在t=3.8 s。而当k取2 000 J/m3时，堆积体运动的最大速度和最大动能分别为4.65 m/s和63.5 kJ，对应的时刻为t=4.4 s。

进一步分析发现，当k≥4 000 J/m3时，堆积体滑动速度曲线峰值前段几乎呈线性增加，这是由于此时的堆积体结构在坡面保持整体运动。动能曲线图9(b)与9(a)中的速度曲线趋势基本一致，因为速度与动能之间的关系为Ek=1/2(mv2)。此外，当k不超过3 000 J/m3时，松散堆积体取不同能量密度时滑动最大速度和最大动能差异不大。

图10为不同能量密度松散堆积体x、y、z方向的滑动速度。在x方向(图10(a))，沿滑动运动方向，变化趋势与图9(a)中体积速度的变化趋势非常相似，同样，能量密度越大，堆积体达到x方向的最大平均速度越早，最大平均速度越大。在y方向(图10(b))，速度负值表示垂直向下的滑动运动，当能量密度k<3 000 J/m3时，堆积体y方向的最大平均速度差别不大，约在1.8 m/s左右，而当k≥5 000 J/m3时，y方向的最大平均速度几乎可以达到3 m/s。此外，在z方向，该速度代表湿颗粒沉积物的横向运动，所有情况下z方向的最大平均速度约为2～3 cm/s，集中在4～6 s，由于侧板的阻挡作用，其大小比x和y方向小两个数量级，如图10(c)所示。

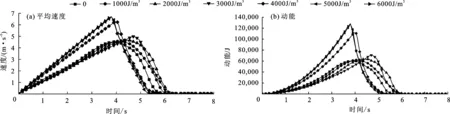
图9 不同k值松散堆积体滑动平均速度和动能变化

图10 不同k值松散堆积体滑坡x、y、z方向平均速度变化

表2给出了松散堆积体滑动后的堆积长度统计结果，结合图4～8可知，随着堆积体能量密度的逐渐增加，斜坡上和平面上的堆积长度均有逐渐减小的趋势，如k=1 000 J/m3时，斜坡上的堆积长度和平面上的堆积长度分别为4.72和7.59 m，当能量密度增加到3 000 J/m3，堆积长度分别减小到0.96和4.73 m，当能量密度增加到5 000 J/m3，堆积长度进一步减小到0和5.30 m。以上分析说明，能量密度较小的情况下，湿颗粒堆积体流动性更强，在实际滑坡运动过程中，滑坡灾害的影响范围更广。

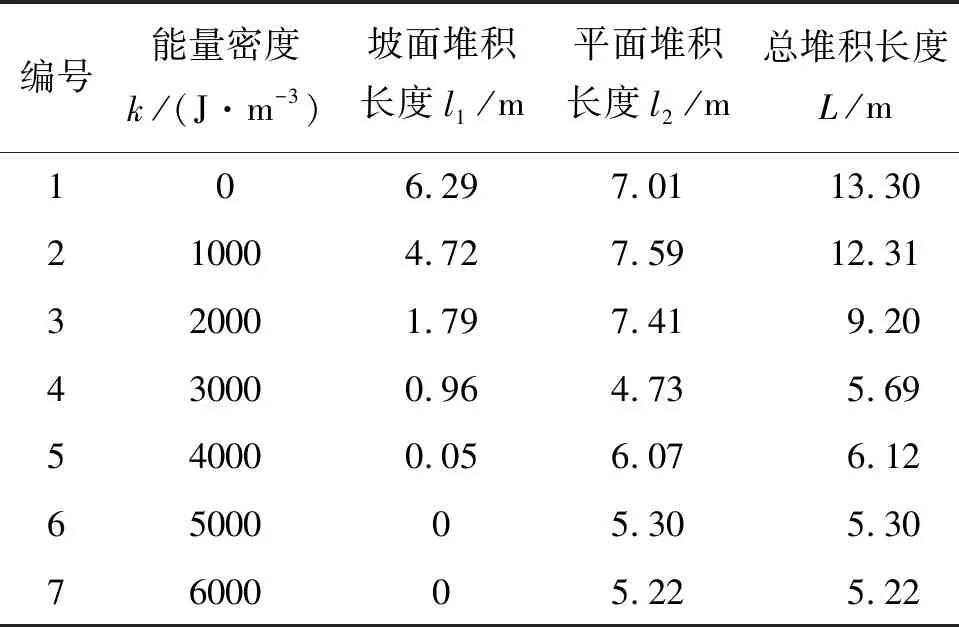
表2 含水堆积体滑坡滑动方向堆积长度

图11为不同能量密度堆积体滑动过程中颗粒接触数量的变化情况。结果表明，当能量密度不超过3 000 J/m3时，颗粒的接触数量在第1阶段(t=0～4 s)逐渐减少，然后逐渐增加，最后趋于稳定并保持不变。而当能量密度k≥4 000 J/m3时，颗粒的接触数量在第1阶段(t=0～4 s)保持不变，在t=4 s时出现陡然增加，这是由于堆积体刚好撞击到底部平板上，然后接触数量逐渐减小，最后趋于稳定并保持不变。

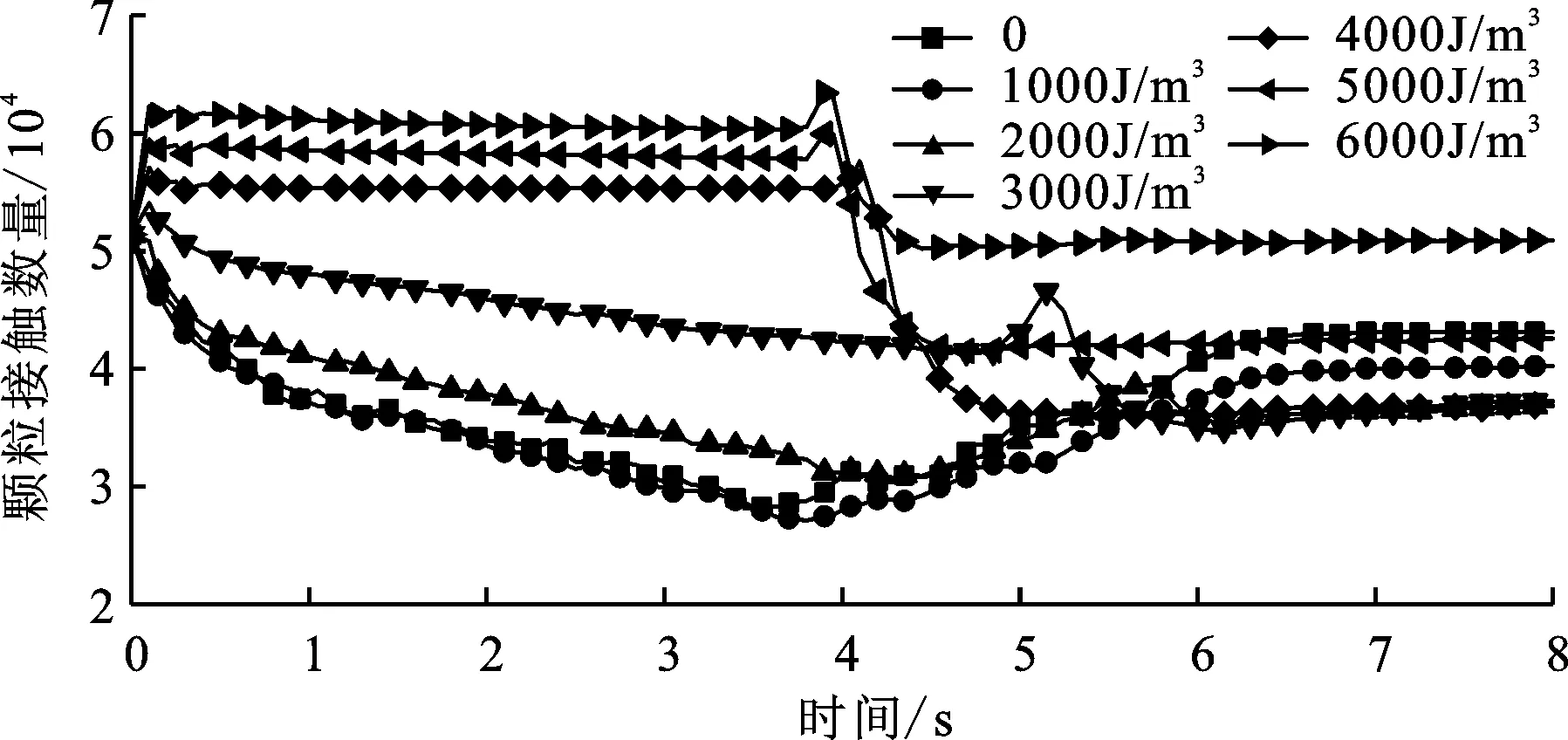
图11 松散堆积体滑动过程颗粒接触数量变化

5 结 论

本文在传统离散单元法软球模型的基础上，提出了一种采用Linear Cohesion接触模型模拟含水湿润状态下的松散堆积体滑坡运动过程的分析方法，该模拟可以有效地考虑相互接触颗粒单元之间的液桥力，并引入了能量密度参数k进行表征。通过建立含水堆积体滑坡离散元数值试验模型，研究了不同能量密度值对堆积体滑坡各项运动特征的影响，得到以下结论：

(1)随着堆积体颗粒间能量密度逐渐增大，堆积体滑动时的流动性越来越小，堆积体滑动到坡脚位置所消耗的时间也越长，达到最大平均速度和动能峰值的时刻越来越早，数值越来越大。当k≥5 000 J/m3时，堆积体滑动的各项运动特征差别非常小。

(2)较小能量密度的松散湿颗粒堆积物在滑动过程中极易发生崩解，形成的岩屑颗粒群单独运动，流动性更强，在斜坡和平面上的堆积长度更长，此类滑坡灾害的影响范围更广。

(3)能量密度对含水堆积体滑坡过程中颗粒的碰撞接触影响较大，当能量密度k≤3 000 J/m3时，颗粒的接触数量先减少然后增加，最后趋于稳定；当能量密度k≥4 000 J/m3时，接触数量先保持不变，之后陡然增加，最终趋于稳定。

以上结论表明Linear Cohesion接触模型可以较好地反映含水湿颗粒间的相互作用，可用于模拟含水松散堆积体滑坡的整个运动过程，为今后此类滑坡灾害的数值分析预测和灾害评估提供一种新的研究途径。能量密度k是Linear Cohesion接触模型模拟含水堆积体颗粒运动的关键参数，在今后的研究中有必要对堆积体的含水量与胶结能量密度的关系进行更深入的探讨，进而可以根据不同含水条件选取相应的能量密度值进行含水松散堆积体滑坡的数值模拟计算。