输电杆塔攀爬机器人运动学分析与仿真

耿亚丽，韦佳钰 ，付 渊，鲁守银

（1.山东建筑大学，山东 济南 250101；2.贵阳供电局，贵州 贵阳 550000）

0 引言

我国输电杆塔数量多、分布广，杆塔长期暴露于野外受到风吹日晒、粉尘等影响会存在安全隐患，甚至会发生安全事故，因此需要对其进行周期性的巡检与维护。传统方式下，架空输电线路的维护需电力人员登塔至高处进行作业，安全防坠装置是必不可少的防护工具，但首位登塔挂接及末位拆除安全防坠装置的人员均无法得到安全绳防坠保护。输电杆塔表面结构复杂且不规则，如螺栓固定区、连接处的节点板、脚钉角钢叠加区等区域给攀爬工作带来许多障碍，如图1 所示。随着机器人技术的发展，多种电力特种机器人已经能够代替人工完成包括输电线巡检、带电作业等部分输电线路工作任务［1］，采用机器人进行输电杆塔攀爬以完成安全防坠装置的挂拆及携带电力巡检设备等任务已具备一定条件［2］。输电杆塔攀爬机器人不仅可以承受恶劣的工作环境，降低高空攀爬的危险系数，多机联合工作更是可以大幅提升巡检维护作业的效率，缩短巡检时 长［3］。

图1 输电杆塔结构

20 世纪80 年代，美国、日本等发达国家先后开展了攀爬机器人研究工作。东京工业大学研制了一款NINJA 四足机器人，该机器人运用阀控式多油抽杆，可以吸附在墙面上［4］。MIT 团队设计了一款攀爬桁架结构的机器人，该机器人通过中间的一根连杆连接了两端的夹持爪，尺寸较小［5］。英国威尔士班戈大学设计了一种电磁吸附式的攀爬机器人，可用于攀爬输电杆塔，该机器人由3 部分组成，每部分安装有电磁吸附装置［6］。以色列艾瑞尔中心大学设计了一款电磁吸附式爬铁塔机器人［7］，采用了八自由度连杆式结构，能够蠕动式在桁架攀爬。

相较于国外，国内对于攀爬机器人的研究起步较晚。自2000 年以来，国内一批大学和科研院所等陆续开展了攀爬机器人研究工作，并取得一定的研究成果［8］。哈尔滨工业大学李勇兵等依据昆虫运动原理设计了一种对称结构的双足机器人构型攀爬机器人［9］，该机器人主要采用铝合金材料加工而成，整体质量较轻。四川大学的陆小龙、赵世平等设计了一种攀爬机器人夹持机构［10］，针对角钢特有的结构，该夹持机构能够较好地完成角钢的夹持动作，夹持住杆塔角钢主材，两个夹持机构通过异步开合来配合丝杠螺母动作从而实现沿杆塔的攀爬，并在实验室理想情况下进行了实验。后来四川大学又对该机构进行了改进［11］，利用电动推杆控制攀爬机构的张合，可以实现与机器人在同一水平面上高度或长度较小障碍物的跨越。南京工程学院在三维模型下设计了一种用于攀爬输电杆塔的机器人，基于概念设计机器人适应能力较强，具有一定的夹持力。

输电杆塔攀爬机器人是通信、机械、电子、计算机以及自动化等众多学科融合交叉的产物，目前国内外尚未有成熟的产品，所产样机也是在实验室理想情况下完成。因此，研制一款适用于现场实物杆塔能够攀爬完成相应指定任务的机器人，对于电力行业具有重要意义。

针对实现输电杆塔的攀爬以及杆塔上障碍物的跨越，同时完成挂拆安全防坠装置操作的要求，依据仿生学原理设计了一种九自由度的攀爬机器人攀爬机构和六自由度的挂拆机械臂，为了验证设计攀爬机器人的可行性，运用D-H 表示法对其建模，并进行正运动学分析，列出本体和机械臂各个关节在给定参考坐标系下的运动学方程，通过使用MATLAB 仿真软件对本体和机械臂进行运动仿真。

1 攀爬机器人机械结构设计

输电杆塔攀爬机器人需要在输电杆塔复杂的桁架结构上运行，合理可靠的机械设计是进行输电杆塔攀爬完成挂拆作业任务的基础。设计的输电杆塔攀爬机器人机械结构主要由攀爬机器人攀爬机构和挂拆机械臂两大部分组成。依据仿生学原理进行分析，模仿了猿类在爬树时的姿势及动作序列，设计了九自由度的攀爬机构，上下夹持爪各有4 个自由度，上夹持爪模仿的是猿类爬树时上肢各关节的姿势及动作序列，下夹持爪模仿的是猿类爬树时下肢各关节的姿势及动作序列。挂拆机械臂模仿人类手臂关节结构设计。输电杆塔攀爬机器人机械结构如图2 所示。攀爬机器人本体主要包括上夹持爪、升降机构、下夹持爪，攀爬机器人本体主要用于完成沿输电杆塔主材侧的攀爬以及脚钉、角钢等障碍物的跨越。挂拆机械臂主要用于完成安全防坠装置的挂拆，从而保证作业人员的人身安全。

攀爬机器人本体上（下）夹持爪机械结构设计如图3 所示，主要由外展机构、夹持机构、顶出机构组成。上下2 个夹持爪对称布置，设计原理及结构相同。外展机构通过控制电机的正转与反转控制外展距离，外展机构向外展出时可以避开输电杆塔主材、辅材、角钢脚钉等障碍物，外展机构向内收缩时可以环抱主材，配合夹持机构夹持杆塔主材。夹持机构通过控制电机的正转与反转实现抓紧与松开角钢动作。顶出机构主要包含了金属万向头、丝杠、顶出电机，顶出电机通过丝杆与金属万向头连接，控制顶出电机的正反转实现金属万向头的顶进和后退动作，从而配合外展机构避开杆塔主材上众多连接件、脚钉等障碍物，此外当金属万向头行进到最大顶进行程时与杆塔主材折弯（棱）处接触，与夹持机构共同构成着力点，从而保证机器人整体运行的稳定性。

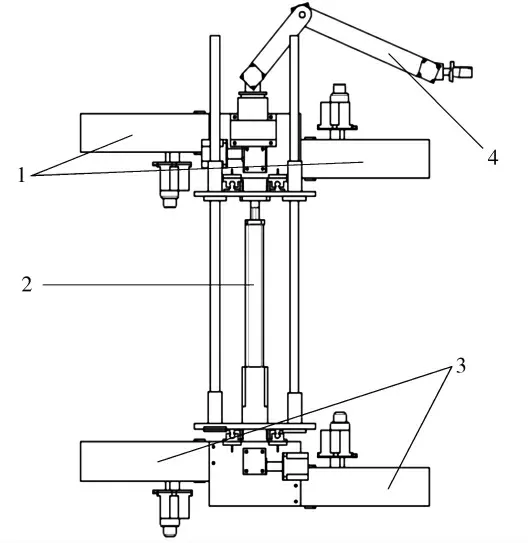
图2 输电杆塔攀爬机器人机械结构

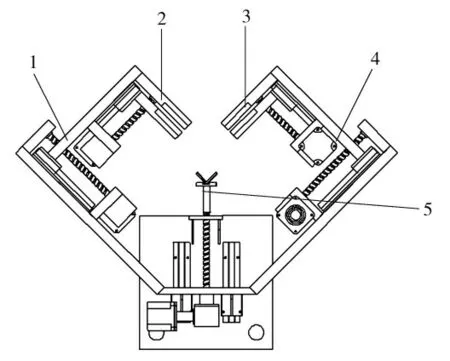
图3 攀爬机器人上（下）夹持爪机械结构

2 攀爬机器人本体运动学分析

所设计攀爬机器人的夹持机构和外展机构各有4 个，本体上部分2 个，下部分2 个，上下部分为对称布置。上下两部分中的夹持机构和外展机构也均为对称布置，通过调整2 个夹持手之间的距离和外展机构的展出距离实现沿杆塔的攀爬。本体共有9 个自由度，建立相应的攀爬机器人本体参考坐标系如图4 所示。

图4 输电杆塔攀爬机器人本体参考坐标系

在建立机械臂D-H 模型时，通过相邻坐标系之间的矩阵变换式得到与其相邻的活动关节坐标变换矩阵，例如坐标系xn-zn变换到下一个坐标系xn+1-zn+1，其变换矩阵为

整理后为

为简化书写，令上式中Sθn+1=sinθn+1，Cθn+1=cosθn+1，Sαn+1=sinαn+1，Cαn+1=cosαn+1。则可得总的变换矩阵为

式中：nx、ny、nz分别为机械臂法向量n 在x、y、z 轴上的投影；Ox、Oy、Oz分别为机械臂移动向量O 在x、y、z轴上的投影；ax、ay、az分别为机械壁接近向量a 在x、y、z 轴上的投影；px、py、pz分别为机械臂在x、y、z 轴上的位置坐标。

机身上下两部分设计原理相同，同时上（下）部分又可分为左右两部分，左右两部分为对称设计，每一部分包含伸展机构和夹持机构，因此机器人本体在列写变换矩阵时只需要列写升降机构、一部分中的伸展机构和夹持机构3 个位置变换矩阵即可。

升降机构末端与参考坐标系之间的变换为

外展机构末端与参考坐标系之间的变换为

夹持机构末端与参考坐标系之间的变换为：

为了进一步研究和分析机器人本体各部位的运动轨迹，使用MATLAB（2017b）Robotics Toolbox for MATLAB 仿真软件对机械臂进行运动仿真，使用Robotics Toolbox 中Link 功能函数和fkine 正向运动学仿真函数构建输电杆塔攀爬机器人本体升降机构、外展机构、夹持机构仿真模型，分别如图5 所示，根据图像可以分析出各关节的运动方向。

图5 机构仿真

3 挂拆机械臂运动学分析

3.1 挂拆机械臂模型

根据挂拆要求设计了六自由度的机械臂，该挂拆机械臂是参考人体手臂结构设计，采用的结构是开链式关节型，主要分为基关节、肩关节、大臂、肘关节、小臂、腕关节等结构，该机械臂的各个关节均为旋转关节。六自由度挂拆机械臂模型如图6 所示。

图6 六自由度挂拆机械臂模型

3.2 机械臂运动学分析

在机械臂末端执行器根据不同要求动作时，首先要确定机械臂整体在空间的位置和姿态，因此在机械臂上固连一个基坐标，然后通过描述该坐标系的原点在固定坐标系位置以及该坐标系相对于固定坐标系姿态，可以描述执行器在固定坐标系的位置和姿态［12-13］。在机器臂执行任务时需要考虑以下2个问题：1）已知机器人关节角变量，计算机器人末端相对于基坐标位置和姿态；2）给定机器人末端执行器的位置和姿态，计算机器人的各个关节角度［14］。

为了描述挂拆机械臂基座和手爪之间各个结构在空间的位置和姿态，采用D-H 表示法（四参数法）建立参考坐标系及各个关节的坐标系从而推到挂拆机械臂的运动方程［15-16］。

D-H 表示法是由Denavit 和Hartenberg 于1995年提出的一种建立相对位置和姿态的矩阵方法［13］。由ax、αx、dx、θx4 个参数描述机械臂各个关节与相邻坐标系之间的关系，从而推导出机械臂末端执行器的坐标系相对于基坐标的等价齐次坐标变换矩阵，建立相应的运动方程［17-18］。为计算方便，选取特定六自由度挂拆机械臂的位姿及参考坐标系，六自由度挂拆机械臂参考坐标系如图7 所示。根据图7 得到机械臂D-H 参数，如表1 所示。

将参数表中的4 个相关参数代入矩阵An+1，得到相应关节的矩阵A1、A2、A3、A4、A5、A6。

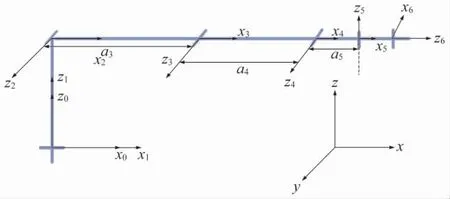
图7 六自由度挂拆机械臂参考坐标系

表1 机械臂D-H 参数

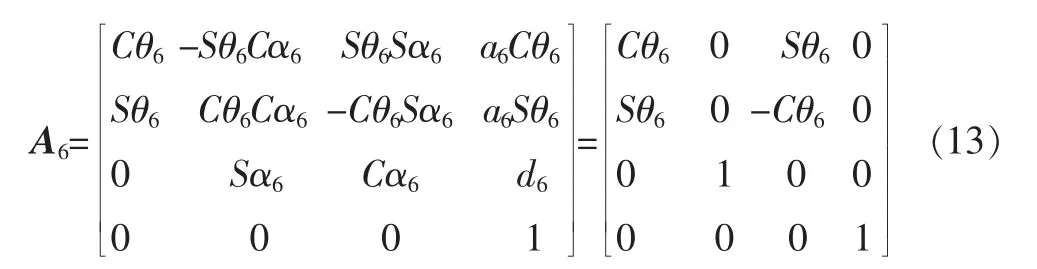
机械臂基座与手抓之间的总变换公式经计算如式（14）所示，其中Ci＝Cθi，Cij＝C（θi+θj），Cijk=C（θi+θj+θk），Si=Sθi，Sij=S（θi+θj），Sijk=S（θi+θj+θk）。

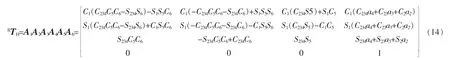
综上所述，式（14）为六自由度挂拆机械臂选定位姿正运动学模型的一般表达式。

3.3 机械臂运动学仿真

为了进一步研究和分析挂拆机械臂的运动轨迹，使用MATLA（2017b）Robotics Toolbox for MATLAB仿真软件对机械臂进行运动仿真，使用Robotics Toolbox中Link功能函数和fkine正向运动学仿真函数构建挂拆机械臂仿真模型。相应的程序如下。

运行程序后输出结果显示如表2所示。

根据多次测试当整个运动发生在2 s内时，采样周期选取50 ms挂拆机械臂响应速度较快，得到的活动关节的位移、速度、加速度变化曲线最为平缓，挂拆机械臂的初始位置和姿态如图8所示。在选取的响应时间和采样周期内，挂拆机械臂各个活动关节运动到采样周期结束时终止位置和姿态如图9所示。

表2 关节参数

图8 挂拆机械臂的初始位置和姿态

图9 挂拆机械臂的终止位置和姿态

挂拆机械臂6 个活动关节的位移、速度、加速度变化曲线如图10 所示。从图10 可知，在整个运动发生在2 s 内，采样周期选取50 ms 时，挂拆机械臂在运动过程中的位移变化、速度变化、加速度变化曲线平滑且持续稳定，说明机械臂实现了由关节空间关节量变化到末端执行器在笛卡尔空间进行起始点到目标点之间运动的转化；速度、加速度的初值和末端值均为零，进一步证明了挂拆机械臂在工作空间内运动的可行性。

图10 挂拆机械臂位移、速度、加速度变化曲线

4 试验

依据电力系统安全工作规定及电力杆塔高空作业安全防护要求，在山东建筑大学智能技术与机器人系统研究院进行了输电杆塔模拟环境主材攀爬测试以及户外输电杆塔仿真环境测试，验证了攀爬机器人高空作业的可行性。在攀爬杆塔、挂拆安全防坠装置的过程中，各关节功能正常，作业灵活，无摩擦碰撞，夹持爪的夹持力足以克服自身重力，未出现整机下滑和坠落现象，满足安全作业要求。攀爬试验如图11 所示。

5 结语

图11 攀爬试验

针对输电杆塔攀爬机器人攀爬输电杆塔和挂拆安全防坠装置的要求设计了九自由度攀爬机器人本体和六自由度挂拆机械臂模型，运用D-H 表示法对本体和机械臂进行了建模与正运动学分析，运用MATLAB（2017b）Robotics Toolbox for MATLAB 仿真软件对本体和机械臂进行轨迹规划和运动仿真，同时进行了现场试验，验证了其可行性，为今后进行其他相关领域的研究打下理论基础。