自旋前伸空化回转体高速斜入水稳定性仿真研究

张代国，潘菲菲，张晓乐，3

（1.海装武汉局驻郑州地区军事代表室，河南 郑州 450015；2.郑州机电工程研究所，河南 郑州 450015；3.河南省水下智能装备重点实验室，河南 郑州 450015）

0 引言

鱼雷投放、深水炸弹投放、反潜导弹投放、破障炮弹打击水下目标、飞机水上迫降以及宇宙飞船的回收[1]等过程都涉及到结构入水问题。由于结构入水跨越空气介质和水介质，介质环境发生了较大变化，结构入水后的弹道性能成为该项研究的一个重要方向。入水冲击问题常见于工程流体力学研究，早期结构入水的水弹道研究是从不自旋的鱼雷弹道开始的[2-3]。潘光等[4]对鱼雷入水的载荷进行了研究，给出了鱼雷入水过程受力的动力学方程组，分析了入水冲击压力载荷峰值。魏照宇[5]等分析了回转体高速垂直入水的冲击特性及初期的弹道特性、轨迹与入水超空泡。A·May[6]对弹体入水特点和实验结果进行了总结。矶部孝[7]研究了常规兵器水下弹道的运动规律并开展了大量的实验，对弹丸入水跳弹的现象作了深入的分析并对弹丸的稳定机理作了简要分析。方城林等[8]利用动网格技术，对5种不同头型的轴对称高速射弹垂直入水过程进行了数值模拟，得到了射弹头部线型，与入水速度衰减和入水阻力系数峰值的变化关系。顾建农等[9]研究了球形与普通手枪2种弹丸倾斜入水的轨迹，发现高速旋转普通制式弹丸的入水弹道不稳定，容易发生失稳翻转。张伟等[10]通过实验发现截卵形弹体往往由于受力不均衡在入水后期发生偏转，卵形弹体则在入水前期即发生偏转。通过大量试验研究发现，结构入水问题非常复杂，除了水面跳弹外，入水结构的水弹道容易发散或失稳。

本文采取了刚体 Lagrange结构网格和 Euler流场网格（L/E）耦合的数值仿真方法，对高速自旋回转体由空气高速斜入水进行模拟仿真，研究尖头回转体入水的弹道特性。并探索通过对入水回转体头型进行改进优化，改善结构入水弹道性能的途径。

1 前伸空化回转体构型

常规炮射高速弹丸主要运行在空气介质中，其流体动力头型主要设计为空气动力头型。当弹丸需要由空气中发射入水，由于介质性质发生了变化，原空气动力头型已经不能很好适用于弹丸入水过程。小型弹丸对于入水弹道的偏转不十分敏感，但直径较大的常规尖头弹丸在入水跨介质过程容易发生水下弹道偏斜和发散[7]。本文设计了一种跨气-液介质分段弹丸，该种弹丸头部空化杆伸出，如图1。入水时先由空化杆产生空泡，使得主弹体在入水过程中获得较小的气液界面冲击面，获得比较好的入水特性。

图1 前伸空化回转体构型Fig.1 Configuration of the self-spin forward-extended cavitating body

2 控制方程及计算方法

2.1 控制方程

流体运动采用Euler方法模拟，建立流体欧拉域。控制方程包括质量、动量和能量守恒。

质量守恒：

动量守恒：

能量守恒：

式中：ρ为材料密度；ui为速度分量；p为压力；e为比内能；sij为粘性偏应力张量，sij=

通过封闭容积分析并利用单点高斯积分，可得离散单元物理量（质量、动量及能量）的线性函数的离散方程。

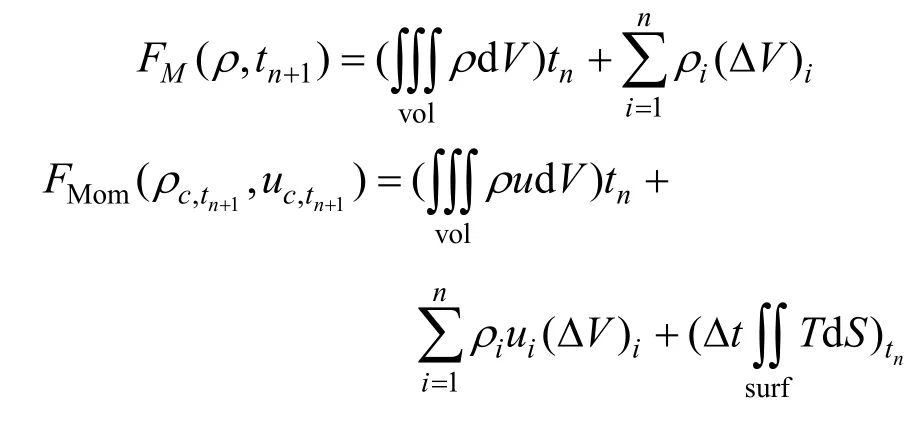
解出单元形心处的各个物理量，可以根据材料本构关系及状态方程，进一步计算出压力等关系。

2.2 耦合算法

本计算中包括固体域和流体域2个计算域。固体域主要模拟回转体，采用 Lagrange方法设置为刚体网格模拟。流体域包括海水和空气所填充的Euler网格区域，采用Euler方法模拟。2个计算域相互重叠，Lagrange网格结构外部定义一封闭耦合面，用于传递2种计算域之间的作用力。对结构冲击动力分析的每一时间步都判断结构域流体间的接触状态，随着冲击的进行，接触面的边界在发生着变化，整个入水过程包含材料非线性、几何非线性和接触非线性等一系列强非线性迭代。

3 计算模型

3.1 回转体及流场模型

回转体模型包括尖头回转体和前伸空化回转体2种。回转体均建立全三维模型，采用Lagrange网格离散，并设置为刚体。为描述三维弹道，回转体6个自由度不固定。尖头回转体头部采用常见的尖头配圆柱回转体结构，如图2所示。前伸空化回转体结构包括前端的空化杆、双曲线头型和后圆柱段，如图3所示。2种回转体轴线均在X-Z平面内，入水角度为坐标系X负向偏Z负向45°，入水速度按400 m/s计，回转体入水前绕回转轴线自旋，自旋速度为6 500 r/min。

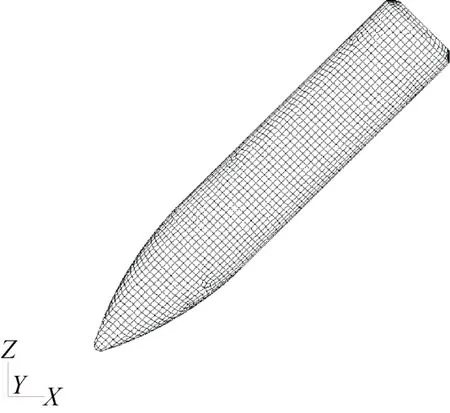
图2 尖头回转体模型Fig.2 Model of the pointed-head self-spin body

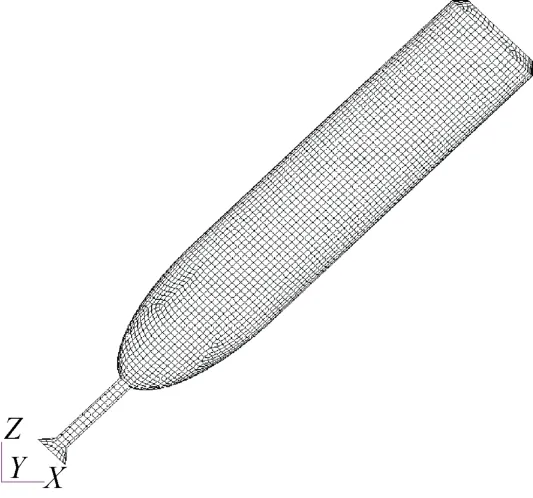
图3 前伸空化回转体模型Fig.3 Model of the self-spin forward-extended cavitating body

3.2 流场模型

流场区域尺寸5 m×2 m×5 m。其中上部1 m深为1个大气压的空气介质，下部4 m深为水介质。流场区域边界均为压力边界，水介质压力边界随水深进行压力赋值。回转体初始位置在空气中，头部45°斜向下接近水面，回转体有4 m×2 m×4 m的水中初始弹道模拟区域。计算区域及边界条件如图 4所示。为保证计算精度，在回转体运行轨迹区域进行网格加密，见图5。

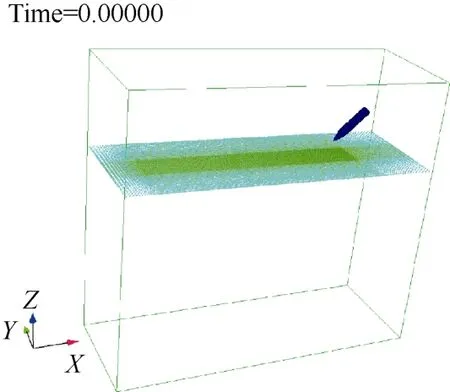
图4 计算域及边界条件Fig.4 Computational domain and boundary conditions

图5 流场计算网格Fig.5 The mesh of fluid flow computation

4 仿真结果与分析

4.1 尖头回转体斜入水初始弹道及姿态

图6给出了尖头回转体头部初始入水后空化开启的状态图。从弹道模拟可以看出，入水一定距离后，回转体质心弹道开始发生明显的偏转，如图7所示。除了质心轨迹偏转外，回转体攻角变化更为显著。入水后攻角一直增大，运行中程攻角增大到了90°，姿态失稳严重，如图8所示。

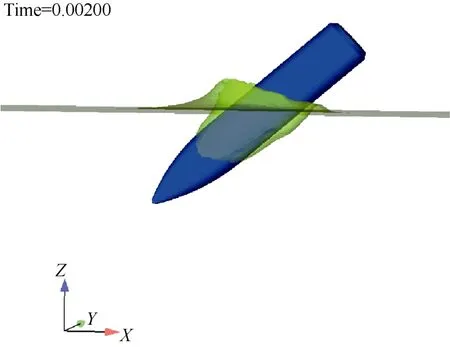
图6 尖头回转体初始入水侧视状态Fig.6 Side view of initial water entry of pointed-head self-spin body

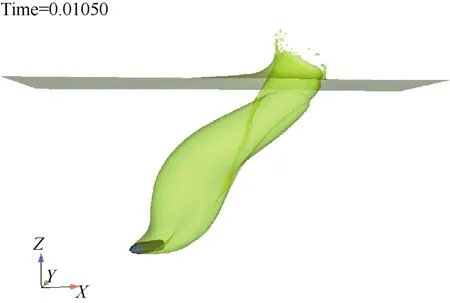
图7 尖头回转体入水过程中侧视状态Fig.7 Side view of pointed-head self-spin body in the course of water entry

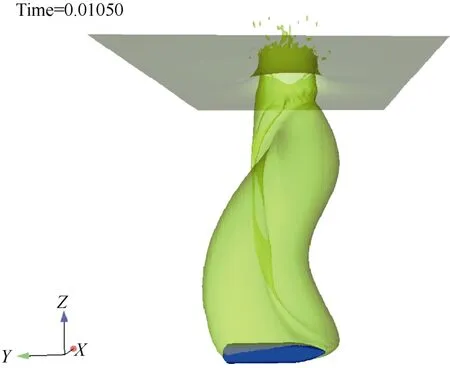
图8 尖头回转体入水过程中前视状态Fig.8 Front view of pointed-head self-spin body in the course of water entry

4.2 流场网格密度影响分析

为了评估网格密度对计算结果的影响，将回转体弹道区域流场网格加密30%。对比加密模型与原网格模型，X向质心位移变化小于0.29%，攻角变化小于1.5%，说明网格密度对计算结果影响较小，如图9和图10。

图9 尖头回转体网格加密前后质心X向位移变化Fig.9 Centroid displacement in X-direction of pointed-head self-spin body before and after increasing the dense of mesh

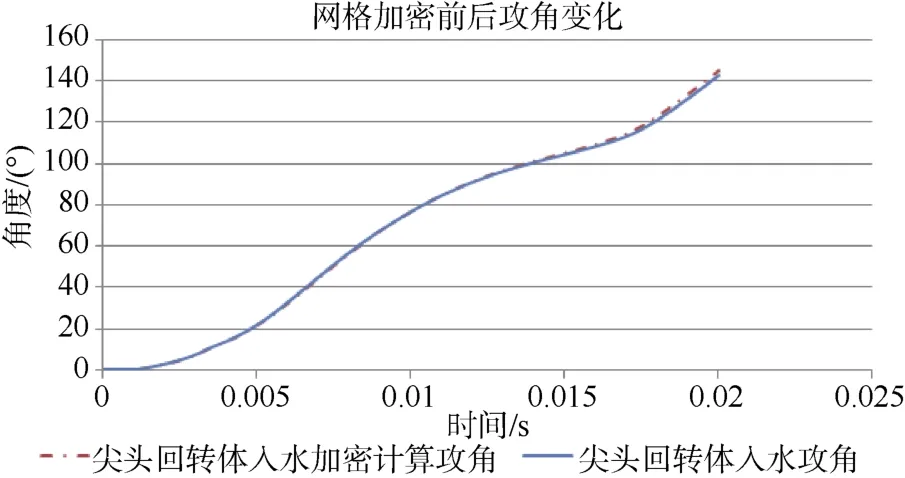
图10 尖头回转体网格加密前后攻角变化Fig.10 Conversion of attack angle of pointed-head self-spin body before and after increasing the dense of mesh

4.3 前伸空化回转体斜入水初始水弹道及姿态

通过尖头回转体入水数值模拟可知，入水后回转体弹道将发生偏转，姿态也有较大变化。为使入水弹道可控，主要对回转体头型进行优化改进。主要包括2点：1）将原回转体尖头变为椭圆曲线头型；2）在椭圆曲线头型上伸出固定的空化杆。图11给出了尖头回转体头部初始入水后空化开启的状态图，可以看出，空化杆在椭圆头型完全入水前已经产生了较为饱满的空泡。

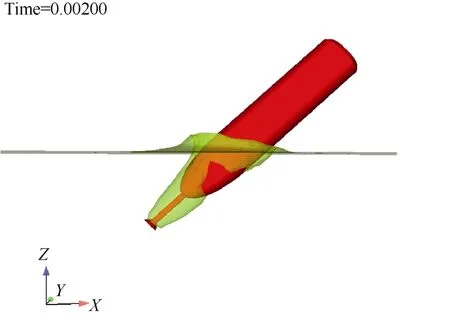
图11 前伸空化回转体初始入水侧视状态Fig.11 Side view of initial water entry of self-spin forward-extended cavitating body

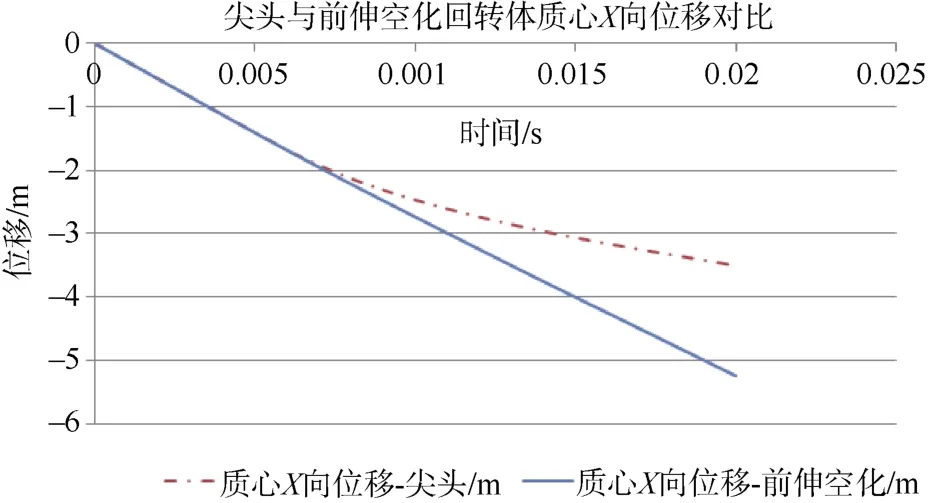
图12 尖头与前伸空化回转体质心X向位移对比Fig.12 Comparison of centroid displacement in X-direction between pointed-head self-spin body and self-spin forward-extended cavitating body

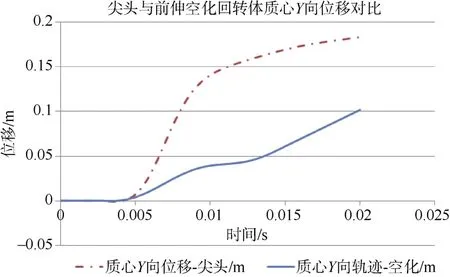
图13 尖头与前伸空化回转体质心Y向位移对比Fig.13 Comparison of centroid displacement in Y-dirction between pointed-head self-spin body and self-spin forward-extended cavitating body

进一步仿真模拟得出了前伸空化回转体入水后质心初始弹道和入水后攻角的变化，尖头与前伸空化回转体3个坐标弹道轨迹对比见图12、图13和图14，攻角变化对比见图15。从弹道模拟可以看出，前伸空化回转体入水后相对于尖头各个方向速度衰减较小，到离开计算域前，其轨迹基本为直线，见图16和图17。前伸空化回转体攻角有轻微变化，且随时间变化攻角趋于稳定。头型改进后，回转体入水弹道稳定性得到了很好的改善。

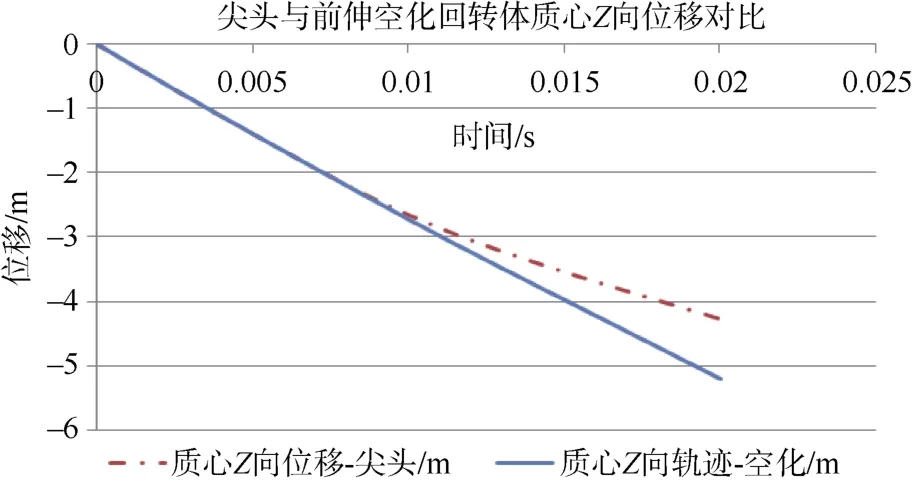
图14 尖头与前伸空化回转体质心Z向位移对比Fig.14 Comparison of centroid displacement in Z-dirction between pointed-head self-spin body and self-spin forward-extended cavitating body

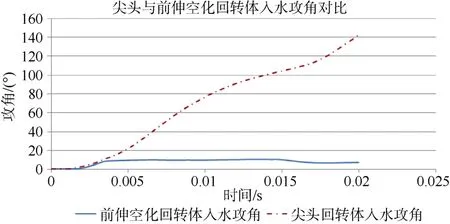
图15 尖头与前伸空化回转体入水攻角对比Fig.15 Comparison of attack angle for the self-spin body between pointed-head self-spin body and self-spin forward-extended cavitating body

图16 前伸空化回转体入水中侧视状态Fig.16 Side view of self-spin forward-extended cavitating body in the course of water entry

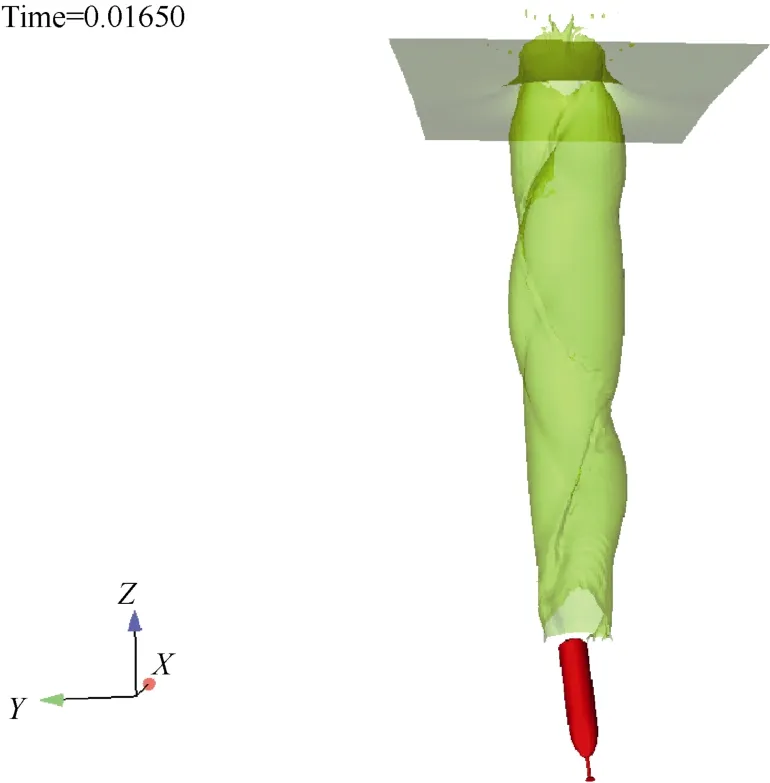
图17 前伸空化回转体入水中前视状态Fig.17 Front view of self-spin forward-extended cavitating body in the course of water entry

5 结束语

本文采用Lagrange结构网格和Euler 流场网格耦合的方法，对尖头回转体和前伸空化回转体高速自旋倾斜45°入水初始弹道进行了数值模拟。仿真结果表明：尖头回转体初始弹道入水后很快发射偏转，入水3 m后攻角超过90°，出现严重的姿态失稳。前伸空化回转体入水4 m深度范围内速度衰减较小，初始弹道稳定，攻角有轻微变化后趋于稳定。前伸空化回转体具有较高的水下弹道稳定性。