激光在小尺度湍流场中的透射功率模型

郭媛媛，王运鹰，李大伟，金方圆

（水下测控技术重点实验室，辽宁 大连116013）

0 引言

本文基于比尔-朗伯定律分析理论，对螺旋桨粒子尾流进行了仿真模拟，分别对激光通道内任意等体积区域粒子浓度时域变化特性、同一区域粒子浓度一维空域特性进行了分析；结合水下光学传输理论，通过曲线拟合，建立了激光在小尺度湍流区域传输的数理模型；采用532 nm蓝绿激光作为入射光源，对激光在小尺度湍流场流中的传输模型进行了水池实验验证。

1 理论

光在含有悬浮粒子的水中传播时，因传输介质的吸收和散射作用，在其传播路径上能量不断地衰耗。光通过距离为z=z1-z0区域后的光通量密度表示式[1-2]为

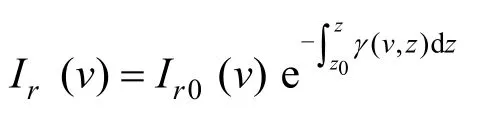
式中：Ir0(v)表示在入射面z0处的通量密度；Ir(v)是入射到dz所有面上的通量密度，是频率v的函数；指数中称为光学厚度；γ(v,z)是一个比例因子，称为消光系数或衰减系数[3]，是光频v和距离z的函数。通常把衰减系数分为吸收系数和散射系数2部分之和[4]，对于本文要研究的532 nm激光而言，有：

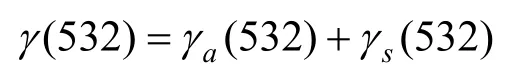
式中，γa和γs分别称为吸收系数和散射系数。含有悬浮粒子的水体散射主要包含纯水散射γw（v）和悬浮粒子散射γl（v）这2部分。

由于悬浮粒子的粒子尺寸与光的波长相近，因此悬浮粒子散射特性可以采用 Mie氏散射理论处理。对于532 nm的蓝绿激光，在距离z处的散射面上的散射强度为

当散射角不大于 5o时，模拟计算出粒子均匀分布条件下，粒径为10～300 μm范围的悬浮粒子激光（532 nm）散射系数与质量浓度的关系式为[5-7]

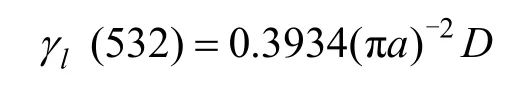
式中：a为粒子半径，m；D是水中粒子的质量浓度，mg/L。

水体对532 nm激光的透射率T（z）表示为[8]

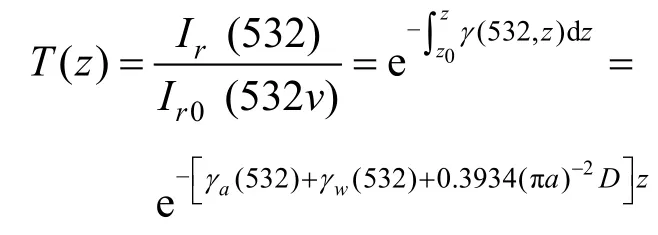
式中，γw(532)为水体散射系数。

2 数值模拟

2.1 几何建模

采用 FLUENT软件进行水中螺旋桨粒子尾流场的模拟仿真，基于混合网格技术划分螺旋桨扰动流场的全域网格模型。螺旋桨周围采用非结构网格，保证模型周围的网格密度，有利于提高流场细节的计算精度，在其他区域采用结构网格。在此基础上，采用分区和局部加密网格技术来保证局部敏感区域的网格数量。旋转域和固定区域之间的重叠面设置为滑移壁面，桨叶、桨毂以及鳍叶定义为无滑移的固壁条件。几何模型的相关参数设置如表1，边界条件设置如表2。数值模拟采用在流场中插入悬浮粒子的方法，液体作为连续介质，悬浮粒子群的运动采用离散相模型；将粒子分布在速度入口表面，悬浮粒子相关参数设置如表3所示。

表1 几何模型的相关参数设置Table 1 Related parameter settings of geometric model

表2 几何模型的边界条件设置Table 2 Boundary condition settings of geometric model

表3 悬浮粒子相关参数设置Table 3 Related parameter settings of suspended particles

2.2 数理模型

依据上述理论和参数设置，模拟计算了任意等体积区域粒子浓度时域特性和等体积区域粒子浓度一维空域特性。图1为距离螺旋桨不同位置等体积区域粒子浓度随时间的变化曲线，图2为同一区域不同时刻粒子浓度随距离的变化曲线。

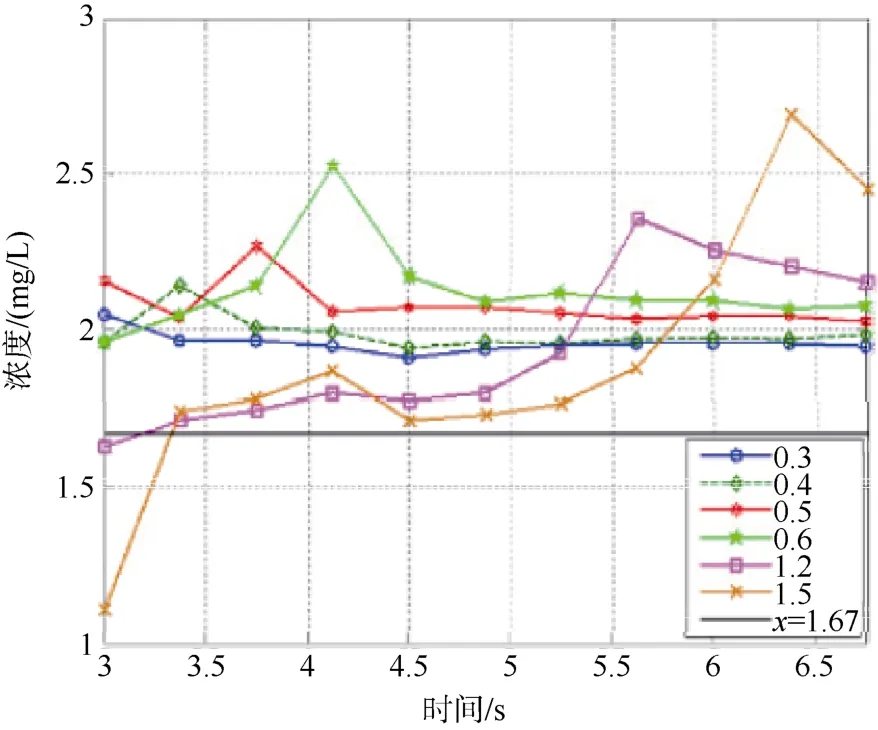
图1 螺旋桨不同位置同一体积区域内颗粒浓度随时间的变化曲线Fig.1 Variation curve of particle concentration with time in the same volume region at different positions from the propeller

图1结果显示：距离螺旋桨分别为0.3～0.6 m处等体积流场区域内，悬浮粒子质量浓度随时间变化较为平缓，均值高于流场初始质量浓度；距离螺旋桨较远的2个区域（距离1.2 m、1.5 m），粒子质量浓度随时间变化剧烈，这是由于在距离螺旋桨较远的流场区域，存在尺度交大、旋转较快的涡旋结构导致的。图2结果显示：距离螺旋桨0.3～1.1 m区域内，沿流场方向，不同时刻的粒子质量浓度随距离均呈现出相对随机的变化，变化范围集中在1.5～2.5 mg/L。

取激光发射端为起点，沿运动方向距螺旋桨（0.3+δL）m的截面生成特征线作为激光传输通道，激光通道垂直于螺旋桨中轴线，激光通道截面为S（z），通道长度选为0.8 m。假设湍流场的最小尺度远小于激光束截面S（z），激光束发散角为θ，激光传输距离为z，Ar为接收系统有效孔径面积，η表示系统通光效率，T（z）为水体透射率，那么距离Z处接收系统接收的透射功率可表示为

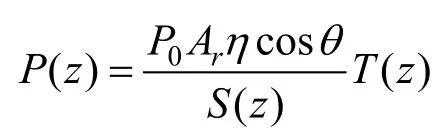
根据激光通道内粒子质量浓度时间特性仿真结果，曲线拟合出小尺度湍流区域粒子质量浓度方程，结合以上理论公式，得出激光在小尺度湍流场传输数理模型：

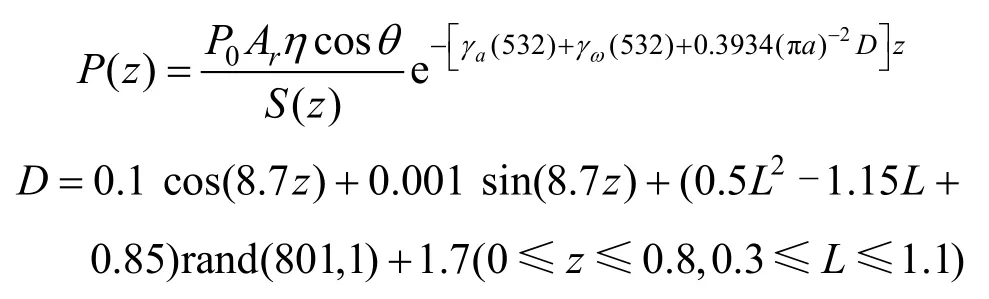
由此计算出仿真湍流场扰动前后激光透射功率的比值为

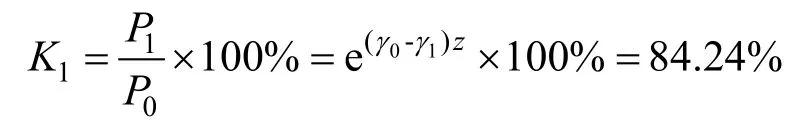
3 验模实验

实验采用激光前向测试系统，实验装置如图3所示，参数设置如表4所示，实验结果如图4、图5所示。

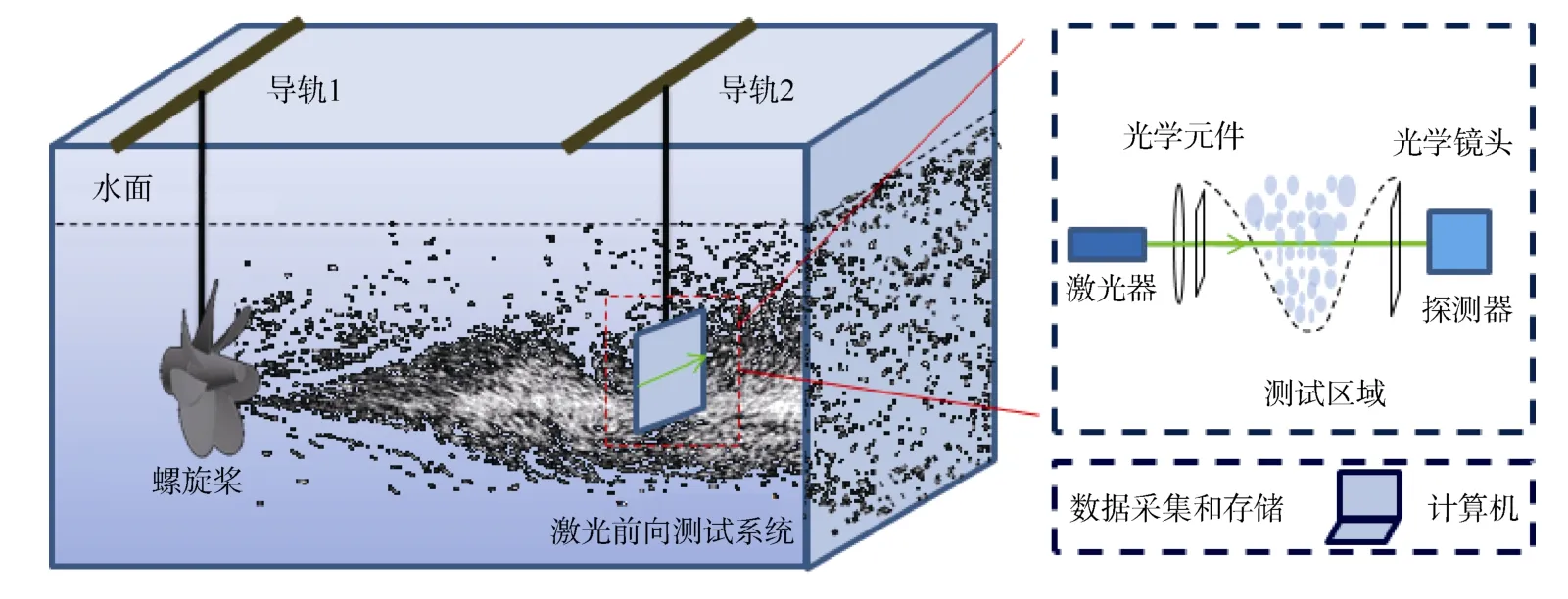
图3 实验装置图Fig.3 Experimental device diagram

表4 参数设置Table 4 The geometric parameters of experiment

图4、图5分别为静水环境激光透射强度和螺旋桨粒子尾流中激光透射强度随时间的变化曲线。由时域图分析发现：当流场稳定后，透射信号强度呈现出相对稳定的震荡。激光透射信号时域图上出现了向下的吸收峰，这些吸收峰来自传输介质中的悬浮粒子和微尺度气泡对光产生了强散射，导致透射方向的能量降低。

图4 静水环境下激光传输的时域特性Fig.4 Time domain characteristics of laser transmission in hydrostatic environment

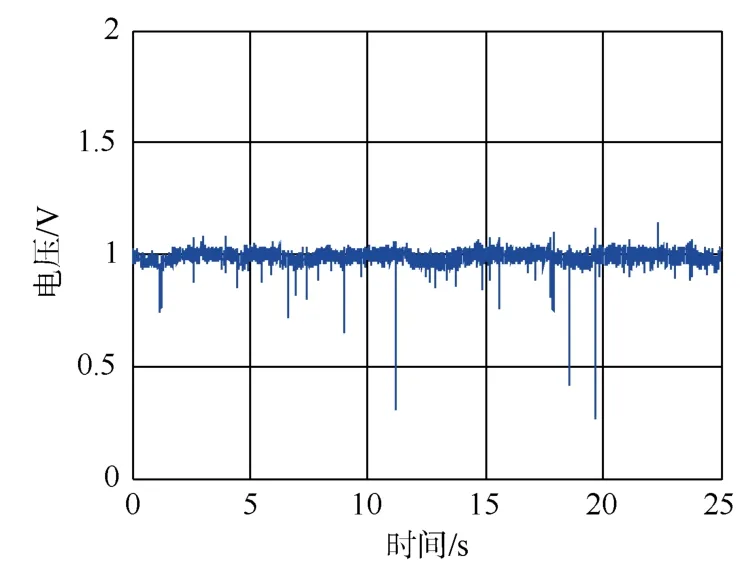
图5 螺旋桨粒子尾流中激光透射强度随时间的变化曲线Fig.5 Variation curve of laser transmission intensity with time in particle wake of propeller

表5 激光传输功率比Table 5 Ratio of laser transmission power

理论模型与实验的偏差σ根据公式σ=计算，结果如图6所示。

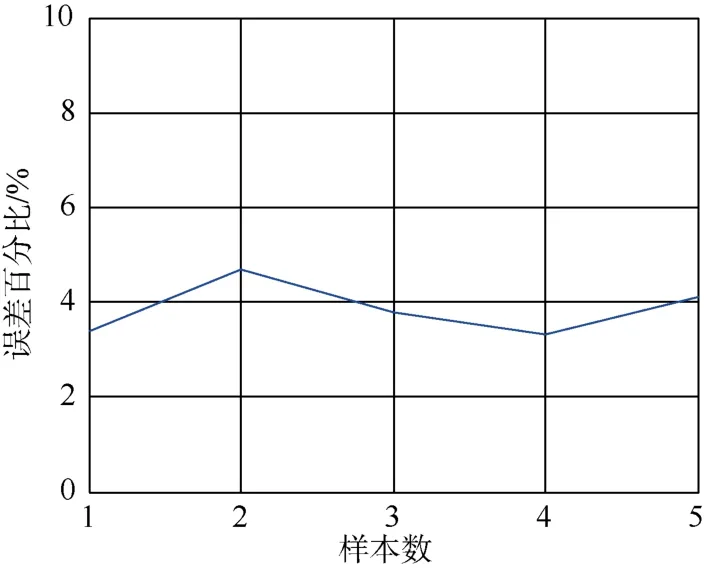
图6 理论模型与实验的偏差Fig.6 Deviation of theoretical model and experiment

由计算结果可知，理论模型与试验的偏差范围小于10%。水池试验在一定程度上验证了小尺度湍流场激光传输模型的正确性。只是该模型的精确性和通用性还需后期大量的试验进行验证和完善。

4 结束语

本文通过对螺旋桨粒子尾流中激光传输特性进行仿真模拟及实验研究发现，悬浮粒子质量浓度会影响激光在水下小尺度湍流场的传输透射特性；建立的数理模型能够较好地反映小尺度湍流场中激光传输透射特性与悬浮粒子质量浓度之间的关系，该模型的精确性和通用性还需后期大量实验进行验证和完善。