考虑顾客取货半径的电动汽车路径优化与服务策略研究

郭 放，黄宏军，杨 珺

考虑顾客取货半径的电动汽车路径优化与服务策略研究

郭 放，黄宏军，杨 珺

（华中科技大学管理学院，湖北 武汉 430074）

在环境意识增长与政府政策支持的有利条件下，电动汽车在物流行业得到良好的发展机遇。有电动汽车参与的物流服务需要配送人员、电动汽车和顾客在预定服务策略下共同完成。为提高物流服务的效率与质量，物流企业采取顾客自行取货与配送人员送货上门相结合的服务策略，在提高物流企业配送人员与车辆服务效率的同时，实现部分顾客对收货时间的个性化要求、减少不确定因素对后续配送服务造成不良影响的几率、提高服务水平。本文提出了以电动汽车作为物流配送车辆的考虑顾客自行取货策略的服务站点选址与车辆路径问题，并构建了整数规划数学模型。其次，给出了基于改进节约算法和禁忌算法的混合启发式算法MCWSA-TS。随后通过多组中、小规模算例验证了算法的有效性。最后，采用多组算例分析了覆盖策略与覆盖半径对运营成本的影响。实验结果表明，考虑顾客取货半径的多样化服务策略可以减少物流企业对配送人员与物流车辆的需求，缩短配送距离，进而降低运营成本。

电动汽车；选址-路径问题；混合启发式算法；多样化服务策略；半径覆盖问题

0 引言

在环境意识增长与政府政策支持的有利条件下，电动汽车在物流行业得到良好的发展机遇。城市内小件物流配送服务处于物流环节的末端，通常是由配送人员将快件从区域配送中心送达顾客处。由于顾客分散、市内交通情况复杂以及服务过程存在的诸多不确定因素影响，服务过程产生的成本以及占用的服务资源占到整个物流环节的35%-60%[1]。其中，配送人员与车辆数目、服务路径选择、物流服务时间以及顾客签收效率等因素都会影响企业物流成本与顾客满意度水平。收货地点周边交通状况与停车条件为物流服务时间增添了不确定因素，难以预测且不可控的顾客收货效率也会阻碍配送计划的顺利执行。除上述不确定因素以外，物流服务水平还与可使用车辆数目、服务路径设计等相互影响。缩短车辆配送路径，减少待服务节点（顾客点）有助于提高服务质量，减少顾客点之间相互影响的机会。但是，物流车辆的车载容量没有得到充分利用，可能导致车辆与人员成本的显著提升。另一方面，物流企业希望充分利用车辆载重量，使其在一条配送路径中服务更多顾客点。一旦在某一顾客点处产生延误，路径中后续顾客的配送时间均会受到影响，从而影响到整体服务水平。由此可见，高效的物流配送服务需要配送人员和顾客在预定服务策略下协作完成。因此，物流企业希望在提高物流企业配送人员与车辆服务效率的同时，实现部分顾客对收货时间的个性化要求、减少不确定因素对后续配送服务造成不良影响的几率、提高服务水平。为实现这一目的，部分物流企业采用了在顾客密集区域开设顾客自行取货服务站点的服务模式。位于站点服务区域内的顾客可自行前往服务站点取回货物，而对于位于站点服务半径之外的顾客则由物流车辆直接将其所需货物送至顾客处。例如，阿里巴巴旗下大型物流服务平台菜鸟驿站已经开设了超过40000个物流服务站点为在淘宝和天猫（阿里巴巴旗下网上购物平台）网购商品的顾客提供包裹免费保管服务。目前，菜鸟驿站服务站点主要包括校园菜鸟驿站、社区便利店、物业、连锁超市、邮局报刊亭等。此外，京东也采取了类似策略开设京东派服务点。目前，京东派主要集中在全国范围内本科院校和专科院校。顾客自行取货服务模式的整体成本不仅取决于配送成本、服务站点成本，还与顾客节点、站点备选位置的空间分布情况相关。尤其在本文采用电动汽车作为物流车辆的情形下，电量不足时物流车辆需前往服务站点充电或更换电池，服务站点选址直接影响配送路径策略。

本文基于站点的覆盖思想与顾客自行取货策略，研究了在顾客自行取货与送货上门相结合的多样化服务策略下的电动汽车服务设施选址与服务路径优化问题(Cover-EV-LRP)。Cover-EV-LRP由Dantzig等[2]提出车辆路径问题(VRP)延伸而来，VRP问题研究内容为指派位于起点的车队为所有顾客点提供服务，使得目标函数(例如配送距离、配送时间或其他成本)最小。带有容量约束的车辆路径问题CVRP要求所有车辆从起点出发完成服务任务后回到出发点，且车辆配送货物总量不得超过其最大载重量。 Baldacci等[3]分别在单一起点和多起点情形下采用精确算法研究了带容量限制的多车型车辆路径问题。Rivera J C，Afsar H M 等[4]研究了允许车辆带有累积载重量限制的VRP问题，并针对该问题提出了基于迭代邻域搜索的启发式算法。Jin J，Crainic T G等[5]提出了一种改进合作并行的启发式算法求解带有容量约束的VRP问题。上述研究均要求路径网络节点不能被同一车辆多次访问。然而，在现实生活中广泛存在如下情况：一辆配送车辆在服务若干顾客后再次前往之前去过的服务站点补充电量。允许服务站点为同一配送车辆提供多次充电服务有助于降低站点开设成本与车辆行驶成本。本文在1.3节拓展模型中考虑了同一车辆多次到访同一站点的情况，并对模型进行了相关改进。随着VRP 相关问题的拓展研究逐步深入，由于时间、成本或其他资源(例如车辆数量或里程等)限制，车辆无法或者没有必要到达每个网络节点的情形引发了部分学者的关注与探究。Current等[6]首次在旅行商问题(TSP) 中加入了“覆盖(Cover)”这一概念，未被车辆直接访问的顾客节点的需求由车辆送达覆盖其的服务点，顾客需自行前往服务点取货。至此，该问题由TSP拓展为CSP问题。CSP问题致力于构建一条尽可能短的哈密顿回路为顾客提供服务，要求未在回路上的顾客与至少一个在回路上的顾客的距离小于事先给定的覆盖半径(顾客自行取货半径)。Salari，Naji-Azimi等[7]提出基于邻域搜索的启发式算法求解CSP问题。Hachicha等[8]将“Cover”引入VRP问题(Cover-VRP)，指派多组车辆分别构造哈密顿回路为顾客提供服务。Ha M H，Bostel N等[9]采用一种精确算法(分支切割算法)求解Cover-VRP问题。上述文献提出的模型均建立在所有顾客点的需求量必须为1的基础上，不能体现出实际操作中顾客点的差异化需求。也没有考虑车辆最大载重容量限制，而是退而求其次约束每条线路最大顾客数量。此外，上述文献均没有涉及到车辆在途补充能源等问题（加油或充换电池）。本文构建的数学模型允许车辆在服务过程中根据电量需求前往站点补充电量。模型考虑了车辆容量约束，顾客需求量为不小于1的整数，且每条线路的顾客需求量不超过车辆最大载重量。

与此同时，电动汽车具有的清洁环保等特点促使其在城市物流配送领域日益受到重视，并得到越来越多的推广与应用[9]。各级政府部门相继出台多项促进电动物流汽车及其相关产业快速发展的政策与建议，为电动物流汽车市场的拓展与相关服务设施网络的完善提供保障。与传统燃油汽车不同，电动物流汽车依靠车载电池为其提供动力，车辆需在电量耗尽之前前往电动汽车服务设施为电池充电或者更换电池。兼顾电动物流车辆的充、换电需求与顾客的配送需求，统筹规划服务设施选址与配送路径策略有助于提高物流服务效率降低成本，该问题也成为了近年来业界与学术界的研究热点。Erdogan 等[11]首先提出绿色VRP的概念(Green Vehicle Routing Problem，GVRP)，建立起以车辆行驶距离成本最小为目标函数的数学模型，随后提出一种改进C-W节约算法探索此问题的满意解。Schneider等[12][13]在其研究中对电动汽车中途停站充电问题的模型及其求解方法进行了探讨，并基于禁忌搜索与变邻域搜索提出了一种求解此类问题的高效率混合启发式算法。Yang Jun 和 Sun Hao[14]研究了在采用更换电池模式的情形下电动物流汽车服务设施网络和车辆路径优化策略，随后，采用基于禁忌搜索和大邻域搜索的多阶段混合启发式算法对问题进行了求解。Keskin M 和 Catay B[15]研究了允许部分充电的电动汽车服务策略，车辆接受充电服务的时候可以根据实际需求来决定充电量与充电时间。Koc C等[16]将使用车辆数目作为优化对象之一。在车辆不受最大行驶里程约束的假设条件下，通过优化仓库选址和车辆路径策略降低企业资金投入。揭婉晨等[17]研究了多车型电动汽车车辆路径问题，并利用精确算法（分支定价算法）寻求问题最优解。以上文献可以看出，目前关于电动汽车车辆路径与设施选址问题的研究中尚未考虑覆盖策略，服务形式均为单一的送货上门。因此，本文将站点的覆盖思想应用于电动物流车辆选址与路径问题。研究了顾客自行取货与送货上门相结合的多样化服务策略下，将服务站点选址、配送路径设计与顾客服务策略选择作为优化对象的电动汽车配送路径问题。同一车辆在配送途中允许多次前往同一站点接受充电服务。开设的服务站点同时具备为车辆充电和暂存货物供顾客自行取货的功能，其覆盖范围内的顾客需求均通过车辆送达此处由顾客自行取货。未处于任何站点服务范围内的顾客由车辆送货上门。本文首先提出了Cover-EV-LRP模型，其由CVRP拓展而来，属于NP-hard问题。其次，基于改进节约算法以及禁忌搜索算法提出了一种名为MCWSA-TS的混合启发式算法用于模型求解。随后，将MCWSA-TS与CPLEX的计算结果进行对比，证实模型的准确性与算法的有效性。最后，对覆盖策略与相关参数对运营成本的影响进行了探讨。

1 问题描述及数学模型

1.1 问题描述

1.2 基础模型

基于上述条件, 数学模型如下：

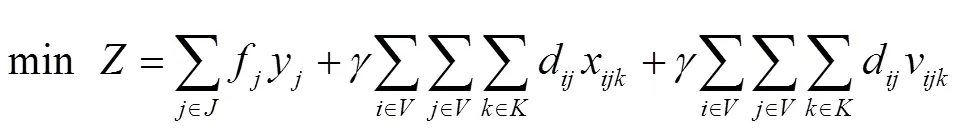
S.T.

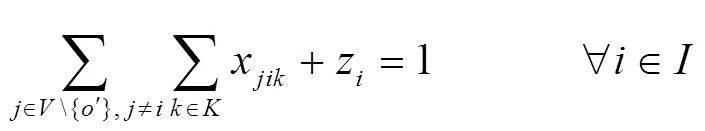
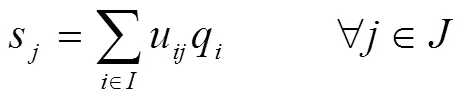
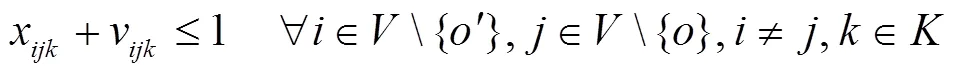
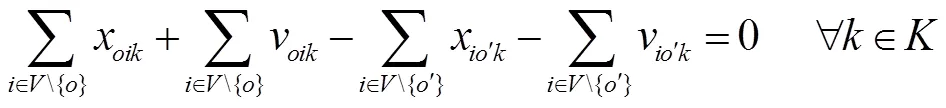
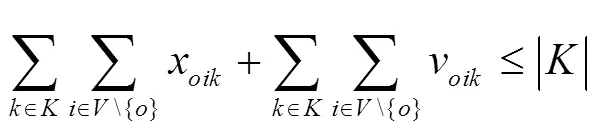
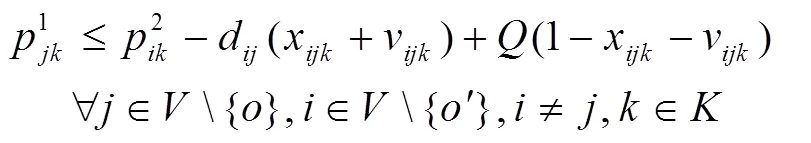
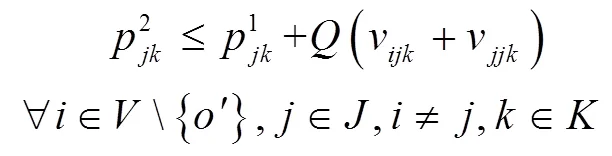
1.3 拓展模型

s.t.：(2)-(7)，(11)-(25)

1.4 拓展模型线性化

引理 1.

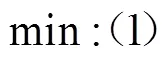
s.t.：(2)-(7),(11)-(25),(27)

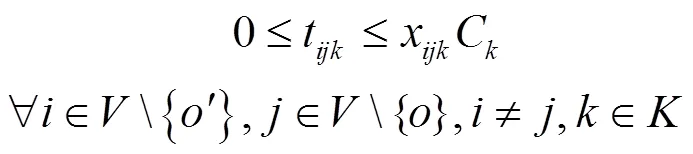
2 算法实现

2.1 初始选址

步骤2.2：计算服务站点覆盖的顾客点需求量总和并将其作为该站点的需备货量。

步骤2.3：更新顾客点集合，包括已开设的服务站点和未被任何服务站点覆盖的顾客点。

2.2 路径子问题

步骤1：（路径初始化）

2.3 优化当前解

步骤1(GA)：对于配送途中物流车辆前往充电站点次数不少于两次的服务线路，采用贪婪策略将其中一个站点移除，若在当前路径上行驶的物流车辆满足最大里程限制则更新当前路径。否则，保持原路径策略。

步骤2(LS)：采用点移动，点交换，点插入和局部交换策略进行局部搜索。

每次操作均要求满足车辆载重量和行驶里程约束。比较优化前后的目标函数解，并在满足条件时更新满意解与相应的目标函数值。4种搜索策略如下文所述。

（1）点移动策略的优化对象为任意一条服务路径。将路径中的每一个点从当前位置移动到同一路径中的其他位置。

（2）点交换策略的优化对象为任意一对服务路径。从两条路径中分别选取一个点将其放入另一条配送路径中，交换点在新路径中的服务顺序为使得行驶距离增加量最小的服务顺序。

2.4 禁忌搜索

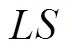
步骤3：重复执行步骤2，直到迭代次数达到预定最大次数为止。随后，执行步骤4。

3 实验结果及分析

3.1 测试用例

3.2 实验结果与分析

3.2.1模型与算法的验证分析

表1 CPLEX与MCWSA-TS结果对比

3.2.2 多样化服务策略影响性分析

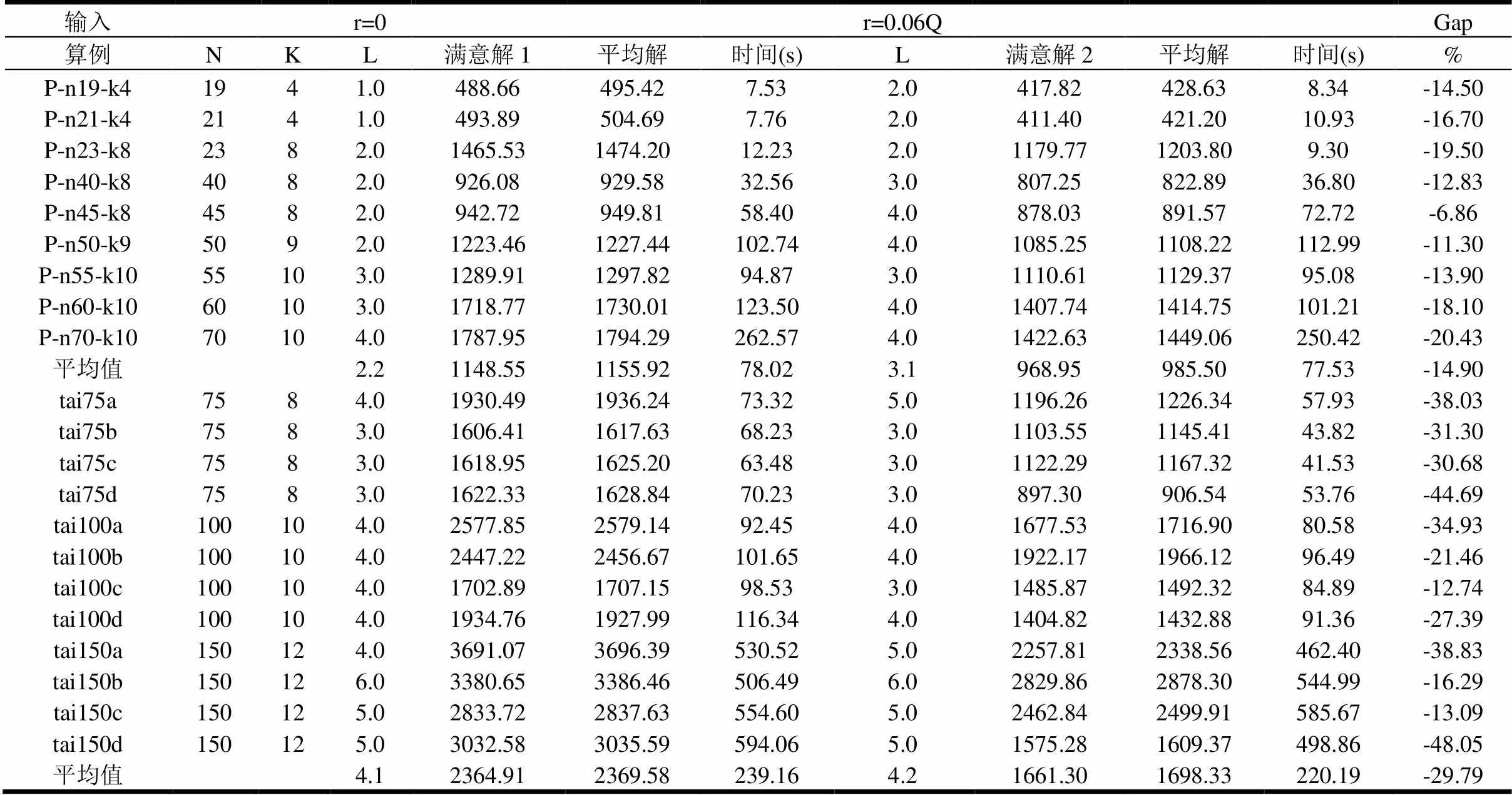
表2 多样化服务策略实验结果对比

图1 路径成本对比

Figure 1 Comparison of path cost

图2 配送所需车辆数对比

Figure 2 Comparison of vehicle amount required for distribution

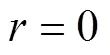
3.2.3 服务半径敏感性分析

表3 服务半径敏感性实验结果对比

表4 服务半径敏感性实验结果对比2

图3 配送线路示意图

图4 配送线路示意图

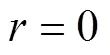
4 结束语

近年来，电动汽车在物流行业得到良好的发展机遇。以电动汽车作为物流配送车辆的考虑顾客自行取货服务模式的站点选址与车辆路径问题是一个应用前景广泛的现实问题。电动汽车参与的物流配送服务需要配送人员、配送车辆和顾客在预定服务策略下共同完成。尤其在本文采用电动汽车作为物流车辆的情形下，电量不足时物流车辆需前往服务站点充电或更换电池，服务站点选址直接影响配送路径策略，这也进一步增加了问题的复杂性。物流企业出于提高配送人员与服务时间等资源的利用率、降低运营成本提高顾客满意度水平的目的，采用了在顾客密集区域开设顾客自行取货服务站点的服务模式，服务站点可为顾客提供包裹代收及暂存服务。服务站点有相应的服务范围，位于站点服务区域内的顾客可自行前往服务站点取回货物，而对于位于站点服务半径之外的顾客则由物流车辆直接将其所需货物送至顾客处。开设站点提供顾客自行取货服务既有助于物流企业降低运营成本，又能满足部分顾客对收货时间的个性化要求、减少不确定因素对后续配送服务造成不良影响的几率。基于顾客自行取货与配送人员送货上门的多样化服务策略，本文提出了考虑站点覆盖的电动汽车路径优化与换电策略问题，建立了该问题的整数规划数学模型并且给出了基于改进节约算法与禁忌算法结合的混合启发式算法MCWSA-TS。

为了提高资源利用率与服务效率，物流运营方需要统筹兼顾，通过科学的方式权衡多样化服务策略涉及到的多方面成本。实验结果表明：（1）在顾客自行取货与送货上门服务策略下，在顾客集中的区域设立服务站点有助于物流企业获得较好的成本效益；（2）受益于服务策略的多样化，需送货上门的顾客数量减少有助于降低配送所需车辆数目(配送人员数目)，进一步降低企业运营成本；（3）在服务站点覆盖半径较大的情况下，自行取货的顾客点数目较多有助于降低整体运营成本。但是在现实生活中，需要进一步考虑自行取货距离过长可能会导致的顾客流失问题；（4）受到顾客点空间分布差异的影响，拥有相同顾客节点数量的不同算例在相同服务半径下的服务策略与运营成本存在差异；（5）在顾客点与充/换电站点数量相对较少的情况下，为了供顾客自行取货而专门开设服务点产生的成本抵消了自行取货策略节省的部分配送成本，建站数量增加直接导致成本降低幅度减少。随着服务网络规模扩大，服务站点的选择需要协调物流车辆充/换电需求与顾客自行取货节省的配送成本。逐渐增多的站点数量也为两者的统筹选址提供了更多的选择，减少为顾客自行取货而专门开设服务站点的几率。通过协调站点的位置同时满足车辆充/换电需求与顾客取货需求，实现Cover-LRP效益的最大化。

以下方面还有待进一步研究，本文所考虑的配送车辆为单一车型，在未来的研究中可以进一步分析多车型情况下的路径与服务策略；其次，设计更加高效的算法策略将是未来工作的一个重点。

[1] Wasner M, Zapfel G. An integrated multi-depot hub-location vehicle routing model for network planning of parcel service[J]. International Journal of Production Economics, 2004, 90(3): 403-419.

[2] Dantzig G B, Ramser J H. The truck dispatching problem[J]. Management science, 1959, 6(1): 80-91.

[3] Baldacci R, Mingozzi A. A unified exact method for solving different classes of vehicle routing problems[J]. Mathematical Programming, 2009, 120(2): 347-380.

[4] Rivera J C, Afsar H M, Prins C. A multistart iterated local search for the multitrip cumulative capacitated vehicle routing problem[J]. Computational Optimization and Applications, 2015, 61(1): 159-187.

[5] Jin J, Crainic T G, Lokketangen A. A cooperative parallel metaheuristic for the capacitated vehicle routing problem[J]. Computers & Operations Research, 2014, 44: 33-41.

[6] Current J R, Schilling D A. The covering salesman problem[J]. Transportation science, 1989, 23(3): 208-213.

[7] Salari M, Naji-Azimi Z. An integer programming-based local search for the covering salesman problem[J]. Computers & Operations Research, 2012, 39(11): 2594-2602.

[8] Hachicha M, Hodgson M J, Laporte G, et al. Heuristics for the multi-vehicle covering tour problem[J]. Computers & Operations Research, 2000, 27(1): 29-42.

[9] Ha M H, Bostel N, Langevin A, et al. An exact algorithm and a metaheuristic for the multi-vehicle covering tour problem with a constraint on the number of vertices[J]. European Journal of Operational Research, 2013, 226(2): 211-220.

[10] Chellaswamy C, Ramesh R, Rau C V. A supervisory control of a fuel free electric vehicle for green environment[C] Emerging Trends in Electrical Engineering and Energy Management(ICETEEEM), Chennai: IEEE, 2012-06-15,S.l.:s.n.,2012: 387-393.

[11] Erdoan S, Miller-Hooks E. A green vehicle routing problem[J]. Transportation Research Part E: Logistics and Transportation Review, 2012, 48(1): 100-114.

[12] Schneider M, Stenger A, Goeke D. The electric vehicle-routing problem with time windows and recharging stations[J]. Transportation Science, 2014, 48(4): 500-520.

[13] Schneider M, Stenger A, Hof J. An adaptive VNS algorithm for vehicle routing problems with intermediate stops[J]. OR Spectrum, 2015, 37(2): 353-387.

[14] Yang J, Sun H. Battery swap station location-routing problem with capacitated electric vehicles[J]. Computers and Operations Research, 2015, 55: 217-232.

[15] Keskin M. Partial recharge strategies for the electric vehicle routing problem with time windows[J]. Transportation Research Part C: Emerging Technologies, 2016, 65: 111-127.

[16] Koc C, Bektas T, Jabali O, et al. The fleet size and mix location-routing problem with time windows: Formulations and a heuristic algorithm[J]. European Journal of Operational Research, 2016, 248(1): 33-51.

[17] 揭婉晨, 杨珺, 杨超. 多车型电动汽车车辆路径问题的分支定价算法研究[J]. 系统工程理论与实践, 2016, 36(7): 1795-1805.

Jie W C, Yang J, Yang C. Branch-and-price algorithm for heterogeneous electric vehicle routing problem [J]. Systems Engineering —Theory & Practice, 2016, 36(7): 1795-1805.

[18] Jie W C, Yang J, Yang C. Branch-and-price algorithm for heterogeneous electric vehicle routing problem[J]. Systems Engineering- Theory & Practice, 2016, 36(7): 1795-1805.

[19] Clarke G, Wright J W. Scheduling of Vehicles from a Central Depot to a Number of Delivery Points[J]. Operations Research, 1964, 12(4):568-581.

[20] Fan L, Qin Q. The Optimization Model and Empirical Analysis for Vehicle Routing Problems with Time Windows Based on C-W Algorithm[M]. LISS 2012. Springer Berlin Heidelberg, 2013:253-258.

[21] Wang Z, Li Y, Hu X. A heuristic approach and a tabu search for the heterogeneous multi-type fleet vehicle routing problem with time windows and an incompatible loading constraint[J]. Computers & Industrial Engineering, 2015, 89(C):162-176.

[22] Lai D S W, Demirag O C, Leung J M Y. A tabu search heuristic for the heterogeneous vehicle routing problem on a multigraph[J]. Transportation Research Part E Logistics & Transportation Review, 2016, 86:32-52.

[23] Silvestrin P V, Ritt M. An iterated tabu search for the multi- compartment vehicle routing problem[J]. Computers & Operations Research, 2017, 81:192-202.

[24] Soto M, Sevaux M, Rossi A, et al. Multiple neighborhood search, tabu search and ejection chains for the multi-depot open vehicle routing problem[J]. Computers & Industrial Engineering, 2017, 107: 211-222.

[25] Woensel T V. Vehicle Routing Problem with Stochastic Travel Times: Balancing Service and Transportation Costs[J]. Computers & Operations Research, 2017, 40(1):214-224.

[26] Augerat P, Belenguer J M, Benavent E, et al. Computational results with a branch and cut code for the capacitated vehicle routing problem[J]. Rapport de recherche- IMAG,1995.

[27] Rinaldi G,Yarrow L A. Optimizing a 48-city traveling salesman problem: A case study in combinatorial problem solving[M]. New York University, Graduate School of Business Administration,1985.

[28] Taillard E. Benchmarks for basic scheduling problems[J]. European journal of operational research, 1993, 64(2): 278-285.

Study on the electric vehicle routing optimization and service strategy with the consideration of customer self-pickup radius

GUO Fang, HUANG Hongjun, YANG Jun

( School of Management, Huazhong University of Science and Technology, Wuhan 430074, China)

With the favorable conditions of increasing environmental awareness and government support, there are good opportunities for electric vehicles to be employed in the development of the logistics industry. The logistics service of small packages in cities takes place at the end of the logistics chain, and these are usually delivered to customers by couriers from regional distribution centers. Owing to the scattered locations of customers, complex traffic situations, and uncertainties in the service process, the costs of the last mile delivery tour and its occupied service resources account for 35% -60% of the entire logistics link costs. Therefore, enterprises are eager to seek more favorable service strategies, and hope that this can help logistics enterprises to improve service times and the utilization rates of resources for couriers and reduce operating costs, as well as satisfying the personalized requirements of customers regarding delivery times, and reducing the adverse impacts of uncertain factors on follow-up delivery services to improve customer satisfaction levels.

In this paper, the site coverage concept and customer self-pickup strategy are applied to the facility location and electric vehicle routing problems. This paper studies the optimization of electric vehicle facility location and service strategies under a diversified service strategy combining customer service (within a service radius) and home delivery service (outside the service radius), and establishes a mathematical model of integer programming. The main differences between this research and existing research are: (1) The distribution service line is no longer limited to the Hamilton circuit, and this allows vehicles to accept charging/swapping services a number of times at the same service station. (2) Customers can access goods in a variety of ways, and they are no longer limited to courier delivery in a door-to-door service. (3) The service station can provide a battery charging/swapping service to electric vehicles. Customers who are in the service range of the station can pick up goods by themselves from there, while customers who are not in any service range can enjoy a home delivery service performed by the vehicles.

In the first part, the paper introduces the basics of electric vehicle routing optimization and service strategies, considering the manner of customer self-pickups, puts forward a reasonable restriction condition and hypothesis, defines the relevant parameters and decision variables, and establishes the corresponding integer programming model. This problem constitutes an expansion of the CVRP problem, and the high complexity makes it difficult to obtain a satisfactory solution in polynomial time. Therefore, in the second part this paper proposes a hybrid heuristic algorithm MCWSA-TS, based on a modified Clarke-Wright saving algorithm and the tabu search algorithm. MCWSA-TS is composed of four parts: the radius cover algorithm (RCA), modified Clarke-Wright saving algorithm (MCWSA), local search (LS), and tabu search (TS). The RCA is proposed to obtain an initial location solution and assignment strategy. Then, this paper adopts the modified savings mechanism to optimize the service line in the path subproblem. Finally, the current strategy is optimized by LS and TS. The third part presents the numerical experiments, and first introduces the set and value rules of the various parameters. In order to verify the accuracy of the model and the effectiveness of the heuristics algorithm, this paper uses IBM CPLEX12.6 to solve a series of small-scale examples, and compares the results with those of the hybrid heuristic algorithm MCWSA-TS. The experimental results show that MCWSA-TS can find satisfactory solutions of the problem in short times, and these solution are superior to those of CPLEX. Then, 21 groups of examples are selected for a comparative analysis, highlighting the impact of diversified services on the business strategy, service path cost, and the required number of vehicles (the number of couriers), in order to demonstrate its superiority. Finally, a sensitivity analysis on the service radius of the covering-LRP problem is conducted.

Electric vehicles; Location-routing problem; Hybrid heuristic algorithm; Diversified service strategy;Radius cover concept

2017-04-19

2017-10-30

Supported by the National Natural Science Foundation of China (71320107001), the Fundamental Research Funds for the Central Universities (2015QN175) and the Wuhan Modern Service Plan

U116.2；O221

A

1004-6062(2020)01-0154-010

10.13587/j.cnki.jieem.2020.01.017

2017-04-19

2017-10-30

国家自然科学基金重大资助项目（71320107001）；中央高校基本科研业务费专项资助（2015QN175）；武汉市黄鹤英才（现代服务）计划资助项目

郭放（1990—），男，四川江油人；华中科技大学管理学院，博士研究生；研究方向：网络优化。

中文编辑：杜 健；英文编辑：Charlie C. Chen