锥形非固结隔震支座理论模型参数试验研究及其结构地震响应分析

何文福，曾一峰，许 浩，刘文光，冯德民

(1.上海大学土木工程系，上海 200072；2.藤田技术中心，日本厚木 243-0125)

减隔震技术作为一种能有效降低地震反应的手段，在日本、美国和智利等地震多发国家得到了广泛应用[1]。隔震支座作为发展最为成熟的减隔震技术之一，通过延长结构的周期来降低上部结构的地震响应。随着我国抗震设防要求的提高，高烈度区所占国土面积的比例也随之提高[2]。而我国广大村镇住宅的抗震能力偏弱。历次震害表明，在遭受相同震级的情况下，其破坏程度普遍比较严重[3]。常用的隔震支座如橡胶支座、滑板支座等，因成本昂贵和施工复杂的特点，不利于在经济落后、技术薄弱的村镇地区推广。

为解决广大高烈度地区村镇房屋的抗震能力不足的问题，大量学者提出了新型的减隔震技术。Kelly[4]在 21世纪初提出用纤维增强复合材料代替橡胶支座中的钢片，以减轻支座重量且形状可按需切割。已有学者对该纤维板橡胶隔震支座在各类粘结情况下的隔震性能进行了试验[5－7]。Tsang等[8－9]提出了废旧轮胎橡胶-土混合隔震层，可同时降低水平和竖向的地震响应。Nanda等[10]研究了土工布作为摩擦滑移材料在地震作用下的耗能效果。国内，谭平等[11]提出了工程塑料板橡胶支座，对支座的各项性能进行了系统研究，并提出了施工方法。陈彪汉等[12]提出一种利用废旧轮胎片的叠层隔震支座，比较了不同层数及设计压应力下的竖向力学性能。孟庆利等[13]提出了铅芯废旧轮胎隔震垫，比较了该隔震垫与废旧轮胎隔震垫的竖向和水平力学性能。曹万林等[14]提出了一种以玻璃珠代替粗砂的基础滑移隔震技术。尚守平等[15]提出了钢筋-沥青复合隔震层，进行了隔震层在不同工况下的振动台试验，表明减震效果显著且有位移限制能力。袁康等[16]在考虑极寒情况下，提出砂垫层-基础滑移复合隔震体系。虽然在村镇房屋抗震减灾领域已经引入了减隔震思想与技术，针对低层及多层村镇房屋仍需一种低价高效的隔震支座。

除了上述所提，常用的隔震支座也存在大震下位移变形过大、支座丧失功能及结构容易发生碰撞及倾覆等问题，在 2016年日本熊本地震中橡胶隔震结构就存在损伤破坏现象。村镇地区的房屋主要为低层及多层[17]，总高度和高宽比相对较小。对此本文提出一种构造简单、便于施工、造价可接受的锥形隔震支座，建立了水平刚度的计算公式和力-位移模型，并通过静力试验进行验证和影响因素分析，针对支座提出了在不同场地条件下的高宽比限值，探讨了支座设计参数的改变对其隔震结构的地震响应规律。

1 锥形非固结支座构造及理论模型

锥形支座构造及实物见图1(a)和图1(c)，支座由上凹盖板、粘弹性材料、下凸盖板组成，如图1(b)所示。盖板的锥形设计是防止地震过程中发生过大水平位移。支座的粘弹性材料位于盖板之间且均无粘结，省去普通支座加工中橡胶与钢板之间的粘结硫化过程。通过上下盖板与粘弹性材料的相对运动，达到消耗地震能量的目的。

图1 锥形非固结支座实物及构造图Fig.1 Schematic and physical design diagram of non-consolidation tapered bearing

1.1 支座运动状态

根据锥形非固结支座的构造，其变形状态为中间层橡胶的水平剪切、滑动摩擦及斜向压剪变形 3个阶段，如图2(a)所示。上述阶段盖板与橡胶之间竖向无脱离。地震耗能主要分为两部分，盖板与中间夹层橡胶的滑动摩擦耗能和斜面橡胶受盖板水平压剪的变形耗能。在地震较小时，上、下盖板在水平方向上发生相对的水平剪切橡胶的运动；当水平地震作用足够大时，上盖板克服摩擦力开始沿水平方向滑动。水平滑动完成后，上盖板运动至斜面时，开始挤压并剪切斜面的橡胶。在地震较大时，上盖板有沿斜面抬升的趋势。地震能消耗完后，上盖板在结构自重作用下沿接触面复位。支座在上述过程中，消耗大量地震能。

1.2 支座水平刚度公式

1.2.1 水平剪切

在地震作用下，上下盖板的相对运动会与夹层的橡胶产生摩擦阻力从而剪切如图2(b)所示的橡胶面积。该水平刚度K1的计算式与橡胶支座单纯考虑橡胶层剪切刚度的公式相同[18]。

式中：G为橡胶的剪切弹性模量；A为在水平面上橡胶被盖板剪切的面积；T为橡胶厚度；d1由最大摩擦力确定。

图2 锥形非固结支座运动状态及理论模型Fig.2 Motion state and theoretical model of non-consolidation tapered bearing

1.2.2 滑动摩擦

在水平剪切过程中，盖板与橡胶的最大摩擦力被克服之后，盖板沿水平滑动耗能，如图2(a)所示。该过程位移与制造及安装过程中产生的初始间隙有关。

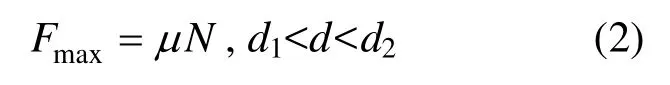
式中：μ为盖板与橡胶的摩擦系数；N为竖向加载力。根据竖向压应力，摩擦系数范围在0.1~0.38[19]。d2由支座构造、设计目标及地震动输入的性能决定。

1.2.3 斜面压剪

上盖板沿水平方向完成滑动摩擦之后，开始压剪斜面的橡胶。

由于压剪过程中受压剪面积随位移变化，取支座底部的水平面作为积分起始面。下凸盖板坡度角为θ，顶面半径为r，底面半径为R，斜面橡胶沿径向的水平长度为T＇，盖板的斜面长为L，盖板的水平位移为δ0。假定任意时刻的斜面压剪面积对应角度为φ，由于支座的构造特点，其范围在(-π/2,π/2)之间，如图2(c)所示；则由应力-应变关系及几何关系可得水平刚度积分式，再对φ进行积分可得。

式中：E为橡胶的弹性模量；d3由斜面橡胶的挤压极限确定，取橡胶厚度的60%。

上述过程根据上述公式，结合支座的运动方式，各阶段的力学关系见图2(d)。由支座往返运动完整过程可构建支座的理论本构关系图3。支座运动的完整过程如下：盖板先对水平部分的橡胶进行剪切，将初始间隙压缩完成后对斜面橡胶进行挤压，水平刚度由K1变至K2。在设计支座的过程中，平台面与斜面的接触面的差异使K1>K2。卸载时橡胶会逐渐复位，由于刚度较大的部分先回退，所以复位顺序先是水平部分的橡胶再到斜面橡胶，对应刚度变化从K1再到K2。当地震作用反向，水平面的橡胶先剪切，而滑动摩擦段位移是初始状态的两倍，之后支座变化与前述一致。

图3 锥形非固结支座力学模型Fig.3 Constitutive model of non-consolidation tapered bearing

2 支座力学性能试验

静力试验将对不同设计参数的试件进行分析。从上述三阶段运动状态及对应公式推导，坡度角、橡胶层厚度是影响锥形支座耗能表现的关键因素。选不同厚度橡胶层和坡度角盖板进行组合。除上述因素，还将考察支座在不同水平位移幅值和竖向压应力时的耗能。力学性能试验的内容包括坡度角、橡胶层厚度及种类、位移幅值及竖向压应力的影响。

2.1 试验概况

为了研究坡度角、橡胶层材料种类和厚度对支座耗能表现，本文设计加工了支座倾角分别为30°、45°、60°的3组盖板组合。取的两种不同橡胶材料：氯丁橡胶(Neoprene)和丁基橡胶(Butyl)。橡胶片形状为厚度均匀的矩形，尺寸略大于支座。试件以30°支座为例，详细尺寸见图4。由上述不同设计参数、位移幅值及竖向压应力共12种形式，见表1。

试验加载装置为水平极限加载±500 kN的电液伺服压剪系统，采用力控制加载。试验加载过程及装置见图5。

2.2 试验结果分析

为了探讨锥形支座整体的力-位移关系，采用等效刚度和等效阻尼的方式评估支座的整体性能。计算公式如式(4)和式(5)所示。

式中：keq为等效刚度；Q1为最大位移对应正向水平加载力；Q2为最小位移对应负向加载力；X1和X2别为最大位移和最小位移。

表1 支座试件设计参数Table 1 Design parameters of specimens

图4 支座上下盖板实体模型及设计尺寸Fig.4 Physical model and design dimensions of the upper and lower covers.

图5 电液伺服压剪试验布置图Fig.5 Electro-hydraulic servo testing schema

式中：ζeq为等效阻尼比；ΔW为单次循环下滞回环面积。

2.2.1 试验验证

图6为坡度角为45°试件在两种不同橡胶材料，分别在橡胶厚度为5 mm和10 mm的情况下，施加位移幅值5 mm的力-位移曲线与图3所提出的理论曲线进行对比。表2为理论计算所得刚度值与试验计算刚度值的对比结果。由图表可得，试验所得锥形支座的力-位移曲线呈现双锥形的特性，在橡胶层厚度较小时，理论曲线与试验曲线吻合较好，各阶段刚度变化趋势与预期一致；橡胶层厚度较大时，斜面压剪阶段的尖角段差异较大，是所加载位移幅值较小，斜面橡胶未充分变形所致。所得到厚层试件实测与理论值相差较大与文献的现象一致[20]。两种材料所形成的试验曲线基本一致，故下文仅采用氯丁橡胶的试验结果。

表2 理论计算刚度与试验数据对比Table 2 Stiffness comparison of theoretical and experimental values

2.2.2 坡度角相关性

对锥形支座在橡胶厚度为10 mm，水平加载位移为5 mm，竖向压应力为6 MPa时，给出了30°、45°、60°三种不同坡度角的试件的滞回曲线，见图7(a)。

从图7(a)可以看出，坡度角为 30°的支座试件所形成的滞回环面积最大，压剪阶段所形成的尖角最饱满。坡度角为 60°的支座试件所形成的滞回环面积最小，压剪阶段图形所形成的尖角较窄。即在相同橡胶厚度和加载的情况下，随着坡度角的增加其耗能能力减小，压剪阶段的水平刚度也随坡度角增加而增大。

图8(a)给出坡度角对隔震支座等效刚度、阻尼比的影响。从图中可以看出：1)坡度角的增大，隔震支座等效刚度增大；2)坡度角增大，支座试件阻尼比减小。由上可得，相同位移下选用较小的坡度角有利于耗能。

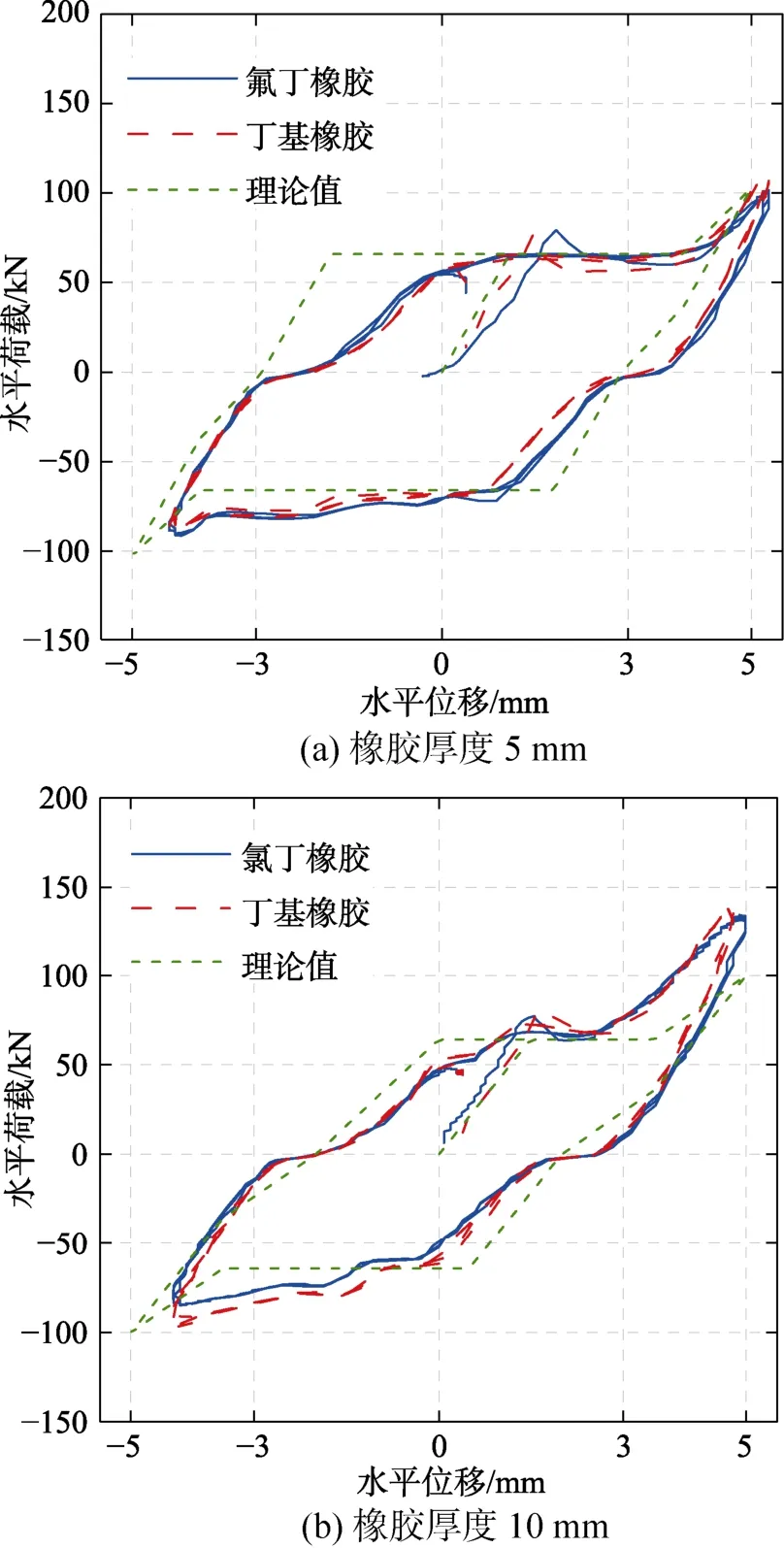
图6 试验曲线与理论力-位移曲线对比Fig.6 Comparison of test curve and theoretical force-displacement curve

2.2.3 橡胶厚度相关性

图7(b)给出了坡度角为 45°，水平加载位移为5 mm，竖向压应力为4 MPa情况下，不同橡胶层厚度对支座水平滞回曲线的影响。

由图可知，在坡度角较大，加载位移相同时，使用不同厚度橡胶层的试件所形成的滞回环曲线围成的面积随厚度有所增加，水平剪切阶段的刚度略有差异，斜面压剪阶段的刚度随厚度增加而减小。这与理论模型中的影响趋势相符。

图8(b)给出了橡胶层厚度对支座试件等效刚度、阻尼比的影响。从图中可看到：1)随着厚度增加，支座试件的等效刚度减小；2)厚度增加，支座试件的阻尼比增加。由上可得，相同位移下选用较大厚度有利于支座充分发挥作用。

2.2.4 加载位移相关性

图7(c)给出了在竖向压应力为4 MPa时不同加载位移时，坡度角为45°、橡胶层厚度为10 mm的试件的影响。通过比较不同位移下支座的耗能能力，考察支座的变形性能。

从图中可以看出水平加载位移对试件耗能性能影响显著，加载位移在5 mm时所围成滞回环曲线的面积较小；加载位移翻2倍至10 mm时滞回环曲线围成的面积增加倍数超过2。

图8(c)给出了加载位移对支座试件等效刚度、阻尼比的影响。从图中可知：1)水平加载位移增加，支座试件的等效刚度先增加后减小；2)水平加载位移增加，支座试件阻尼比逐渐减小。

2.2.5 竖向压应力相关性

图7(d)给出了坡度角为 45°，水平加载位移为8 mm，不同竖向压应力情况下，支座所形成的力-位移滞回曲线。

由图可知，在加载位移相同时，随着竖向压应力的增加，所围成滞回环整体形状变得更加尖锐，即斜面压剪阶段的尖角更为显著。不同压应力下的最大摩擦力增加比例与应力增加比例不同，因为橡胶层与盖板之间的摩擦系数随着竖向压应力变化[21]。

图8(d)给出竖向压应力对隔震支座等效刚度、阻尼比的影响。从图中可以看出：1)竖向压应力的增加，隔震支座等效刚度增大；2)竖向压应力的增加，支座试件阻尼比先增后减。由上可得，竖向压应力对支座耗能表现有一定影响。

表3为不同设计参数试件的等效刚度及阻尼比。

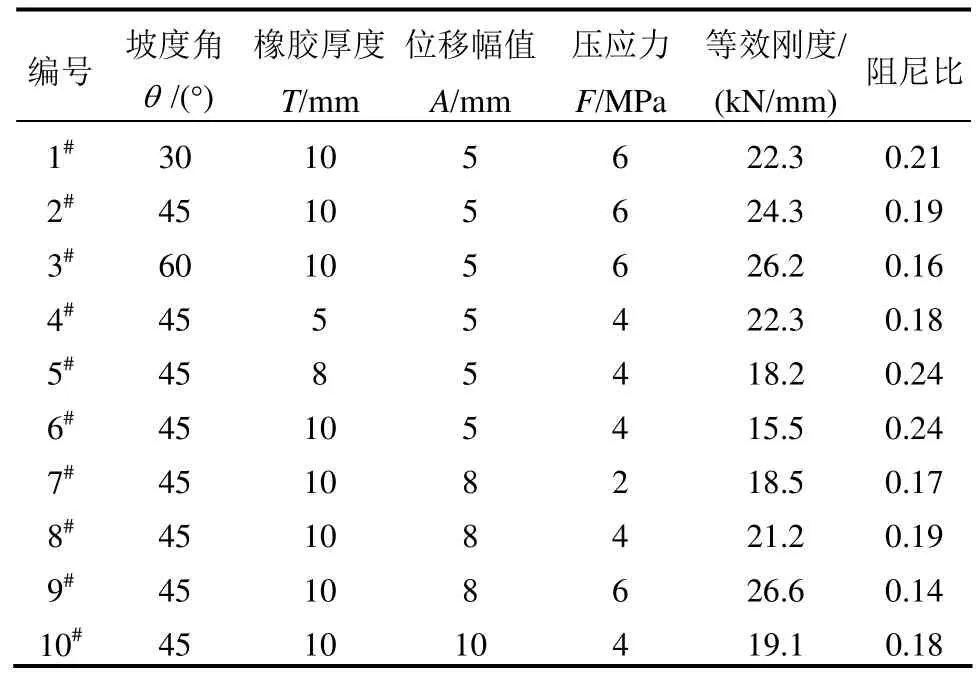
表3 支座试件等效刚度及阻尼比实验值Table 3 Effective stiffness and damping ratio value of test specimens

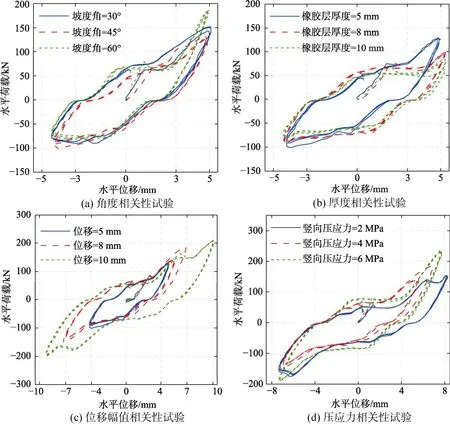
图7 试验滞回曲线图Fig.7 Hysteresis curve of static test

图8 试验等效刚度与等效阻尼图Fig.8 Effective stiffness and damping ratio diagram of static test

3 锥形支座地震响应分析

3.1 锥形支座高宽比限值

由于锥形非固结支座不承受拉力，在地震作用时结构存在提离甚至倾覆的可能，将结构边角支座即将处于零应力状态作为临界条件的判别依据。以此对支座适用结构高宽比进行限定。

考虑上部结构水平地震作用可得：

结构提离力矩：

抗提离力矩：

式中：mi是结构第i层的质量；分别为结构第i层相对支座的加速度和位移；为地面运动水平加速度；hi为结构第i层楼的高度；B为结构基础底部宽度，见图9。

支座在即将脱离时，上部结构的抗提离力矩与提离力矩有如下关系：

图9 倾覆计算示意图Fig.9 Overturning calculation diagram

将式(6)和式(7)代入式(8)可得到结构不发生倾覆的基础最小宽度式(9)：

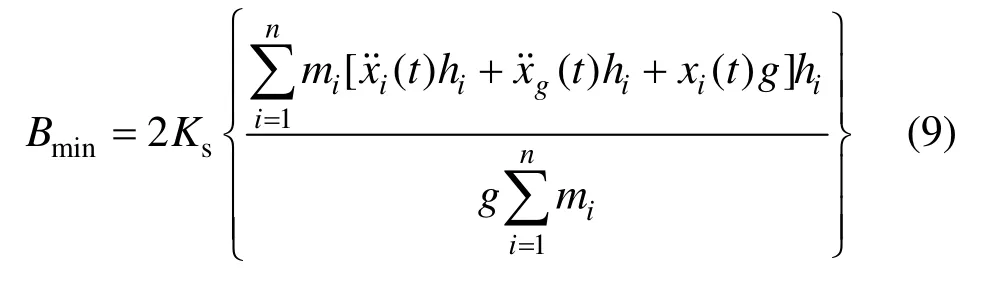
考虑到非固结的特点，对于计算得到的最小宽度设安全系数Ks取1.5。对于不同的场地取对应特征周期，在计算模型中调整结构高度，由式(9)计算得到基础最小宽度。表4给出了在各类地震作用下，不同场地的高宽比限制。

表4 地震作用下不同场地高宽比限值Table 4 Aspect ratio limits of different sites under seismic effect

由表4可知，对于建在硬场地上的房屋，支座的高宽比限值明显大于软弱场地的值，可见锥形非固结支座更适合在Ⅰ类、Ⅱ类场地条件上使用。

3.2 算例分析

为进一步研究锥形非固结隔震结构高宽比限值和支座参数对地震响应的影响，采用有限元软件对锥形非固结隔震结构进行分析，支座的本构模型之前所示，抗震设防烈度为8度，基本设计加速度为0.2g，场地类别为Ⅲ类。分别进行高宽比为0.65、2、4的计算分析。上部结构标准层和隔震层布置分别如图10、图11所示。其结构动力特性第1阶周期按0.09N~0.13N(N为上部结构层数)。

支座参数对地震响应的影响则通过改变影响支座水平刚度的关键因素，分析在地震作用下隔震结构响应规律，并与非隔震结构的地震响应结果进行比较。锥形支座由于其构造，适用于高宽比较小的结构，故选用高宽比为0.65的模型。所选用力学参数及对应位移见表5。模型结构总质量743 t，底层层高 3.3 m，标准层高 3 m，地面以上总高为9.3 m，支座各个因素的力学参数如表5所示。由第1节的理论模型可得，影响锥形支座力学性能的关键因素为橡胶层厚度和坡度倾角，通过调整这两个因素，该结构隔震周期为0.83 s ~1.02 s。

选用2条天然波(Landers,Cape)和1条人工波(RH1)进行地震动分析。按照 8度设防水准进行加载(对应峰值加速度为0.2g)。X方向与Y方向的输入峰值之比为1∶1。

3.3 高宽比限值及地震响应结果分析

图12(a)~图12(c)为不同高宽比下，隔震结构顶层的地震响应。由图可得，随着高宽比的增加，顶层的响应在随之增加。在高宽比为4时，顶层加速度已有放大，层间位移已经超过限定值 1/550[22]。从图12(d)可得，在高宽比超过当前烈度限值2.1时，倾覆力矩已超过抗倾覆力矩。

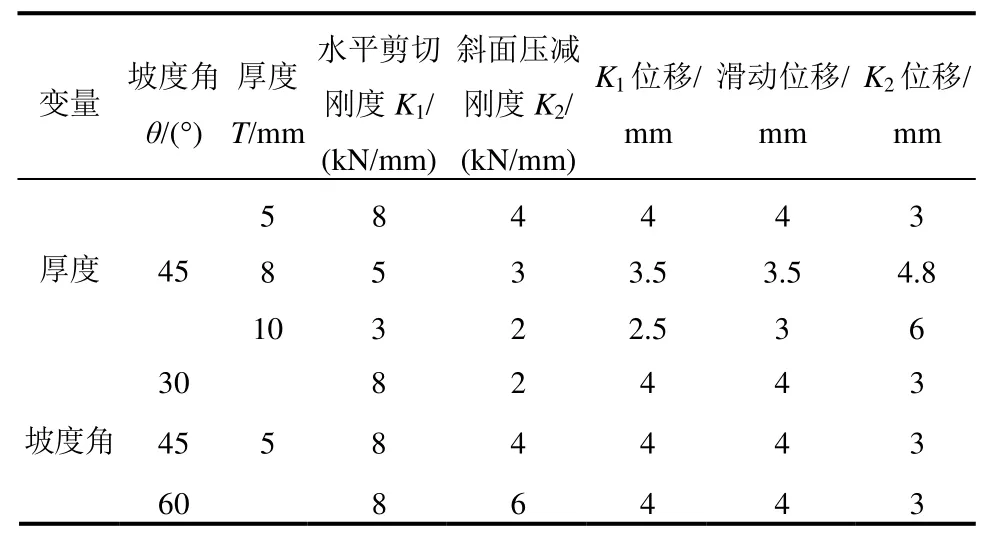
表5 选定高宽比下力学参数组合Table 5 Mechanical parameter combination for selected aspect ratio

图10 上部结构标准层Fig.10 Superstructure standard layer

图11 支座布置图Fig.11 Layout of bearing

图13给出了在橡胶层厚度改变的情况下，地震响应的变化。篇幅的限制，仅列出3条地震波Y向的响应平均值，及5 mm这组参数下的滞回曲线。可以看出，隔震效果明显，且效果随着厚度增加而提高。3组参数都使结构顶层加速度降低60%以上；隔震之后最大层间位移为 1/589，在许可范围内；层间剪力最少降低45%。5 mm所形成的滞回曲线饱满，说明耗能良好。

橡胶层厚度直接影响两个阶段刚度，不同厚度之间区别明显。对于结构顶层加速度，10 mm的效果比5 mm提高27%；结构顶层层间位移10 mm比5 mm提高23%；结构顶层层间剪力10 mm比5 mm提高24%。说明相同面压的情况下，锥形支座的橡胶层应选择较厚的组合。

图12 高宽比对结构响应影响Fig.12 Effect of aspect ratio on structural response

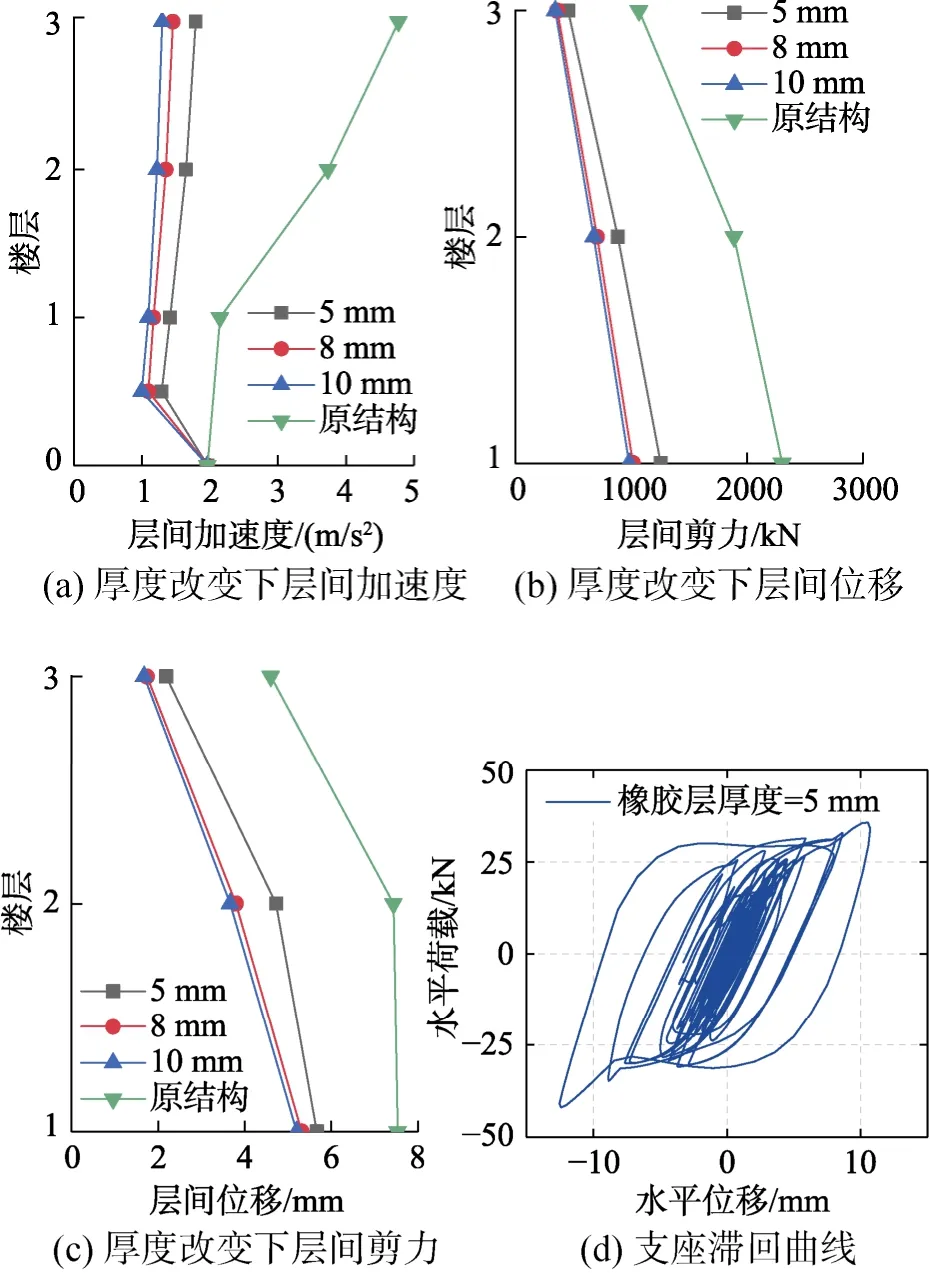
图13 地震响应与厚度相关性Fig.13 Correlation of seismic response and thickness

图14为不同坡度角的地震响应。滞回曲线仅列出60°这组。由图可知，3组不同参数的隔震效果明显。结构顶层加速度降低60%以上；隔震之后最大层间位移为 1/578，在许可范围内；层间剪力最少降低 44%。60°所形成的滞回曲线饱满，压剪阶段现象更为凸出。

由理论公式可得，坡度角仅影响斜面压剪阶段的刚度，即对支座的临界值有显著影响。结构顶层加速度差异较大，60°比30°减震率减小了11%。结构顶层层间位移和剪力差距较小，60°比30°减震效果均减少了 2%。说明相同面压的情况下，应尽量选用坡度角较小的锥形支座。

图14 地震响应与坡度角相关性Fig.14 Correlation of seismic response and slope angle

4 结论

本文通过静力试验验证所构建的锥形支座理论模型，探讨了影响支座力学性能的因素，并建立了含锥形支座的隔震结构并进行地震时程分析，结论如下：

(1)锥形支座的运动状态主要分为水平剪切、滑动摩擦及斜面压剪3个阶段。提出了水平刚度的计算公式并构建了理论力-位移的曲线。

(2)静力试验结果分析表明所提出的理论模型与实际状态吻合较好。影响性能的因素分析中，坡度角越小，支座所形成的滞回环面积和斜面压剪阶段刚度越大；橡胶层厚度越大，支座所形成的滞回环面积略增加，两阶段水平刚度均明显减小；加载位移越大，支座所形成的滞回环越饱满，越有利于耗能。

(3)高宽比限值的分析可得锥形非固结支座更适合在Ⅰ类、Ⅱ类场地条件上使用。Ⅰ类、Ⅱ类、Ⅲ类和Ⅳ类场地的最小高宽比分别为2.3、1.7、1.3和 0.5。在随着高宽比的增加，顶层的结构响应增加。通过数值模拟可得，锥形支座的隔震模型均能有效减小结构在地震作用下的响应。加速度响应最少减小60%，剪力响应最少减小45%，位移响应均在规范容许范围内。橡胶层越厚，隔震效果越显著；坡度倾角改变对隔震效果影响不明显，对压剪阶段的极值影响更大。

锥形支座构造简单，有利于施工，且有良好的耗能效果，可有效解决广大高烈度底层及多层房屋的抗震问题。在设计时应采用厚度较大，且坡度倾角较小的组合以充分发挥耗能能力。