基于力流等效的环形网顶破力学行为解析方法
2020-04-18郭立平余志祥骆丽茹赵世春
郭立平,余志祥,2,骆丽茹,齐 欣,2,赵世春,2
(1.西南交通大学土木工程学院,成都 610031;2.陆地交通地质灾害防治技术国家工程实验室,成都 611756)
崩塌落石、山体滑坡、泥石流、雪崩等环境灾害广泛分布于世界各地(加拿大[1],欧洲[2],中国[3-6],美国[7]和印度[8]等),柔性防护系统作为常用的防灾手段,发挥着重要的安全防护作用[9]。柔性防护网结构是一种复杂的非线性结构系统[10],由柔性网、支撑构件、耗能器[11-12]、高强钢绳等部件组成,其中,柔性网是柔性防护系统的关键受力部件,承受落石的顶压作用并进行拦截[13-14]。目前,柔性防护系统常用菱形网、双绞六边形网、G.T.S网和环形网等作为拦截单元(图1)。柔性网一般呈“松散”连接[15],遭受冲击时,往往伴随强烈的接触、滑移和损伤等非线性特征,致使柔性防护系统的设计变得非常复杂,工程应用容易出现损毁风险[16-18]。

图1 网片类型Fig.1 Types of different net panels
柔性防护系统主要遭受冲击作用,网片的大变形是防护系统缓冲能力的重要保证[19]。Tan等[20]研究发现,与刚性结构相比,相同冲击能量下,柔性网的大变形使冲击作用持时延长了4倍~8倍,冲击力降幅达 50%以上。Yu等[21]研究发现,在被动柔性防护系统中,环形网的冲击变形受钢丝股数、边界约束影响,但变形量相对稳定,约占系统变形的30%~40%等[22]。Buzzi等[23]发现,移除加劲绳可降低防护系统刚度,更有利于柔性网片大变形,可进一步降低钢柱与支撑绳的内力。
网片还是重要的承载与拦截部件。Buzzi等[23]研究发现,在冲击能量较低时(35kJ),菱形网片自身耗散了大部分的冲击能量。Bertrand等[24-25]进行了2 m×2 m尺寸G.T.S网片试件的准静态顶压试验,发现网片顶破极限承载力与顶头接触面积大小(代表落石与网片的接触尺寸)密切相关。Spadari等[26]和 Mentani等[27]开展了量纲分析及模型试验,研究了菱形网片、双绞六边形网片低冲击能量作用下的“子弹效应”,发现即使冲击能量较低,由于顶压接触面积较小,网片的破坏现象依然突出。Castro-Fresno等[28]对菱形网片分别进行了集中力与分布力加载试验,研究了钢丝网片的承载力与变形特征,发现与集中力加载相比,分布力加载时网片的极限变形减小,极限承载力增加至2倍以上。Koo等[29]采用LS-DYNA比较了球体与平板对柔性网片的冲击动力响应,发现平板冲击时,变形量显著降低。柔性防护系统的灾害作用包括单个落石冲击、碎屑体冲击、滑坡、雪崩、泥石流等,冲击作用的分布区域涵盖局部单点至整个拦截网面,这使得防护系统的力学行为变得非常复杂,但就网片部件的承载而言,局部冲击导致的顶破作用是更为不利的。
鉴于柔性网受力的复杂性,很多学者对其力学模型与分析方法展开了研究,但多针对相对简单的菱形网[30]。实际工程中,环形网因其大变形和高承载力获得广泛使用。环形网一般由高强钢丝缠绕不同圈数形成的网环套结制成,钢丝圈数、网环直径是环形网片的重要参数。如图2所示,其中钢丝圈数表示为nw(图中nw=7),单环直径为d。

图2 单环规格Fig.2 Specification of steel wire ring
由于单元间的接触滑移影响,环形网力学行为更加复杂,这引起了学者们的关注,如 Escallón等[31]采用离散梁单元,考虑接触、滑移、损伤等非线性因素,构建了离散化冲击力学模型,并通过1000 kJ冲击试验进行了验证。这种方法计算精度很高,但参数繁多,加之建模复杂,影响了其适用性,为此,学者们对简化计算方法开展了研究。Gentilini等[10]将环网简化为Truss单元模型,提高了计算效率,降低了分析难度,但由于将网环间的滑移边界简化为铰接约束,使得网面刚度增大,计算得到的承载力大大高于实际值。
上述研究对揭示柔性防护系统复杂的非线性力学行为起到了推动作用,但对受力传力最为复杂的柔性网片单元的研究是不充分的,大多研究仅仅将柔性网单元简化为冲击作用的传力单元,忽视了网片单元自身的受力破坏特征,而这种破坏恰恰是实际较为常见的现象[17]。为此,本文研究了考虑环形网主要受力破坏特征的解析力学方法,通过8组共 24张环形网片的拟静态顶破试验,考虑网环圈数、网环直径、顶压区尺寸、传力路径、破坏特征等多因素影响,建立了环形网解析分析方法,并结合试验结果论证了方法的准确性。
1 顶破试验
1.1 试验方法
参考瑞士标准[32],柔性网片顶破试验采用自行研制的顶压试验装置(图3)沿网片表面法向施加顶压荷载,试件采用工程中的常用规格网片,共8种,网环圈数nw=3,nw=4,nw=5,nw=7,nw=9,nw=12,nw=16,nw=19。为保证试验数据的可靠性,每种规格进行3次破坏性试验。顶破试验设备的组成为:1)反力架基座梁,用于约束柔性网片试件;2)卸扣,连接于反力架基座梁上,对称布置,用于连接网片;3)环形网片,高强钢丝编制成环,由若干网环相互套接成形;4)球冠形加载顶头,连接在铰接板端部,用于对网片传递顶压作用;5)板式铰接销,连接顶头与传感器;6)拉力传感器,根据网片规格选用,有500 kN、1000 kN及1500 kN三种规格,精度为 0.3%;7)拉线式位移传感器,测试并记录位移行程,量程>1.5 m,精度0.3%。位移与拉力量测值通过数据采集系统实现同步;8)反力架,内部空间 3.15 m ×3.15 m;9)液压作动器,位移行程2.5 m;10)数据采集系统。

图3 顶破试验装置Fig.3 Apparatus of punching test
加载时,顶头预置于网面下,经由液压作动器提供竖直向上准静态位移,顶头缓慢提升后与网面发生接触。该过程中当加载顶头底面与网面等高时,认为试件初始松弛量被消除,此状态作为标定初始状态。作动器的位移加载速率为7 mm/min。当拉力测试值出现峰值并极速下降时,停止加载。摄像机记录顶破试验过程,数据采集系统记录环形网加载历程的顶压力、顶压位移。
1.2 试验模型
试件采用环形网片为正方形,网片尺寸如图4所示。网片边长理论值w由式(1)计算。其中,d为单个网环内径,本文试件均取d=300 mm;ns为环形网片边缘的单环个数,本文均取ns=7。

试件参数见表1,以规格 R07/3.0/300网环为例说明:R07表示网环的钢丝缠绕圈数nw=7,3.0代表组成网环的钢丝直径为dmin=3.0 mm,300表示单环内径为d=300 mm。

图4 试件规格Fig.4 Parameters of specimen
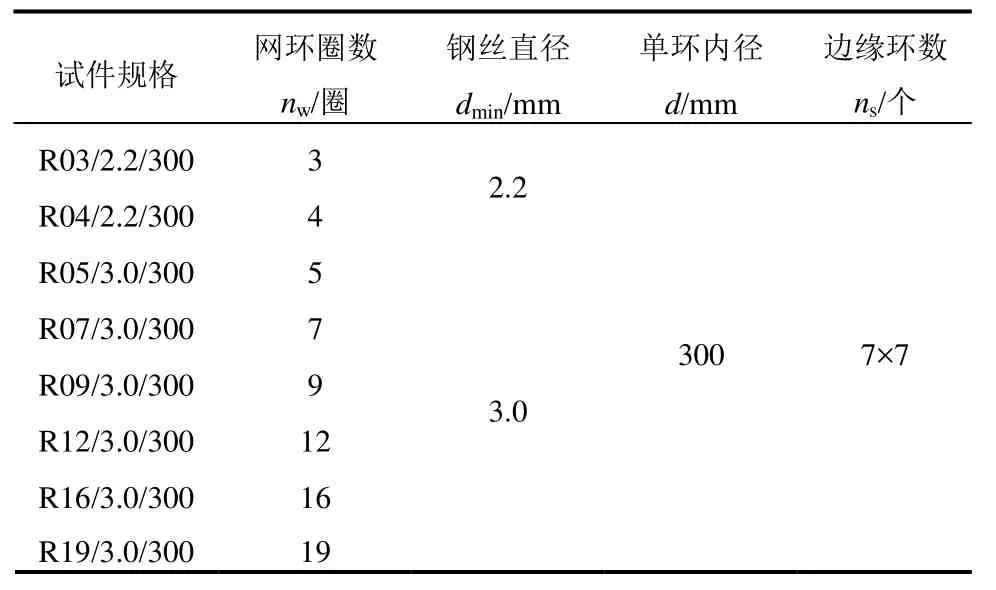
表1 试验试件Table 1 Specimen of tests
球冠形加载顶头置于网面中心,球面半径为Rs=1.2 m,球冠底部切面为圆形,在水平面投影半径Rp=0.5 m。球冠包角为2β0,β0由式(2)计算。

1.3 试验结果
如图5所示,试件加载变形过程分别经历了初始状态(状态I)、拉弯分界状态(状态II)和顶破极限状态(状态III)。图5中与顶头接触的网面定义为顶压区域Ac,其余网面为传力区域At。
初始状态(状态I)网环呈圆形,可近似认为处于零应力状态。从状态I到状态II,随着顶头提升,网环由弧形逐渐拉直,主要经历弯曲变形。仔细观察影像记录,还发现网环拉弯变形的发展有先后顺序,主要表现为:沿顶头圆周到基座梁垂线方向的网环最先被拉直,并扩展至网面的对角区域(图5)。拉弯分界状态(状态 II)为网环变形模式从弯曲变形转变为轴向拉伸的分界。状态II时,网环弯曲变形充分发展,几乎都呈拉直的钢丝束纤维[33](以下简称纤维),此刻加载顶头提升位移记为h。由于约束差异,此时网环变形分别表现为“△”形、“口”形和“ ”形,分别分布于试件底部约束边缘、顶压接触区域Ac和传力区域At。状态II以后,网片试件的形状变化不明显,但试件整体的漏斗状变形进一步发展,与实际工程中网面遭受落石冲击时的变形非常相似[17]。顶破极限状态(状态III)时,加载顶头边缘位置的网环钢丝率先发生破断,形成“破断豁口”(图6),此时停止加载,试验终止。8种规格共 24张环形网片试件均表现出一致的破坏模式(图6),表明位于顶头环周边缘的网环单元是拉力传递的关键部位。
观察状态II和状态III(图5)可知,网面传力区域At沿着网面径向形成了若干道呈辐射分布的三角形环链,环链内的网环呈渐变“ ”形,环链底端与加载基座梁相连的网环为“△”形,环链顶端与顶头接触区域的网环为近似“口”形。沿顶头圆周到基座梁垂线为最短传力路径,根据力流分析[34],可知该路径上的环链受力最大。同时,状态III时沿顶头径向,网片拉直形成了辐射状纤维,这表明网片主要承担辐射向拉力作用,这为借助力流分析方法对环网顶破极限状态进行解析提供了途径。
图7为试件顶压加载历程的力-位移关系。环形网片试件的制造误差、钢绳卡扣的压紧程度、网环之间套结位置的差异均会对试验过程顶破力、顶破位移的测试结果造成影响,为此,每组试验采用包含相同规格网片的3次重复试验。尽管如此,从试验结果来看,3次重复试验结果仍呈现较大离散性,统计相对误差最大约20%。据图7可知,力-位移关系表现出明显的两阶段特征:第1阶段(状态I至状态II),大部分网环发生弯-拉变形,拉力增幅缓慢(约占顶破力10%~20%)、变形增幅明显(约占总变形量80%~90%);进入第2阶段(状态II至状态III),变形小幅增加(约占总变形量10%~20%),拉力迅速增大(约占顶破力 80%~90%)。直至顶头提升高度为h+Δh时,拉力达到峰值,顶头环周边缘网环发生破断,到达顶破极限状态。图7中采用竖直分界线近似标记了总变形量 85%位置近似为拉弯分界状态,红线左侧即为第1阶段,右侧为第2阶段。

图5 环形网片顶破试验与过程Fig.5 Puncture tests of ring net panels and deformation mechanics

图6 破断豁口位置Fig.6 Failure position of ring net

图7 不同圈数环形网片顶破力-位移曲线Fig.7 Out-of-plane force-displacement curve of different steel ring net panels
2 环网顶破承载解析力学模型
2.1 模型假设
1)假定拉弯分界状态网片环绕加载顶头方向(环向)和顶头半径方向(径向)纤维受力具有正交性,忽略环向的纤维影响,第2阶段网片受拉承载为连接Ac与At区域直线纤维内力矢量之和,顶头边缘纤维的数量即为力矢量的个数(图8)。
2)假设环网破坏由环链轴向应力发展程度γN决定,一旦应力最大的纤维轴向应力发展程度到达极值γN时,网片发生破坏。

式中:σ为当前轴向应力值;σy为轴拉屈服时的轴向应力值。
3)忽略环形网片重力影响。

图8 第2阶段受力纤维假定Fig.8 Straight line fiber
2.2 顶压区受力分析
根据假定,拉弯分界状态顶压区网环纤维与加载顶头发生接触作用。选取绕过顶头的纤维中间段作为研究对象(其余分段可视为中间段的延伸),受力分析如图9所示。

图9 顶压区网环受力分析Fig.9 Force analysis on contact area
沿纤维方向两端受到拉力作用Ts、Tr,与纤维方向垂直的拉力Ti、Tj、Tk、Tl,沿球面法向的正压力 dN,沿纤维方向的摩擦力μtdN,垂直于纤维方向的摩擦力μrdN。结合试验现象,第1阶段(状态I至状态II),环形网片面外变形迅速发展,在上述接触摩擦作用下环形网片变形扩展并沿顶头表面滑动,第2阶段(状态II至状态III),环形网片顶压区纤维段不再沿拉力垂直方向发生明显滑动,认为此时主要承受沿纤维走向轴向拉力Ts、Tr、沿球面法向的正压力集度 dN、沿纤维长度方向的摩擦力μtdN,因此可将该区域网片的受力进一步简化为二维模型(图10)。图中T1和T2分别为顶压区左右侧纤维的拉力合力,由对称性T1=T2,β0为1/2顶头的球面包角。取任意角度β处(β≤β0)的一个纤维微段分析,微端包角为dβ,β处拉力值为T,β+dβ处拉力值增大至T+dT,沿微段长度Rsdβ上受到的法向接触力为dN,切向摩擦力为μdN(μ=μt)为纤维与刚性顶压区域之间的摩擦力)。

图10 顶压区域受力纤维Fig.10 2-D computational model of loading area
对纤维微段受力进行正交分解,法向η轴、切向ξ轴平衡方程如式(4):

忽略高阶无穷小量dTdβ,由式(4)得:

进一步整理得式(6):

在β=0~β0区间内两边积分,得式(7):

式中,T(β)为任意角度β位置处纤维的轴向拉力(图11)。T0为β=β0位置处纤维轴向拉力。随着β的增大,T(β)不断增大,当β=β0时,纤维轴向拉力达到最大(式(8)):

可知环形网片顶压区域Ac边缘纤维拉力最大,是网片的薄弱区域,这也与试验现象(图6)一致。

图11 顶压区域纤维轴力分布Fig.11 2-D computational model of loading area
2.3 传力区环链受力分析
第2阶段受力时,网片试件沿最短传力路径上的网环在三角形轮廓内由若干个“ ”形网环串联形成环链,如图12所示。图10(b)中,O点为网片的几何中心;ai表示三角形环链沿斜边轮廓上的分段长度;li为环链沿最短传力路径方向上的空间斜长;bi为相应垂直方向的分段长度(i=1,2,3…n);n为最短传力路径上区格分段,对特定环形网片,边缘单环个数为ns(图4),则n=ns–1;θ为最短传力路径上三角形轮廓1/2最小内角;根据假定,第2阶段轴向力尚未发展,即网环轴向应变为零,拉弯分界状态三角形环链中各区格周长应相等,据此可建立求解θ的方程组(式(9)):

图12 环形网片拉弯分界状态变形特征(阶段1: z=h)Fig.12 Feature triangle in ring net panel (Stage 1: z=h)
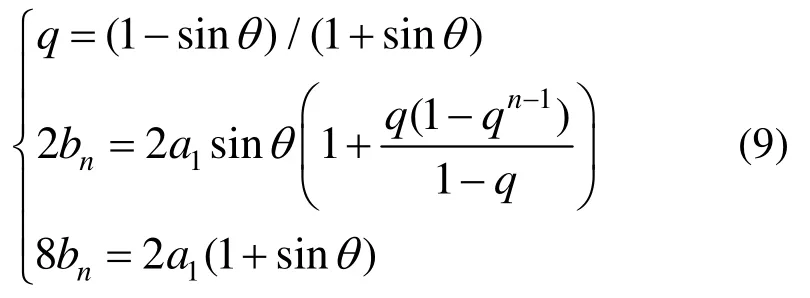
式中,q为中间变量,由于θ>0,q≠1,经化简整理得:

通过式(10)解得θ,结合图12(b),进一步得到lsum:

2.4 应力特征分析
顶破极限状态下环形网片特征位置的应力分布特征及发展程度对顶破力、顶破位移计算有重要影响。鉴于拟静态顶破试验过程中各个网环均经历非线性变形,从文献[35-36]来看,目前尚无有效手段直接测试网环内的钢丝(直径2.2 mm~3.0 mm)的应力-应变。为考虑顶破极限状态网环内轴向应力分布及发展程度,借鉴已经试验验证的环形网片有限元模拟方法[16,37],以R7/300/3.0规格为例,分析了最短传力路径的应力分布特征(图13)。
如图13所示,最短传力路径上网环有效应力明显发展,网片破断豁口出现在加载顶头边缘,与试验结果一致。选取了最短传力路径上接近顶压区网环的8个特征点(P1-1~P4-2),统计了截面轴力、弯矩、轴向应力、轴向应变及轴向应力发展程度(表2)。表2可以看出,趋于顶破极限时,尽管网环套结位置由于拉弯组合作用最先进入屈服并发生破坏,拉直段网环以轴拉为主,截面轴力值为29 kN~35 kN,轴向应力小于弹性极限606 MPa~701 MPa,轴向应力发展程度λN与环链试验结果[37]一致 0.36~0.40,弯矩值处于 19.5 N·m~24.0 N·m。轴向应力发展程度决定了顶破力的大小,环绕顶压区边缘拉直的网环内力矢量之和在竖直方向的分量形成了面外顶破力。通过环链试验[37],可以更为直接地测得套接网环发生破坏时的轴向应力发展程度,图14给出了环链试验、FEM模型获得的轴向力发展程度结果,可见有限元(FEM)应力分析结果与环链试验结果一致,通过线性拟合(拟合优度0.8525)得γN的参考值为:

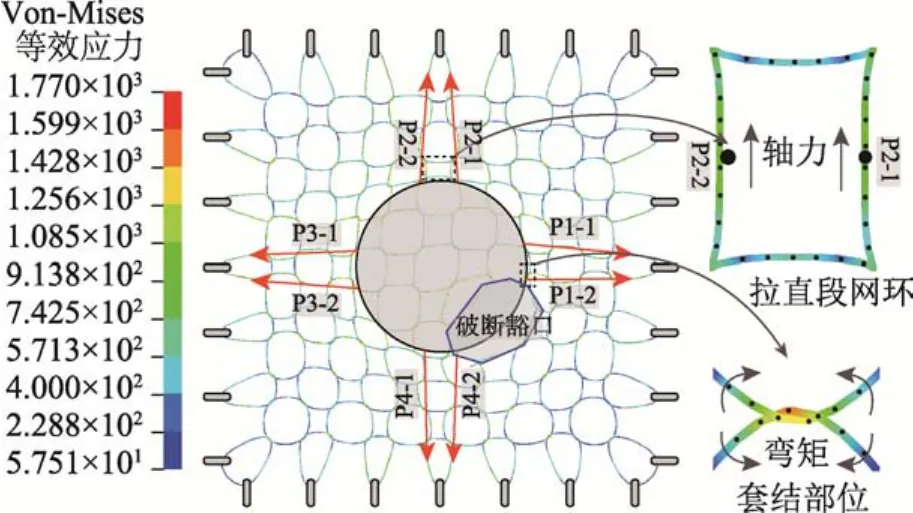
图13 顶压区网片应力特征Fig.13 Stress feature of the net panel in contact area

图14 轴向力发展程度参考取值γNFig.14 Axial force factor (γN)in ring chains

表2 环形网片特征位置应力分布Table 2 Stress distribution of the feature points on the net panel
2.5 计算模型
选用笛卡尔坐标系(xyz)作为计算模型的基准坐标系。以试件拉弯分界状态(状态 II)建立环形网片的计算模型如图15所示,图15(a)为模型俯视图,图15(b)为主视图、左视图,L为顶压区域边缘与约束边界间的最小距离;h为加载顶头的边缘提升高度,其余符号含义同前。
当试件处于拉弯临界状态时,顶头接触区域内的网环变形至近似正方形,其边长为:
传力区域由网环拉直形成的纤维与顶压区边缘的交点编号为u[1],u[2]…u[i]…u[m],与之对应,边界(z=0)处约束点编号为d[1],d[2]…d[i]…d[m],m表示1/8模型中最大交点个数(图15(a)红色纤维),m可由式(14)计算。
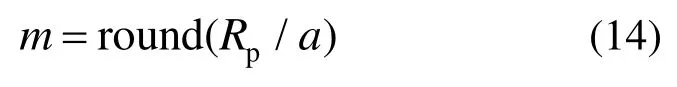
式中,round为取整函数。
结合2.3节分析结果,通过式(11)得到lsum,由图15(b)可进一步得到L关于lsum的表达式:

由于钢丝圈数及钢丝直径对套接位置处网环的曲率影响对于L的计算不可忽略,因此式(15)中引入函数f(nw,dmin)近似估算其影响值,并取f(nw,dmin)=nwdmin。据此可进一步得到拉弯分界状态加载顶头上升高度如式:

通过上述分析,拉弯分界状态顶压区域(1/8模型)边缘上部连接各点坐标可表示为:

其中,i=1,2,…m。传力区域下部各约束点位置均匀分布,其坐标为:

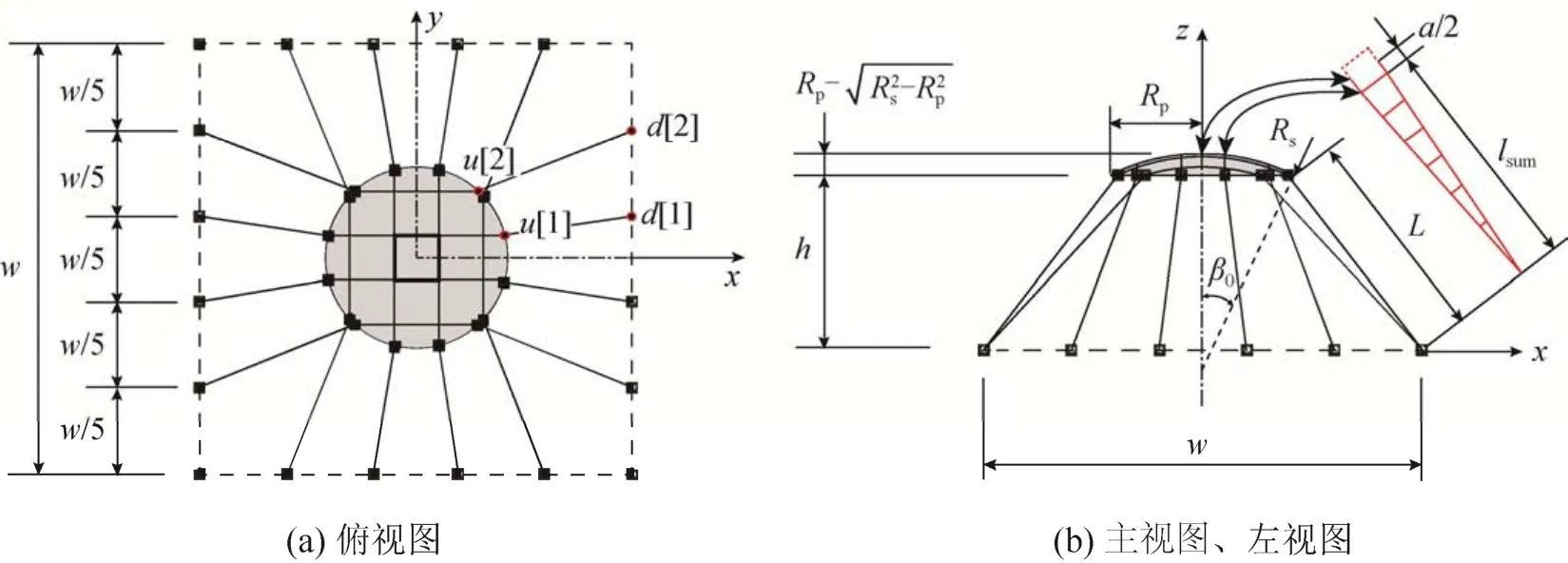
图15 模型尺寸(拉弯分界状态)Fig.15 Geometric parameters of analytical model
记状态II(z=h)时刻,任一纤维的长度为d[i],用向量表示第i个纤维在xyz坐标系中的相对位置如:

则状态III(z=h+Δh)时刻,第i个纤维可由向量表示为:

其中,Δh为待求量(图5),第i个环向分布纤维产生的轴向应变为:
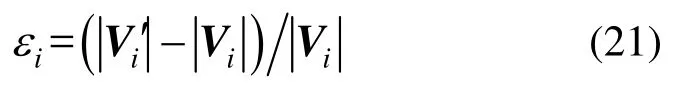
为确定最大轴向应变对应的i值,将式(21)对i求偏导:

其中:


纤维的失效应变εf由轴向力发展程度γN确定,可由式(24)计算:

其中,γN由式(12)计算。
联立式(17)~式(24),得到状态II至状态III过程中环形网片面外变形增量Δh:

由此确定了式(20)中的未知参数Δh。此时,顶破极限状态(z=h+Δh)下沿环向分布的第i个纤维力矢量可表示为式(26):

为方便表示,引出标量Ci:

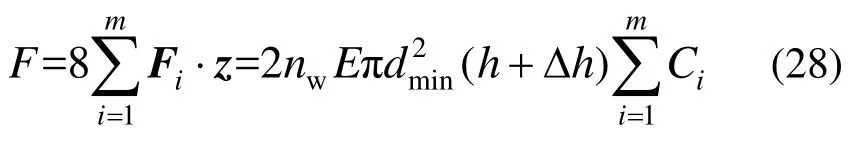
顶破极限状态(z=h+Δh)顶破位移计算:

3 算例验证
基于本文提出的计算方法,编制了用于求解不同规格环形网片承载力及变形的python程序,计算流程如图16所示。顶破力、顶破位移计算结果与试验结果对比如表3所示,其中,为不同3次试验顶破力平均值,Fm为本文模型顶破力计算值,δ(F)为顶破力计算与试验结果相对误差。同样,为3次试验顶破位移平均值,Sm为模型顶破力值的计算结果,δ(S)为顶破位移计算与试验结果相对误差。表中顶破力与顶破位移计算结果与试验结果相对误差均在15%以下,对比其他柔性网相关文献,计算结果相对误差可达5%~40%(Grassl[38]的数值模型误差为6.06%~19.23%,Cui等[39]的解析模型误差为14.2%~16.5%,Hambleton等[34]的解析模型误差为10%~40%)。由于环形网片制造、安装过程存在误差、试验结果离散性较大,进一步提高柔性网片的计算精度具有较大难度,作为系统选型与设计用途,认为目前的精度可满足工程需求。

表3 顶破力、顶破位移计算结果与试验结果对比Table 3 Comparison between the calculation results and test results of maximum force and deflection
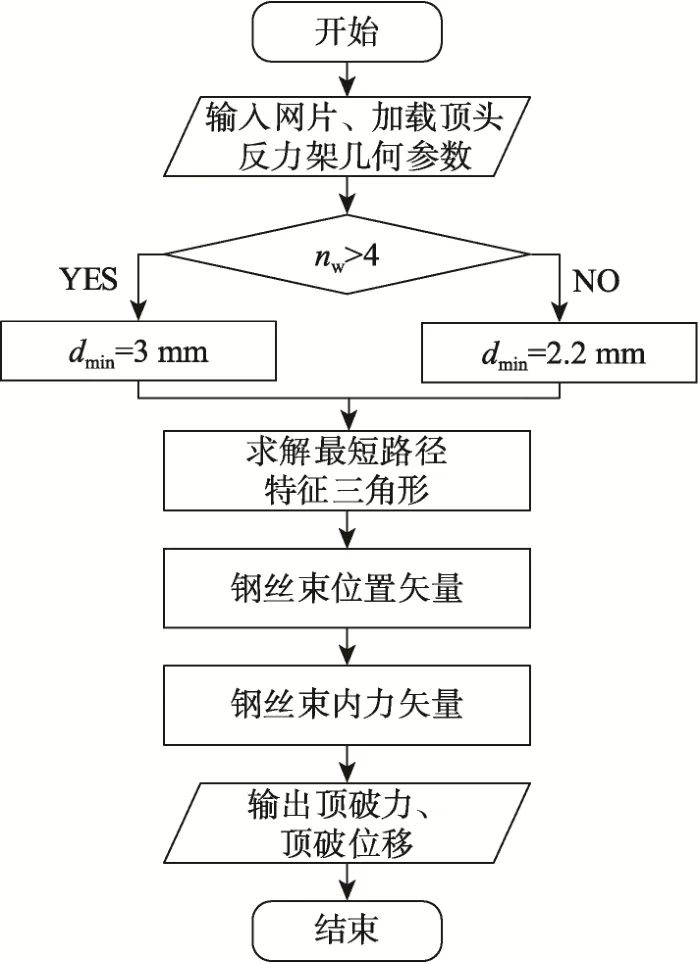
图16 计算流程Fig.16 Calculation flow chart of the model
4 结论
(1)网片遭受顶破作用时,主要遭受加载顶头的顶压作用与传力区的拉力作用,24张环形网片拟静态顶破试验均表现出相似的破坏模式,顶压区域边缘位置是环形网片最先破坏的薄弱环节。网环圈数、网环直径、顶压区尺寸为影响环形网片承载能力、变形能力的关键因素。
(2)根据试验结果开展了力流分析,建立了环形网片顶破力学行为的解析计算方法,推导了考虑圈数、顶压区尺寸、网环直径影响下的顶破力、顶破位移计算公式,计算结果与试验结果相对误差小于15%,验证了该方法的可靠性,可为柔性防护结构方案中环形网片的选型与设计提供参考。
限于试验条件,模型并未考虑环形网片长宽比、边界条件变化等不同的情形,需要进一步开展研究。
