箍筋约束混凝土圆柱轴压强度尺寸效应律

金 浏，李 平，杜修力，李 冬,2

(1.北京工业大学城市减灾与防灾防护教育部重点实验室，北京 100124；2.清华大学土木工程系，北京 100084)

约束混凝土通过约束来限制混凝土横向变形的发展，从而增强混凝土构件的强度与延性。目前混凝土柱中采用多种工程材料提供横向约束，包括钢材(箍筋[1]及钢管[2]等)及多种纤维增强材料(如：碳纤维[3]、钢纤维[4]及玻璃纤维[5])等。其中，箍筋约束是混凝土结构中最简单常见的一种约束方式。

从1903年Considere第1个提出螺旋箍筋可以提高混凝土的强度，对箍筋约束混凝土的研究至今已有一百余年。国内外研究者开展了大量的试验及理论研究，对箍筋约束作用的力学特性进行深入的分析，并提出了多种约束混凝土应力-应变关系模型。1988年Mander[6]等提出了考虑箍筋形式、间距及体积配箍率等多种因素影响的约束混凝土力学模型，该模型力学机理清晰，得到广泛应用。此外，Kent和 Park[7]，Sheikh和 Uzumeri[8]、Legeron和Paultre[9]、过镇海等[10]及史庆轩等[11]均提出了各自的箍筋约束混凝土理论计算模型。在较小尺寸范围内，上述理论方法的计算结果与试验实测值吻合良好。

现存的许多文献[12-14]均证实了箍筋约束混凝土柱轴心受压强度存在明显的尺寸效应，且其尺寸效应随约束作用的增强而减弱。另外，Kim等[15]试验结果表明：箍筋约束混凝土柱轴压破坏尺寸效应的强弱受体积配箍率的影响，即随着体积配箍率的增加而逐渐减弱，当体积配箍率达到某一临界值时，混凝土尺寸效应将消失。然而，目前关于箍筋约束混凝土柱承载力计算理论大多未考虑尺寸效应的影响。此外，我国《混凝土结构设计规范》[16]也未考虑尺寸效应对钢筋混凝土柱轴压承载力的影响。

钢筋混凝土构件层次尺寸效应主要源于两个方面[17-18]：1)混凝土材料自身的非均质性；2)钢筋与混凝土间复杂的非线性相互作用。现有尺寸效应理论，包括 Bažant基于断裂力学的尺寸效应理论[19]、基于多重分形的 Carpinteri尺寸效应理论[20]、及 Weibull随机强度统计理论[21]等，均是针对混凝土类脆性材料，采用理论推导及半理论半经验等手段建立起来的理论公式。目前，大量的试验研究工作，均证实了上述混凝土材料尺寸效应律的合理性。

而对于钢筋混凝土构件，由于多样的构件类型与形式(梁、柱及节点)，及复杂的钢筋-混凝土相互作用等，使得其破坏模式及破坏机理极为复杂[12-14,22-23]。因此，套用材料层面的尺寸效应律来描述钢筋混凝土构件破坏的尺寸效应行为是值得商榷的。另外，现有材料层面的尺寸效应律，亦仅仅粗略给出“结构尺寸”唯一因素的影响，不能反映钢筋混凝土构件破坏的其他重要因素对尺寸效应行为的影响。总体来说，对于钢筋混凝土构件层次的尺寸效应而言，应结合具体的破坏行为与破坏机制来建立钢筋混凝土构件的尺寸效应律。

本文在前期试验结果[24-25]的基础上，讨论了箍筋约束作用对混凝土柱破坏行为及尺寸效应的影响机制。结合经典的Bažant材料层次尺寸效应律，考虑箍筋约束作用对柱轴压强度及其尺寸效应的影响规律，提出了箍筋约束混凝土柱轴压破坏的尺寸效应理论公式。相关试验及模拟结果证实了该理论公式的合理性和准确性。

1 箍筋约束混凝土柱轴压试验

金浏等[24]和Du等[25]采用高径比为3的圆柱体试件，开展了不同截面尺寸箍筋约束混凝土圆柱的轴心受压破坏试验。采用相似比关系(1∶1.5∶2.25)设计几何相似的不同截面尺寸(Φ256 mm×768 mm、Φ384 mm×1152 mm、Φ576 mm×1728 mm)及不同体积配箍率(YA系列，ρsv=1.26%；YB系列，ρsv=2.89%)钢筋混凝土柱，相同参数试件均制作2个，共计12个试件。表1给出了试件的设计参数。箍筋的配置形式相同，且箍筋直径及间距与截面尺寸保持相同比例；为防止柱子两端发生破坏，端部箍筋进行加密设置。每个试件仅配备3根纵筋，其主要作用是固定箍筋。

表1 试件设计参数Table 1 Parameters of specimens

试验测得的名义轴压强度σNu随构件尺寸D(柱子的横截面直径)的变化规律如图1所示。结果表明：1)不同配箍率下，试件的名义轴压强度均随着截面直径的增加而降低，表现出明显的尺寸效应特征；2)随着配箍率的增大，箍筋的约束作用变强，试件的名义轴压强度越大；3)随着配箍率的提高，尺寸效应幅值减小，即强度减弱变缓慢。具体的试验结果与分析见文献[24-25]。

图1 约束混凝土柱名义强度与截面直径关系Fig.1 Nominal compressive strength vs cross-section diameter

2 细观模拟及结果分析

基于试验研究，本节将建立3D细观数值模型，对箍筋约束混凝土柱的轴压力学性能开展数值研究。在证实模型有效性的基础上，开展更大尺寸试件的模拟工作，进而更全面地揭示箍筋的约束作用对混凝土柱破坏行为及尺寸效应的影响机制。

2.1 细观尺度数值分析模型

2.1.1 细观数值模型建立

在细观角度，混凝土材料被简化为一种三相复合材料，由骨料颗粒、砂浆基质以及界面过渡区(ITZ)[26]组成。依据各组分的几何特征，运用Monte-Carlo方法，借助Fortran编程将骨料颗粒(假定为球体，最小等效粒径为16 mm，最大等效粒径为30 mm，体积分数约为30%)随机投放到砂浆中。考虑到计算量的影响，界面过渡区厚度设置为2 mm[27]，建立了素混凝土柱3D细观模型，如图2(a)所示。数值模型的加载方式采用位移控制，如图2(b)所示。

根据Du等[28]的研究，采用塑性损伤本构模型来描述砂浆及过渡界面的力学性能。假定砂浆和过渡界面主要因拉伸开裂和压缩破碎而破坏，用各向同性损伤变量描述拉伸和压缩损伤引起的刚度退化行为，其应力σ-应变ε表达式为：

式中：D表示各向同性损伤变量；为初始无损伤的弹性矩阵；ɛpl表示塑性应变张量。拉伸和压缩损伤状态分别由两个独立的硬化参数(压缩等效塑性应变)和(拉伸等效塑性应变)来表征。

骨料颗粒的强度较高，加载过程中相对于砂浆及界面过渡区不容易发生断裂破坏。因此，本文将其看作弹性体，假定外荷载作用下不破坏。另外，各相材料之间采用共节点方式连接，各单元节点位移连续，相邻单元之间位移可协调。

钢筋材料力学性能较均匀，故采用理想弹塑性本构模型来描述其力学行为。另外，在单轴压缩作用下，柱子破坏时钢筋与混凝土之间会产生滑移。为考虑钢筋与周围混凝土的非线性相互作用，钢筋单元节点和混凝土部分之间设置非线性弹簧(如图2(c)所示)，并采用我国《混凝土结构设计规范》[16](GB50010―2010)推荐的多线性τ-s曲线来描述，详见前文工作[27]。需要说明的是，该方法表示的粘结行为是一种宏观均质特性，没有考虑细观组分与钢筋之间的粘结性能的差异性。

图2 钢筋混凝土柱3D细观数值模型Fig.2 3D meso-scale simulation model of RC column

混凝土3种细观组分及钢筋力学参数，如表2所示。其中，骨料、砂浆及钢筋的材料强度及弹性模量等(“*”标注)可以根据试验实测值来确定，而界面过渡区的力学性质(“※”标注)不易测定。这里，通过对边长为150 mm的标准立方体混凝土试块开展大量单轴压缩试验来确定界面力学参数[27]。当界面过渡区的力学参数采用表2中数值时，混凝土单轴抗压强度模拟值是41.93 MPa，与试验结果42.8 MPa基本吻合，说明了参数选取的合理性。另外，对截面直径为150 mm、高度为300 mm的素混凝土圆柱体试件进行了模拟试验，得到的单轴抗压强度为34.76 MPa。

表2 数值模型力学参数Table 2 Mechanical parameters of numerical model

2.1.2 细观数值模型的验证

基于本文数值方法，对上述试验进行数值模拟，得到了不同尺寸不同配箍率试件的轴压破坏过程。以配箍率ρsv=2.89%的试件为例，如图3所示(直径为256 mm，损伤因子ω=0表示完好无损，ω=1表示完全破坏)。由于轴向压缩作用，损伤裂缝首先发生在模型中部，随后，裂缝逐渐延展，模型中的损伤区域进一步扩大。在峰值时刻，试件高度中部呈典型的压缩剪切破坏。而试件的端部由于约束产生的环箍效应，未产生严重破坏。模型受压过程中，同时发生横向变形，箍筋发挥约束作用，箍筋应变逐渐增大，部分箍筋达到其屈服强度，如图3(b)所示。模拟获得的约束混凝土柱破坏模式与图3(c)试验中试件的破坏模式[24-25]吻合良好。

图3 约束混凝土柱(直径为256 mm)损伤破坏Fig.3 Failure process of confined RC columns with cross-sectional diameter of 256 mm

图4分析了3根不同尺寸的配箍率为2.89%的箍筋约束混凝土模型的最终破坏云图。这3种试件的几何尺寸、箍筋直径及间距严格满足几何相似关系，且箍筋形式一致。可以发现：轴压作用下，相邻箍筋之间的核心混凝土压碎破坏，且破坏主要集中在试件中部区域。当尺寸小于384 mm时，模型主要呈现压缩破坏形态；而结构尺寸较大(直径576 mm)时，发生典型的压缩-剪切破坏形式，与试验结果[24-25]类似。另外，图5分析了试验及模拟得到的3种不同尺寸试件的应力-应变曲线，其中上升段与试验结果[24-25]吻合较好(名义应力为轴向荷载与横截面面积的比值，名义应变为加载端产生的竖向位移与试件高度的比值)，仅曲线下降段略有差别。曲线下降段的差别可能是采用的塑性损伤模型难以充分地反映约束效果所造成的。总体来说，数值模拟结果与试验结果吻合较为良好，说明了本文数值方法是可行的。

图4 不同尺寸箍筋约束混凝土柱破坏模式Fig.4 Failure patterns of stirrup-confined RC columns

图5 模拟与试验结果应力-应变关系对比Fig.5 Comparison of stress-strain relationships between numerical and experimental results

2.2 模拟结果及尺寸效应分析

2.2.1 模拟结果

在上述数值模拟结果与试验结果吻合良好的基础上，借助该数值分析方法对配箍率ρsv=0(即为素混凝土柱)的约束混凝土柱进行模拟，并模拟了更大尺寸(Φ864 mm×2592 mm)的约束混凝土柱。图6给出了数值模拟获得的不同配箍率、不同尺寸(相同参数的试件有2个，其骨料的体积分数相同，只有骨料的空间随机分布不同)的约束混凝土柱的轴压应力-应变曲线。

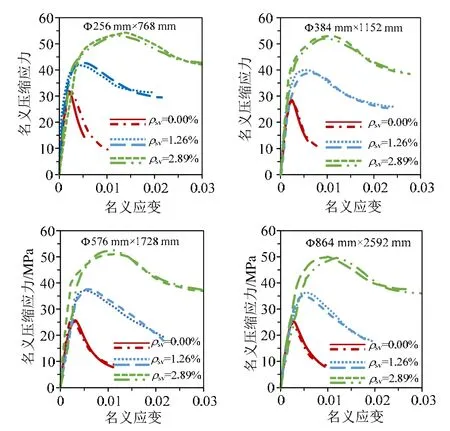
图6 约束混凝土柱轴压应力-应变曲线Fig.6 Stress-strain relationships of confined RC concrete columns

图6可以看出，相同尺寸的约束混凝土柱，峰值应力过后，素混凝土试件的应力-应变曲线下降快；而约束混凝土柱的应力-应变曲线下降缓慢，且体积配箍率越大，曲线下降越缓慢。这是由于箍筋的约束作用使混凝土内部裂缝的发展受到限制，提高了混凝土的强度和变形能力；体积配箍率越大，约束作用越强，混凝土的强度和变形能力提高的越多。

表3给出了约束混凝土柱名义轴压强度的数值结果与试验结果的对比。其中，S、M、L和U分别表示小、中、大和特大4种构件尺寸(特大尺寸为Φ864 mm × 2592 mm)，YO表示素混凝土柱。可以看出，模拟与试验结果误差小于 5%，两者吻合较好。其中，名义轴压强度σNu定义为：

式中，Pu、σNu、D分别是峰值荷载、名义轴压强度、截面直径。σNu为峰值荷载Pu时的名义应力值。

2.2.2 尺寸效应分析

图7给出的是在不同配箍率下，24根约束混凝土柱模型名义轴压强度与截面直径的关系。从图7可以看出，轴压作用下约束混凝土柱的名义轴压强度随着截面尺寸的增加而减小，即存在尺寸效应。素混凝土柱名义强度随尺寸降低明显，尺寸效应显著。对于约束混凝土，随着箍筋率的增大，柱的名义强度随尺寸降低速率减小，即约束混凝土柱模型的尺寸效应现象减弱。实际上这是由于箍筋约束作用的增强，使得柱破坏时脆性程度降低，削弱了尺寸效应。

表3 名义轴压强度模拟与试验结果对比Table 3 Comparison of nominal strengths between simulation and test results

图7 名义轴压强度与截面直径关系Fig.7 Nominal compressive strength vs cross-section diameter

如引言所述，对于混凝土材料层次尺寸效应问题的研究，已有多种尺寸效应理论[19-21]。其中，Bažant在断裂力学理论的基础上，提出了适用于混凝土材料的尺寸效应公式[19]：

式中：σNu为名义强度；fc为混凝土材料抗压强度(这里取最小尺寸素混凝土柱的抗压强度模拟值)；B、D0是依赖于结构的几何常数；D是试件尺寸(这里为柱直径)。式(3)转化成线性方程：

表4 Bažant尺寸效应理论拟合参数Table 4 Parameters of Bažant size effect law

图8分析了素混凝土模型的名义强度数据与ažant尺寸效应律(SEL)的拟合结果。图8中：水平线代表塑性强度理论(Strength criterion，不考虑尺寸效应)；斜线代表线弹性断裂力学理论(LEFM)。拟合相关系数Rxy=0.92，说明Bažant尺寸效应律能够较好的描述素混凝土柱轴压强度的尺寸效应规律。

图8 素混凝土柱数值结果回归分析Fig.8 Numerical data regression analysis of plain concrete columns

实际上，Bažant的尺寸律主要适用于所谓拟脆性断裂(pseduo-fracture)，其理论基础本质上来源于断裂力学(发生在断裂过程区的断裂)，在原理上来说是不适合于箍筋约束混凝土柱的。

3 尺寸效应理论公式

3.1 轴压强度尺寸效应理论公式

实际上，箍筋约束混凝土柱在轴压加载下的承载力N由两部分承担：1)纵筋的承载力Ns；2)无纵筋混凝土柱承载力Nsc(即，仅含箍筋的约束混凝土柱)。根据该两部分的贡献，柱的总承载力N为：

其中：

式中：为纵筋的抗压强度设计值；As为全部纵筋的横截面面积；Ac为钢筋混凝土柱横截面面积；σNu为无纵筋约束混凝土柱的名义强度。

由式(5)可知，仅第 2部分所贡献的承载力Nsc(或名义强度)与柱尺寸、箍筋率、柱截面形式及箍筋间距等因素相关，即与尺寸效应有关；而第 1部分(Ns)为纵筋承担部分，因此与结构尺寸无关。

根据第2节和第3节给出的试验及模拟结果，不难得出，箍筋的约束作用对约束混凝土柱轴压破坏行为的影响表现在以下两个方面。

1)名义轴压强度的增强作用。由于约束作用的存在，约束混凝土柱的名义轴压强度较素混凝土柱有显著的提高；且箍筋率越大，名义强度越高。此作用可用强度提高系数φ来表征。

2)尺寸效应的削弱与抑制作用。由于箍筋的约束作用，混凝土处于三轴受压应力状态，箍筋内部混凝土的变形被限制，柱的延性能力增强，脆性程度降低，约束混凝土柱尺寸效应削弱。当约束作用极强时，整个约束混凝土柱的轴压破坏表现为塑性破坏，此时尺寸效应完全消失[13,19]。该行为可用尺寸效应削弱系数β来描述。

由于钢筋混凝土构件层次的破坏机制与机理远比混凝土材料层次复杂，箍筋约束混凝土柱尺寸效应的影响因素很多。另外，Bažant材料尺寸效应律仅能体现“试件尺寸”唯一因素的影响，不能够定量的描述配箍率等参数对尺寸效应的影响。

基于以上基本认识，在Bažant材料层次尺寸效应理论的基础上，考虑箍筋的约束作用对尺寸效应的影响，建立构件层次箍筋约束混凝土柱轴压强度尺寸效应理论，提出如下的半经验-半理论公式：

式中，参数φ和β均应为箍筋率的函数。另外，式(7)反映了约束混凝土柱(构件层面)尺寸效应定量规律与混凝土材料层次尺寸效应规律之间的关联性。

3.2 尺寸效应公式相关参数的确定

3.2.1 强度提高系数φ的确定

20 世纪70年代至今，工程科研领域对箍筋约束混凝土的研究有了长足的发展。国内、外众多研究者，包括 Mander等[6]、Kent和 Park[6]、Sheikh和 Uzumeri[8]、过镇海等[10]、钱稼茹等[11]提出了各自的简化计算模型。

针对图9所示的箍筋约束状态下混凝土圆柱截面上的不均匀约束情况，Mander[6]等提出的模型得到广泛的认可。该模型提出了用有效约束系数ke来表征箍筋的有效约束力，即为相邻箍筋中间的横截面有效约束面积与混凝土核心区面积的比值。根据Mander等[6]的理论研究，可知圆形截面约束混凝土柱强度提高系数为：

式中：fcc为约束混凝土的轴心抗压强度；fc为素混凝土的抗压强度；fl为约束混凝土侧向压应力。根据Mander等[6]理论研究工作，可知圆形截面径向约束应力fl为：

图9 箍筋约束状态下混凝土有效约束区Fig.9 Effectively confined core for circular hoop reinforcement

式中：ρsv为横向钢筋体积配箍率；fyh为横向钢筋的屈服强度；ke为有效约束系数，可由下式获得：

式中：s＇为相邻箍筋净距；ρcc核心区纵筋配筋率；ds为箍筋中心线包围的截面直径。

本质上来说，强度提高系数φ与箍筋的屈服强度、体积配箍率(包括箍筋直径、箍筋面积等因素)及混凝土强度等级有关。

3.2.2 尺寸效应削弱系数β的确定

如3.1节所述，由于箍筋的约束作用，柱的延性能力增强，脆性程度降低，约束混凝土柱尺寸效应逐渐削弱。箍筋率ρ越大，强度尺寸效应的削弱作用越为显著。图10给出了削弱系数β与配箍率ρsv的关系曲线，下面将对其进行具体说明。

图10 尺寸效应削弱系数β的确定Fig.10 Determination of weakening coefficient β

当ρsv≤ρsv,min时(ρsv,min为配箍率下限值)，箍筋率很小，箍筋约束作用很弱，此时配箍的存在对柱轴压破坏尺寸效应无影响，此时β=1。

当ρsv→ρsv,max时(ρsv,max为配箍率上限值)，箍筋约束作用很强，柱的轴压破坏呈现“塑性”特征，此时轴压强度的尺寸效应将被完全抑制[13,19]。该状态下，名义轴压强度与结构尺寸无关，此时对应的名义轴压强度应为：

联立式(7)、式(8)和式(11)，可得尺寸效应被完全抑制时的削弱系数β为：

当配箍率介于ρsv,min与ρsv,max之间时，由于箍筋的约束作用，柱名义轴压强度的尺寸效应逐渐减弱。实际上，这种尺寸效应的减弱行为是一种渐进行为。针对此，本文采用渐进曲线来描述该行为。也即是，在该配箍率之间，假定削弱系数β为一条起始于数值“1”，渐近于的非线性变化曲线，如图10所示。

图10所示的双曲正切曲线即为典型的渐进曲线之一，用来描述箍筋约束作用对尺寸效应的削弱行为。基于该假定与上述分析，可得削弱系数β的表达式为：

式中，α为调节系数，反映削弱系数β随配箍率变化的快慢，可通过试验和模拟结果数据拟合来确定。从式(13)可知，所建立的削弱系数的上限和下限具有明确的物理意义和力学意义。

3.3 半经验-半理论公式的验证

本节旨在讨论所建立的尺寸效应半经验-半理论公式的准确性和合理性。

综合式(7)、式(8)及式(13)可知，建立的尺寸效应半经验-半理论公式存在 3个参数需要确定，即B、D0和调节系数α。为方便起见，将标准尺寸Φ150 mm×300 mm素混凝土柱模型作为基准试件，其轴心抗压强度fc=34.76 MPa(表3所示)。将3.2.2节素混凝土柱模拟结果回归分析得到的尺寸效应参数B、D0作为基准参数，B=1.017，D0=800。

根据我国《混凝土结构设计规范》[16](GB 50010―2010)，体积配箍率下限值ρsv,min建议取为0.25%。

关于尺寸效应调节系数α，无法通过计算求出其解析解，这里采用与试验或模拟结果进行反复对比来确定。结合上述给定参数，将本文理论公式与试验结果[24-25]进行对比分析，发现：当调节系数α的值在6.0~10.0时，理论预测值与试验结果吻合良好，见图11。这里，建议α取值为8.0。该系数值反映尺寸效应削弱的快慢，因此它与混凝土强度等级及箍筋约束作用的强弱(如截面形式差异，约束程度不同)等都有密切关系。

在此基础上，为验证本文所建立的尺寸效应半经验-半理论公式的准确性，在上述已确定参数的条件下，将理论预测结果与更多参数工况(包括更大结构尺寸、更多配箍率)下的数值模拟结果进行对比，如图12所示。可以看出，图12给出的理论预测曲面可很好的与模拟及试验数据点吻合，证实了所提出的箍筋约束混凝土柱轴压强度尺寸效应公式的准确性。

图11 理论值与本文试验值的比较Fig.11 Comparison of theoretical results and present experimental data

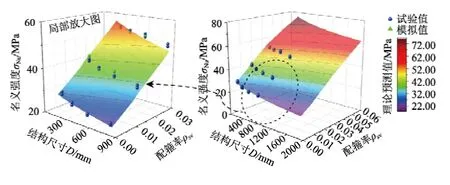
图12 α=8理论值与试验及模拟结果对比Fig.12 Comparisons between theoretical and numerical results

另外，为更充分的说明本文所建立的公式的准确性，本文搜集了更多的试验数据用作对比分析。图13给出了本文公式计算值与文献[29-31]中箍筋约束混凝土柱轴压破坏相关的试验数据的对比情况。从图13可以看出，本文尺寸效应公式能较好地预测圆形箍筋约束混凝土柱的名义轴压强度，再次说明了公式的准确性。当然，该理论公式的准确性尚需更多的试验及模拟结果来验证。

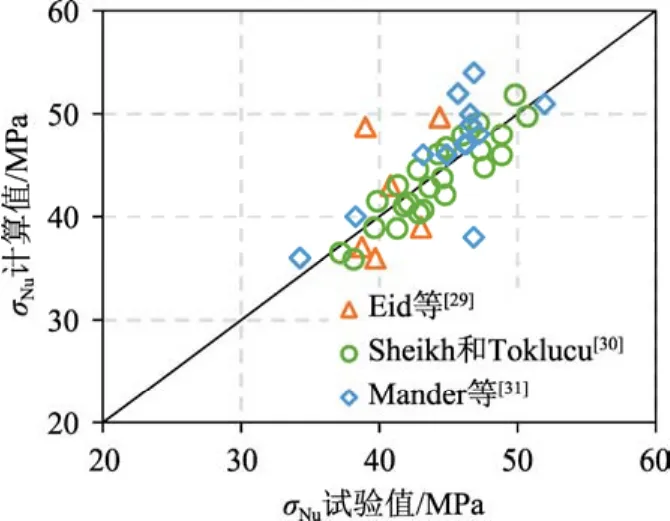
图13 理论值与其他试验结果[29-31]对比Fig.13 Comparison between theoretical and available test results in [29-31]

4 结论

混凝土材料层次尺寸效应理论已取得长足的发展，而在钢筋混凝土构件层次尺寸效应理论方面的研究则几近空白。

以箍筋约束混凝土圆柱为研究对象，在已有试验及相关数值模拟工作的基础上，首先凝练出了影响箍筋约束混凝土柱轴压破坏尺寸效应的主导因素——箍筋率，分析了箍筋率对柱名义强度及尺寸效应的影响机制与规律。结果表明箍筋约束作用对柱名义强度有两个方面影响，即增强强度和削弱其尺寸效应。进而在混凝土材料层次经典Bažant效应律的基础上，提出了可反映箍筋约束作用影响的钢筋混凝土柱轴压破坏尺寸效应半经验-半理论公式。相关试验及数值模拟结果亦证实了所提出的理论公式的准确性和合理性。值得一提的是，该理论公式可反映约束混凝土柱(构件层面)尺寸效应规律与混凝土材料层次尺寸效应规律之间的关联性。

需要说明的是，本文仅探讨了箍筋率对约束混凝土柱尺寸效应的影响，实际上配筋方式、混凝土强度等级、截面形式亦将影响柱的破坏行为；相关试验数据依然不够丰富，尚需要更多的试验数据(尤其是大尺寸柱试验数据)来验证所提出的半经验-半理论公式的准确性。