机会网络下基于价值评判的马尔科夫决策过程改进Epidemic算法*

曹 伟

（广东警官学院网络信息中心，广东 广州510000）

引言

机会网络 （Opportunistic Networks）［1］［2］主要应用于乡村网络、战地网络等不需要源节点和目标节点间存在完整链路的场景。在实际的机会网络当中，诸多原因可能导致网络不能连通。为应对这种情况，机会网络采取了“存储-携带-转发”的传输模式。现阶段的机会网络研究方向包括有路由算法［3］、缓存管理、移动模型等。Epidemic算法［4］是一种经典算法，本文以Epidemic算法为参照算法。该算法基于泛洪机制的方式，不加以区分消息节点，将数据复制到所相遇的每一个节点，最终将消息递交至目的节点。由于空间存储、带宽等资源是有限的，无限制的传递相同数据则会浪费有限的资源，从而降低机会网络的传输性能。同时在机会网络内可能存在恶意节点企图去攻击网络、延迟传输或毁灭数据。

基于上述原因，本文提出了一种在Epidemic算法的基础上，通过基于马尔科夫决策过程来构建机会路由的算法，为节点提供一种可靠的转发方法，对Epidemic算法进行泛洪控制，从而优化机会网络系统中的路由可用性和可靠性。

1 路由协议设计

1.1 算法总体设计框架

首先建立一个完全符合马尔科夫决策过程的机会网络模型。其中，建立的基于马尔科夫决策过程的节点转发策略：若当前相遇的节点为消息目的节点，则直接递交消息；否则在节点每次遇到一个节点后，对该节点进行综合价值计算和记录，当连续遇到前k个非目的节点后，将消息复制给之后遇到的第一个综合价值高于前k个已相遇节点的节点。此后清空价值记录表重复执行该流程，直到消息递交成功或消息生命周期结束。如图1所示。

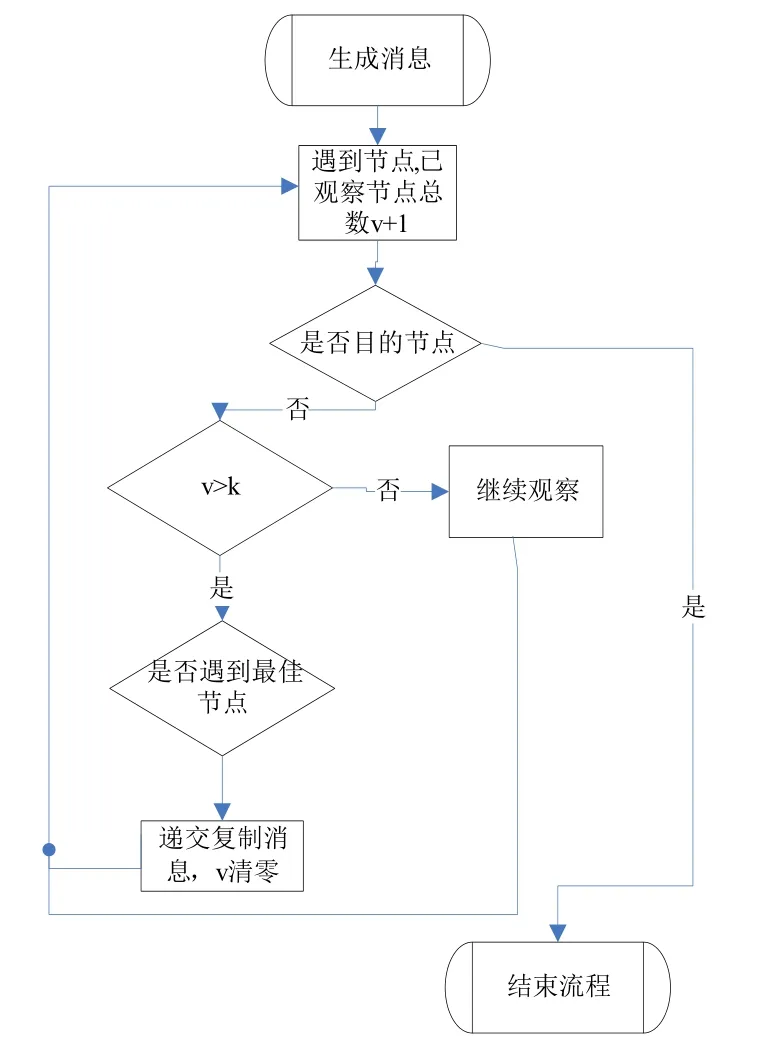
图1 算法总体框架设计

1.2 场景描述

如图2所示，在一片随机区域中，定义源节点s，目的节点e，场景中存在不同优先级梯度的节点n个。假定从节点s转发消息到节点e，则在综合价值梯度上s的价值最低，e最高。消息从节点s向节点e通过综合价值评判方式，从低向高的方向传输，通过相遇节点的综合价值，判断是否要进行消息转发。由于所有的节点都携带各种消息，以规则的移动模型进行运动与其他节点的相遇是随机的，因此符合离散时间有限阶段马尔科夫决策过程。

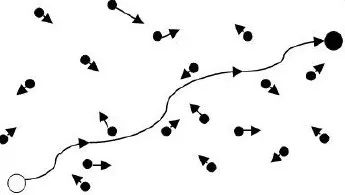
图2 机会网络传递过程场景

1.3 综合价值计算

本文综合价值通过节点之间的递交预测值进行分析。递交预测值的计算公式如下：

（1）概率的更新：对于节点a：

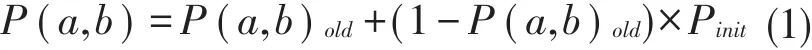
Pinit是递交预测值初始化常数，参考值为0.75；P(a,b)old为节点a,b在本次相遇之前的递交预测值。

（2）概率的衰减：对于节点a：

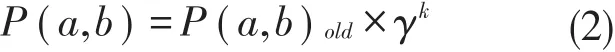
其中γ是衰减常数，γ∈(0,1]参考值为0.98；k是从上次衰减开始计算所经历的时间单元个数。

（3）概率的传递：对于节点a针对于其他任何一个节点c（c不包含相遇节点b）：

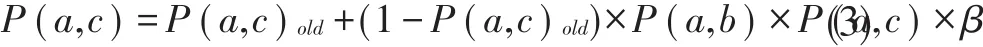
其中β是传递系数，参考值为0.25，递交预测值的传递，利用递交预测值的传递性更新。

1.4 受控洪泛设计

任一节点以马尔科夫方式移动，通过基于马尔科夫决策过程的消息转发策略构建模型。当消息源节点与其他节点相遇时，要对该相遇节点的综合价值进行判断，满足条件才转发消息至该节点上。定义马尔科夫决策过程状态集S，状态集S包含两个元素，分别为a和b，其中a表示当前与本节点相遇的节点不是目的节点，b代表当前与本节点相遇的节点是目的节点，因此S∈(a,b)。

定义状态转换集A(S)∈(x,y)，其中行动x表示跳过当前节点，并准备相遇下一个节点；行动y表示传送消息给当前节点。由马尔科夫性质可知，递交不依赖当前状态Snow，且只要采取行动x，该阶段的过程就不断持续。定义转移概率，在时刻t+1，恰好在前n+1个节点中遇到目的节点的概率是：

根据式(5)，则未遇到目的节点的概率是：

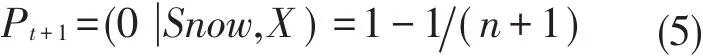
设节点总数目为n，消息转发策略为先观察k个候选节点，通过比较综合价值，记录最优节点Node(A)。在放弃前k个节点后，选择第1个优于Node(A)的节点Node(B)。k的求解过程如下：

对于某个固定的k，在总节点数目n确定下，如果最适合的节点出现在第i个位置k＜i≤n，且自k+1至i-1，各位置的节点综合价值小于前k位置中的最优节点，就要满足在前k个节点里含有在前i-1个节点中的最佳节点，共有k(i-1)个可能。考虑所有可能的i，在前k个节点之后能选中最佳节点的总概率P(k)：

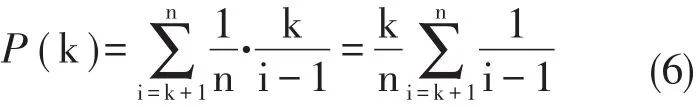
用x来表示k/n的值，并且假设n充分大，则上述公式可以写成：

对-x·lnx求导，并令这个导数为0，可以解出x的最优值，x=1/e。

因x=k/n且k是自然数，对结果取整：本文中的路由算法转发策略其核心思想是记录与消息节点相遇的前k个节点，若所遇节点为消息目的节点则递交消息；若在前k个节点中为消息目的节点，则记录最佳节点并放弃前k个节点，对剩下的节点范围内首次出现的优于被记录节点的节点进行消息传递。传递完成后，再次循环上述步骤直到消息传递完毕或生命周期结束为止。

2 性能评估

本实验通过在机会网络仿真平台ONE上实现，模拟区域范围为4500m×3400m；每个节点以蓝牙4.0协议传输，设定节点的传输半径10m；节点共分两组，由行人组1和行人组2组成，移动模型采用ShortestPathMapBasedMovement算法；缓存空间为50Mb；消息大小为512Kb-1Mb。行人移动速度为[0.5,1.5]km/h；消息产生间隔为25s至35s。并对仿真结果进行了比较。其他参数因仿真场景而不同,这类参数在具体场景设定。

2.1 投递成功率对比

通过对Epidemic和NewEpidemic两个路由算法进行仿真对比，设置节点总数分别为：100～200，每次递增10个，则同时对比相遇节点按计算37%、20%和50%的比较，结果分别如图3、图4、图5所示。

图3 不同节点数量下的报文成功递交率对比

如图3所示，NewEpidemic算法在选取37%的观察节点样本时的性能最优，而缺乏副本数量控制机制的传染路由（Epidemic）整体性能最差。在NewEpidemic算法中，随着节点数量的增加，报文成功递交率有波动但趋于稳定。与NewEpidemic-20和NewEpidemic-50算法相比，在NewEpidemic-37中，充分利用了节点的历史信息，使递交预测值的计算更合理、有效，从而使报文能更快更多地递交给目的节点，即提高报文成功递交率。

2.2 拥塞对比

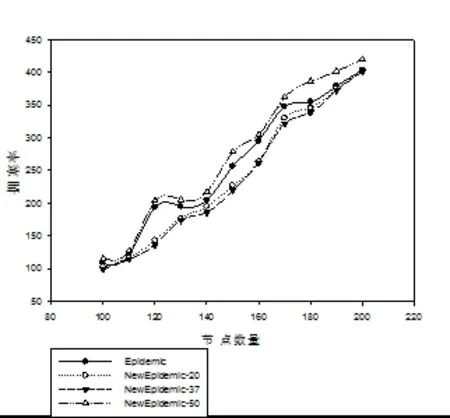
图4 不同节点数量下的拥塞对比

如图4所示的实验结果可以看出，在不同节点数量下容易发现NewEpidemic-37协议有一定的优势。随着产生节点总数的提升，尽管拥塞率上升，但NewEpidemic-37网络拥塞也保持较好的优势，能有效控制网络开销。

2.3 平均跳数对比

在计算平均跳数场景中，NewEpidemic-37协议具有较低的平均跳数，延迟较低。由实验结果可以看出，随着节点密度的提高，平均跳数增大，NewEpidemic-37协议保证了高效率的消息投递跳数。

综上，通过对比发现，NewEpidemic路由算法在观察37%的节点后，基于马尔科夫决策过程得出评判价值来构建机会路由的算法，为节点提供一种可靠的下一跳转发节点方法，对机会网络的性能具有保证，能够适应机会网络的复杂工作环境等特点。

3 结束语

本文在分析机会网络领域中现有的Epidemic路由算法特点和实际应用中存在的各种问题的基础上，针对Epidemic路由算法导致机会网络产生大量冗余数据的实际问题，提出了New-Epidemic算法。该算法基于价值评判的马尔科夫决策过程对洪泛进行控制。实验结果表明，NewEpidemic算法在不同节点数量分布的情况下均有良好的机会路由传输性能，提高机会路由的鲁棒性。