PROTEUS-MOC在TREAT试验堆稳态中子学计算中的应用

张广春 刘 杰YANG Won Sik

1（国防科技大学 并行与分布处理国家重点实验室 长沙 410073）

2（国防科技大学 复杂系统软件工程湖南省重点实验室 长沙 410073）

3

（University of Michigan，AnnArbor，Michigan 48105，United States）

TREAT［1］（Transient Reactor Test Facility）是由美国阿贡国家实验室（Argonne National Laboratory，ANL）设计的一种气冷石墨慢化反应堆，主要用于测试核材料和结构材料在瞬态工况下的性能。TREAT于20世纪50年代建造，1959年开始运行，1994年进入待命状态。福岛事故后，美国核工业界迫切需要研制先进的事故容错燃料（Accidenttolerant Fuel，ATF），以提高核电站在事故状态下的可靠性。为此，美国能源部在2017年对TREAT进行了重启，以对ATF燃料进行性能测试。在进行燃料性能实验时，TREAT会将部分燃料组件移出形成空腔，以使中子更容易达到堆外的中子辐射探测器上。因此，TREAT在中子学特性上表现为很强的泄漏性和非均匀性，对传统的三维中子输运计算方法提出了较大挑战。

当前的全堆输运计算以Monte Carlo方法［2］或确定论方法为主。Monte Carlo方法计算效率太低，一般作为基准验证方法使用。确定论方法的代表是二 维/一 维（2D/1D）特 征 线（Method of Characteristics，MOC）耦合方法［3-4］。这类方法在径向上采用MOC方法，轴向上采用低阶近似描述中子通量的行为，无法处理轴向强中子泄漏的问题。PROTEUS-MOC［5］是 由 ANL 在 NEAMS（Nuclear Energy Advanced Modeling and Simulation）计划支持下，为解决2D/1D方法的问题而开发的高保真三维中子输运程序。程序具有以下特性：1）在径向上采用二维MOC方法处理X-Y方向上的非均匀性，在轴向上采用一维间断有限元方法处理Z方向上的非均匀性，数学基础坚实，具有很好的计算稳定性，能够克服计算2D/1D方法在计算强中子泄漏问题时的不稳定性；2）径向采用非结构网格，具有非常好的几何适应性，可以对先进反应堆和实验装置中的复杂几何进行准确建模。为加速PROTEUS-MOC的计算，Jung等［6］提出了相容CMFD（Coarse-Mesh Finite Difference）加速算法，通过在CMFD方程中引入伪吸收截面，强制保证了每一个粗网中的中子守恒。Zhang等［7］在此基础上又进一步实现了相容pCMFD和Two-Level pCMFD（TLpCMFD）加速算法，以提高CMFD算法的稳定性和减少低阶方程的求解时间。

为测试PROTEUS-MOC程序对强中子泄漏问题的计算稳定性和计算效率，本文利用PROTEUSMOC对TREAT进行了稳态中子学计算，同时对TLpCMFD加速算法也进行了测试。

1 PROTEUS-MOC理论模型

1.1 PROTEUS-MOC的输运算法

稳态Boltzmann中子输运方程可写作如下形式：

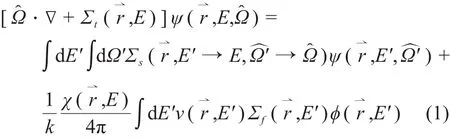
对式（1）应用多群近似及离散纵标离散，可以得到如下的方程：

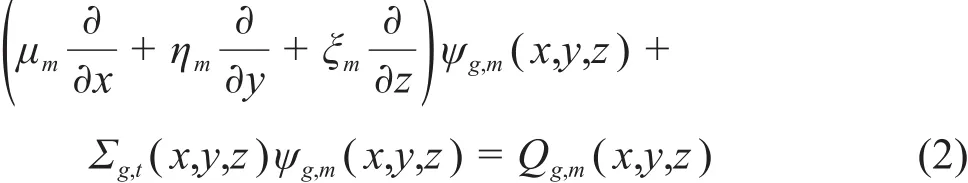
式中：m代表角度索引；g代表能群索引，在下面的推导中，为简洁起见，将省略能群索引g。将中子角通量和源在轴向的变化用一组线性正交基函数近似展开，如式（3）所示：

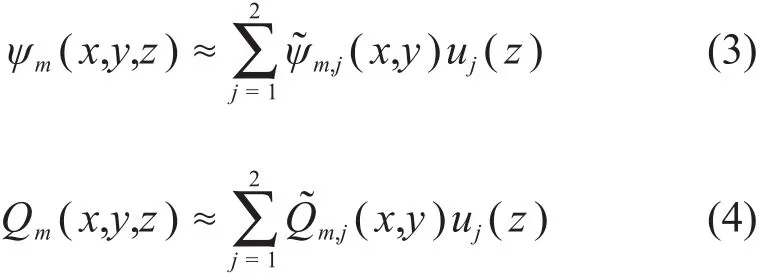
式中：uj(z)代表基函数；(x，y)和(x，y)分别代表角通量和源的展开系数。将式（3）和（4）代入式（2）可得：

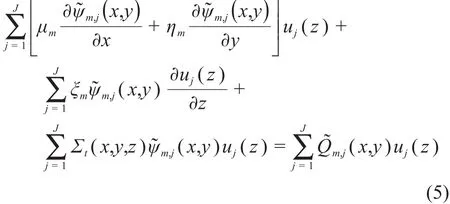
将带求解的问题在轴向上分层，并在第k层上第m个离散方向上应用间断伽辽金权重残差方法（假设该方向上ξm＞0），可以得到下面的一系列方程：

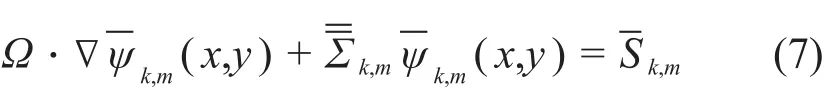
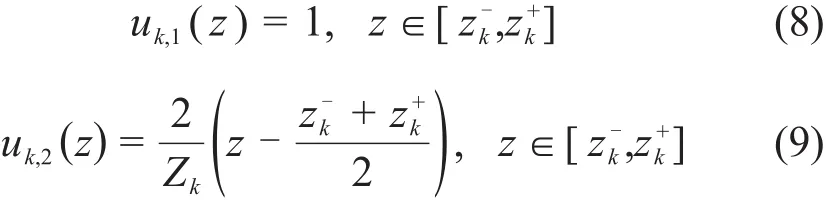
可以发现，式（7）与二维中子输运方程具有相同的结构，因此可以用二维特征线方法求解。求解过程也与特征线程序类似。将式（8）与式（9）代入式（6），可得的表达式如下：

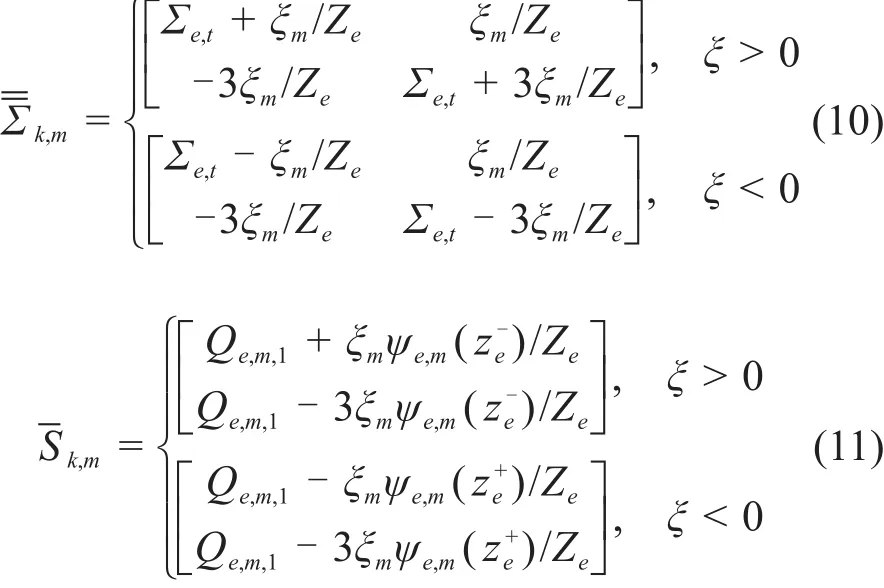
1.2 TLPCMFD加速算法

使用多重网格思想加速CMFD方程的求解在文献［8］中已由Smith等提出并测试。近年来，已有国内外多位研究人员将能量［9-10］或空间［11］多重网格方法用于加速CMFD或扩散方程的求解，取得了较好的效果。pCMFD方法由韩国Cho［12］等提出，利用了粗网边界上的偏流组装系数矩阵。随后，Yuk等［13］将pCMFD与空间多重网格方法结合提出了TLPCMFD方法，用于低阶方程的加速。TLPCMFD随后与文献［6］中提出的相容CMFD方法的思想相结合，并被实现在了PROTEUS-MOC程序中［7］。在TLPCMFD加速方法中存在着两层粗网：第一层粗网的尺寸一般小于一个栅元，在这层网格上求解的是一个固定源问题；第二层粗网的尺寸一般为一个组件大小，在这层网格上求解一个特征值问题。第一层的固定源问题和第二层的特征值问题之间可以迭代n次，用TLn表示。图1展示了PROTEUSMOC中的三层网络结构，图2展示了TLPCMFD中第一层加速和第二层加速间的迭代关系。TLPCMFD的详细推导见文献［7］。

图1 PROTEUS-MOC中的网格结构(a)用于MOC扫描的非结构网格，(b)1/4栅元组成第一层粗网，(c)燃料组件组成第二层粗网FigFig..1 1 Hierarchical mesh grids of PROTEUS-MOC(a)Unstructured mesh for MOC sweep,(b)The quarter-pins constitute the first-level coarse mesh,(c)The fuel assemblies constitute the second-level coarse mesh

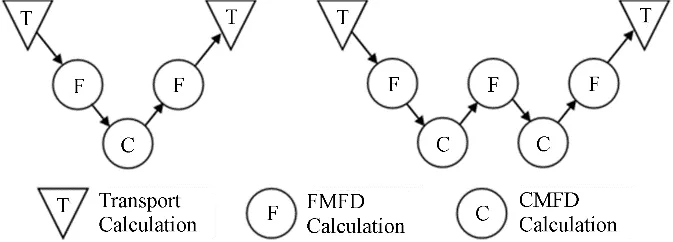
图2 TLPCMFD中第一层加速与第二层加速间的迭代关系Fig.2 Iterative relation between the first-level and secondlevel accelerations of the TLPCMFD method

2 计算模型

TREAT于1958年由ANL设计，位于爱达荷国家实验室（Idaho National Laboratory，INL），主要用于测试核反应堆材料在瞬态环境下的性能。该堆采用高浓铀（～93%）作为燃料，UO2颗粒弥散在石墨组成的慢化介质中，石墨和铀的原子比（C/U）约为10 000：1。TREAT中的燃料组件为方形，采用倒角设计，边长为10.16 cm，高度为121.92 cm，活性区上下均有石墨组成的反射层。燃料组件四周为锆合金组成的包围盒。根据实验目标和条件的不同，TREAT可有多种燃料布置方式，最多时可容纳361个燃料组件。本文选取了一种被称为M8CAL［14］（M8 Calibration）的堆芯布置方案为对象，利用PROTEUS-MOC对其进行中子学计算。在M8CAL的堆芯布置中，位于试验组件和堆外探测器之间的一排组件被全部取出，使得试验组件发出的中子更容易被探测到。该堆芯布置也因此具有很强的中子泄漏和非均匀性。M8CAL的堆芯布置如图3所示。本文计算所使用的网格和11群中子多群截面数据均来自文献［15］。

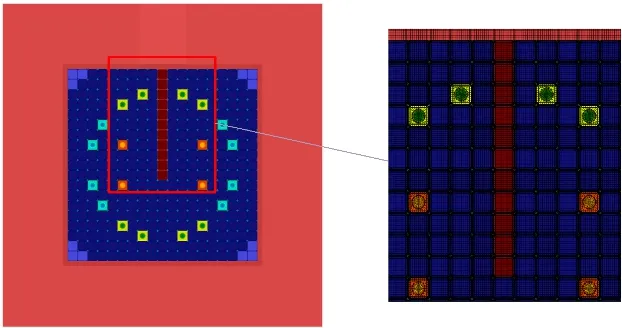
图3 M8CAL的堆芯布置及PROTEUS-MOC计算所使用的网格Fig.3 The core configuration of M8CAL and mesh grids used by PROTEUS-MOC

在实际计算时，裂变源的收敛准则设为1.0×10-6，特征值的收敛准则设为1.0×10-7。分别使用了pCMFD和TLPCMFD进行加速，以比较它们的效率差别。低阶方程的裂变源收敛准则设为1.0×10-9。在进行TLPCMFD加速时，每1/4个组件被设为一级粗网，全堆被划分为25个二级粗网。由于该模型较大，因此采用并行计算以提高计算效率，在角度、轴向层和径向网格三个层面上进行区域分解，共使用了480个核计算。详细的计算参数见表1，区域分解参数见表2，两层粗网设置见图4。

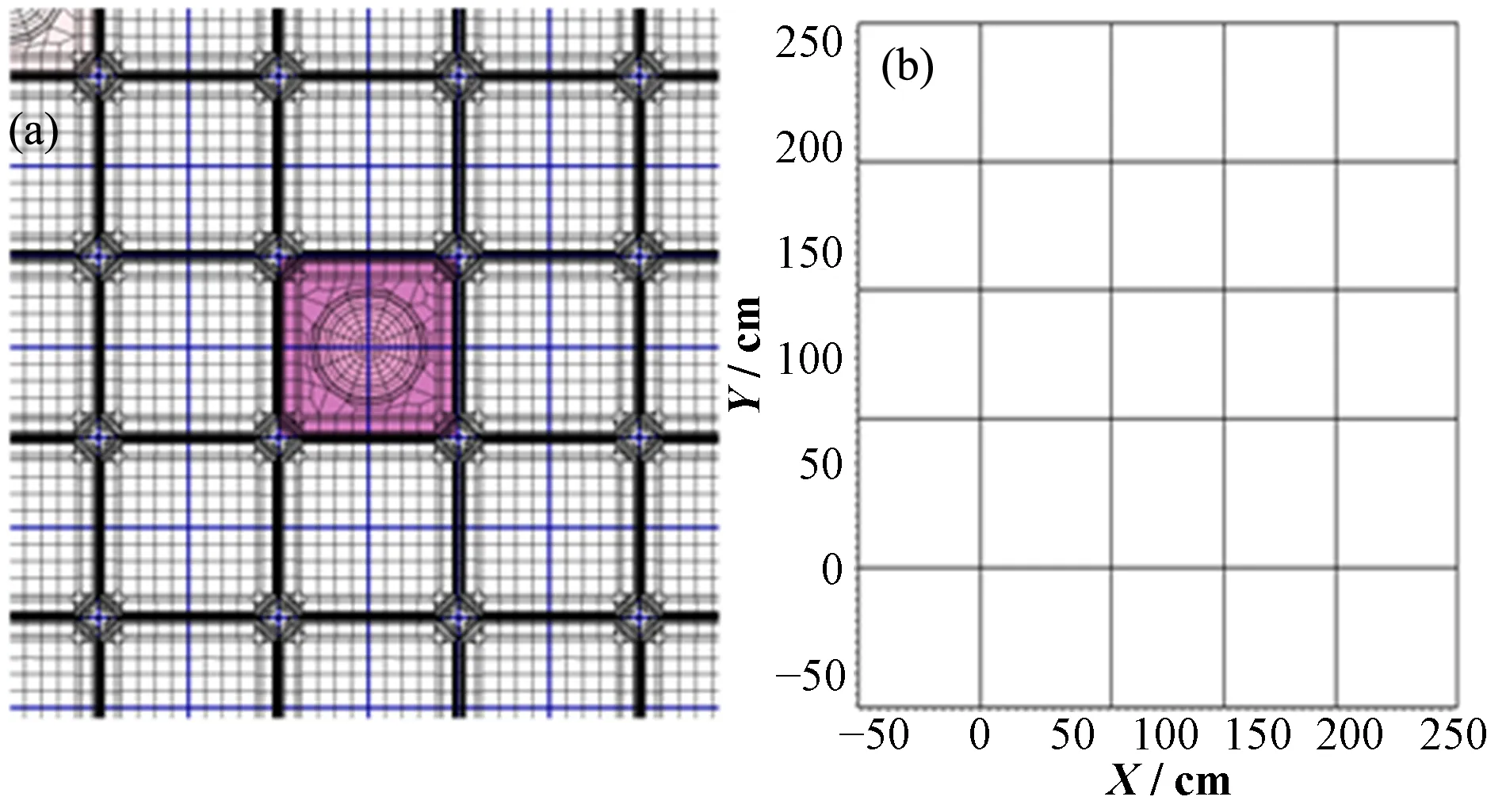
图4 用于计算M8CAL的两层粗网设置(a)第一层粗网设置，（b）第二层粗网设置Fig.4 The two level coarse mesh configurations for M8CAL calculations (a)First-level coarse mesh configuration,(b)Second-level mesh configuration

表1 M8CAL计算模型对参数设置Table 1 Discretization data of M8CALcore model

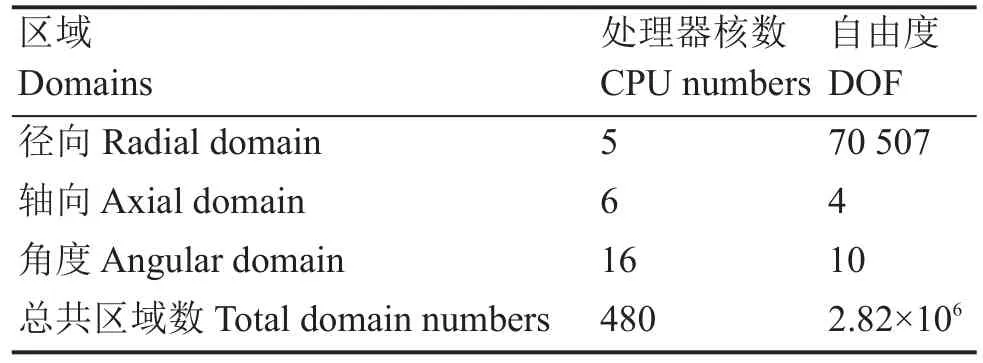
表2 区域分解的参数设置Table 2 Domain decomposition information

3 计算结果

利用PROTEUS-MOC程序，基于前述的模型参数，对TREAT反应堆的M8CAL布置进行了计算，并将计算结果与Serpent［16］的结果进行了对比。表3中列出了PROTEUS-MOC计算所得到的特征值，所需要的输运扫描次数和计算时间。

由表3可见，PROTEUS-MOC的计算结果与Serpent程序的结果符合得很好，相对偏差仅为0.12%。PROTEUS-MOC所使用的相容pCMFD加速算法表现良好，具有19.2倍的加速比。而TLPCMFD加速方法通过减少低阶方程的求解时间，可以进一步提高计算速度。采用TLPCMFDTL1加速的计算可以将加速比提高到25.2，但是输运扫描次数增加了55次，这说明TL1加速并没有充分挖掘出低阶加速的潜力。当使用TLPCMFD-TL2进行加速时，虽然低阶方程求解时间相比TL1略有增加，但有效减少了输运扫描次数，因此进一步将加速比提高到了26倍。图5给出了计算得到的M8CAL上的轴向积分功率分布。

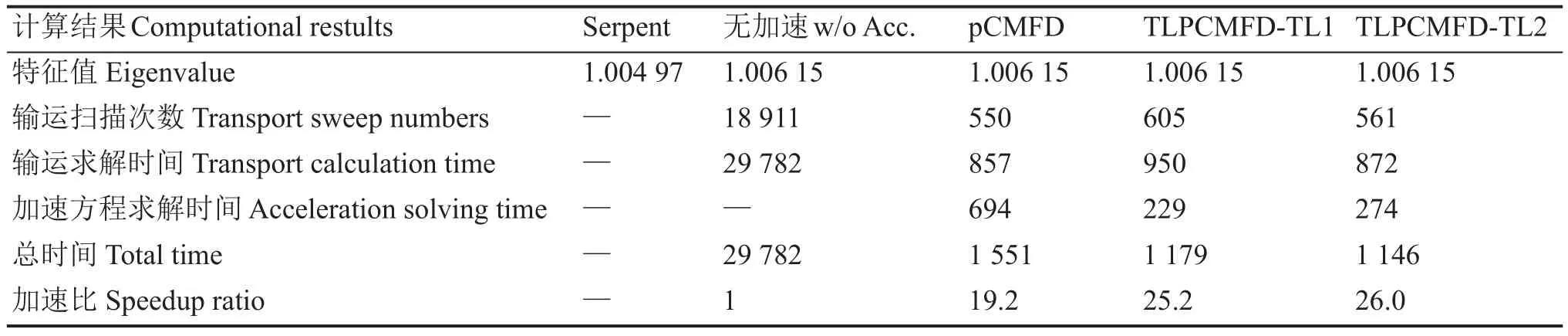
表3 M8CAL的计算结果Table 3 Calculation results for M8CAL

图5 M8CAL上的轴向积分功率分布Fig.5 Axially integrated fuel element power distributions of M8CAL

4 结语

为测试PROTEUS-MOC程序对强中子泄漏问题的计算精度和效率，本文以TREAT试验堆的M8CAL堆芯布置为对象进行了建模计算。计算结果表明：PROTEUS-MOC的计算精度较高，稳定性好，能较好地克服传统三维中子输运程序在强中子泄漏问题下的不稳定性。相比Monte Carlo程序Serpent的特征值结果，PROTEUS-MOC计算得到的相对偏差仅为0.12%。程序所采用的pCMFD和TLPCMFD加速算法表现优异，均可以较大幅度提高计算效率。相比pCMFD，TLPCMFD算法通过减少低阶方程的求解时间，将加速比提高到了26倍。以上的数值实验证明PROTEUS-MOC具有很高的工程应用价值，能够准确计算具有空腔结构和强中子泄漏的堆芯问题，可以很好地服务先进反应堆堆芯和堆内实验装置的设计与分析。