基于社会力模型的教学楼应急疏散数学模型的研究
2020-04-18郭小林
郭小林
(1、四川铁道职业学院,四川 成都611732 2、四川省应急管理学会,四川 成都610072)
随着我国教育事业的高速发展,学校是年轻人的成长成才的摇篮,也是祖国的未来和希望。教学楼是学生的聚集场所,具有楼层多、空间大、人数多的特点,在自然灾害、火灾、爆恐突发事件的情况下,要保护好学生的生命安全,需要把学生疏散到安全区域。
因此,快速有效的从教学楼内疏散学生,能极大程度的减少学生伤亡,推动我国教育工作健康长远发展。
1 教学楼疏散行为分析
应急疏散按照疏散人员的特征可以分为两类特征[1],个体特征和群集特征。个体特征就是考虑个体的行为差别,每个人都有自己的思考力、判断力以及体能差别,疏散模型就要按照每个个体的特征来设计,一个一个的疏散。群集特征就是将同一类相似的群体的疏散人员看成一个整体,他们有着相同的思维、体能和运动速度,一个整体一起疏散。
学校教学楼内的疏散人员有学生、教师和管理人员。经过对4.20 庐山地震时名山中学教室的疏散监控录像,总结了教学楼应急疏散的行为特征。应急疏散时,教师和管理人员具有高尚的师德和责任感,首先引导学生先行撤离,教职工自身才撤离。在学生的表现行为上,非常听从教师的指挥,有清晰的疏散方向和路线,虽然会发生拥挤但不会推嚷,疏散文明有序。在拥挤的时候疏散速度偏慢,不拥挤的时候疏散速度很快。在疏散过程中,教师的作用非常很大,持续指挥学生疏散,使得学生在心理上有很大的安全感,但学生心理还是表现出了一定的恐慌导致了拥挤,有少许学生不知所措,在得到老师指挥后能快速疏散。整个疏散过程在老师的有效指挥下井然有序。
2 数学模型的建立
在分析和研究了国内外大量的应急疏散模型后,结合教学楼疏散的特点,Helbing[2]提出了社会力模型比较符合教学楼疏散。
2.1 传统的社会力模型
社会力模型是基于恐慌疏散的动力学模型,模型当中考虑了每个个体的心理因素、物理因素、相互影响因素,利用牛顿运动方程建立了数学模型,如公示(1)。
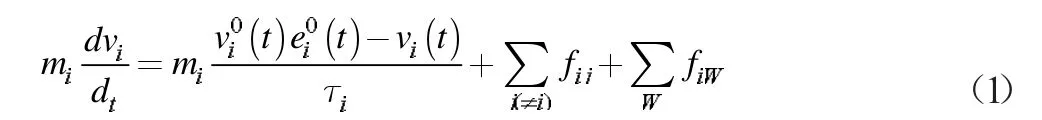
公式中mi表示人员i 的质量,vi(t)表示人员i 的失量速度,ei0(t)表示人员i 的期望方向,vi0(t)表示人员i 在期望方向的期望速度,τi表示改变速度的响应时间。
人员i 人员j 之间的相互作用力用fij表示,表达式为(2):

式中作用力分为三部分:Aiexp((rij-dij)/Bi)nij表示人员i,j的心理排斥力,Ai,Bi是常数;kg(rij-dij)nij表示身体排斥力;κg(rij-dij)Δvtjitij表示人员i,j 之间的摩擦力。dij=||ri-rj||表示人员i,j之间的模,nij=(n1ij,n2ij)=(ri-rj)/dij表示人员j 到人员i 的单位向量,tij=(-n2ij,n1ij)表示切向,Δvtji-(vj-vt)·tij表示切向速度差,k 和κ 为大常数,g 在人员i,j 不相互触碰的情况下取0,否则取一个参数x。
人员i 边界w 之间的相互作用力类似的分为三部分用fiw表示,表达式为(3):
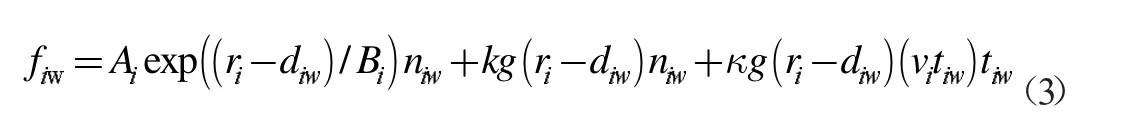
式中如果diw表示到边界w 的距离,niw表示垂直于墙的方向,tiw表示与墙相切的方向。
2.2 基于教学楼疏散行为优化模型
传统社会力模型中,把疏散人员各个方向的作用力都看作相等的,而人的所用了受视觉的影响非常大。通常情况下,人前方的物体产生的作用力比人后方的物体产生的作用大[3],但是后方的物体的影响力再小也不可能为零,也应有一定的影响。此时引入视觉作用因子ωi=(1-λi)+λi(1+cosθij)/2,其中λi(0>λi≤1)为影响程度,θij是人员i 的期望方向ei0(t)与人员i,j 的夹角。
传统社会力模型已经考虑到了疏散对象受到的各种作用力影响,但是从个体而言,就算两个个体处在同一个位置,由于心理素质的不同,面对突发事件会表现出不同的恐慌程度,两个个体的疏散行为有很大的差异。主要表现在疏散的速度上,越恐慌的人期望的速度越大[4]。根据教学楼实际疏散中,要求学生尽快撤离,离安全出口越远的学生焦虑最大,期望的速度最高。
因此,根据人员i 与安全出口的距离建立焦虑函数ρi=di0/dmax,修正期望速度为v0iρ(t)=v0i(t)+di0/dmax(νi-max-νi0(t)),式中di0为人员i 到安全出口的距离,dmax为疏散人员中离安全出口最远的人员距离,νi-max为人员i 的最大速度。
教学楼疏散的集群特征,分为两类疏散人群,理性冷静教职工和被疏散的学生。学生因为非常熟悉教学楼安全出口位置,在加上有老师的正确引导,期望方向和正确疏散方向能够达到一直,引起期望方向e0i(t)修正为ei,ei表示人员i 的正确疏散方向。
由于学生们长期生活在一起,师生和教室环境都非常熟悉,在疏散的时候不会因身体之间的接触以及和边界之间的接触而产生很大的相互作用力,因此取常数g=0。
2.3 教学楼应急疏散数学模型
以社会力模型为基础经过实际情况分析优化后,教学楼应急疏散数学模型如下:公示(4)
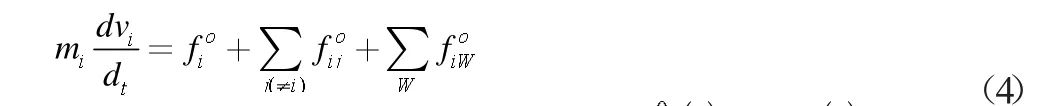

3 教学楼应急疏散的求解方法
3.1 模型的数学求解方法
教学楼应急疏散的数学模型理论上是微分方程求解,在根据运动规律求解出每个个体的疏散时间,最长个体疏散时间既是整个模型的疏散时间。求解结果为公式(5)

3.2 模型的计算机的求解方法
模型的数学理论求解在理论上是可行的,但是教学楼疏散的对象众多,而且模型还包含了人与人之间的心理相互作用力和人与边界之间的相互作用力,计算的复杂程度和难度非常大,几乎不可能用常规的数学手段求解。计算机可以编制计算程序进行大量计算和模拟仿真,因此上述数学要真正求解必须要借助计算机和专用程序实现,甚至需要用到专用计算机硬件支持。
经过调研,曾经计算过类似数学模型的计算机软件和方法包括PanicPackage 软件[5],纪庆革等提出的基于相对速度的社会力模型的人群仿真方法[6],基于MATLAB R2014B 用布谷鸟算法编程[7],基于MATLAB 软件采用mamdani 编程[8]等,可以按照软件方法编程求解。
数学模型和计算机编程求解是密不可分的,数学模型的优化有利于计算机的计算速度,计算机软件强大的计算能力使得数学模型求解成为可能,两者结合可以模型顺利求解。本文数学模型在具体的教学楼中应用时,需要要根据实际情况建立参数,如期望速度、期望方向、距离等参数,再利用计算机编程算出应急疏散所需要时间。再评估疏散的时间是否在安全的疏散时间内,如果疏散时间过长,则表明当前的教学楼运行状态不能保护学生安全疏散,则需要调整相应的参数,如减少学生人数,增加管理者的管理能力等等。
4 结论
本文的教学楼应急疏散数学模型可以应用于学校的应急疏散仿真、应急疏散能力评估、应急疏散方案的优化等等。模型还可以用于类似特征的建筑物如工厂车间、轨道交通空间的应急疏散。特别是大数据的应用发展,每个个体特征都可以准确的记录在后台数据中心,应用本模型可以实时仿真模拟应急疏散。本模型还可以融入到其他各种应用系统,为分析、预报、预警等提供可靠的数据。
