悬链锚泊线与海床接触作用分析

周恩蓬 林孝彩

（1、天津海运职业学院轮机工程系，天津300350 2、大连理工大学，辽宁 大连116024）

当上部平台往复运动时，锚泊线与海床土接触区域的锚链会随之提升或下降。该作用过程应力变化频繁，并且在分析时需充分考虑海床参数不定性及非线性因素，使得触地点成为锚泊线数值模拟和结构分析的难点。针对该问题的数值模拟方法，有频域方法，如采用等效水平弹簧[1]或线性耦合弹簧[2]模拟锚泊线和海床接触区域；有弹性基础方法，如Gatti-Bono C.等[3]将海床视为阻尼系数和刚度系数均为已知的弹性地基；另外还有提升着底法[4]等。国内外学者主要采用数值模拟的方法研究海床土作用，并依据自己的研究方法提出对应的本构模型。本文通过模拟锚泊线与海床接触作用得到动力响应，采用三种海床本构模型研究海床接触区域的应力，从而分析不同刚度海床模型对接触应力的影响。

1 数值模拟

1.1 参数设置

在本文中，锚泊线模型长度取为1200m，直径取为124mm；海床土体模型长为1200m，宽为30m，高为10m。锚泊线材料类型为线弹性，弹性模量为2.83e10Pa，密度为6841kg/m3，泊松比为0.3。采用三种海床本构模型：刚性海床、弹性海床、及应用双线性等向强化材料（BISO）模型的弹塑性海床。其中刚性海床弹性模量为2.5e15Pa，弹性海床为2.5e7Pa，BISO 模型假定等向强化和各向同性硬化，在应力- 应变关系曲线中，斜线段视为弹性部分，超出屈服点应力部分为塑性部分，如图1 所示。BISO 模型弹性模量为2.5e7Pa，即图中曲线的初始斜率，泊松比为0.4，屈服载荷为3725N。

1.2 有限元模型

应用ANSYS 进行有限元模拟时，锚泊线采用LINK180 单元，土体采用PLANE182 单元。接触对采用Targe169 和Conta175 单元，以点- 面接触方式来模拟接触关系，扩增Lagrange 法作为接触算法。在边界条件设置上，固定锚泊线左端，右端设为自由端；固定海床土的底面及四周，顶面设为自由端。

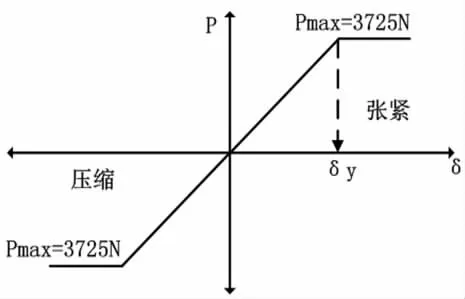
图1 土体本构模型（BISO）

在建模时，先将锚泊线整体平铺，如图2（a）所示，使其与海床土为全接触关系。然后在锚泊线右端点施加位移荷载模拟提升过程，计算得到顶端预张力，进而调整顶点在水平方向的位置，由此得到如图2（b）所示的锚泊线最终静平衡位置。在对有限元模型网格密度和求解时间步长进行精度分析后，最终确定触地点区域海床网格密度为1m，求解时间步长为5s。

图2 有限元模型

2 动力响应分析

动力响应求解过程涉及多种非线性因素，因此锚泊线相关研究多采用数值模拟的方法进行动力分析。除了能够模拟弹塑性变形、流体荷载、海床接触作用等非线性因素外，该法同时也能考虑流体加速度和锚泊线阻尼的附加时变效应。本文基于ANSYS 自带的非线性模块进行动力响应分析，对运动控制方程中的非线性项逐一考虑，采用时域方法得到锚泊线的应力时程曲线。

2.1 海况条件

对锚泊线进行动力响应分析时，可以将波浪长期作用视为若干个海况短期作用的叠加，各短期海况具有特定的特征参数，如波高、平均跨零周期等波浪谱参数及风速和流速。根据某海域波浪散布图[5]，选取典型海况进行计算，其波高为3.25m，平均跨零周期为5.5s，风速为11.93m/s，流速为0.344m/s。风向角和浪向角选为45°，流向角选为90°, 波浪谱选用JONSWAP 谱，谱峰因子取2.0。

2.2 应力时程曲线

在2.1 所述典型短期海况作用下，由AQWA 的水动力计算模块得到位移时程，并将其作为锚泊线顶端激励，根据锚泊线的竖向位移对接触点所在区域进行判断，根据各海况下接触点所处区域的分布特点，将编号为138、125、119、94、85 的5 个节点（即图3 中所示的A-E 点）作为研究对象进行接触分析。

依据上述方法，分别得到节点A-E 在各短期海况作用下的应力时程曲线。限于篇幅，只在图4 给出在典型海况下A 和E两个节点的应力时程曲线，其中海床本构模型分别采用刚性海床、弹性海床、弹塑性海床。

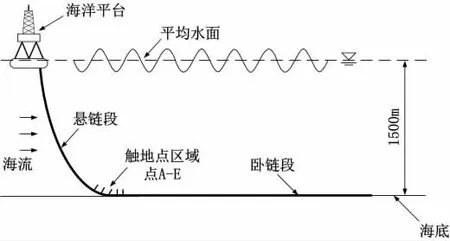
图3 触地点区域示意图

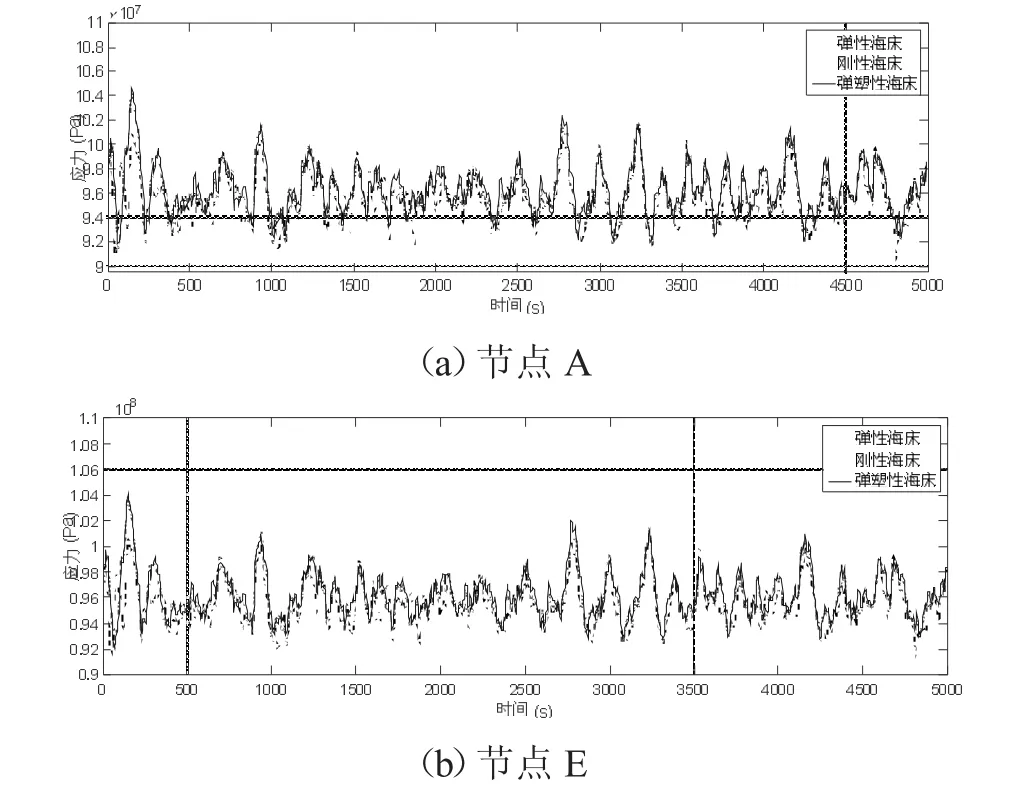
图4 典型海况下各节点应力时程曲线

3 结论

分别采用刚性海床、弹性海床、弹塑性海床三种本构模型对接触区域进行模拟，计算得到10 个短期海况下接触区域5 个特殊节点的应力时程曲线，分析海床刚度与接触应力的相关性，结果表明：在不同海床本构模型下，海床模型的刚度越大，锚泊线与海床接触区域的应力越大。今后可以选取其他不同的海床模型进行进一步分析，相关研究也可以拓展到张紧式锚泊系统。