多点思维，巧妙拓展——一道江苏函数模型题的多解与拓展

江苏省张家港中等专业学校 袁文娟

美国著名的数学教育家G·波利亚曾经说过：“观察可能导致发现，观察将提示某种规则、模式或定律。”在解决一些典型的高考数学真题时，我们要深入观察，多思维，巧变条件，妙拓展，往往会有意想不到的收获。下面围绕一道函数问题中的参数代数式的值的求解展开分析，以深刻体会一下深入观察的魅力。

分析：本题以分段函数的形式给出两个相应参数a，b所满足的不同函数关系式，结合指数函数与对数函数的关系式巧妙转化。如何建立起两参数a、b之间的关系，是破解问题的关键所在。通过对本题的深入观察与研究，发现可以从多个角度切入，采用多种方法来分析与求解。

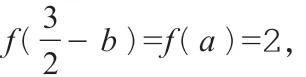
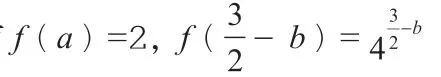
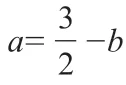
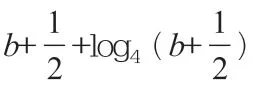
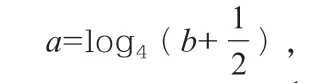
点评与拓展：其实，通过对以上典型数学问题的解决并深入观察，根据条件加以进一步拓展，可以进行深化与变式，从中发现问题、提出问题、分析问题并解决问题，真正达到“解一题拓一类，拓一类通一片”的效果，避免“题海战术”，从而真正培养学生思维品质，提升解题思维与解题能力，以不变应万变。

变式方向1：（变换常数）改变两个相应关系式中的常数为1，通过不同常数来进行变式

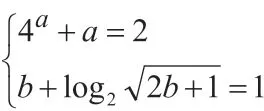
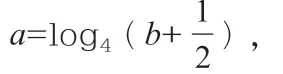
变式方向2：（变换函数）改变两个相应关系式中的函数关系，通过不同函数数来进行变式

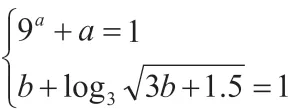
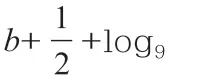
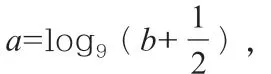
变式方向3：（变换一般性结论）改变两个相应关系式中的常数为一般参数，通过常数变参数来进行变式

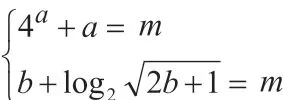
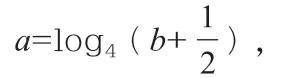
以上只是从两个特殊角度——改变函数的基本性质以及改变函数的关系式系数来进行拓展变形，其实，还可以从其他方面入手来进一步拓展与应用。美国著名数学家哈尔莫斯曾说过：问题是数学的心脏。对学生来说，如何确定解题思维，把问题归结到同一个熟悉的“问题”来处理是关键，也就是解题方法与技巧，以不变应万变，熟练解决问题。