基于渗水性改善的级配碎石空隙结构参数分析

2020-04-17赵方冉齐波石广顺刘军生

人民黄河 2020年1期

赵方冉齐波石广顺刘军生

摘要：为促进海绵城市建设，在广场等硬化地面设施建设中实现低成本开发，不仅充分利用雨水资源，而且有利于缓解城市排水系统的压力。这些设施建设工程中，碎石基層或垫层的渗水能力不但直接决定设施结构的稳定性，还影响其雨水渗蓄能力和自过滤能力;为使碎石垫层获得足够的渗水能力，需要使其内部空隙结构具有良好的分布状态，从而获得理想的渗水性与稳定性。通过分析不同排列的颗粒堆聚结构空隙参数，探讨了多级次组成对碎石堆聚结构空隙率和稳定性的影响规律;借鉴哈根一泊肃叶定律和达西定律，探讨了表达碎石堆聚结构空隙分布的叠筛模型，导出了上下层之间叠层空隙变化的计算公式。分析结果表明，级配碎石的渗水性与其结构中单孔渗流有效半径的二次方成正比，单位面积内上下叠层错位程度所决定的渗水有效系数与级配碎石的渗水能力成正比。

关键词：透水性：城市排水：级配碎石：颗粒级配关键比

中图分类号：TV314

文献标志码：A

doi：10. 3969/j .issn.1000- 1379.2020. 01.025

降雨期间的城市广场等地面硬化设施的雨水应尽快疏散，避免严重积水而影响地面设施的正常使用。同时为充分利用雨水资源和地表层结构的渗滤功能，从而获得低成本的水资源，需要对地表硬化层结构进行充分优化。随着我国海绵城市建设的不断发展，城市广场等各类渗水性地面硬化层结构的应用逐渐增多，而保障硬化层较好渗水性和结构稳定性的主要条件之一就是其基层或垫层结构的渗水性和结构稳定性。已有研究和实践表明[1-4]，大多数透水面层结构的失稳性破坏和透水性不良与基层或垫层结构性能密切相关，因此如何保证基层或垫层结构的渗水性和稳定性成为未来渗水性设施发展中必须解决的问题之一。

渗水性基层堆聚结构只有形成颗粒间较强的相互支撑性约束，才能避免其结构失稳。基层结构中的碎石颗粒大小和形状很不规则，当遭受来自面层的荷载作用时，部分颗粒在较高的应力集中作用下发生碎裂而造成局部失稳。工程实践表明[5-7].在颗粒堆聚结构中，较细小颗粒更容易产生接触应力作用破坏;基层结构的颗粒组成级配不良时，更容易导致结构产生失稳现象。同时，在积水环境中基层或垫层结构会因水的渗流而受到扰动，堆聚结构中相互粘结较弱的颗粒间连接较容易受扰动而失效，从而产生相对位移，导致结构失稳。因此，需要尽可能增强颗粒间的相互约束效应而抑制其相对位移造成的基层结构变形。

当颗粒堆聚结构中积水不能及时疏散时，外部荷载会对饱水基层结构内部施加频繁的动水压力，加剧基层结构的失稳。当垫层的渗水速度小于面层渗水速度时，由于难以及时疏散积水，因此可能造成外部荷载作用下的局部高动水压力，从而导致内部约束较弱颗粒产生松动或迁移，引起结构失稳。由此可见，良好的雨水疏散能力有利于基层结构的稳定性。基层或垫层良好的透水能力也是保证硬化层透水性的基本条件。此外可能因高压水流冲击面层结构而使其出现局部破损。

针对碎石结构稳定性和渗水性的影响，涂帅、李崸、袁峻[5-7]基于对级配碎石粗集料的形状、表面纹理构造等开展了相关试验研究，探讨了级配组成、含水量等因素对级配碎石动弹性模量和剪切性能的影响规律;Alemgena A.Araya研究了级配碎石基层的力学性能和渗水性能变化规律[8];J.Bear基于流体力学理论分析了碎石基层中多孔介质的渗流规律。这些研究成果阐述了影响级配碎石强度的诸多因素以及级配碎石渗水系数的评定方法，但尚未清晰表明级配碎石空隙结构与其颗粒级配间的相互关联性规律，尚需要基于碎石结构的细观空间参数优化来研究其结构稳定情况下的渗水规律，以便利用其影响规律指导碎石基层的级配选择，并通过改进碎石基层的级配结构来实现其渗水性能的最大化。

1 碎石级配对基层结构稳定性的影响

1.1 颗粒级配堆聚结构的空隙填充效应

碎石基层为不同组成的细观颗粒堆聚结构。级配填充理论认为，相同粒径的颗粒排列时，空隙率主要取决于颗粒的排列及填充方式，且间断填充结构的空隙率小于逐级填充结构。根据C.A.G. Weymouth的粒子干涉理论，为达到骨料间最大密实度，上一级颗粒之间的空隙要由次级颗粒所填充，剩余空隙再由更次级颗粒填充。依此类推，填充的次级颗粒粒径不得超过其空隙大小，否则上下级粒径骨料之间会发生干涉现象，从而降低堆聚结构的密实度。

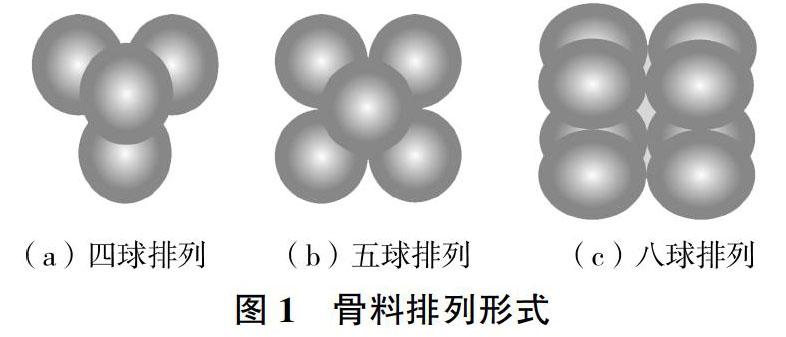
对于大量堆聚的碎石堆聚结构，若将碎石颗粒视为球状体，可近似表达级配碎石排列与填充方式对其结构空隙影响的基本规律。王峰、裴磊等[9-10]的研究结果表明，相同粒径的球体，其排列方式不同时，空隙率也不同;其空隙率与粒料粒径大小无关，而与粒料排列形式有关。堆聚球体的排列形式可分为四球排列、五球排列、八球排列等，见图1。这些排列形式均可形成相互约束的嵌挤状态，其中四球排列最为紧密，且颗粒之间的相互接触点也最多，而八球排列最为松散。

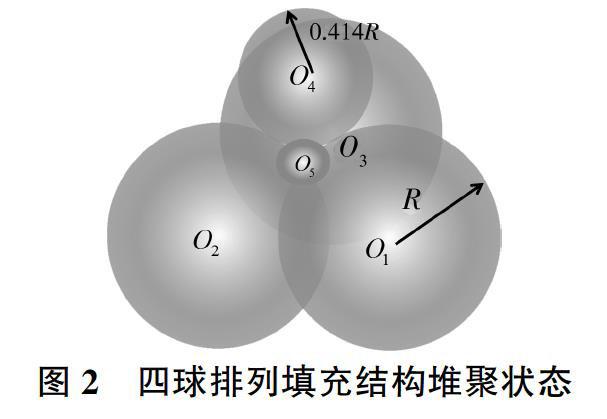
不同排列形式的结构状态分析表明，四球排列结构最为稳定。为进一步增强其结构稳定性，可在颗粒间空隙再填充次粒径颗粒。根据立体几何原理，直径为D的大球按四球排列时，填充其空隙的次球最大直径为0.414D;若需要再填充次球之间的空隙，则更小球的直径不得大于0.225D。以四球排列为例[11]，当相同球体按照四球错位排列时，则单粒级堆聚结构的空隙率为

可见，空隙率由单粒级的25.9%降为两粒级的20.7%.次级颗粒对堆聚结构空隙率降低显著。其堆聚结构的接触状态见图2。

其填充空隙率由47.6%下降为27.1%。可见，球体堆聚结构无论如何排列，以次级小球填充后，均可显著降低其空隙率[12]。

以上述四球排列为基础，若依次用较小球填充上级球之间的空隙，并形成五级粒径球体依次填充时，其空隙率见表1。由表1可见，随着颗粒级配级次的增多，颗粒间的接触点增多，其堆聚体越密实，结构的空隙率逐渐降低，则其渗水能力下降。显然，为保证级配碎石结构的渗水性，不能过度依靠增加颗粒级配级次来提高堆聚结构的稳定性。

1.2 颗粒级配对碎石基层结构稳定性的影响

碎石基层的稳定性需要满足两个条件：一是颗粒之间有足够的相互嵌挤约束而不易产生相对位移;二是碎石颗粒有足够的强度而不会产生剪切破碎。

为满足稳定性的第一项要求，应有适当的颗粒级配获得足够的接触点来约束颗粒的相对位移。对于单粒级球体堆聚结构，其周围三维分布的接触点为6个接触点，这种接触通常可以对其相对位移产生足够的约束，但考虑碎石颗粒的形状不规则可能造成部分颗粒因受到扰动而出现接触点少于6个的情况，需要有次级颗粒填充和嵌挤来增加颗粒间的接触点数，以提高其堆聚结构的稳定性。但从颗粒间的接触约束效果来看，过多级次的颗粒级配会产生接触约束冗余。因此只需要采用适当的颗粒填充级次获得足够的接触约束，就可以实现其稳定性。

为满足稳定性的第二项要求，除了选择强度较高的碎石外，还可以优化其颗粒尺寸和形状。已有研究结果表明[6-7].大粒径颗粒对基层骨架结构的形成具有关键作用，采用填充理论进行颗粒级配设计时，增大粒径可以显著提高颗粒间的传荷能力，从而间接提高交通荷载作用下的结构稳定性。因此选择较大颗粒碎石有利于结构稳定性。

由于碎石基層最大颗粒尺寸受到结构厚度和施工工艺的限制，因此最大粒级尺寸只能在其限制范围内选择。但是，级配碎石中较大尺寸颗粒占比具有较大的调整范围，需要通过调整碎石级配，降低级配关键比，增强级配碎石抗剪切破碎的能力，从而提高基层结构的稳定性。

2 级配碎石多孔结构的渗水性能分析

2.1 级配碎石堆聚结构渗水性能的影响因素

堆聚结构的渗水能力主要取决于其堆聚结构的空隙率和空隙分布特征。根据堆聚结构中空隙与外界的连通性，可划分为3类空隙，即对外全连通空隙、对外半连通空隙和封闭空隙。对外全连通空隙具有内部相互连通且与上下界面开放的结构特征，雨水渗流通过时的阻力很小，这类空隙主导着堆聚结构的渗水能力;对外半连通空隙内部相互连通，而与上界面或下界面之一处于开放状态，而与另一界面之间被封闭，该类空隙只能对渗入的雨水具有吸纳或缓冲能力，而不能将雨水直接渗出;封闭空隙因缺乏与外界开放的界面而使雨水不能出入，对基层结构渗水性的影响可以忽略。

相关研究结果表明[13-14]，当颗粒中最大颗粒粒径较大且粗颗粒比例较高时，其堆聚体可形成较为稳定的骨架结构，并可以形成较多的有效空隙，从而可获得较高的渗水性。而当细颗粒比例较高时，因细颗粒的堵塞效应而使堆聚结构的无效空隙增多，从而降低其渗水能力。为获得较高的渗水能力，透水性级配碎石基层应适当控制其细颗粒含量。

级配碎石结构的渗水性与空隙率密切相关，增大其空隙率可获得较高渗水能力。由表1可知，5级次颗粒级配碎石的空隙率比3级次颗粒级配碎石的降低21.5%.则其渗水性也会显著降低，可见，通过调整碎石的颗粒填充级次数，也可以影响其渗水性。

2.2 级配碎石堆聚结构的叠筛模型

图1中不同堆聚结构中的空隙错位排列方式有所差异，其中连通空隙在穿越堆聚层时会出现上下层间错位状态，从而使雨水下渗需要不断水平转向而形成弯曲的渗水路径。此外，由于次级颗粒的扰动效应使得雨水下渗路径在不同部位的水流正交面大小参差不齐，因此雨水沿碎石基层下渗时，水流路径弯曲不一，难以利用达西公式等反映规则路径的公式直接表达其空隙结构的渗水规律。

尽管碎石垫层的空隙结构不能利用规则通道的渗流参数来表达，但其水流方向仍遵守泄压原则，即水流方向正交面两侧具有由高压侧向低压侧流动的趋势。显然级配碎石结构中空隙形状不规则，正交面大小也在不断变化，使得其空隙体系中的雨水流速和方向都不稳定，但是某一瞬间在某一水平面所含空隙的雨水在级配碎石空隙中的位置可以确定，而这些雨水在下一瞬间所处的下一平面空隙位置也可以确定。依据不同瞬间的雨水移动位置变化，则可以将空隙渗流结构进行水平切割来反映不同瞬间雨水所处的位置，从而形成雨水流经不同截面空隙的众多断面分布状态，众多截面空隙叠加则可构成雨水的渗流路径。即基于某一瞬间水平切面上的空隙状态参数，可以描述其各部位的水流量和流动方向，从而可以将水流穿越级配碎石的渗透过程描述为大量瞬间状态的累加。由于每层切面均类似不同孔径分布的筛底，通过相邻筛底之间的空隙错位可反映水流在水平方向的流动，大量不同的筛底相互叠加就可以描述水流在空间上的渗流过程，因此可将该渗流路径表达方式定义为堆聚结构的叠筛模型（见图3）。

在叠筛模型中，碎石结构的空隙被看作水平面切割所形成若干平行的多孔筛叠加，从而形成空间不均匀分布的多孔渗水路径。其中，若干厚度为出的多孔平面，每一平面上分布有渗水等效半径为r的圆孔。不同平面间错开相叠所形成的孔径错位，可反映颗粒间因次级颗粒对渗流路径的扰动效应，相邻筛底叠合后可表达该堆聚结构的孔隙路径。

基于叠筛模型，水流路径分为两类：一类是在单独平切面上垂直下渗流到下一平切面上;另一类是在上下两平切面之间沿孔隙错位横向流动。假设在同一平面内的水流遵守哈根一泊肃叶方程的计算规则[15-16]，即单位时间内水通过其中一根毛细管的体积流量q为式中：μ为水的黏度;r为空隙渗流有效半径;dx为叠筛厚度;dp/dx为叠筛上下面间水压梯度。

水流由第一层筛流入第二层筛时，渗透量会有部分衰减，再进入下一层筛时又会有部分衰减，这种衰减可反映堆聚结构中孔隙形状和孔径变化所产生的阻滞效应。利用相邻各层平面直毛管错开相叠来反映这一衰减规律。

若以参数A表示水流通过叠筛模型进入下一层时的渗水有效系数。假设每个直毛管孔径均为r，每一层中毛管数量相同，则渗水有效系数可反映单一毛管的渗水有效系数，如每根毛管长度为L，则渗水有效系数就是管垂直截面积的反映。若将两层模型向下投影，其叠筛上下层相邻直毛管投影见图4。

令两圆相交部分的椭圆短轴长为a、长轴长为b.则上下平面错开距离为d=r-2a。其中单圆面积为Js.两圆相交的椭圆面积为S0，渗水有效系数反映为比例，且仅与面积有关。假设初始流入单孔水流量为q，由第一层流入下一层单孔孔径流量为qo，依次流入下一层单孔流量为q1、q2、…，其中减少的水流量为△q，则进入每一层单孔流量为

基于上述叠筛模型分析结果可知，堆聚结构中某一平截面上的空隙渗流系数主要取决于该截面上的空隙渗流有效半径r，并与该截面上的孔隙度p、两侧水头差△h以及上下截面之间的渗水有效系数△a+1有关，而λn+1又取决于上下层叠筛之间空隙错位程度。显然，对于由大颗粒组成的级配碎石，其上下叠层之间的错位则较大，使其渗水有效系数λn+1较小而不利于渗水。

此外，级配碎石结构中的有效渗水空隙率p_e主要取决于组成颗粒的形状及其相互嵌填密实程度，当颗粒之间错位嵌填且被挤压密实时，则其有效渗水空隙率p_e较小，从而不利于结构的渗水。

从上述规律来看，由于单孔孔隙渗流有效半径r的2次方与碎石层渗水性正相关，使得以大颗粒主导的碎石堆聚结构具有更高的渗水性。同时，对于细颗粒较多的堆聚结构，其渗水路径中上下叠层错位较小，此时结构的渗水有效系数λn+1较大而有利于结构的渗水，但其影响远小于单孔空隙渗流有效半徑r减小对渗水性的影响程度。

4 结论

（1）在级配碎石堆聚垫层结构中，碎石粒径越大，其结构稳定性越强;同时，随着颗粒填充级次的增多，颗粒间的接触点增多，堆聚体较密实，结构稳定性也较高。因此，适度增大碎石粒径尺寸，或颗粒填充级次.都可以提高碎石堆聚结构的稳定性。

（2）基于水流路径变化的叠筛模型分析，当级配碎石中粗、细颗粒较接近时，由于小颗粒的干扰效应而使其单孔空隙渗流有效半径r变小，且因大颗粒造成的层间渗水有效系数λn+1降低较快，从而降低了堆聚结构的渗水性能。

（3）基于颗粒堆聚结构叠筛模型的层间空隙变化计算分析，反映单位面积内上下孔叠层错位程度的渗水有效系数λn+1与渗水性成正比，间接表明较小颗粒占比较高的级配碎石在一定程度上也可以增大其结构渗水性。

（4）碎石堆聚结构中反映颗粒大小的单孔渗流有效半径r的2次方与渗水速度成正比，而多孔的综合渗水性只与上下孔叠层错位程度的渗水有效系数λn+1成正比。因此，采取以粗颗粒占主导的级配碎石堆聚结构对于增强堆聚结构的渗水性更为有效。

参考文献：

[1] 李敏，浅析水泥混凝土路面常见病害及防治措施[J].建材与装饰，2016（ 25）：230-231.

[2] 张宗阳，浅析水泥混凝土路面的破坏形式及防治措施[J].江西建材，2015（9）：145-146.

[3]史艳来，水泥混凝土路面断板的原因及防治措施[J].交通世界（建养·机械），2013（1）：124-125.

[4] 郑树庭，杨月萍，水泥混凝土路面裂缝产生原因及防治措施[Jl.内蒙古公路与运输，2012（5）：13-15.