基于偏微分方程和机器学习的图像去噪算法

杜渺勇，施 垚，周 浩，韩丹夫

(杭州师范大学理学院， 浙江 杭州 311121)

图像容易受到噪声破坏的特性，显示了去除噪声的必要性[1].近年来，小波分析和偏微分方程(PDE)在图像去噪领域得到了广泛的应用[2].现有的小波去噪方法主要有：非线性小波阈值去噪方法，基于树的小波去噪方法，多尺度小波去噪方法和小波系数模型的去噪方法[3].

现有的基于PDE方法的去噪模型主要有：P-M模型、全变分(TV)模型、四阶PDE模型等[4]，他们在进行图像去噪时能够很好的保护边缘信息，但是TV模型在处理高噪声的图像时会有过度平滑的现象发生，四阶PDE模型去噪时会轻易地使图像的光滑区域变的不再完整.

传统的PDE图像去噪算法需要一定的数学基础，为了降低设计PDE方程进行图像去噪的难度，Liu等人[5]提出了偏微分方程学习模型LPDE，将机器学习与PDE结合起来，但是这个模型收敛的速度非常慢，并且伴随着大量的计算和复杂的推导，为了解决Liu模型的缺点，Zhao等人[6]提出了一种新的方法，快速交替的时间分裂方法(fatsa)，新的方法减少了大量的训练时间和训练误差，并且去噪效果也比Liu的方法好. 本文在Zhao模型的基础上，通过减少微分不变量的个数，使训练的时间比Zhao的模型更快，并且去噪效果与Zhao的模型相差不多.

1 基于机器学习和PDE的模型介绍

根据Zhao[6]的模型，通过削减一个指示函数，减少与之相关的微分不变量，从16个微分不变量变为6个微分不变量，构建以下新的由微分不变量系数函数组成的PDE方程模型，对于二维图像，在二阶及以下有6个基本微分不变量，如表1所示.

表1 微分不变量的介绍Tab.1 Introduction of differential invariants

表1有6个基本微分不变量，它们的最高阶数是2阶. 这些微分不变量都有其几何意义，u是随着偏微分方程进行演变的图像，tr表示迹算子，u表示u的梯度算子，Hu表示关于函数u的海森矩阵，简记inv(u)=[inv0(u),inv1(u),…,inv5(u)]T，(·)T表示矩阵或者向量的转置.

基本微分不变量的线性组合是它们所能构成的最简单的函数[7]. 因此，学习偏微分方程可以转化为学习它们线性组合之后的系数[8]. 由基本微分不变量构成的函数，它们仅跟时间t有关，并且与空间变量是相互独立的.为此，可以准备一些训练用的输入与输出的图像对，通过最小化PDE和原始图像的误差来达到控制的目的. 我们设置初始函数作为输入图像，在Zhao的模型的基础上，提出以下新的由微分不变量系数函数构成的PDE方程模型，新的模型具体如下

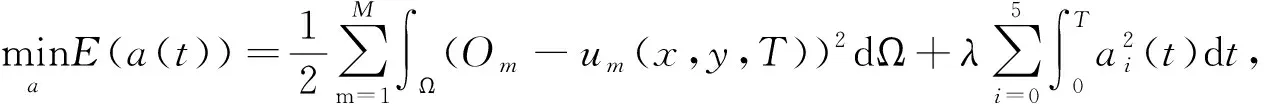
(1)

(2)

其中，{(Im,Om),m=1,…,M}为输入图像对，表示M个输入与输出的图像对的个数，um(x,y,t)是输入图像在t时刻的演变图像，Ω∈R2表示图像区域，T是可以归一化为1的时间跨度，Q=Ω×[0,T]，Γ=∂Ω×[0,T]，并且∂Ω表示Ω的边界，式(1)的正则项系数可以表示为a(t)=[a0(t),a1(t),...,a5(t)]T.其中，an(t)=an·t.

2 新的算法及步骤

为了解决新的模型，首先需要对时间变量t进行离散化，并且取步长为t，并且记ti=i·t，i=0,1,…N.在每一个tn，我们都最小化下面这个式子

(3)

(4)

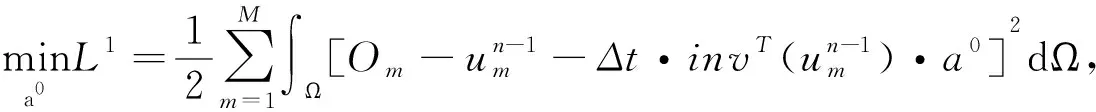
s.t.‖a0‖∞≤η1，

(6)

关于求解an-1，问题则可以转换为

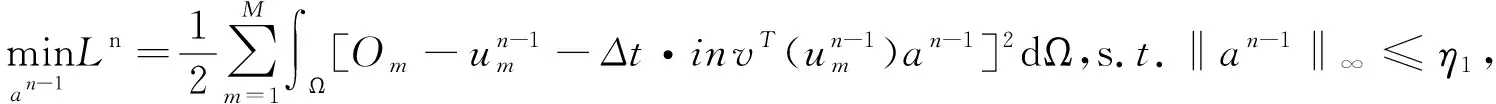
(7)

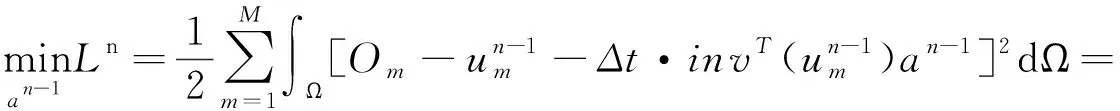
其中an与变量(x,y)相互独立，记

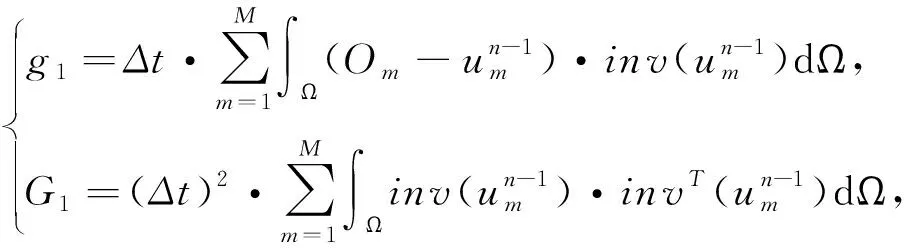
(8)

然后问题(7)就可以转化为以下问题：

(9)

问题(9)可以用信赖域方法去进行求解[10].

输出a0，a1，a2，a3，a4，a5.

3 实验结果与分析

3.1 实验设置

本文用中心差分来对导数进行估计：

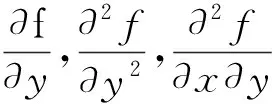
3.2 实验结果

图1 对图像添加标准差为30的去噪效果图Fig.1 Image denoising effect map with standard deviation of 30

表2 10张自然图像的平均峰值信噪比(PSNR)和程序所运行时间
Tab.2 Average peak signal-to-noise ratio of 10 natural images and running time of programs

Std新算法PSNR/(BI)fatsa算法PSNR/(BI)新算法运行时间/sfatsa算法的运行时间/s1032.63 dB33.42 dB52.17623.262030.33 dB30.82 dB58.36690.45 3027.88dB28.23dB67.42s783.68

3.3 实验结果分析

根据图1和表2，能够看出，随着高斯噪声标准差的增大，两种方法的去噪效果都有减弱.fatsa算法很好的保护了图像的细节信息，并且图像平滑自然，新的算法在部分图像细节中出现模糊. 新的方法虽然在去噪效果上要比fatsa算法有所减弱, 但是在运行时间上有了巨大的改进, 并且本文的PSNR与经过fatsa算法的PSNR相差不大.

4 结论

本文提出了一种新的机器学习与偏微分方程相结合的方法，它能够的有效的利用PDE来进行图像去噪，并且在fatsa算法基础上，通过减少微分不变量的个数，减少了迭代的次数.因为减少了正则项系数，所以图像去噪的结果与原模型相比还是有些许不足，并且这个模型并没有进行理论的证明，后期希望能够得到证明.本文只将这个模型用于了自然图像的去噪，后期还可能用于医学图像和卫星图像的去噪，以及其他图像的复原工作.