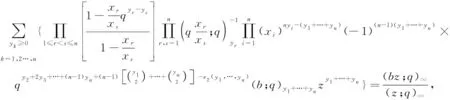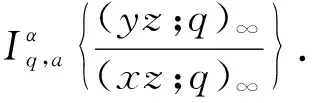关于分数阶q-多项式生成函数的注记
2020-04-17蔡利平
蔡利平,曹 健
(杭州师范大学理学院,浙江 杭州 311121)
0 引言
分数阶q-积分作为描述经典物理及其相关理论的数学分析工具,在数学,物理,工程科学[1-2]等诸多领域起着重要作用,通过分数阶q-积分的角度研究分数阶q-多项式的生成函数是探索特殊函数的一个有效途径.在这篇文章中,首先介绍一下q-级数的一些相关定义:
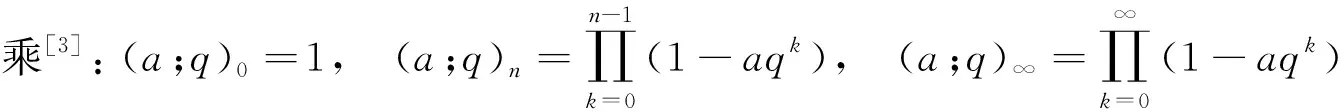
和(a1,a2,…,am;q)n=(a1;q)n(a2;q)n…(am;q)n,其中m是一个正整数,n是一个非负整数或∞.
q-二项式系数和q-二项式定理[3]:


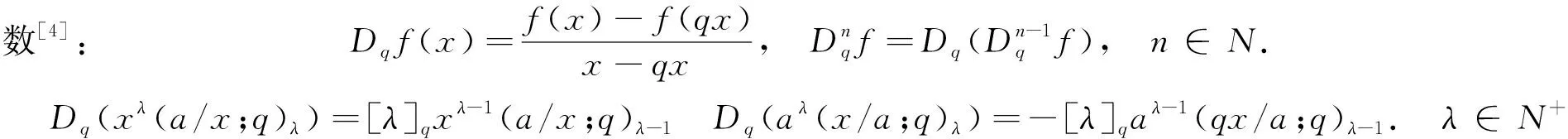
Riemann-Liouville分数阶q-积分算子[5]:
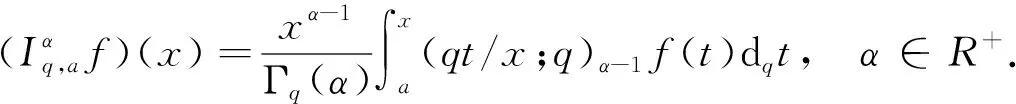
(2)
Predrag-Sladjana-Miomir[6]得到了以下的分数q-恒等式.
命题1[6]设α∈R+,λ,λ+α∈R{-1,-2,…},那么
其中Pλ(x,a)=xλ(a/x;q)λ=(x-a)(x-aq)(x-aq2)…(x-aqλ-1).
命题2[7]设α∈R+,0 (3) 定义1若α∈R+,k+α∈R{-1,-2…},我们有 (4) 注记在定义1中,令y=0,等式(4)变为等式(3). 接下来的文章,在第2部分中,我们用q-差分方程的方法给出了Predrag-Sladjana-Miomir拓广多项式和Al-Salam-Carlitz多项式的混合生成函数;在第3部分中,我们得出了Srivastava-Agarwal类型的Predrag-Sladjana-Miomir生成函数;在第4 部分中,我们得到了Predrag-Sladjana-Miomir多项式与罗杰斯多项式的混合生成函数;在第5 部分中,我们得到了U(n+1)型的Predrag-Sladjana-Miomir生成函数. Al-Salam-Carlitz多项式[8]在正交多项式中起着至关重要的作用,在函数、量子群和编码理论等众多领域中都有广泛的应用和推广.广义的Al-Salam-Carlitz多项式[10] Al-Salam-Carlitz多项式的生成函数[10-11] (5) (6) 在这一部分中,我们用q-差分方程的方法给出了Predrag-Sladjana-Miomir拓广多项式和Al-Salam-Carlitz多项式的混合生成函数. 定理1设α∈R+,0 (7) 定理2设α∈R+,0 (8) 推论1[7]设α∈R0,0 (9) (10) 注记在定理1与定理2中,令(y,s,t,u,v)=(0,0,0,s,t),等式(7)和等式(8)可变为等式(9)和等式(10). 引理1设α∈R+,0 (11) 证明引理1等式(11)的左边等价于 化简后等于等式(11)的右边,证毕. 引理2[11]设f(r,s,t,u,v) 是一个含有5个参数的函数,且(r,s,t,u,v)=(0,0,0,0,0)∈C3. u[f(r,s,t,u,v)-(1+q-1t)f(r,s,t,u,qv)+q-1vf(r,s,t,u,q2v)]= v{[f(r,s,t,u,v)-f(r,s,t,qu,v)]-(r+s)[f(r,s,t,u,qv)-f(r,s,t,qu,qv)]+ rs[f(r,s,t,u,q2v)-f(r,s,t,qu,q2v)]}. (12) (13) q-1u[f(r,s,t,u,v)-(1+q-1t)f(r,s,t,u,qv)+q-1vf(r,s,t,u,q2v)]= v{[f(r,s,t,u,v)-f(r,s,t,q-1u,v)]-(r+s)[f(r,s,t,u,qv)-f(r,s,t,q-1u,qv)]+ rs[f(r,s,t,u,q2v)-f(r,s,t,q-1u,q2v)]}. (14) 则可以得到 f(r,s,t,u,v)=∑∞n=0ηn·Ψ(r,s;t)n(u,v|q). 其中μn,ηn与变量r,s,t,u,v无关. 证明定理1令 (16) 由An和A0之间的关系,我们可根据等式(16)逆迭代得到 (17) 令等式(18)中u=0 ,由等式(11),我们得到 从而f(r,s,t,u,v) 等于等式(7)的左边,证毕.同样的,我们也可以推导出等式(8).定理2得证. 在这一部分中,我们利用分数阶q-积分得到了Srivastava-Agarwal类型的Predrag-Sladjana-Miomir生成函数. 引理3[12]设max{|t|,|xt|}<1,我们有 (19) 引理4[7]设α∈R+,0 (20) (21) 定理3设α∈R+,0 注记令λ=0,等式(22)可变为等式(11).令y=0,等式(22) 可推出等式(21).令λ=y=0,等式 (22)可变为等式 (20). 引理5[3]设max{|x|,|b|,|c|}<1,则有 (23) 证明定理3等式(22) 的左边等价于 上式通过等式(20)化简后,等于等式(22)的右式,证毕. Rogers-Szegö 多项式[13] (24) 在正交多项式的研究中有很重要的应用,它的推广生成函数 在这一部分我们得到了Predrag-Sladjana-Miomir拓广多项式与Rogers-Szegö多项式的混合生成函数. 定理4设α∈R+,0 (25) 定理5设α∈R+,0 (26) 推论2[7]设α∈R+,0 (27) 注记在定理4中,令(y,w,s,t)=(0,t,s/t,rs/t),等式(25) 可变为等式(27). 引理6设α∈R+,0 (28) 证明定理4等式(25) 的左式等价于 通过等式(28)化简后,等于等式(25)的右式.同样的,我们可以推导出等式(26).定理5得证. 许多学者已经建立了超几何级数与U(n+1)群之间的关系,详细内容可参阅[14-17]. Milne 研究了经典的贝利变换和贝利引理的U(n+1)型推广的理论和应用,其中还包含了非终止U(n+1)的二次项定理的推广. 命题3[17]若b,z和x1,…,xn都是不确定的值,并且n≥1.假设下列恒等式中没有一个分母消失,且0 (29) 其中e2(y1,…,yn) 是关于{y1,…,yn}的初等对称函数. 在这一部分中,我们得到了U(n+1)型的Predrag-Sladjana-Miomir生成函数的推广. 定理6若x,y和x1,…,xn都是不确定的值,并且n≥1.假设下列恒等式中没有一个分母消失,且0 (30) 其中e2(y1,…,yn) 是关于 {y1,…,yn}的初等对称函数. 注记在定理6中,令 (α,x,y)=(0,1,b) ,等式(30) 可变为等式(29). (31) 在等式(31)中,利用引理4和等式(11),经过化简后等价于等式(30)的右边,证毕.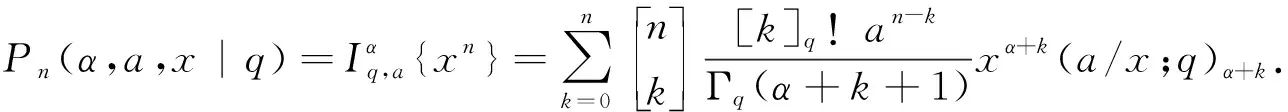

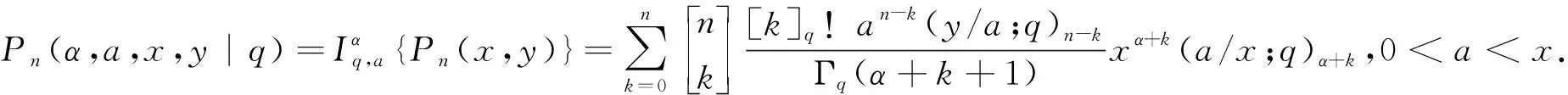
1 Predrag-Sladjana-Miomir和Al-Salam-Carlitz多项式的混合生成函数
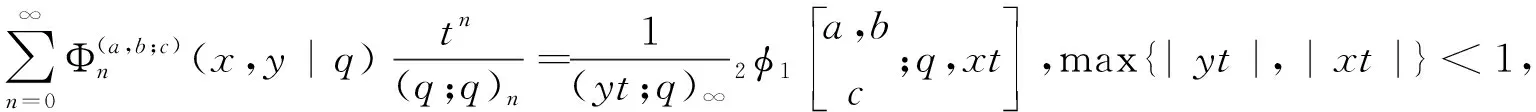
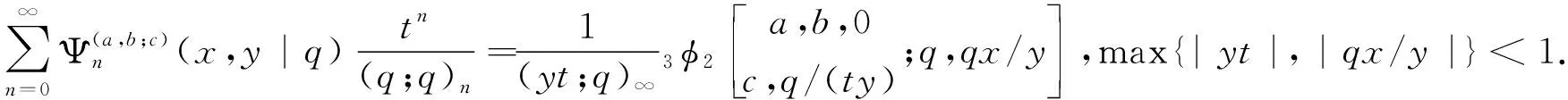

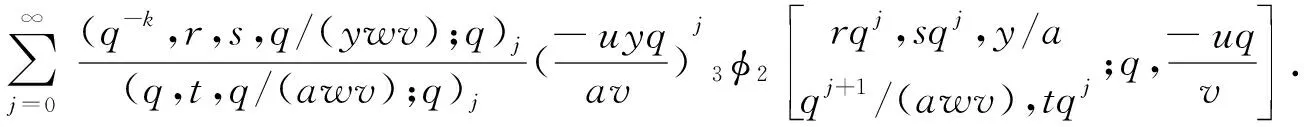
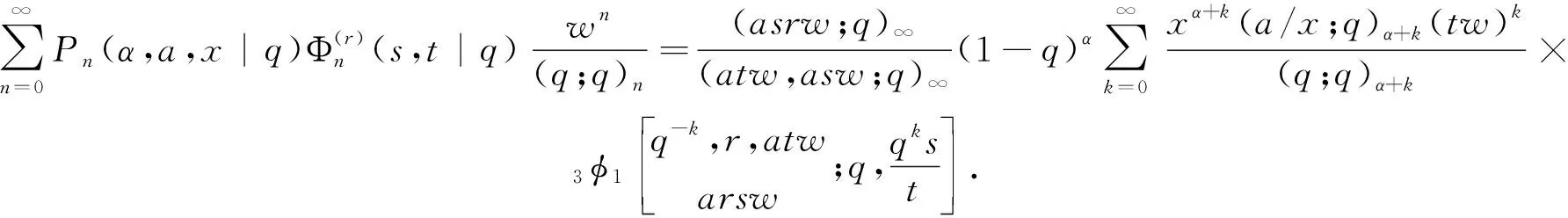

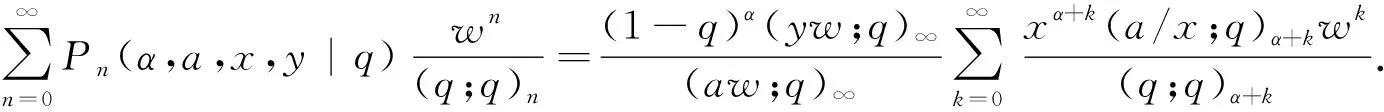
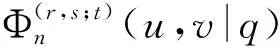
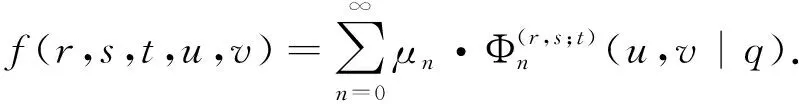
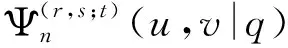



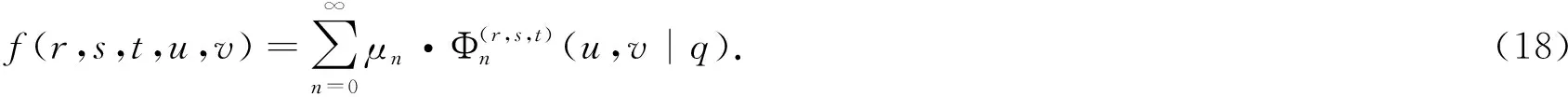
2 Srivastava-Agarwal类型的Predrag-Sladjana-Miomir生成函数

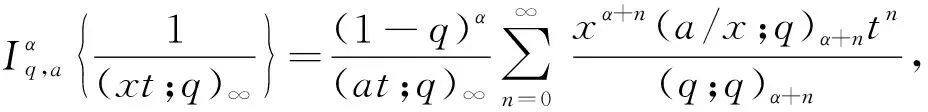
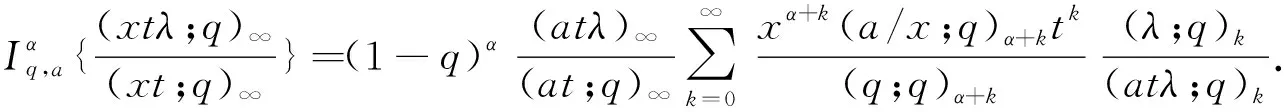

3 Predrag-Sladjana-Miomir多项式与Rogers-Szegö多项式的混合生成函数
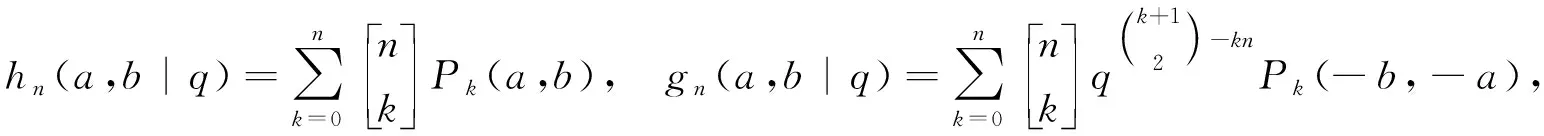
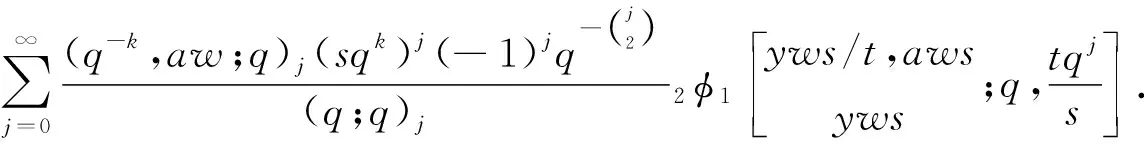

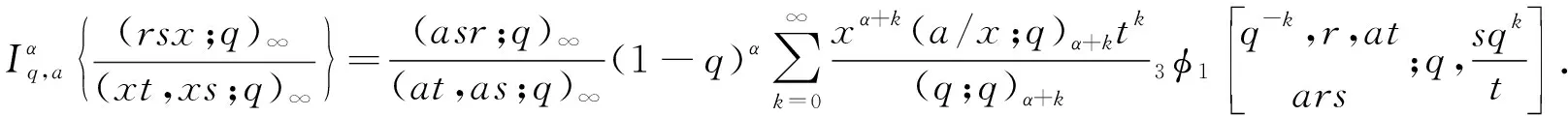

4 U(n+1)型的Predrag-Sladjana-Miomir生成函数