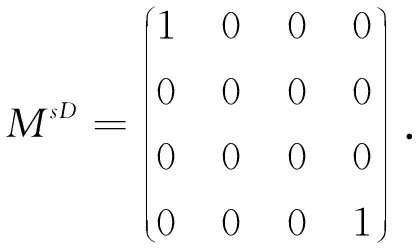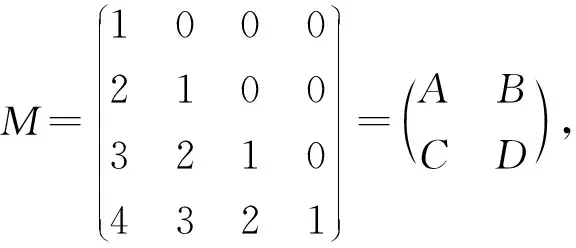两个复矩阵和的强-Drazin逆
2020-04-17张维玺陈焕艮
张维玺, 陈焕艮
(杭州师范大学理学院, 浙江 杭州 311121)
X2A=X,AX=XA,A-AX∈N(Cn×n).
这里X是唯一的,并且被称为矩阵A的强-Drazin逆.在本文中,若复矩阵A和B都具有强-Drazin逆,证明在条件A2B=0,BAB=0或AB2=0,ABA=0下,A+λB具有强-Drazin逆,并且给出了(A+λB)sD的表示形式.进一步应用该结论给出分块矩阵的一些对应结果.最后,给出例子来说明得到的结果.
0 引言
在本文中,Cn×n表示所有n×n复矩阵的集合,N(Cn×n)表示Cn×n中所有幂零元的集合.A∈Cn×n的Drazin逆是一个唯一的复矩阵X,表示为AD,并且满足AX=XA,X=XAX与A-A2X∈N(Cn×n).AΠ表示1-AAD,其中A∈Cn×n具有Drazin逆.一个复矩阵A∈Cn×n具有强-Drazin逆,如果存在一个复矩阵X∈Cn×n满足X2A=X,AX=XA,A-AX∈N(Cn×n).这里X是唯一的,并且称为A∈Cn×n的强-Drazin逆,在参考文献[1]中研究了强-Drazin逆.正如我们所知,A∈Cn×n具有强-Drazin逆当且仅当复矩阵A是两个可交换的幂零矩阵和幂等矩阵的和[2].
1 加性结果
本节的目的是确定复矩阵A+B何时具有强-Drazin逆,如果复矩阵A和B都具有强-Drazin逆.
引理1令A∈Cn×n,那么A具有强-Drazin逆当且仅当A-A2∈N(Cn×n).
证明由[2,引理2.1]和[1,引理2.2]易证.
引理2设A,B∈Cn×n都是幂零元,并且A2B=0,BAB=0.那么A+B是幂零元.
证明因为A和B是幂零元,所以存在正整数n和m,使得An=0,Bm=0.显然,(A+B)n+m+1的每一项可以写成形如Ar1Bs1Ar2Bs2…ArkBsk的形式,其中r1+r2+…+rk+s1+s2+…+sk=n+m+1且ri 情况1当r1=0时,上述形式可以写成Bs1Ar2Bs2…ArkBsk,我们有s1 情况2当r1>0时,我们有r1 综上可得,(A+B)n+m+1=0,所以A+B是幂零元.证毕. 定理1设A,B∈Cn×n都具有强-Drazin逆.若A2B=0,BAB=0,那么A+λB具有强-Drazin逆(λ为复数),并且 这里ind(A)=r,ind(B)=s. 证明由条件有A2(λB)=0,(λB)A(λB)=0,不失一般性,假定λ=1.我们需要证明A+B-(A+B)2是幂零元.考虑 A+B-(A+B)2=A+B-A2-AB-BA-B2=(A-A2)-AB+(B-B2)-BA. 因为A,B∈Cn×n都具有强-Drazin逆,由引理1可得,A-A2与B-B2都是幂零元. 令A1=A-A2,B1=-AB.那么 B1A1B1=(-AB)(A-A2)(-AB)=(-AB)(-A2B+A3B)=0. 令A2=(A-A2)-AB,B2=(B-B2)-BA.那么 B2A2B2=(B-B2-BA)(A-A2-AB)(B-B2-BA)= (B-B2-BA)(AB-AB2-ABA-AB2+AB3)=0 由强-Drazin逆的定义可知,若某元素的强-Drazin逆存在,那么它与该元素的Drazin逆是相同的.因此,由[3,定理2.2],我们可得 这里ind(A)=r,ind(B)=s.注意到(λB)SD=λ-1BSD.即得. 推论1设A,B∈Cn×n都具有强-Drazin逆.若AB=0,那么A+λB∈Cn×n具有强-Drazin逆(λ为复数),并且 这里t=max{ind(A),ind(B)}. 证明因为A,B都具有强-Drazin逆,并且AB=0,我们可得A2B=0,BAB=0.由定理1可得,A+λB具有强-Drazin逆. 这里t=max{ind(A),ind(B)}.证毕. 定理2设A,B∈Cn×n都具有强-Drazin逆.若AB2=0,ABA=0,那么A+λB具有强-Drazin逆(λ为复数),并且 这里ind(A)=r,ind(B)=s. 证明由条件知,A(λB)2=0,A(λB)A=0;不失一般性,假定λ=1.由引理1可知,我们只需证明A+B-(A+B)2是幂零元即可.我们考虑 A+B-(A+B)2=A+B-A2-AB-BA-B2= (-AB)+(A-A2)+(-BA)+(B-B2). 因为A,B∈Cn×n都具有强-Drazin逆,再次由引理1可得,A-A2与B-B2都是幂零元. A1B1A1=(-AB)(A-A2)(-AB)=0. 令A2=(A-A2)-AB,B2=(B-B2)-BA.那么 A2B2A2=(A-A2-AB)(B-B2-BA)(A-A2-AB)=(AB-A2B)(A-A2-AB)=0. 由强-Drazin逆的定义可知,若某元素的强-Drazin逆存在,那么它与该元素的Drazin逆是相同的.因此,由[3,定理2.1],以及(λB)SD=λ-1BSD即得. 本节的目的是给出分块矩阵具有强-Drazin逆的各种条件. 证明我们需要证明M-M2是幂零元.那么 因为A∈Ck×k具有强-Drazin逆,并且D∈Cl×l具有强-Drazin逆,我们可得A-A2与D-D2都是幂零元,所以存在正整数n和m,使得(A-A2)n=0,(D-D2)m=0.因此(M-M2)n+m+1=0.所以M-M2是幂零元,那么M∈Cn×n具有强-Drazin逆. 证明显而易见, 由BCA=0,BCB=0. 因此,由定理1可得,P+Q具有强-Drazin逆,并且 这里ind(P)=r,ind(Q)=s. 证明如果BC=0,DC=O,那么我们有BCA=0,BCB=0,DCA=0,DCB=0.那么,由定理3可得,M∈Cn×n具有强-Drazin逆,并且 证明如果CA=0,CB=0,那么我们有BCA=0,BCB=0,DCA=0,DCB=0.那么,由定理3可得,M∈Cn×n具有强-Drazin逆,并且 因为CBC=0,CBD=0,所以 因此,由定理1可得,P+Q具有强-Drazin逆,并且 这里ind(P)=r,ind(Q)=s. 证明若BC=0,BD=0,那么我们有CBC=0,CBD=0,ABC=0,ABD=0.那么,由定理4可得,M∈Cn×n具有强-Drazin逆,并且 证明如果AB=0,CB=0,那么我们可得CBC=0,CBD=0,ABC=0,ABD=0.那么,由定理4可得,M∈Cn×n具有强-Drazin逆,并且 本节的目的是说明我们前面已经证明的结果.
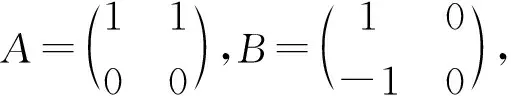
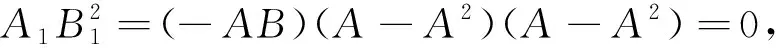
2 分块矩阵上的应用
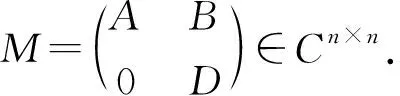
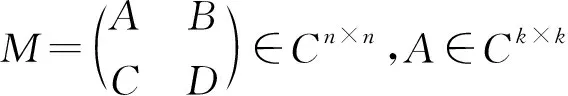



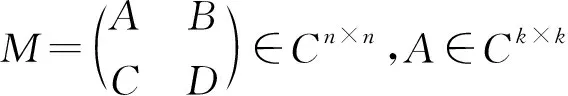


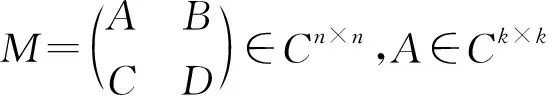


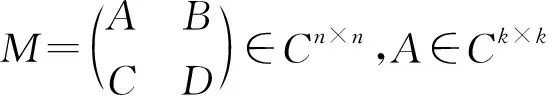
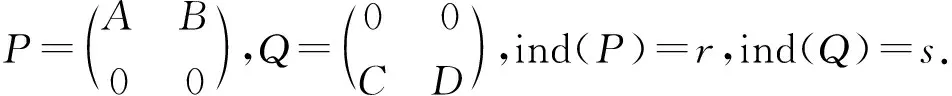

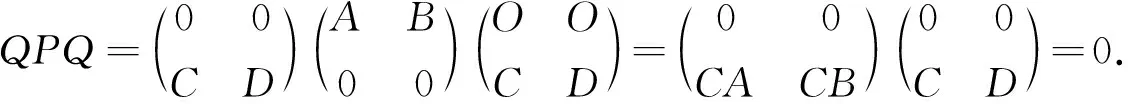
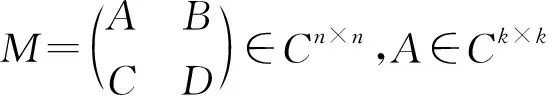
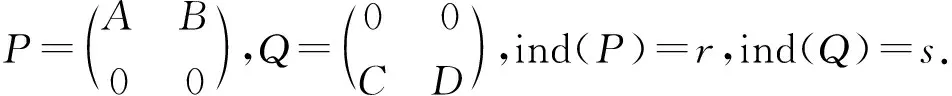
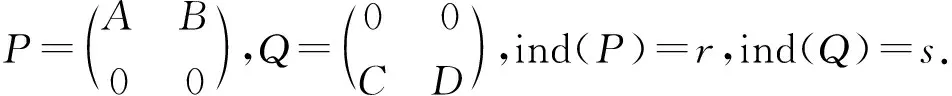
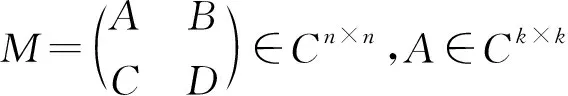
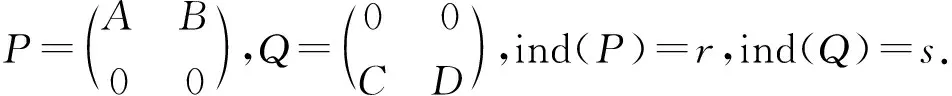
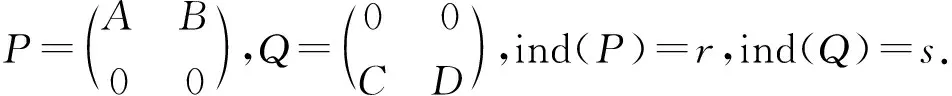
3 例子