《分数的再认识(一)》的教学设计

楼俊民

一、教材内容

北师大版义务教育教科书数学五年级上册第五单元63～64页。

二、教材分析

《分数的再认识（一）》是北师大版五年级上册分数的意义单元的第一课时。在此之前，学生已经初步理解了分数在份数层面的意义，初步感受了分数表示多少的相对性。但是，《分数的再认识（一）》并未脱离从份数角度对分数的理解，强调的还是平均分成几份，取其中的一份，理解的还是整体和部分的关系。所以这一节课是对三年级下册分数初步认识的总结和提升。这堂课的学习目标是概括出分数表示的是整体与部分之间的关系的意义，进一步理解分数表示多少的相對性。

为了丰富对分数的认识，教材安排了三个问题，进一步理解整体与部分的关系。一是对已学的知识进行梳理，整体可以是一个图形，也可以是多个图形，还可以是多组图形。在此基础上，总结分数的意义。整体被平均分成四份，圈出的部分占了三份。整体与部分的关系是一致的。二是从部分出发推测整体，在另一个角度体会整体和部分的关系。部分是一份，整体是四份，这一关系不变。三是分数表示的是整体与部分的关系，整体不同，部分所对应的量也不同，从中体会分数表示多少的相对性。

那么，这堂课除了再认识整体，还可以再认识什么呢？笔者认为，可以再认识“平均”。“平均”一定包含了一样的意思，却不仅仅是一样。一样在什么地方，是形状一样，还是大小一样？是完全一样，或者只是个数相同，这些都反映了学生如何理解平均，都值得深入思考。此外，还可以再认识“一份”，教师需要创设具体的情境，让学生以不同的方式看待一份，从而看到不同的部分和整体之间的关系，体会分数大小相对性的内在联系。

三、教学目标

1.结合具体的情境，通过操作画图等方式，进一步认识“平均分”，“一份”的含义。

2.经历概括分数意义的过程，理解分数表示多少的相对性。

3.在具体的情境中，发展数感，体会数学与生活的密切联系。

四、教学重难点

突出分数意义的建构，通过“一份”联系整体和部分的关系，理解分数大小的相对性。

五、教学预设：

1.情境导入（如图）

这里有一张正方形的纸，现在老师要用它来表示一个分数。请观察课件的演示，说说你在上面找到了什么分数？

你是怎么想的？

生：我找到了3/4，把正方形纸平均分成4份，涂色的占了3份，可以用3/4表示。

生：我看的是空白部分，用1/4表示。因为是把正方形纸平均分成4份，空白的占了1份。

师：如果涂色部分用分数表示，应该是3/4。

【设计意图】  学生学习分数是从折一折、涂一涂开始的。通过这个具体情境，一下子就唤起学生以往学习分数的记忆，进而回顾了分数的份数意义。

2.再认识——“平均分”

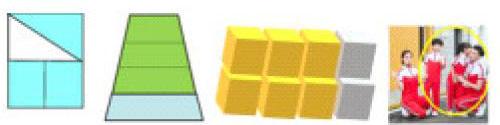
这几个图形，都能用3/4表示吗？

学生讨论：

梯形的大小不同，不是平均分，所以不能用3/4表示。

长方形虽然形状不同，但是面积大小一样，是平均分。

四个人虽然身高、年龄、性别都不相同，但是从个数上看，可以认为是平均分。

立方体是把两个正方体看成一块，它就被分成了四份。

师总结：看来平均的意思不仅仅是形状大小一模一样，可以是大小一样，也可以是个数一样。可以把一个看成一份，还可以把几个看成一份。

【设计意图】学生对“平均”的认识有三个层次。刚开始时，觉得平均分出来的图形的大小和形状必须完全一样;到了第二层次，认识到分出来的图形的大小必须一样，形状可以不同;到了第三层次，他们已经体会到平均可以指的是数量，可以跟大小和形状无关。

3.再认识——“一份”

这里有一幅图，你能把这幅图表示成3/4吗？

生：把3根骨头看成一份，12根骨头就被分成4份，取其中的3份，就是3/4。

师：1根骨头作为一份可以吗？

生：不可以，一根骨头为一份，应该用9/12表示。

师：刚才，我们研究了一些能表示为3/4的图形。你也来设计一个，说说你的想法。

要求说清楚把什么作为整体，多少为一份，取这样的几份。

【设计意图】“一份”介于整体和部分之间，看清了一份，才能看清楚整体和部分的关系。同一个整体，同一个部分，看到不同的一份，就看到了不同的分数。所以，“一份”是理解整体和部分关系的关键。

4.再认识——整体与部分

这里有三盒水彩笔，淘气取出了其中一盒水彩笔的3/4，猜一猜他拿的是哪一盒？（如图）

请你把想法画一画。

学生完成，展示作品。

师：为什么18支的这一盒不可以表示出3/4？

生：因为不能平均分成4份。

师：为什么16支和24支可以表示出3/4？

生：因为它们可以平均分成4份。

从中我们可以发现它们的共同点，你来说一说。

小结：可以表示成形状如上图的，都可以用3/4表示。

但是圈出的部分，为什么数量不一样呢？

生：整体多，取出的部分就多。整体不同，所以取出的部分不同。

师小结：看来，同一个分数，整体不同的时候，取出的部分就不同。分数所表示的具体数量，要考虑整体的大小。

【设计意图】  迪卡说过：“没有任何东西比几何图形更容易印入脑际了，因此用这种方式来表达事物是非常有益的。”在具体的情境中，通过画图这种具象的方式，在具体的数学情境和抽象的数学知识之间构架起桥梁，让学生体会到3/4的本质，也让学生体验到分数大小的相对性，理解到位，落到实处。

5.练习设计

【基础练习】

1.说一说下面每个分数表示的意义。

（1）一张报纸的1/4版面用于广告宣传。

（2）我们班有3/4的男生喜欢打乒乓球。

（3）有专家指出，取消塑料袋无偿供应，全国塑料袋使用量可减少2/3。

学生完成后校对，讲评对错。

2.选一选，对的打√

一根圆棒的1/3知道了，你能知道整体吗？它们之间是什么关系？

3.圈一圈，填一填，再说一说。

【拓展题】

为帮助灾区，奇思捐献了零花钱的1/5，妙想捐献了零花钱的3/5，妙想捐的钱一定比奇思多吗？请说明理由。

学生交流，然后画图表示。

【设计意图】小学生的抽象思维水平不高，而画图比较直观。对于抽象的复杂的题目，通过画图就变得形象简单了，十分符合小学生的思维特点。

最后，通过这节课的学习，说说你对分数有了哪些新的认识？