套管式地埋管换热器热短路及换热性能

李永强，徐拴海，张卫东，孙玉亮，韩永亮，张 浩，黄健丰

(1.煤炭科学研究总院，北京 100013；2.中煤科工集团西安研究院有限公司，陕西 西安 710077)

地热资源作为一种绿色可再生能源，其分布广泛、储量丰富、受外界环境影响小，有望成为人类未来的重要替代能源之一[1-2]。目前，国内开采深层地热能的技术主要有地热尾水回灌技术和地埋管换热技术。地热尾水回灌技术利用压裂技术开采深层地热能，存在地热尾水回灌率低、回灌易堵塞、对地下水环境影响大等不利因素，给地热能的可持续开发利用带来阻碍[3-4]。在此背景下，利用地埋管换热器开采深层地热能成为国内外探索的新方向。地埋管换热器结构为一对同轴套管，其通过套管壁与岩土体热传导和套管内水与管壁之间的对流换热实现“取热不取水”。

近年来随着地热能需求量的增大，针对深井套管式地埋管换热器的研究日益增多，目前多以数值计算为主。R.A.Beier 等[5]在不考虑地层垂向导热的情况下，提出了套管内部流体与周围岩土体之间耦合换热的非稳态解析解，分析了管壁热阻和管内循环水流方向对管内流体温度的影响；H.J.G.Diersch等[6]提出套管式地埋管换热器与岩土体中传热方程，推导并详细描述了有限元求解策略；孔彦龙等[7]基于双连续介质数值模拟法，对单井短期和长期换热量进行评估；卜宪标等[8]在假定内管为绝热情况下，分析了管径、岩土体导热系数、孔深和地温梯度等对采出水温度和换热功率的影响；王硕等[9]建立了管内外全尺寸数值模型，分析了换热量及运行时间对换热器性能的影响；E.Zanchin 等[10]使用COMSOL MULTIPHYSICS 建立二维轴对称模型，分析了管内循环流体流动方向和热短路对孔深为20 m 的套管式地埋管换热器性能的影响；Cheng Wenlong 等[11-13]研究将废弃油井改造为地埋管式地热井，通过建立数学模型分析井深、流速、运行时间等对换热量的影响；王德敬等[14]使用数值模拟方法分析中深层套管式地埋管换热器换热量影响因素，得出换热器内外管之间的热短路是影响其换热性能的不利因素。前人对热短路现象有一些简要介绍，但未深入分析热短路现象及其对换热器性能的影响。

笔者通过建立套管式地埋管换热器与周围岩土体之间的耦合传热模型，分析不同内管壁导热系数和管内循环水流量工况下换热器换热功率和热短路状况，揭示热短路对换热功率的影响，为实际工程设计提供参考。

1 套管式地埋管换热器模型建立

1.1 基本假设

套管式地埋管换热器横截面见图1。套管式地埋管换热器由内管和外管两部分组成；外套管与钻孔壁之间用水泥浆液回填，管内循环水从外管注入，循环水到达井底后从内管反向流出，通过套管壁与周围岩土体进行热交换。

图1 套管式地埋管换热器截面Fig.1 Cross section of coaxial borehole heat exchanger

由于套管式地埋管换热器与周围岩土体之间传热过程复杂，为了建立换热器内水与各区域固体介质之间的非稳态耦合传热模型，现对该物理问题作如下假设：

①岩土体为半无限大各向同性介质，物性参数为定值；

② 固井水泥、水、套管热物性参数不随温度变化；

③忽略外套管的热容量，且不考虑套管的垂向导热；

④ 管内同一截面上水温、流速均匀一致；

⑤ 忽略地下水渗流对岩体传热的影响；

⑥ 忽略大气环境对地表温度的影响，将地表温度看作恒定值。

1.2 数学模型

1.2.1 固体区域导热方程

固体区域导热方程如下：

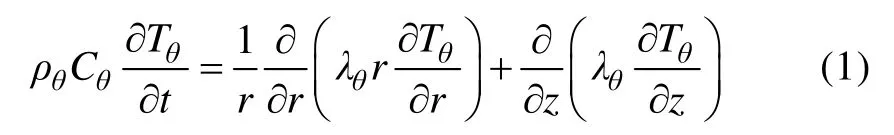
式中ρ为密度，kg/m3；C为比热容，J/(kg·K)；T为温度，K；λ为导热系数，W/(m·K)；r为距钻孔轴线距离，m；t为时间，s；z为距地表距离，m；θ可表示为s、g、pi，其中s 表示岩土体，g 表示固井水泥，pi 表示内管。

1.2.2 外管能量守恒方程

外管能量守恒方程如下：

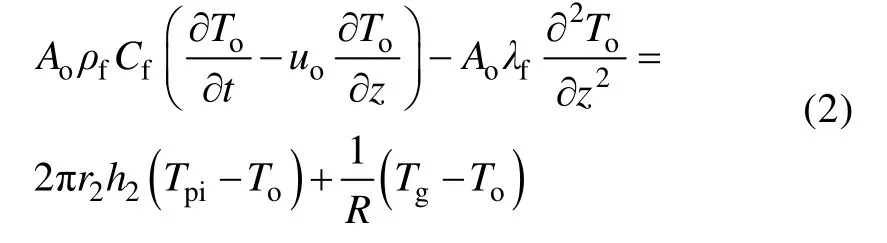
式中To为外管水的温度，K；Ao为外管过水断面积，m2；ρf为水的密度，kg/m3；Cf为水的比热容，J/(kg·K)；uo为外管中水的流速，m/s；λf为水的导热系数，W/(m·K)；r2为内管半径，m；h2为内管外壁对流换热系数，W/(m2·K)；R为单位长度热阻，(m·K)/W。

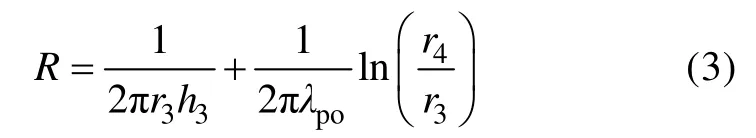
式中h3为外管壁对流换热系数，W/(m2·K)；r4为外管半径，m；r3=r4–bpo，bpo为外管壁厚，m；λpo为外管导热系数，W/(m·K)。

1.2.3 内管能量守恒方程

内管能量守恒方程如下：

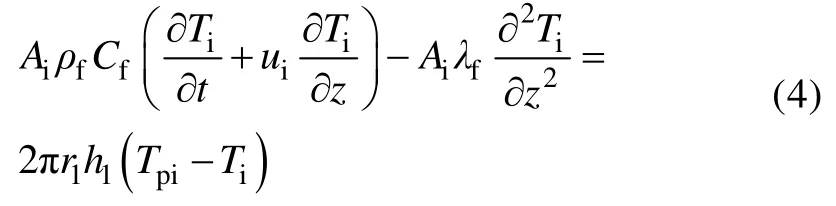
式中Ti为内管水的温度，K；Ai为内管过水断面积，m2；h1为内管内壁对流换热系数，W/(m2·K)；ui为内管中水的流速，m/s；r1=r2-bpi，bpi为内管壁厚，m。

1.3 边界条件

因套管换热器与岩土体进行热交换时，岩土体温度受影响的范围有限，因此，将距钻孔足够远处设为恒温边界。固井水泥中流出的能量等于外管中水吸收的能量，可知固井水泥与外管循环水之间边界条件为：

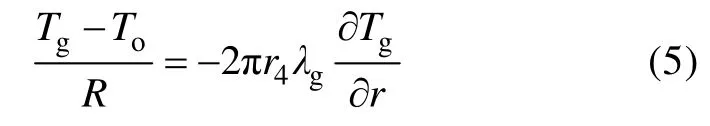
内管内壁对流换热边界条件为：

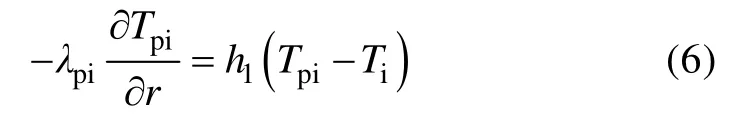
内管外壁对流换热边界条件为：

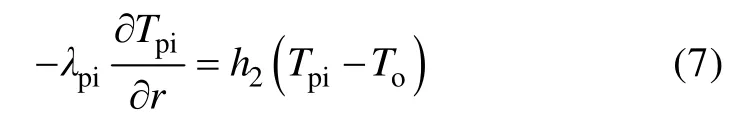
固井水泥与岩土体之间的接触传热边界条件为：

当Z=H时，

外管顶部注入水的温度为：

1.4 初始条件

假设内管和外管中水的初始温度沿钻孔深度方向与周围岩土体的初始温度相同。地温梯度为0.03 K/m，地表温度为289.15 K，则岩土体中初始温度为：

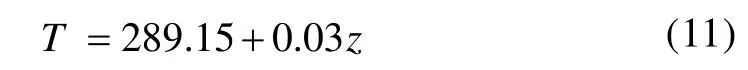
式中z为岩土体距地面的距离，m。

1.5 对流换热系数

管内对流换热系数Nu使用Gnielinski 公式[15]计算，公式如下：

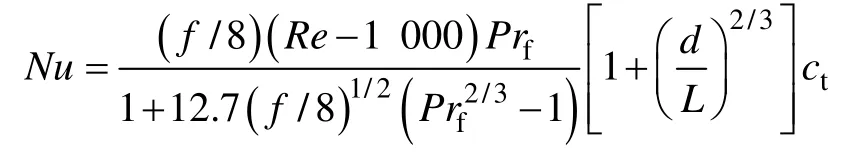
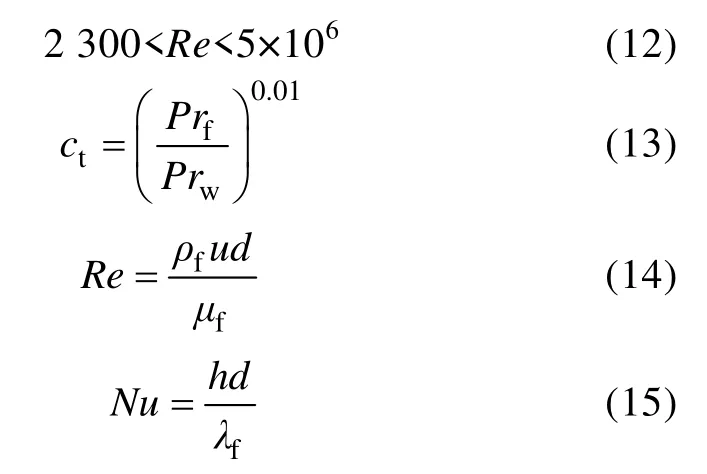
式中Pr为普朗特数，下标f、w 分别表示以水和壁面温度来计算水的普朗特数；d为管道的当量直径，m，对于内管d=2r1，对于外管d=2(r3–r2)；L为管的长度，m；Re为雷诺数；u为水的流速，m/s；μf为水的动力黏度，Pa·s；f为管内湍流流动的阻力系数，用Filonenko 公式[15]计算：

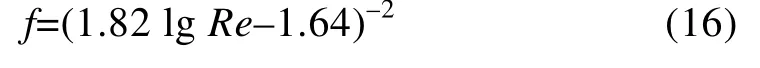
2 参数设定与计算方法

本文采用常用的套管式地埋管换热器参数建模，模型所用参数见表1。考虑中国北方冬季供暖期一般为4 个月，以一个月30 d 计，每个供暖期总供暖时间为120 d。使用COMSOL MULTIPHYSICS求解上述偏微分方程组，分析投入运行后的第一个供暖期取热情况。

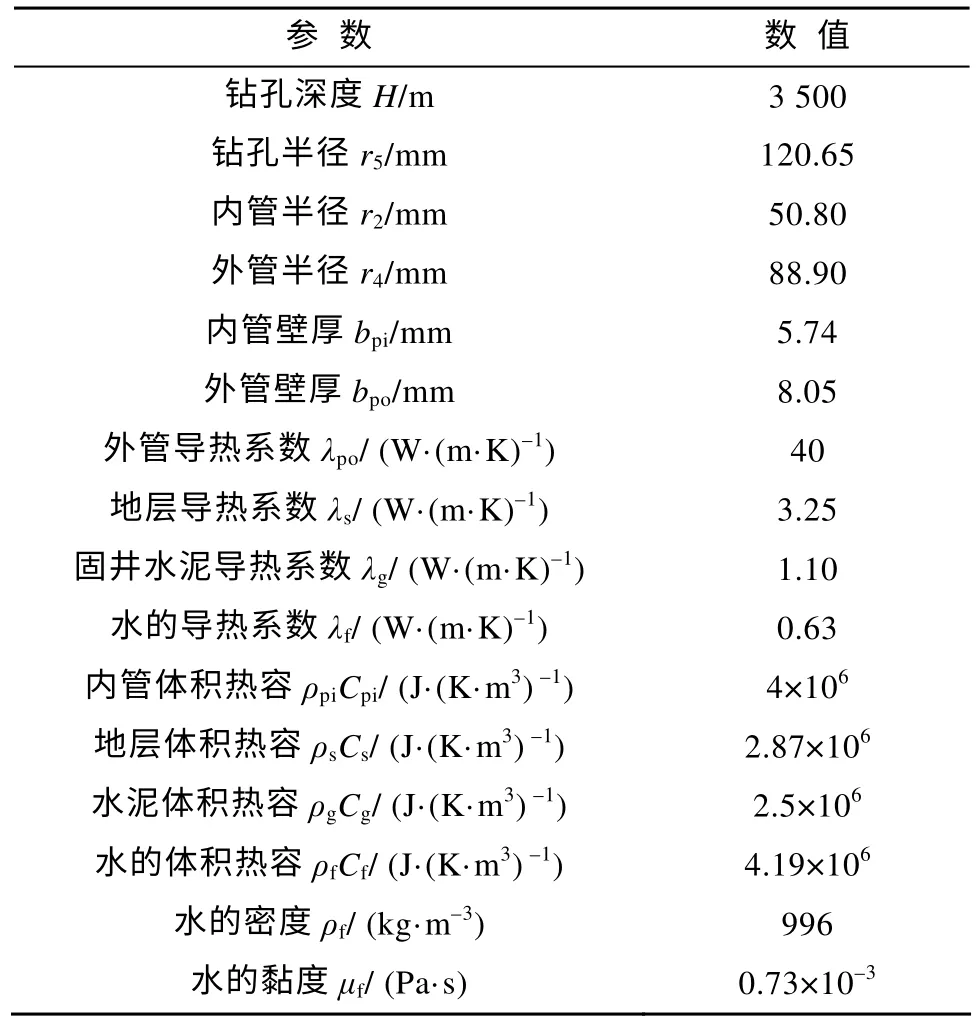
表1 换热器相关参数Teble 1 Parameters of heat exchanger

3 模型验证

为了验证模型计算结果可靠性，采用开源模拟软件OpenGeoSys(OGS)[7,16]中双连续介质法地埋管模块与本文模型对比。取内管导热系数为0.2 W/(m·K)，循环水流量为18.9 m3/h，其他参数同表1。得到连续运行120 d 两种方法计算出水温度随时间的变化，如图2 所示。由图2 可知，两种方法所得出水温度值非常接近，且两者差值随时间增长逐渐减小。运行第0 d、20 d、120 d 时两者差值分别为1.24℃、0.36℃、0.09℃。由此可知，本文所建模型较为可靠。

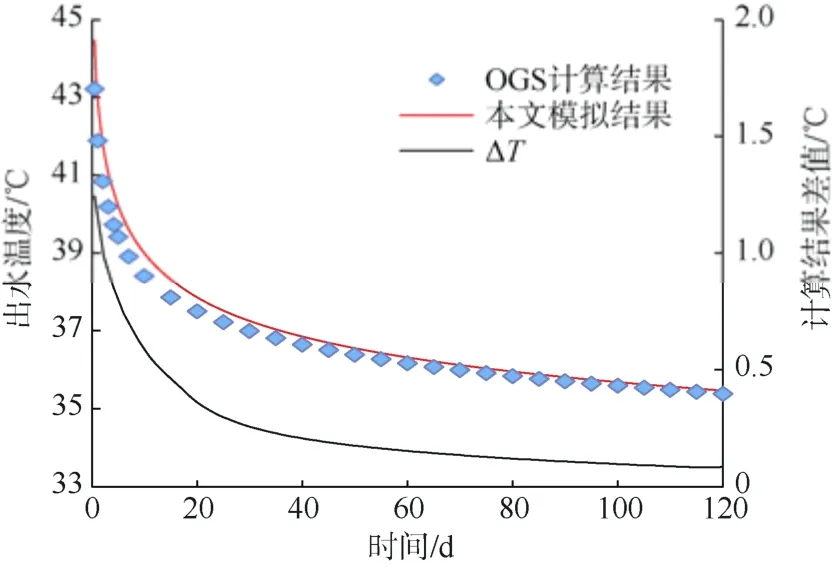
图2 出水温度计算结果对比Fig.2 Comparison of calculation results of outflow temperature

4 分析和讨论

为了评估套管式地埋管换热器热短路现象，引入换热器效能η[17]作为衡量指标，其表达式见式(17)。换热器效能η为套管式换热器实际换热量和最大换热量之比，其中最大换热量是假设内管壁导热系数为0，内外管之间不存在热干扰时得到的换热量。换热器效能越小，热短路损失越大，此时热短路现象也越明显。

式中vf为套管换热器内水的流量，m3/s。

4.1 内管导热系数的影响

取内管导热系数λpi为0(绝热管)、0.1、0.3、0.5、1 W/(m·K)等一系列数值，管内循环水流量为25 m3/h，得到连续运行120 d 出口水温随时间变化关系(图3)。由图3 可知，出口水温随时间增长逐渐降低；在初始运行阶段出口水温下降幅度最大，然后逐渐趋于平缓；内管导热系数越小，初始运行阶段出口水温下降幅度越大。这是由于在初始阶段岩体温度场未受扰动，岩体温度较高，水从岩体中吸收的热量多。随着时间的增长，靠近钻孔壁处岩体逐渐冷却；由于岩体导热系数较低，远处的热量来不及传到钻孔壁，造成钻孔壁冷堆积，水从岩体中吸收的热量减少，致使出口水温下降快。出口水温随内管导热系数的增大而降低，当内管为绝热管时出口水温最高。内管导热系数分别为0、0.1、0.3、0.5、1 W/(m·K)时，对应的连续运行120 d 出口水温平均值分别为40.48℃、36.24℃、30.77℃、27.63℃、23.67℃。内管导热系数为1 W/(m·K)时出口水温平均值较内管为绝热管时降低16.81℃。由此可见，内管导热系数对出口水温影响显著，内管应尽量选择导热系数小的管材。

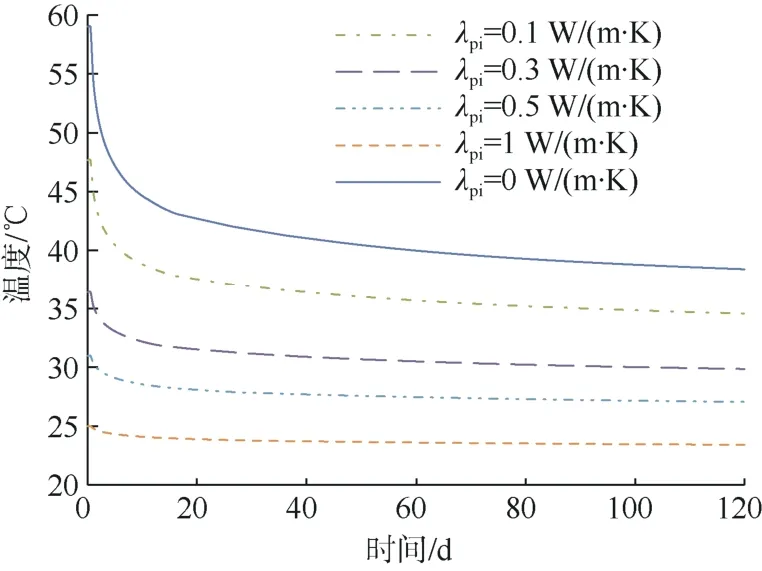
图3 出口水温随时间的变化Fig.3 Variation of outflow temperature with time

图4 为连续运行120 d 后内外管中水温沿垂向分布图。由图4 可知，内管为绝热管时孔底部温度即为出口水温。随着内管导热系数的增加，孔底部温度逐渐升高，而出口水温逐渐降低，这是由于内管为绝热管时，内外管中的水不发生热交换，内管水温在流动过程中不会发生改变；当内管不是绝热管时，内外管中的水通过内管管壁对流换热，发生热短路现象。由于内管水温较高，内管水在向上流动过程中热量不断通过管壁传向外管，致使内管水温沿流动方向逐渐降低。外管水向下流动过程中，吸收了来自内管壁和钻孔孔壁的热量，水温逐渐升高。内管管壁导热系数越高，外管从内管中吸收的热量就越多，内外管中水的温差也就越小。外管水温升高进而又使内管回水温度升高。所以内外管中水的平均温度随内管壁导热系数的增大而增大。由于热短路的影响，套管中产生热堆积，外管水温的升高导致其与地层岩土体的温差降低。由热流密度公式q=ΔT/R可知，温差越小水从岩土体中吸收的热量也就越少。

表2 给出了连续运行120 d 平均换热功率与内管壁导热系数的对应关系，可知随内管导热系数增大，换热器的换热功率降低，换热器效能降低，热短路现象表现越显著。综上所述，热短路使管内发生热堆积，降低了换热器的换热功率。

4.2 管内循环水流量的影响

分别取内管导热系数λpi为0 W/(m·K)、0.3 W/(m·K)，循环水流量在10～40 m3/h 范围内取8 个值，管内循环水为外进内出的工况下连续运行120 d，得到平均换热功率和平均出口水温与循环水流量的关系(图5)。

当内管导热系数为0 时，内外管之间不发生热短路现象。由图5 可知，此时随着循环水流量增大，平均换热功率逐渐增大，但其增幅逐渐降低；出口平均水温随循环水流量的增加而降低。循环水流量从10 m3/h 增加到40 m3/h，平均换热功率增加了218 kW，出口平均水温从65.4℃下降到32.3℃。这是由于流量增大时，外管循环水与外管壁之间的对流换热更加强烈，单位时间内循环水从岩体中获取的总热量增加。但流量增加后，管内循环水与管壁接触的时间变短，单位体积水获得的热量降低，导致水温随流量增大而降低。

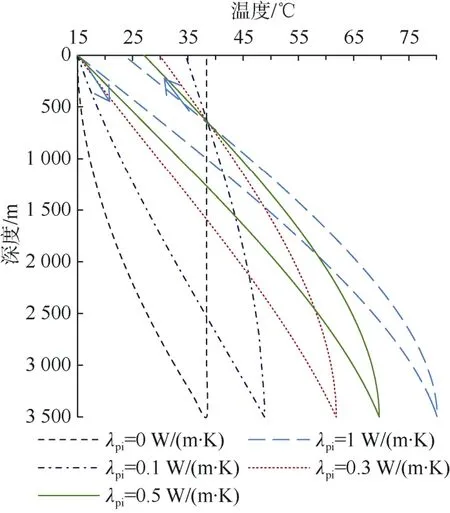
图4 运行120 d 后管内水温沿垂向分布Fig.4 Vertical distribution of circulating water operation of temperature after 120 days

表2 连续运行120 d 平均换热功率和换热效能与内管壁导热系数的对应关系Table 2 Mean heat transfer power and heat transfer efficiency corresponding to with the thermal conductivity of the inner tube after continuous operation for 120 days

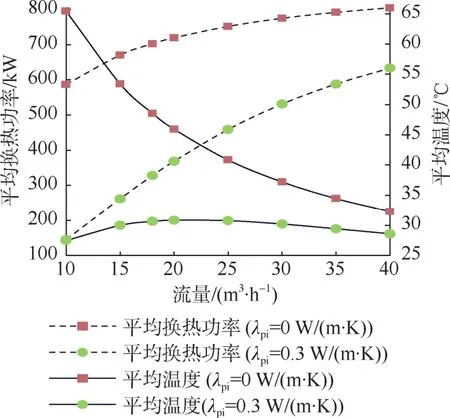
图5 平均出口水温和平均换热功率随流量的变化Fig.5 Variation of average outflow temperature and average heat transfer power with water flow

当内管导热系数为0.3 W/(m·K)时，内外管之间发生热短路现象。由图5 可知，出口平均水温随循环水流量的增加先增大后降低，平均换热功率随循环水流量的增大而增大。循环水流量从10 m3/h 增加到40 m3/h，平均换热功率增加488.1 kW，出口平均水温最大值与最小值之差为3.83℃。

图6 显示换热器效能与循环水流量的相关关系。循环水流量为10 m3/h 时，换热器效能为24.7%，此时热短路现象显著。随流量的增大换热器效能增大，热短路现象逐渐减弱。当循环水流量增大到40 m3/h 时，换热器效能为78.7%；热短路对换热器换热性能影响随循环水流量增大逐渐降低。当流量较小时，循环水在管内停留时间长，有利于单位体积外管循环水从岩体中吸收更多的热量，但此时热短路损失大，内外管循环水温差较小，导致出口平均水温较低。随流量增大，外管循环水从岩体中吸收的热量增多，热短路损失降低，出口平均水温略有升高；流量持续增大，单位体积水获得的热量减少，出口水温下降。

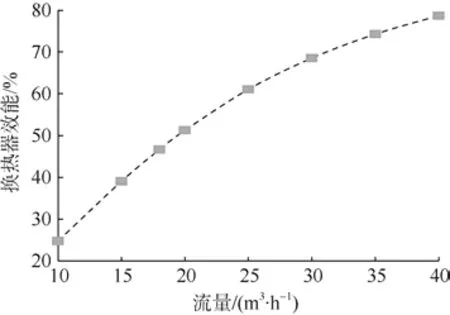
图6 换热器效能随流量的变化Fig.6 Variation of heat exchanger efficiency with water flow

由以上分析可知，无论内外管之间是否存在热短路，平均换热功率均随循环水流量增大而增大，热短路现象随循环水流量增大而减弱。

5 结论

a.出口水温在初始运行阶段下降显著，随着时间的增长，出口水温趋于稳定。内管导热系数越大，出口平均水温越低；在套管式地埋管换热器设计时应选择导热系数较低的内管，以提高换热器换热功率。

b.内管导热系数越大，热短路现象越明显。热短路使内外管中循环水温差降低，管内出现热堆积，导致换热器换热功率降低。

c.在不同循环水流量条件下，套管式地埋管换热器的换热功率随循环水流量的增大逐渐增大。当内外管之间不存在热短路时，随循环水流量增大，出口水温下降显著。内外管之间存在热短路时，随循环水流量增大出口水温先升高后降低，其变化幅度较小，随着流量增大，换热器效能增大，热短路现象减弱。