基于LedaFlow和Fluent的冲蚀临界速率研究

昝林峰 孙小喆 李晓平 洪炳沅 李彦博 杨静 宫敬

1.中国石油工程建设有限公司西南分公司2.中国石油大学(北京)油气管道输送安全国家工程实验室/石油工程教育部重点实验室/城市油气输配技术北京市重点实验室

页岩气属于非常规天然气，2011年国土资源部发布公告将页岩气作为新的独立矿种予以管理[1]。近年来，水平井技术和压裂技术(多层压裂、清水压裂、重复压裂及同步压裂)的长足进步有效地促进了页岩气的大规模开发[2-4]。在气田开采初期，流量较大，速度较快，对于出砂问题，通常是在地面系统中增加除砂器进行除砂[5]，除砂器一般设在采气树的井口一级节流阀后[6]。由于页岩气加砂量巨大，即使仅有少量的砂通过除砂器后进行后续流程，长时间也会造成较大影响，对管壁尤其弯头部位造成冲击磨损，使得管壁结构磨损后无法承担管内压力，引起管道失效，造成生产事故[7]。

冲蚀研究主要针对冲蚀临界速率和冲蚀损失率，从经验半经验模型到理论模型，如今依然在不断修正，并且应用CFD进行更多的研究。美国石油组织API最早提出了最为广泛使用的冲蚀临界速率预测方法[8-9]。后来一些研究者对API模型的冲蚀临界速率进行了修正，如Swedeman和Arnold[10]提出弯头、T型三通在不同输砂率条件下冲蚀临界速率的估算方法；Salama[11]在Swedeman和Arnold算法的基础上，考虑了流体密度对冲蚀临界速率的影响；Jordan[12]引入了阻滞区概念，通过反复迭代运算求解多相流管线中的油气冲蚀临界速率。目前，关于冲蚀临界速率和冲蚀损失量关联的研究比较少。

本研究基于LedaFlow的冲蚀模块对页岩气携砂能力进行模拟计算，分析了管道直径、压力和流量对冲蚀临界速率的影响；并通过Fluent软件对临界速率下管道的壁面最大冲蚀损失量进行数值模拟计算，得到了冲蚀临界速率与管道壁面最大年损失量之间的关系，为生产运营提出建议。

1 管道冲蚀临界速率计算

1.1 LedaFlow冲蚀临界速率计算模型

冲蚀临界速率是指流体不发生冲蚀的最高流速，当流体流速高于这一临界值时，会发生冲蚀。这类模型在指导工程实际中发挥了重要的作用。LedaFlow基于以下API RP 14E模型(式1)进行冲蚀计算[8-9]。

(1)

式中：Ve表示冲蚀临界速度，m/s；C为经验系数，m/s(kg/m3)0.5，建议取值100～200。当流体为无砂且无腐蚀现象的流体，连续工况下C可以取值100，间歇工况可取125，对于含砂情况应根据详情适当降低C值；ρm为流体在流动条件下的混合密度，kg/m3。

冲蚀判断准则如式(2)及式(3)。

EVR=Vmix/Ve

(2)

Vmix=Usliq+Usgas

(3)

式中：EVR(Erosional Velocity Ratio)代表冲蚀比，是混合流体流速和冲蚀临界速率的比值。当EVR<1时，不发生冲蚀；Vmix为流体的混合速度，m/s；Usliq为液相折算速度，m/s；Usgas为气相折算速度，m/s。

1.2 冲蚀临界速率影响因素分析

根据API计算模型公式，选择对流量、管道内径和管道出口压力影响冲蚀临界速率的因素进行分析。由于API模型没有考虑含砂率的影响，故不进行分析。本节的初始模型设置为1 km管道，出口压力10 MPa，内径28 mm，壁厚4.5 mm，管壁粗糙度0.05 mm，起点温度60 ℃，输送气体流量1.2 kg/s，含砂率为0.05。

1.2.1 气体流量影响

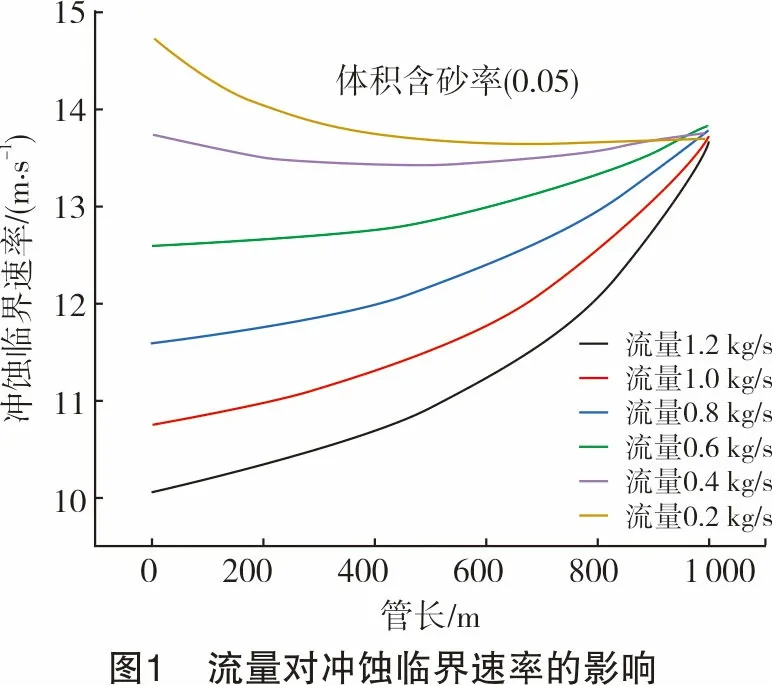
由软件内置模型可知，模型没有考虑颗粒粒径的影响，即所有粒径下的计算结果均相同。因此，在初始模型的条件下，改变流量大小(1.2～0.2 kg/s)，观察流量对冲蚀临界速率的影响情况。

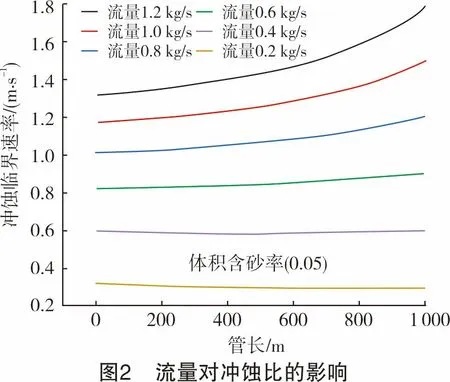
从图1可知，随着流量减小，冲蚀临界速率增大。从图2可知，冲蚀比随着流量增大而增大，故在管径一定的情况下，流量越大越容易发生冲蚀。在初始模型的条件下，当流量增大到0.8 kg/s以上时，冲蚀比大于1，有发生冲蚀的风险。随着流量增大，管道沿线冲蚀临界速率逐渐增大，冲蚀比最高点为终点，故最容易发生冲蚀的位置在终点；由于实际流体流速沿管线的变化没有冲蚀临界速率大，随着流量减小，起点的冲蚀临界速率增大，最易发生冲蚀的位置向前移。

1.2.2 管道内径影响

如图2所示，在流量为1.2 kg/s的条件下，最容易发生冲蚀的位置是终点位置。因此，选择终点位置作为冲蚀临界速率的观察点。在其他初始条件不变的情况下，通过改变内径从而改变管道的横截面积，观察内径对冲蚀临界速率的影响。

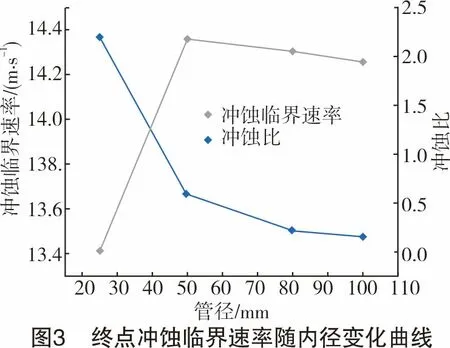
由图3可知，在流量相同的情况下，终点冲蚀临界速率随内径的增大，先增大后减小，但是冲蚀比随内径增大而不断减小。因此，在其他条件相同的情况下，内径越小越容易发生冲蚀。

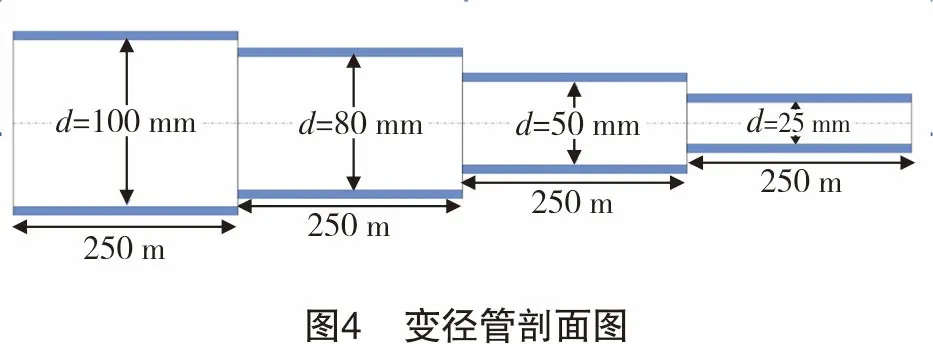
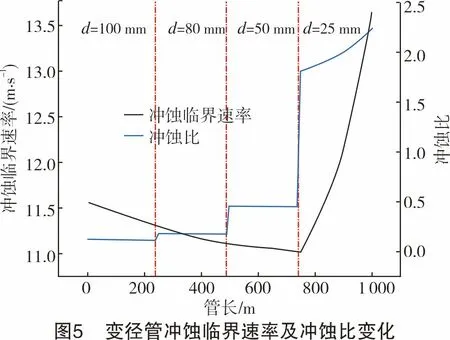
对于变径管，内径逐渐变小(如图4所示)，模拟结果如图5所示。

从图5可知，随着内径减小，冲蚀比逐渐增大，也就是越容易发生冲蚀。所以，对于变径管，要优先考虑内径小的管径。

1.2.3 出口压力影响

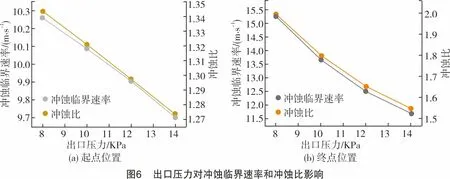
其他条件与初始模型相同，计算模型为组分模型，出口压力影响全管线的压力，通过改变出口压力，观察冲蚀临界速率的变化趋势。由图1可知，在流量为1.2 kg/s的条件下，从起点位置到终点位置，冲蚀比不断增大。因此，选取起点和终点位置观察压力对冲蚀临界速率的影响即可代表压力对全管线冲蚀的影响。

从图6可知，在流量、内径等其他条件相同的情况下，在一定压力变化范围内，出口压力越大，起点和终点冲蚀临界速率越小，冲蚀比也越小，越不容易发生冲蚀。

2 冲蚀临界速率下的壁面冲蚀损失分析

2.1 Fluent冲蚀数值模拟

LedaFlow软件虽然能通过API 14E RP模型计算出冲蚀临界速率，然后基于冲蚀比简便地判断是否发生冲蚀，但无法计算出具体的管壁冲蚀损失量，也没有考虑粒径、含砂率等因素的影响。因此，通过Fluent模拟冲蚀临界速率对应的冲蚀损失，从而对该方法进行补充。

通过LedaFlow对3组管径(50 mm、80 mm和100 mm)进行压力、气体流量、含砂率的输送模拟，得到了不同条件下的冲蚀临界速率，然后通过Fluent数值模拟得到3组颗粒(50 μm、200 μm和300 μm)在该

冲蚀临界速率下的管壁最大年冲蚀损失量。在数值模拟中，选用生产中冲蚀严重的90°弯管进行研究[13]。

2.2 管壁冲蚀损失数值模拟结果分析

2.2.1 不同管径下的壁面最大年冲蚀损失量

Fluent计算出的最大冲蚀率的单位为kg/(m2·s)，该值除以管道钢材的密度可以得到单位时间内颗粒造成的管壁厚度损失ER(m/s)[14]。本研究将其转化为管壁最大年冲蚀损失量π1( mm/a)，如式(4)。

π1=ER×3 600×24×365×1 000

(4)

选取管道在模拟的输送条件下不同位置的冲蚀临界速率和此时的颗粒质量流量，通过Fluent数值模拟得到在该临界速率下管道最大的管壁年冲蚀损失量π1。80 mm管径的计算结果如图7所示。

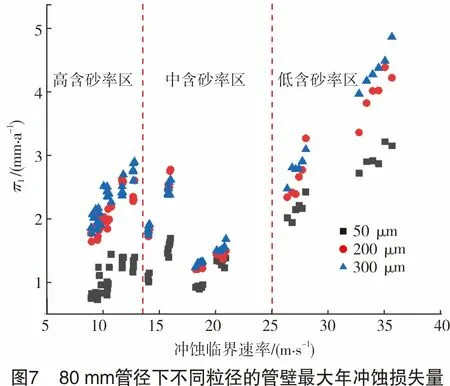
从图7可知，整体上看，在粒径为50～300 μm时，相同的冲蚀临界速率计算出的管壁最大年冲蚀损失量π1与颗粒粒径有关，颗粒粒径越大，π1越高。

由于50 mm管径的压降比较大，在生产末期(低含砂率区)设计的工况管道起点压力小于8 MPa，此时会出现负压，工况不成立，故对于50 mm管径没有低含砂率区的数据。图8表示的是200 μm粒径在不同管径下的计算结果。

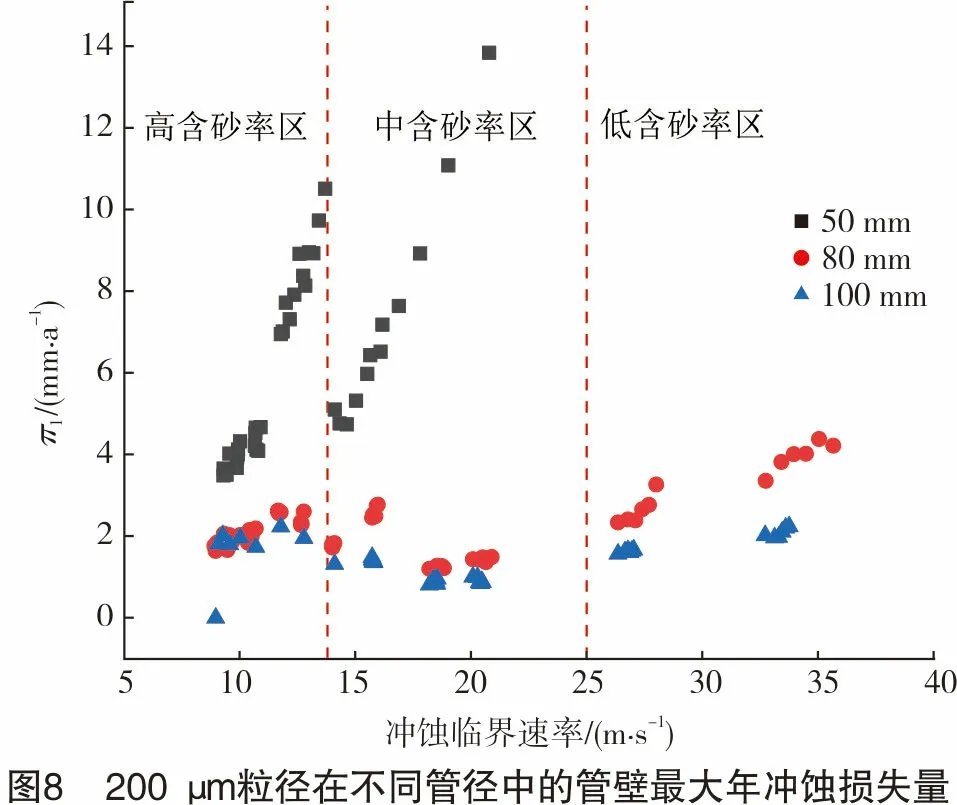
从图8可知：50 mm管径的管壁最大年冲蚀损失量π1明显大于相同冲蚀临界速率下80 mm和100 mm管径下的结果；随着临界速率的增大，80 mm管径的π1也明显大于100 mm管径下的结果。因此，对于相同直径的颗粒，管径越小，管壁最大年冲蚀损失量越大。

2.2.2 冲蚀临界速率与π1关系曲线修正

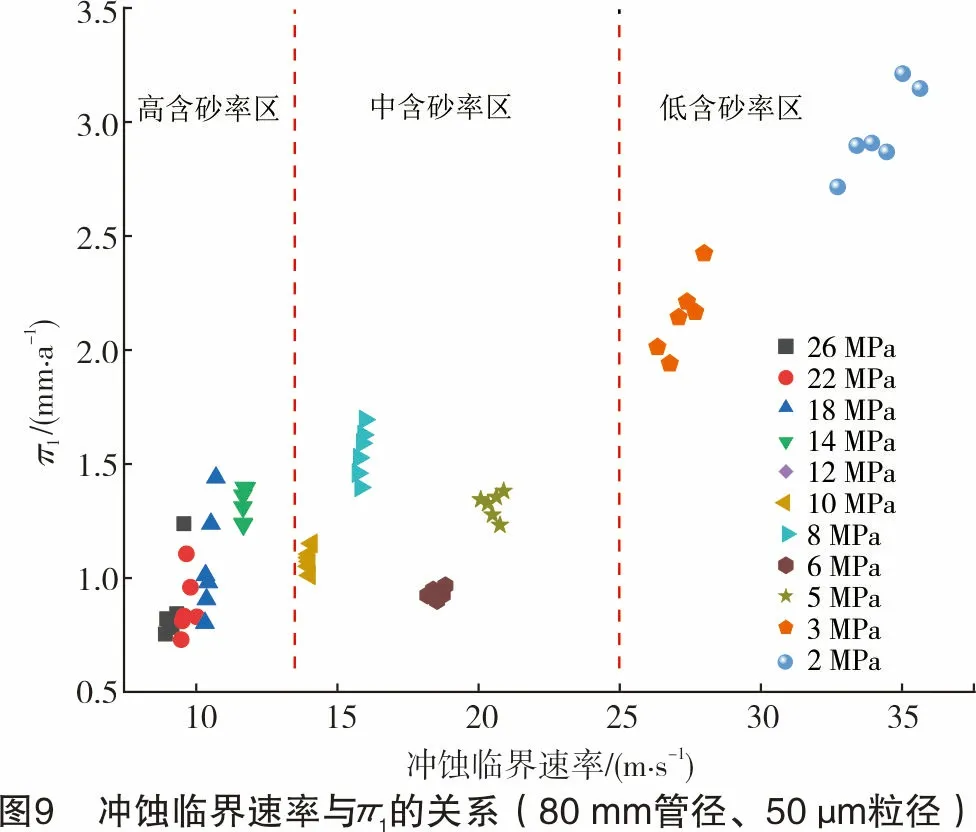
将图7中50 μm粒径的数据单独绘制为如图9。从图9可以看出，在相同压力条件下，π1与冲蚀临界速率表现为正比例关系，即冲蚀临界速率越大，管壁最大年冲蚀损失量越大。

但是对于不同压力条件和含砂率，规律不明显。针对压力、质量含砂率等变量对数据进行初次修正，将同一管径、同一粒径下的数据修正为指数函数关系。随后针对管径和颗粒的粒径进一步对数据进行修正[15]，如式(5)。

(5)

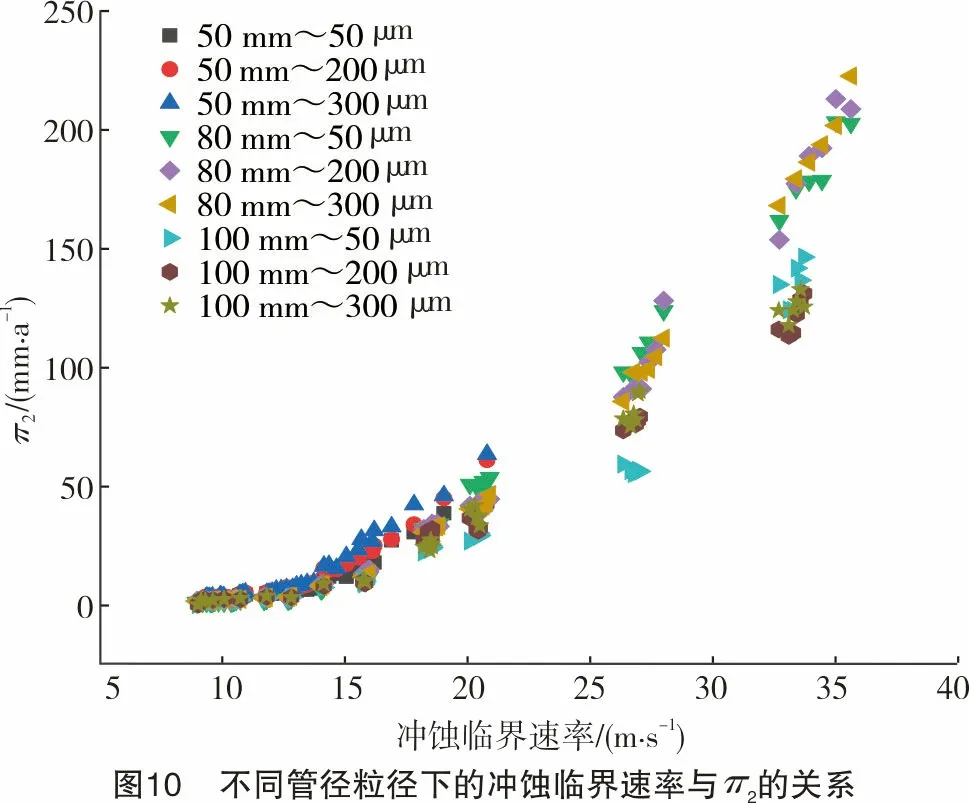
修正后结果如图10所示。

最终得到管壁最大年冲蚀损失量计算公式,见式 (6)。

(6)

式中：P为实际压力， MPa；P0为参照压力， MPa，本研究取26 MPa；r为实际颗粒质量含砂率；r0为参照颗粒质量含砂率，本研究取0.001 26；d为管道内径， mm；d0为参照管道内径， mm，本研究取100 mm；dp0

为参照颗粒粒径， mm，本研究取300 μm；dp为颗粒粒径， mm。

上式中压力的指数(0.5)和质量含砂率的指数(1.5)是根据理想气体状态方程推导出压力、质量含砂率和冲蚀临界速率Ve的关系得到的。颗粒粒径的指数(-0.2)是根据Fluent中的通用冲蚀模型得到的。

根据式(6)，可以直接通过冲蚀临界速率计算出管壁最大年冲蚀损失量，避免了Fluent计算时间太长的问题，完善了LedaFlow中的API冲蚀计算模型。

2.2.3 公式验证

对式(6)进行验证。选取LedaFlow计算出的其他几组数据，根据式(6)计算出管壁最大年冲蚀损失量，与Fluent数值模拟的结果进行对比。结果如表1所示。

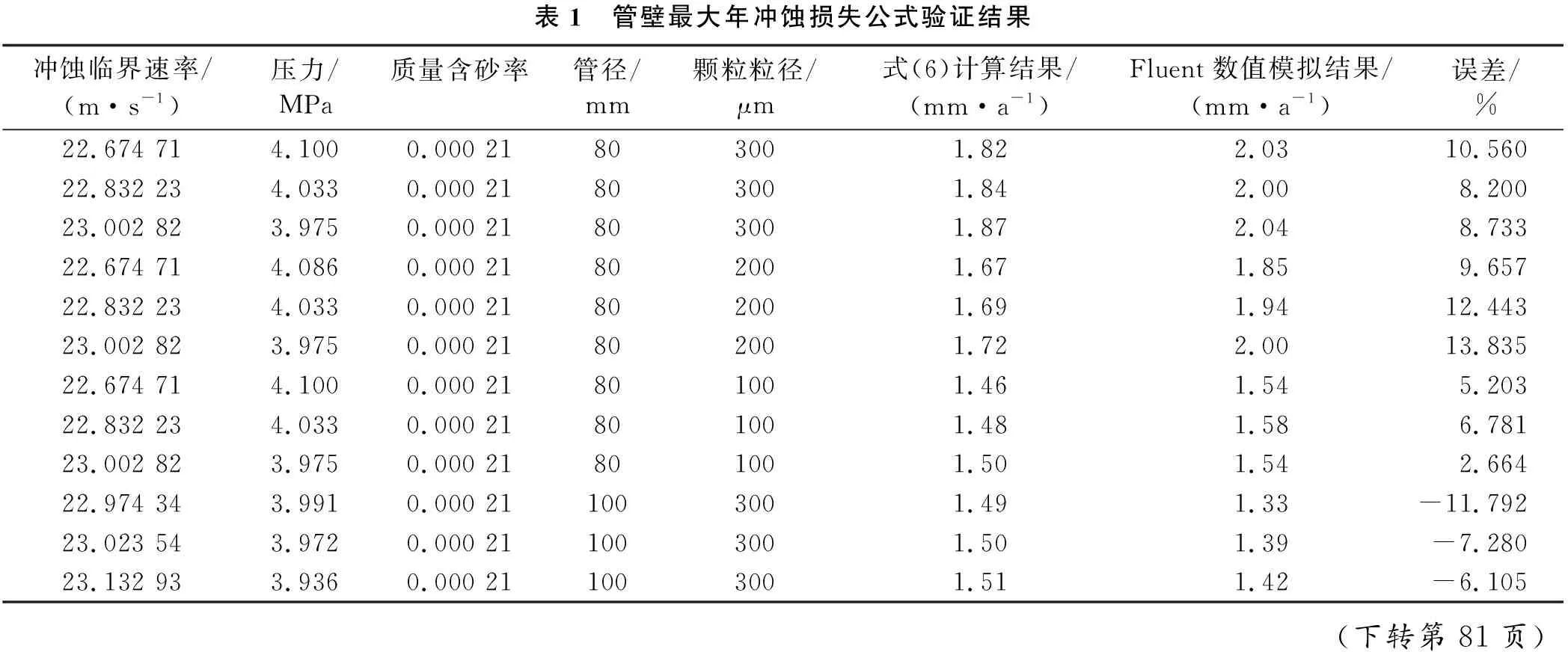
表1 管壁最大年冲蚀损失公式验证结果冲蚀临界速率/(m·s-1)压力/MPa质量含砂率管径/mm颗粒粒径/μm式(6)计算结果/(mm·a-1)Fluent数值模拟结果/(mm·a-1)误差/%22.674 714.1000.000 21803001.822.0310.56022.832 234.0330.000 21803001.842.008.20023.002 823.9750.000 21803001.872.048.73322.674 714.0860.000 21802001.671.859.65722.832 234.0330.000 21802001.691.9412.44323.002 823.9750.000 21802001.722.0013.83522.674 714.1000.000 21801001.461.545.20322.832 234.0330.000 21801001.481.586.78123.002 823.9750.000 21801001.501.542.66422.974 343.9910.000 211003001.491.33-11.79223.023 543.9720.000 211003001.501.39-7.28023.132 933.9360.000 211003001.511.42-6.105

从表1可以看出，公式计算出的结果与数值模拟的结果，最小误差为2.664%，最大误差为13.835%，平均误差为9.809%。误差较小，模型较准确。

3 结论

(1) 通过LedaFlow软件的模拟可知，在API RP 14E模型中影响冲蚀临界速率的因素包括流量、管径和出口压力。整体上看，流量增大，冲蚀临界速率减小，但是冲蚀比增大，故容易发生冲蚀；管道内径和出口压力增大，冲蚀比减小，不容易发生冲蚀。

(2) 冲蚀临界速率对应的管壁最大年冲蚀损失量与颗粒粒径和管径有关，对于相同的冲蚀临界速率，在其他流动参数均相同的情况下，对于50～300 μm的颗粒，粒径越大，管壁最大年冲蚀损失量越大；管径越小，管壁最大年冲蚀损失量越大。

(3) 经过修正，得到了冲蚀临界速率和管壁最大年冲蚀损失量的关系，可根据式(6)在已知冲蚀临界速率的情况下，计算出管壁最大年冲蚀损失量，从而设计合理的管壁厚度以及管道使用年限。