判断函数凸性的若干方法
2020-04-16吴菁菁朱永贵
吴菁菁,朱永贵
(中国传媒大学数据科学与智能媒体学院,北京100024)
1 引言
凸函数是一类基本函数,具有非常好的分析学性质,在极值研究、不等式证明、数学规划、逼近论、变分学、最优控制理论、对策论等领域有着广泛的应用。本文介绍了判断多元二次函数凸性的方法。
2 基本概念
定义1.2.1 凸函数:设函数f:D⊂Rn→R,其中D为凸集,对任意的x,y∈D及任意的实数λ∈[0,1]都有f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y),称f为D上的凸函数。
定义1.2.2 严格凸函数:设函数f:D⊂Rn→R,其中D为凸集,对任意的x,y∈D,x≠y及任意的实数λ∈[0,1]都有f(λx+(1-λ)y)<λf(x)+(1-λ)f(y),称f为D上的严格凸函数。
3 定理
定理1.3.1 设f在凸集D⊂Rn上一阶连续可微,则f在D上为凸函数的充要条件是f(x)≥f(x*)+∇f(x*)T(x-x*),∀x*,x∈D
证明:
必要性:设f(x)为凸函数,根据凸函数的定义,对任意的x*,x∈S及每个数λ∈(0,1),有f(λx+(1-λ)x*)≤λf(x)+(1-λ)f(x*)
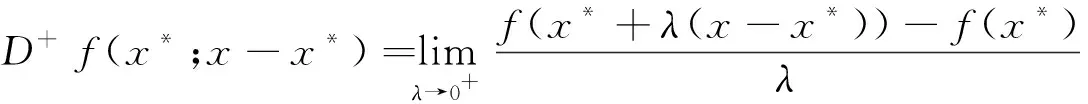
从而得出D+f(x*;x-x*)≤f(x)-f(x*)
由于f(x)可微,根据上述式子,则有∇f(x*)T(x-x*)≤f(x)-f(x*)
即f(x)≥f(x*)+∇f(x*)T(x-x*)
充分性:设对任意的x*,x∈S,有f(x)≥f(x*)+∇f(x*)T(x-x*),令y是x*与x连线上某一点,即对某一个λ∈(0,1),有y=λx+(1-λ)x*。由于S为凸集,则y∈S,根据假设,对于点x*,x,y∈S,下列两式成立:
f(x*)≥f(y)+∇f(y)T(x*-y),f(x)≥f(y)+∇f(y)T(x-y),合并化简得到:
(1-λ)f(x*)+λf(x)≥f(y)+∇f(y)T[(1-λ)(x*-y)+λ(x-y)]
=f(y)+∇f(y)T[λx+(1-λ)x*-y]
=f(y)
即f(y)≤λf(x)+(1-λ)f(x*)
上式即f(λx+(1-λ)x*)≤λf(x)+(1-λ)f(x*)
由凸函数的定义知f(x)是凸函数。[2]
定理1.3.2 设f在凸集D⊂Rn上一阶连续可微,则f在D上为严格凸函数的充要条件是当x≠y时成立f(x)>f(x*)+∇f(x*)T(x-x*),∀x*,x∈D
证明:
必要条件:设f(x)是严格凸函数,自然f(x)也是凸函数,对于任意两个不同点x*,x∈S,
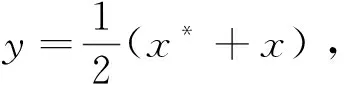
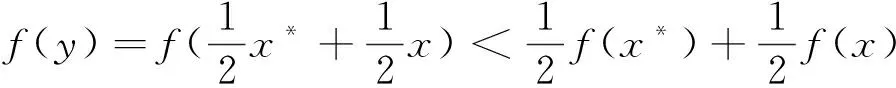

经整理得出:f(x)>f(x*)+∇f(x*)T(x-x*)
充分性:设对任意的x*,x∈S,有f(x)>f(x*)+∇f(x*)T(x-x*),令y是x*与x连线上某一点,即对某一个λ∈(0,1),有y=λx+(1-λ)x*。由于S为凸集,则y∈S,根据假设,对于点x*,x,y∈S,下列两式成立:
f(x*)>f(y)+∇f(y)T(x*-y),f(x)>f(y)+∇f(y)T(x-y),合并化简得到:
(1-λ)f(x*)+λf(x)>f(y)+∇f(y)T[(1-λ)(x*-y)+λ(x-y)]
=f(y)+∇f(y)T[λx+(1-λ)x*-y]
=f(y)
即f(y)<λf(x)+(1-λ)f(x*)
上式即f(λx+(1-λ)x*)<λf(x)+(1-λ)f(x*)
由凸函数的定义知f(x)是严格凸函数
定理1.3.3 设n元实函数f在凸集D⊂Rn上二阶连续可微,则f在D上是凸函数的充要条件是∇2f(x)对一切x∈D为半正定。
定理1.3.4 设n元实函数f在凸集D⊂Rn上二阶连续可微,则f在D上是严格凸函数的充分条件是∇2f(x)对一切x∈D为正定。其中∇2f(x)为Hesse矩阵。
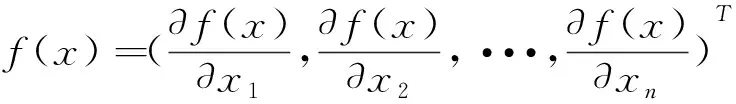
证明:
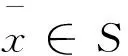
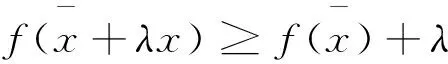
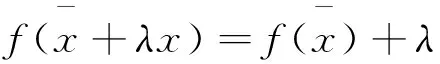
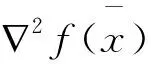
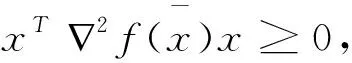

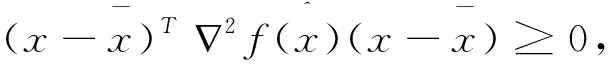
4 应用
4.1 判断下列函数的凸性:f(x)=x12+2x22
方法一:∀x,y∈D,D∈Rn,由公式得:f(x)≥f(y)+∇f(y)T(x1-y1,x2-y2)T,则
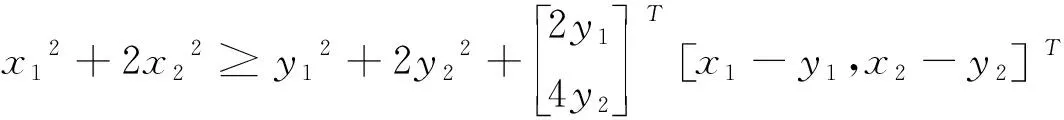
x12+2x22-y12-2y22-2x1y1+2y12-4x2y2+4y22≥0
(x1-y1)2+2(x2-y2)2≥0
因此得到f(x)为凸函数
方法二:∇f(x)=[2x1,4x2]T
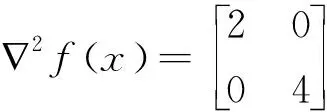
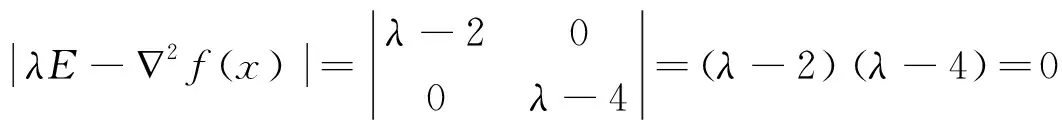
则λ1=2,λ2=4,可得∇2f(x)为正定矩阵,因此f(x)为凸函数。
4.2 判断下列函数的凸性:f(x)=x12+x22+…xn2
∀x,y∈D,D∈Rn,由公式得:f(x)≥f(y)+∇f(y)T(x1-y1,…,xn-yn)T
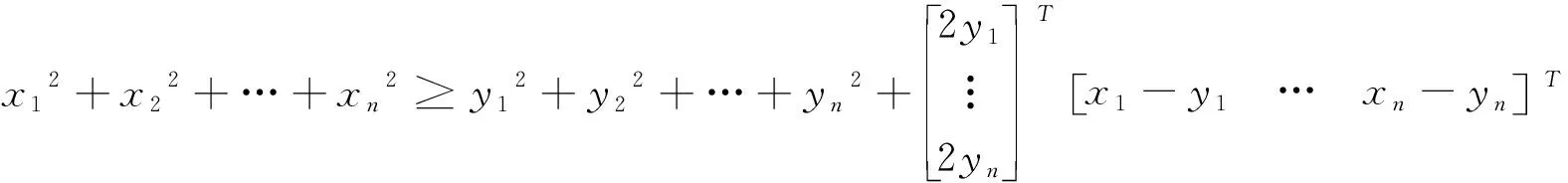
x12+x22+…xn2≥y12+y22+…+yn2+2x1y1-2y12+…+2xnyn-2yn2
(x1-y1)2+…+(xn-yn)2≥0
因此得到f(x)为凸函数。
4.3 判断下列函数的凸性:f(x)=x12+2x22+5x1x2
方法一:∀x,y∈D,D∈Rn,由公式得f(x)≥f(y)+∇f(y)T(x1-y1,x2-y2)T,则
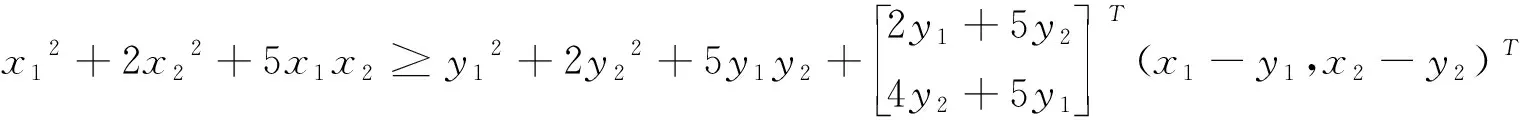
x12+2x22+5x1x2≥y12+2y22+5y1y2+(2y1+5y2)(x1-y1)+(4y2+5y1)(x2-y2)x12+2x22+y12+2y22+5x1x2-2x1y1-5x2y1-5x1y2-4x2y2+5y1y2≥0
当x1=0,y1=0,x2=1,y2=-2时,代入上述不等式左端,所的值小于0,不满足上述的不等式,因此得到f(x)为非凸函数。
方法二:∇f(x)=(2x1+5x2,4x2+5x1)
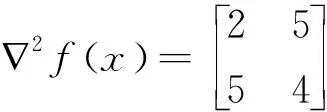
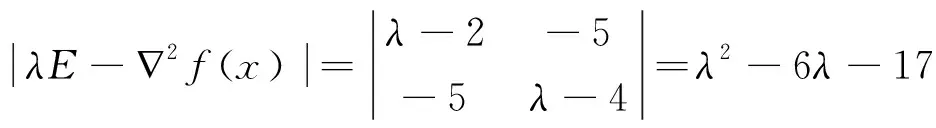
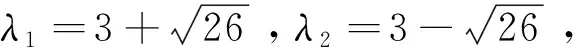
4.4 判断下列函数的凸性:
f(x)=x12+x22+…+xn2+x1x2+…+x1xn+x2x3+…+x2xn+…+xn-1xn
证明:∀x,y∈D,D∈Rn,由公式得f(x)≥f(y)+∇f(y)T(x1-y1,…,xn-yn)T,则
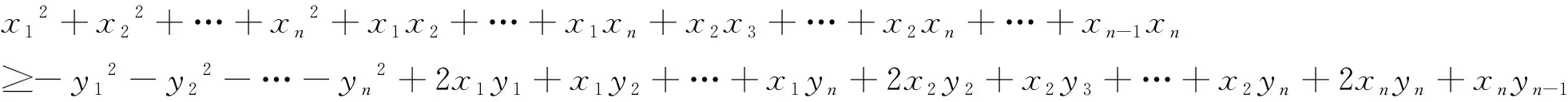
5 结论
若f(x)=ax12+bx22+…+mxn2,其中a,b,…,m∈R,n≥1,则f(x)为凸函数。
若f(x)=ax12+bx22+…+mxn2+lx1x2+…+px1xn+…+qxn-1xn
其中a,b,…,m,…,l,…,p,…,q∈R,n≥1,则f(x)为非凸函数。
