概率论在生活中的应用举例

常会敏

（国家开放大学 应用数学学院，北京 100039）

概率论的起源与赌博有关，著名的“分赌金”问题就是概率论的萌芽发展。由于概率论丰富的内容和研究对象的广泛性，使得它逐渐渗入很多相关领域。近年来，随着科学技术的迅猛发展，概率论已经在经济、教育、心理学等方面发挥着至关重要的作用，也在日常生活中影响着我们的决策。

一、赌博与概率论

【案例】2018年，金立手机品牌创始人刘立荣亲口承认在塞班岛参与赌博，从金立“借用”了资金，输了大概“十几个亿”，直接导致金立集团资金断裂。同年11月，金立申请破产重组。赌博可能不是导致金立破产的根本原因，可却毁掉了一个人的大好前途，让刘立荣人格破产。

概率论中有一个著名的赌徒输光定理：在“公平”的赌博中，任一个拥有有限赌本的赌徒，只要长期赌下去，必然有一天会输光，即“赌久必输”。下面从概率论的角度给出严密的解释。

假设赌徒的初始资金为n（任何一个赌徒，不论多么富有，n总是一个有限值），每赌一次或赢或输，资金分别变为n＋1或者n-1，输或者赢的概率都为0.5。设P(n)表示从n开始一直赌下去，资金变为0的概率，显然有P(0)=1，并且容易得到递推关系

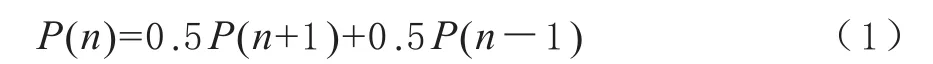
（1）式变形可得关系式

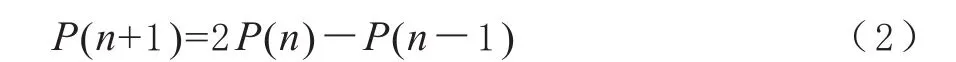
我们假设P(1)=a(0≤a≤ 1)，由（2）式知

P(2)=2a-1,P（3）=3a-2,…,P(n)=n(a-1)+1

由概率的性质可知P(n)=n(a -1)+1≥0对于任意大的n都成立，故a接近于1。对于任意数n，P(n)也接近于1。

因此，无论一个人多么富有，即使以0.5的胜率参与赌博，如果长期赌下去，必然有一天会输光。每个人都应该远离赌博，杜绝赌博恶习，洁身自好。

二、彩票与概率论

【案例】2010年开始，上海的徐某喜欢上了买彩票。刚开始，他购买彩票尚能量力而行，运气好还中过奖，这让他感觉买彩票既好玩又能赚钱，逐渐上瘾，每次出手经常是两三万元买彩票。徐某就这样沉迷于买彩票六七年，前后花费600多万元买彩票。可惜的是，他买得越多，“输”得越多，结果搞得倾家荡产、走投无路，在向彩票站老板借钱遭到拒绝后，竟当场泼洒酒精焚烧彩票机，触犯法律。结果徐某被浦东新区人民法院以放火罪一审判处有期徒刑四年。

我国的彩票分为体育彩票和福利彩票两种，是由国家统一发行的，目的是筹集社会公众资金，资助福利、体育等社会公众事业。[1]因而购买彩票应该本着娱乐的心态，为国家筹集资金，奉献爱心，而不应该沉迷于彩票，靠彩票发家致富。一张彩票的中奖概率有多大呢？下面以双色球为例，用概率论的知识计算彩票中奖的概率。

双色球为两区号码投注，投注号码由6个红色球号码和1个蓝色球号码组成，红色球号码从01—33中选择，蓝色球号码从01—16中选择。投注者所选单注投注号码与当期开出中奖号码相符的球色和个数确定中奖等级，假设中奖等级与相应的奖金按如下分布（见表1）。

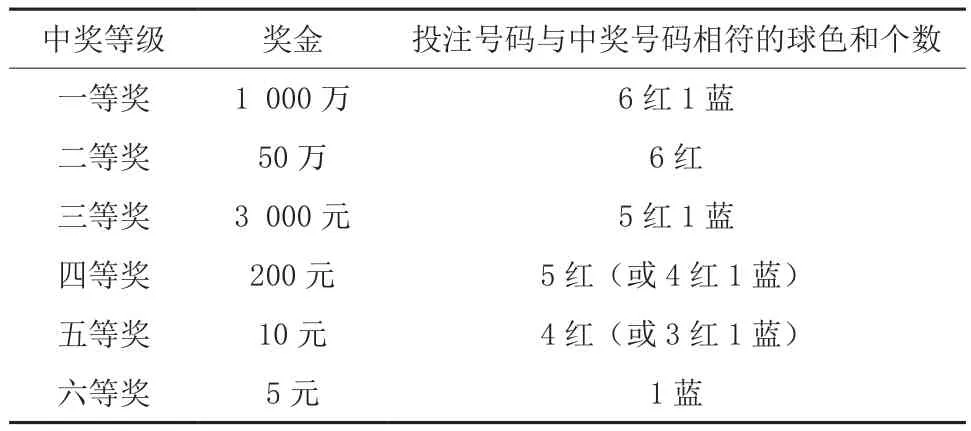
表1 双色球中奖等级与相应的奖金分布

设Pi表示中i等奖的概率（其中i=1,2,3,4,5,6），由概率论的知识得到

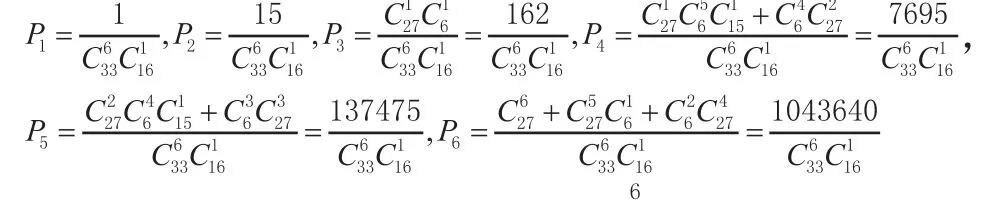
假设购买一张双色球需要花费2元，设X表示购买一张双色球所得利润，则X可能的取值为1 000万、50万、3 000、200、10、5、-2（为了计算的方便，中奖时所得利润没有减去花费2元），则随机变量X的分布列如下（见表2）。

表2 随机变量X的分布列

因而购买一张彩票所得利润的期望

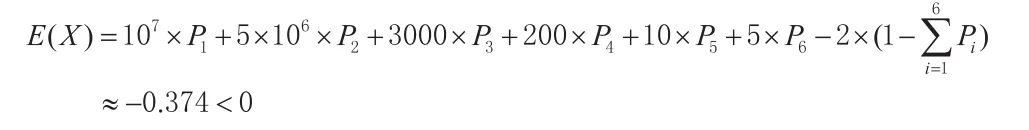
即每购买一张彩票，平均收益是负值。

因而购买彩票要有平和的心态，千万不能被一等奖的巨额奖金冲昏头脑，甚至不惜借钱购买大量彩票，最终只能导致与长期赌博有同样的下场。

三、保险与概率论

【案例】王先生是一位身材魁梧的东北汉子，靠自己的努力在北京扎根买房，还组建了一个幸福的家庭。为抵御小家可能遭遇的风险，2010年，王先生在某保险公司为自己投保了终身男性重大疾病险保额10万，同时购买了提前给付重大疾病保险，保额40万。2018年底，王先生感觉上腹胀痛，起初以为是慢性胃炎发作，并未重视，但症状逐渐加重，疼痛难忍，于是王先生去某医院检查，经医生详细检查后确诊为“原发性肝癌”。王先生得知病情后，及时联系保险公司的服务人员，申请理赔并递交相关材料，最终保险公司支付王先生保险费共计50万元。

保险，是现代出现频率比较高的一个词汇，与我们的生活息息相关，例如汽车保险。保险最大的意义是，用最小的成本进行风险转移，从而保障生活中小概率事件的产生，以降低损失等。如果是发生频率高且损失大的事件，一般情况下保费会很高，甚至保险公司会拒绝承保。我国的保险行业是一个盈利机构，且存在巨大的利润，2019年第一季度保险行业整体盈利763亿。究其原因，就是成功的运用了小概率事件原理。下面通过一个例子看保险公司如何盈利。[2]

某一保险公司，有2 500个同一年龄层的相同社会阶层的人参加保险，在一年内，每个人死亡的概率为0.002.每个参加保险的人在1月1日支付12元保险费，如果他在这一年内死亡，家属可以从公司领取保险费2 000元，求此保险公司亏本的概率。

分析：该保险公司一年内的收入为2 500×12=30 000元，假定投保的人一年内死亡x人，则公司应赔付的钱为 2 000x，因此当 2 000x＞30 000，即x＞15时，该公司会亏本。已知x～B(2 500,0.002)，求的是概率P(x＞5)。

由泊松定理：对于二项分布B(n,pn)，若当n→ +∞时，n pn→λ（固定常数），则，当n很大而p很小（通常要求p＜0.1），np大小适中（通常≤ 5）时，二项分布的概率函数近似等于泊松分布的概率函数。

解：假定参加保险的人一年内死亡x人，x＞15时，该公司会亏本。已知x～B(2 500,0.002)，由泊松定理，

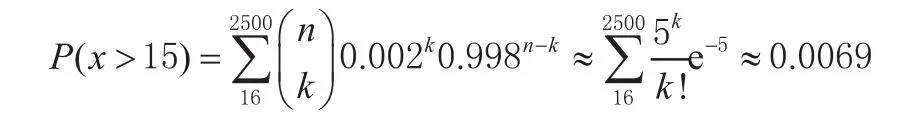
“保险公司赔钱”是一个小概率事件。事实上，该公司在本年获利小于10 000元的概率是0.014，即正常情况下，该公司获利不会少于10 000元。

四、相互宝与概率论

2018年10月16日，由蚂蚁保险和信美联合推出相互保险新产品——相互宝。截至2019年5月，已有超过6 000万人加入了相互宝计划。相互宝具有如下特点：门槛低，0元加入；可随时退出；覆盖全，可覆盖100种重症疾病；额度高。如果成员生病，最高可获得30万的互助金；分摊费用少。一人生病，大家分摊，2019年分摊费188元封顶。相互宝每月14日、28日为分摊日，根据加入的人数和患病的人数决定分摊金额的多少，下面通过一个例子感受相互宝的强大作用。

假设相互宝中成员人数为5 000万，公示100个出险案例，按最高赔付金额100×30万=3 000万元，加上协议中规定的10%管理费即300万元，那么在分摊日，就是5 000万人平摊3 300万元，人均分摊3 300÷5 000=0.66元。相互宝一年分摊费用预估在100—200元之间。

对于一个健康的人来说，虽然得100种重症疾病中的某种疾病是一个小概率事件，但也有可能不幸发生。相互宝每月的分摊费用很低，正是这种“抱团取暖”的思路，低分摊、（相对）高赔付，因而不断有成员自愿加入相互宝。

五、结束语

概率论知识起源于生活，反过来又指导和影响着我们的生活。充分利用概率论知识与生活的紧密联系，结合生活中的有关案例，有助于我们的日常教学。将有趣且与知识点相关的例子应用于课堂教学，能激发学生的学习兴趣，[3]培养学生善于思考、分析问题和解决问题的能力，也有助于学生数学建模能力的构建，以期为社会培养更多应用型的数学人才。