基于实船数据的船舶航速与油耗优化建模

2020-04-16刘敬贤

中国航海 2020年1期

袁智，刘敬贤，刘奕，杨鑫

(武汉理工大学 a.航运学院；b.内河航运技术湖北省重点实验室，武汉 430063)

随着全球贸易的不断增长，世界各地的水上交通也越来越繁忙。船舶作为水上交通最主要的运输工具，不合理的能源消耗不仅增加运输成本，还会排放大量的污染气体。有研究报告[1]显示:目前全球航运业每年排放的CO2超过12亿t，约占全球碳排放总量的4%。早在2010年，国际海事组织(International Maritime Organization,IMO)[2]就强制实施船舶能效管理计划(Ship Energy Efficiency Management Plan,SEEMP)。2015年开始，IMO针对所有新造船舶另行引入船舶能效设计指数(Energy Efficiency Design Index,EEDI)[3-4]作为评价标准，用以在设计和建造阶段量化评估新建船舶的能耗水平。船舶处于最佳航速是实现燃油最大效率、降低运输成本、减少气体排放的有效方法。魏应三等[5]将船舶航速的优化抽象为对目标函数求极值的数学问题，研究恒速航行对船舶总耗功的影响。李铮等[6]基于遗传算法对不定期船舶运输的航速优化问题进行研究。FAGERHOLT等[7]根据船舶的历史油耗数据，利用线性插值拟合油耗与航速的关系。WONG等[8]用三次函数拟合船舶油耗与航速的关系，并利用对数效用和线性效用模型得到权衡油耗、碳排放和到货时间的最佳航速。马冉祺等[9]通过离散化思想，建立以航速为自变量、燃油消耗量为应变量的航速优化模型，并采用遗传算法进行优化计算。楼狄明等[10]通过拟合油耗、排放与航速的关系、建立巡航工况下的航速优化模型，对拖船的最佳油耗和排放对应的航速进行分析。LINDSTAD等[11]基于船舶参数、天气条件、海洋条件、运营成本等与航速相关的变量建立远洋散货船盈利、成本和排放的预测模型。以上研究采用的都是基于单方面的理论公式、数学统计方法或者实测数据，并没有将理论公式、计算方法和实测数据结合起来。因此，本文基于实测数据，在充分分析船舶油耗模型影响因素的基础上，采用物理方程、数学公式和神经网络构建船舶航速与油耗优化模型。

1 船舶油耗影响因素分析

从物理的角度看，船舶航行过程中主要受推力和阻力的作用，推力主要是发动机带动螺旋桨产生的，阻力则包括水、风、流等产生的阻力。因此，在船舶油耗模型中，可将影响因素分为船舶推进系统[13]的功率转换和船舶航行过程阻力变化两大环节。

1.1 船舶推进系统功率转换分析

船舶在航行过程中，发动机消耗燃油产生最初的功率Pe，发动机带动螺旋桨转动产出螺旋桨功率Pp，螺旋桨在水下转动给船体一个有效的推进功率Ps，最终使得船舶获得一个使其前进的推力。在这个过程中，推进功率进行两次传递和转化，考虑每次的转换效率，假设η1为发动机功率转换效率，η2为螺旋桨功率转换效率，则船舶推进系统的功率转换关系见图1。因此，发动机的转速、螺旋桨距是影响船舶推进功率的因素。

图1 船舶推进系统的功率转换关系图

1.2 船舶航行过程阻力变化分析

船舶受到的航行阻力主要分为水流阻力和空气阻力。水流阻力又可细分为静水阻力和浪增阻力。其中:静水阻力为船体平板与水接触产生的摩擦阻力和船体表面的兴波阻力；浪增阻力与入射波高的平方关系成正比[14]；空气阻力主要是船体水位线以上部分受到空气影响而产生的阻力。除此之外，船舶的艏艉吃水比以及偏航对船舶的阻力也产生一定的影响，所以船舶排水量、艏吃水、艉吃水、船长、型深、型宽、方形系数也是影响船舶阻力的因素。综上，船舶油耗影响因素见图2。

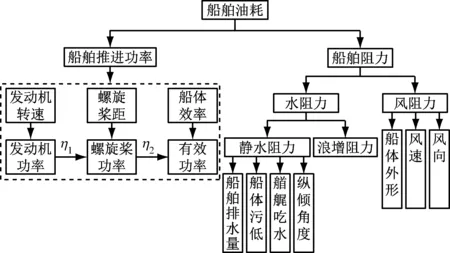
图2 船舶油耗影响因素

2 基于灰箱模型理论的船舶航速与油耗模型

灰箱模型(Grey-Box Model,GBM)理论[15]是在研究系统控制不确定因素时被提出的，即系统中部分信息已知，而有部分信息未知或者不确定。与之相对应的还有白箱模型(White-Box Model, WBM)和黑箱模型(Black-Box Model,BBM)。WBM通过物理原理和相关回归计算公式以及实船试验结果可分析和计算船舶航行过程中的阻力性能。例如:在无风情况下，可通过半经验公式计算出船舶的静水阻力；在缺乏风阻系数的情况下，基于模型试验结果推导出船舶风阻的半经验公式也具有一定的参考价值。与WBM不同的是，BBM不需要知道关于系统模型的任何先验知识和思考，输入与输出的关系仅仅通过试验数据来模拟，多采用人工神经网络方法[16]，可用来对白箱计算的结果进行校准。因此，可将GBM看作是BBM和BBM的结合体。

利用GBM研究船舶航速与油耗的时候，已知的部分可通过明确的物理方程以及数学函数建立确定的WBM;而未知的部分可通过BP (Back Propagation)神经网络构成的BBM来模拟。因此，建立基于GBM的船舶油耗模型见图3。

由图3可知:基于GBM的船舶航速与油耗模型中，WBM用来建立推进动力和船舶阻力之间的物理平衡方程，BBM根据给定的航段信息来调整WBM的输出。

在GBM中，有串行和并行两种结合方式。典型的串行方式是GBM在WBM之前，对原始数据进行预处理再输给WBM，这时BBM看作是一个回归模型，见图4a。并行的GBM中，见图4b。其建模方法为：

1) 构建一个WBM。

2) 通过最小化WBM输出和期望输出之间的误差来“训练”BBM。

3) 组合WBM和BBM。

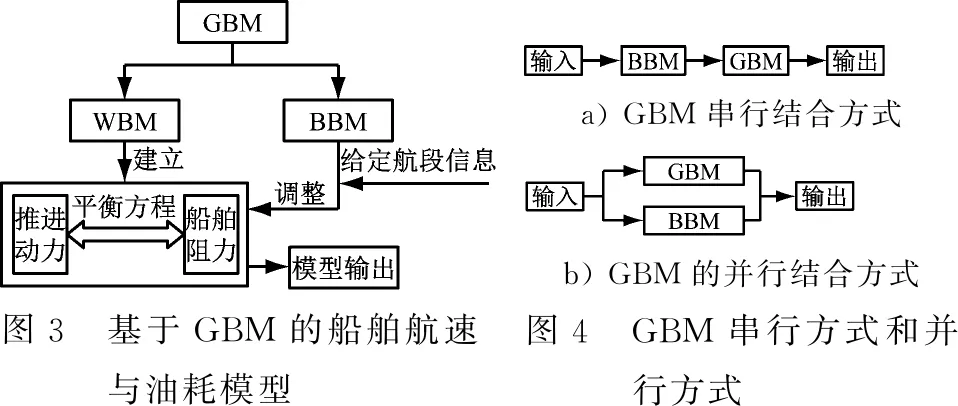
图3 基于GBM的船舶航速与油耗模型a) GBM串行结合方式b) GBM的并行结合方式图4 GBM串行方式和并行方式

3 船舶航速与油耗优化模型构建

根据对船舶油耗影响因素的分析结果和GBM理论，本文的船舶航速与油耗优化模型包括WBM和BBM，具体构建如下。

3.1 模型参数定义

考虑船舶油耗各种影响因素，定义航速与油耗优化模型的参数见表1。

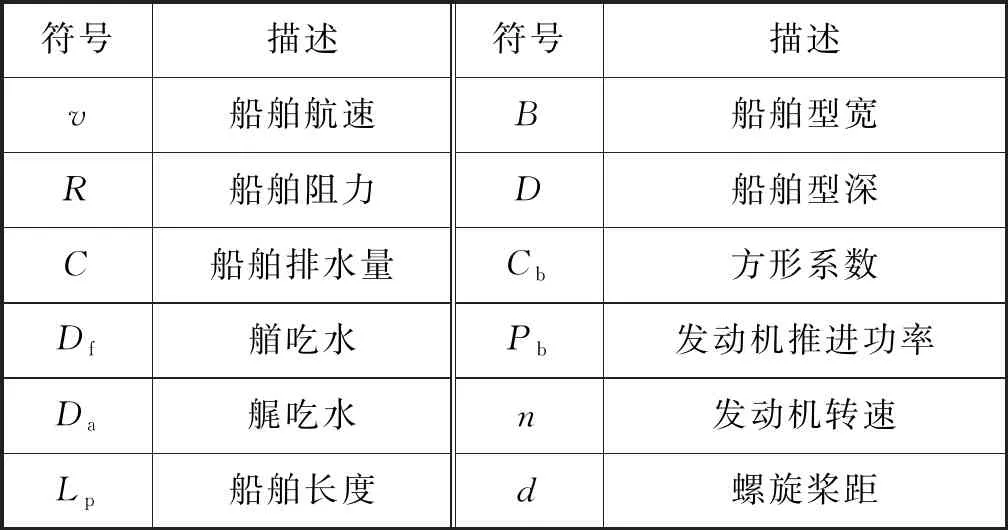
表1 模型参数

3.2 模型构建

根据物理学中的发动机功率与速度的关系，有

P=F·v

(1)

式(1)中：P为发动机的功率;F为发动机的牵引力;v为速度。船舶在以一定的速度航行过程中，受到的阻力与牵引力相等。因此，有

Pb=Rt·v

(2)

式(2)中：Rt为船舶受到的总阻力。根据前面的分析，Rt计算见式(3)。

Rt=RF+Rw+RA

(3)

式(3)中：RF为船舶摩擦阻力;Rw为浪增阻力;RA为船身阻力。这些阻力可参考J.Holtrop系列公式[17]进行计算求解。

综上，构建BBM如下:

v·R(v,C,Df,Da,Lp,B,D,Cb)=Pb(n,d,v)

(4)

方程(4)考虑各影响因素，用函数的形式表示船舶阻力R(v,C,Df,Da,Lp,B,D,Cb)和船舶推进功率Pb(n,d,v)。不难发现船舶阻力和推进功率都与船舶航速有关,而C、Df、Da、Lp、B、D、Cb、n、d这些属于船舶设计参数，其参数值可直接从船舶制造厂商查询。因此，在求解式(4)的时候，固定其他参数，以航速为变量定义方程为

F(v)=v·R(v)-Pb(v)

(5)

对于方程(5)采用牛顿-拉普森迭代算法[18]求解，设置迭代算子为

(6)

式(6)中：vi和Vi+1分别为第i和i+1次迭代的航速值。由式(6)可知：知道了航速v的值，就可以计算得到推进功率Pb(v)，再根据发动机的转速就可以计算出船舶耗油量F。

通过BBM模型计算可得到的航速与油耗的关系。但是，还有一些影响船舶阻力的气象、水文等因素不好模拟成输入量，因此计算的结果还存在比较大的误差。可利用BP神经网络构建BBM模型，把WBM输出的结果作为网络的输入，并考虑选定航段的航行环境，通过网络训练输出更加精确的航速与油耗关系。即基于GBM模型构建这样的船舶油耗模型：利用物理方程和经验公式构建WBM模型，将初步计算的结果输出给人工神经网络构建的BBM模型，再经过训练最终得出更准确的船舶航速与油耗量关系。

综上，将v、C、Df、Da、Lp、B、D、Cb、n、d这些船舶油耗量影响因素作为输入参数，F作为输出参数，结合WBM和BBM构建船舶油耗模型见图5。

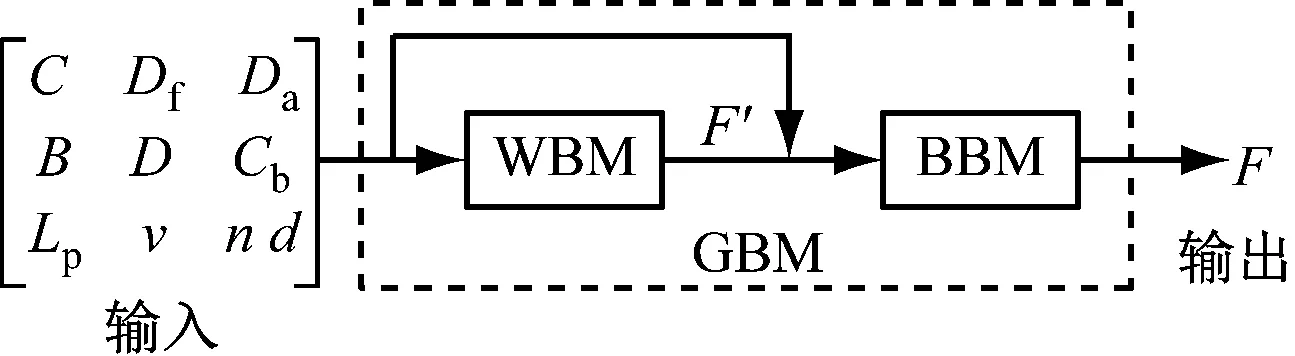
图5 基于串行GBM的船舶油耗模型

同时，根据灰箱理论，我们还以并行结合的方式构建船舶油耗模型，见图6。与串行的方式相比，并行方式中多了BBM的输出F″，F′表示人工神经网络训练的结果，再与WBM计算的结果相加得到最终的F。

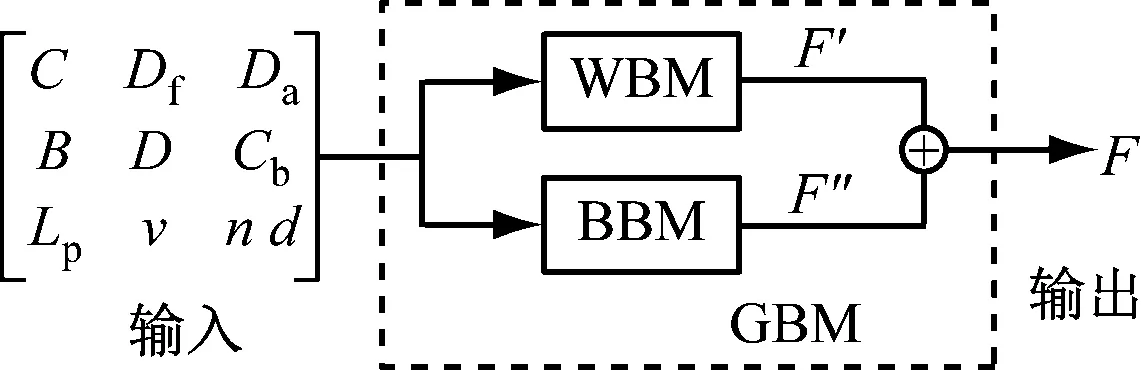
图6 基于并行GBM的船舶油耗模型

4 船舶航速与油耗优化模型验证

4.1 实测数据预处理

研究的实测数据来源于长航货运公司提供的特定航次的油耗报表记录。选取载货量为5 094 t新长江船型的散货船在长涪航段2018年4月30 d的数据，包括每天的航行路线的起始位置、航行里程、航行时间、航行速度、油箱储油记录，剔除中间停港卸货、装货、休整期的数据得到可用的93条记录。取该航段的平均航速和油耗数据见图7和图8。

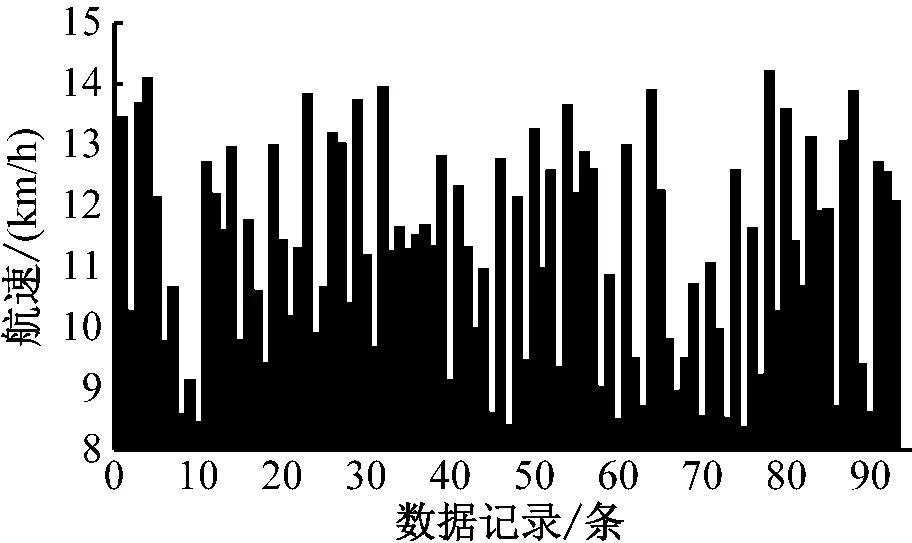
图7 船舶平均航速实测数据

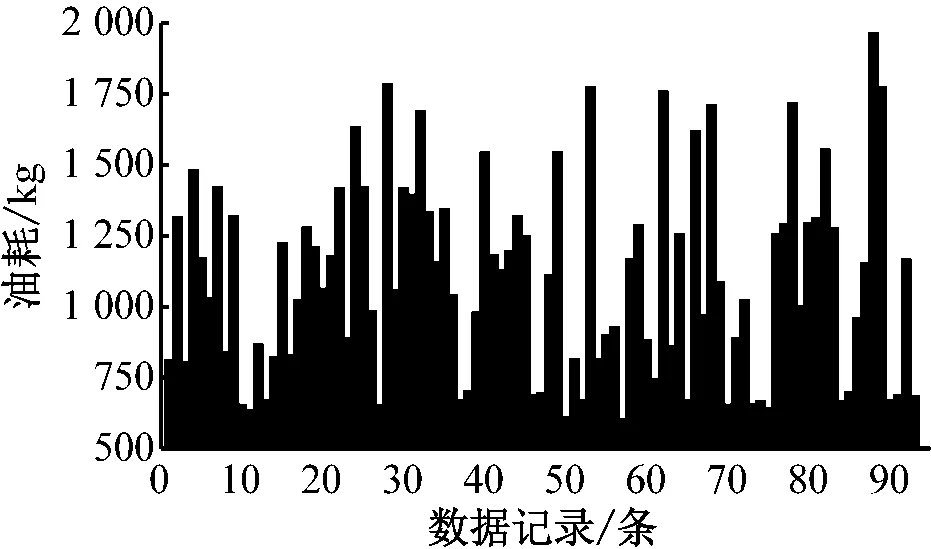
图8 船舶油耗实测数据

由图7可知:船舶平均航速在[8.2,14.4] km/h(1 kn=1.852 km/h)，油耗在[600,1 900] kg。同时，影响船舶油耗的其他船舶设计参数都已通过调研从公司和船舶厂商那里获得。

4.2 优化模型验证结果分析

根据构建的船舶油耗模型，将从公司和船商获得的设计参数和实测数据作输入船舶油耗模型中进行验证。油耗模型中的BBM采用多层感知机的BP神经网络：包含输入层、隐含层、输出层，输入层和输出层的节点数为5个和3个，隐含层节点数通常采用经验公式见式(7)，以此值作为初始值，并通过多次试验进行试凑，最终选取多次训练之后识别误差最小的值作为隐藏层节点数为6。

M=n+m+a

(7)

式(7)中：M为隐藏层节点数；m为输入层节点数；n为输出层节点数；a为[0,10]内的常数。

基于实测的船舶航速和油耗数据，分别采用单一WBG和GBM进行试验，并将模型输出的结果进行多项式拟合，得到WBG、GBM输出的拟合曲线分别见图9和图10。进一步得到图9和图10中拟合曲线的R2和RMSE见表2。

由表2可知:GBM模型的R2达到了0.945，而且GBM模型输出的RMSE只有0.071，依次比WBM的输出和原始数据减少了接近1/2，表明基于GBM的船舶油耗模型输出的结果能够更好地描述船舶航速和油耗的关系，见图11。

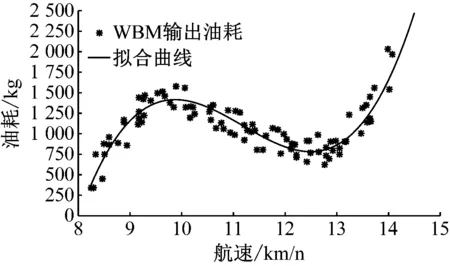
图9 单一WBM模型输出油耗与航速曲线

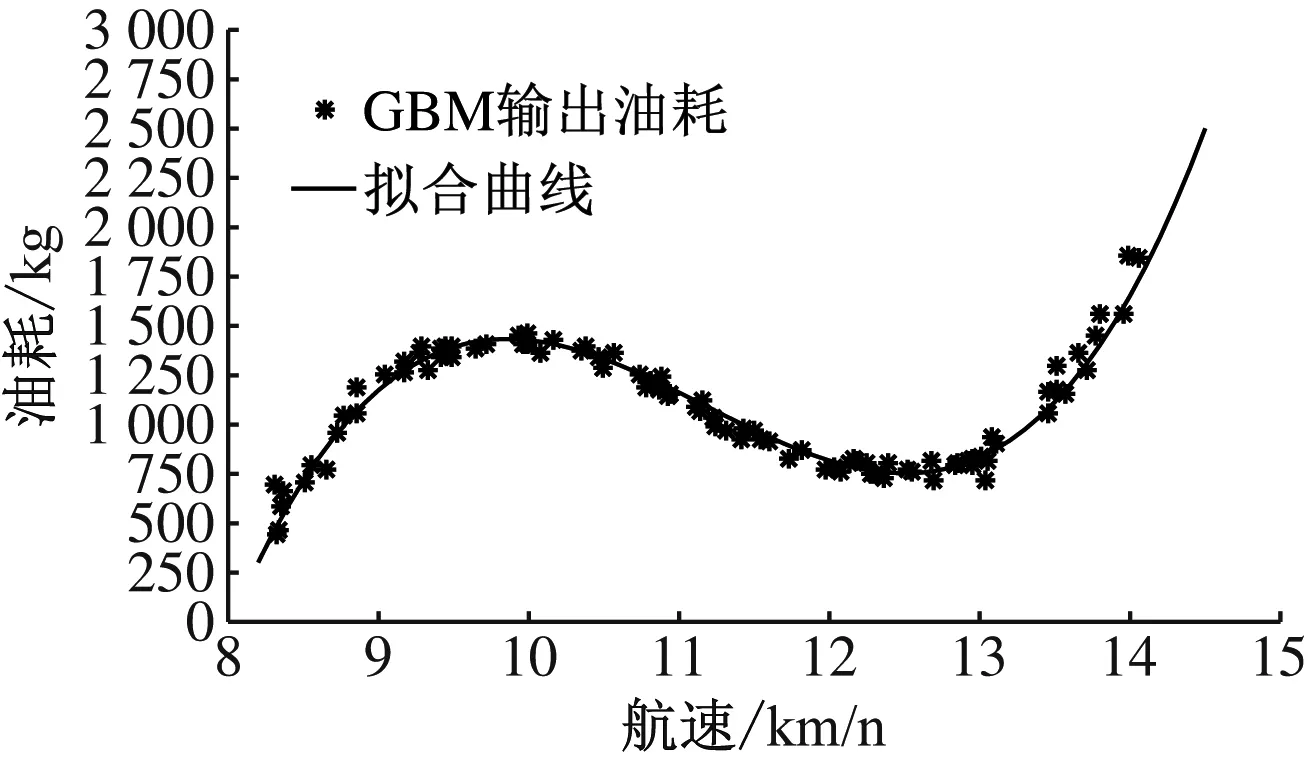
图10 GBM模型输出油耗与航速曲线

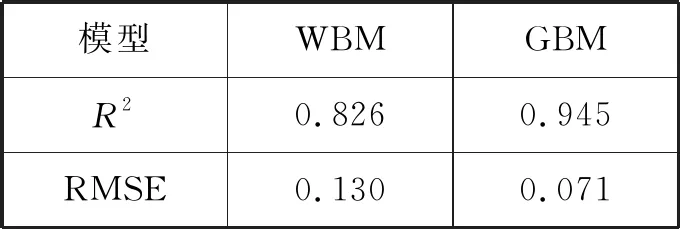
表2 船舶油耗与航速拟合参数

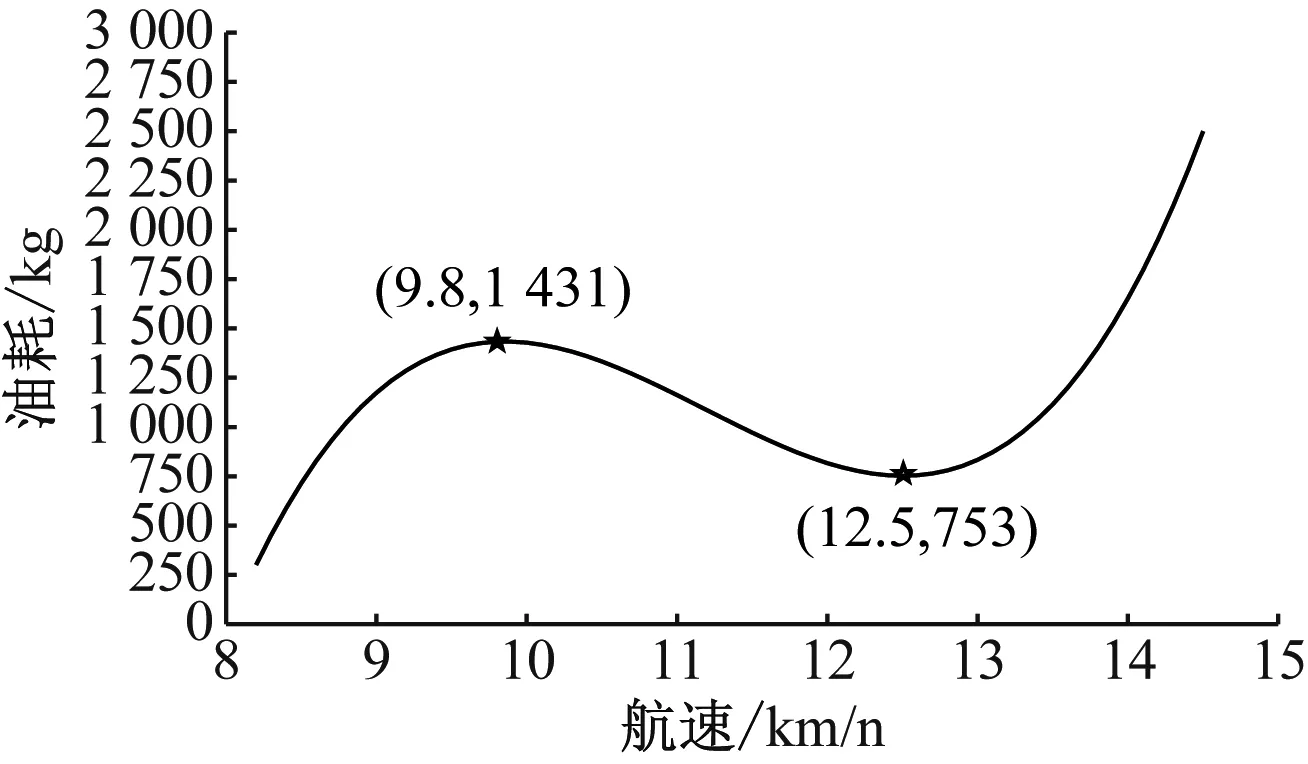
图11 船舶油耗与航速关系

由图11可知：航速在9.8 km/h之前，随着航速的增加油耗也随之增加；在高于9.8 km/h之后随着航速的增加油耗随之减少，且变化的速度有所减慢；而当航速达到12.5 km/h之后，油耗迅速随之上升。这些变化规律在实际航行过程中可很好地指导船舶操纵，通过调整航速控制燃油消耗，实现燃油效率的最大化。