基于高频中值滤波的小波滤波在脑动脉色素浓度谱特征信号提取中的应用*

朱翔宇，姜馨儿，田兆红，修采，查雨彤

(上海健康医学院 上海穿戴式医疗技术与器械工程研究中心，上海 201318)

1 引 言

近年来，由于人们生活环境、生活习惯等因素影响，脑梗塞、脑出血、脑卒中等脑血管疾病和并发症的患者明显增多。在脑血管疾病诊断中，多采用脑血流动力学参数作为重要的诊断指标。目前，疾病的常规临床检查技术无论是生化检测还是影像学检测，均需要固定在指定区域，且存在使用成本高，易产生副作用等问题。因此给实时监测脑血流动力学参数增加了难度，耽误治疗。与此同时，诊断的准确性高度依赖于医生的诊疗技术，增加误诊和漏诊的风险。

近红外光谱技术(NIRS)与目前常规的临床检测技术相比，具有瞬时分辨率高、放射性低、无创等优点[1]。20世纪80年代末，Ferrari和Edwards基于菲克原理，提出了利用NIRS测量脑组织能量代谢和血液循环。这种方法在当时引起了广大学者的关注。氧合血红蛋白(oxyhe myoglobin, HbO2)作为脑血流动力学的示踪剂，首次用于脑血流动力学的定量分析，但对于脑损伤或其他易受氧饱和度降低影响的疾病患者，脑血流动力学参数不能对吸收的HbO2的变化做出精确的反馈。

为了解决这些问题，本课题组已经设计了反射式光电传感测量装置，并通过提前注射指示剂染料吲哚菁绿(indocyanine green, ICG)能够进行同步和实时测量[2]。虽然该方法对脑血流动力学参数的采集十分有效，然而还是包含着组织光吸收干扰、心动、呼吸带来的干扰，以及一些测量过程中的无关噪声。因此，这就需要采取有效的滤波手段提取特征信号[3-4]。目前常见的滤波方法普遍存在滤波后信号易失真，不能有效滤除低频或者高频噪声的问题[5]。为达到理想的滤波效果，本研究采用中值滤波和小波滤波，通过结合这两种方法，以实现在同时滤除不同频率噪声的基础上不失真，改善了现有的问题。

2 原理

2.1 脑血流动力学参数的测量

血流动力学参数的测量包括脑血流量(CBF),脑血容积(CBV) 和平均通过时间(MTT)等血流参数。CBF, CBV 和 MTT都是基于菲克原理计算的血流参数。这些参数体现了示踪剂在器官组织中的积累量以及示踪剂在器官中的到达率与解离率之间的差异[6]。

(1)

其中，Q、CA和CV代表组织、动脉和静脉中的示踪剂浓度，F为血流。当t小于通过器官的最小通过时间时，示踪剂将不会出现在静脉血液中，故在0到t的时间间隔期内静脉血液中无示踪剂流出，上式被简化为式(2)以计算血流量。

(2)

对于注射的示踪剂，积累量是随着脑组织中ICG的总浓度ΔC[ICG]tissue增加而变化的，脑内ICG动脉引入量表示为ΔC[ICG]blood。根据菲克定律，CBF以式(3)表达，其中kICG是ICG的分子量。

(3)

CBV是血液与脑组织体积的比值，其计算为测量期间脑组织和动脉血液中ICG浓度积分的比率。

(4)

根据中心体积原理，平均通过时间(MTT)可以计算如下：

(5)

从上述公式可以看出，脑组织和脑动脉的ICG浓度是脑血流动力学检测的最关键指标。因此，使用何种方法进行测量，在一定程度上决定了整个脑血流动力学参数的准确性。通过NIRS技术，建立脑血流动力学模型，利用光电手段，获得光电容积脉搏波(PPG)信号，从中可以获得吸光物质的浓度变化情况，进而获得示踪剂ICG的浓度。

2.2 NIRS-ICG技术脑血流动力学模型的建立

脑血管侧支循环丰富，呈网络状分布，通过检测动脉的搏动情况能够获得大量有价值的信息。脉搏是当大量血液进入动脉后使管径扩张的节律性搏动，其光程的变化使血流中光的吸收强度随之改变。临床上常利用光电手段获取PPG用于实时监测，测量原理见图1。

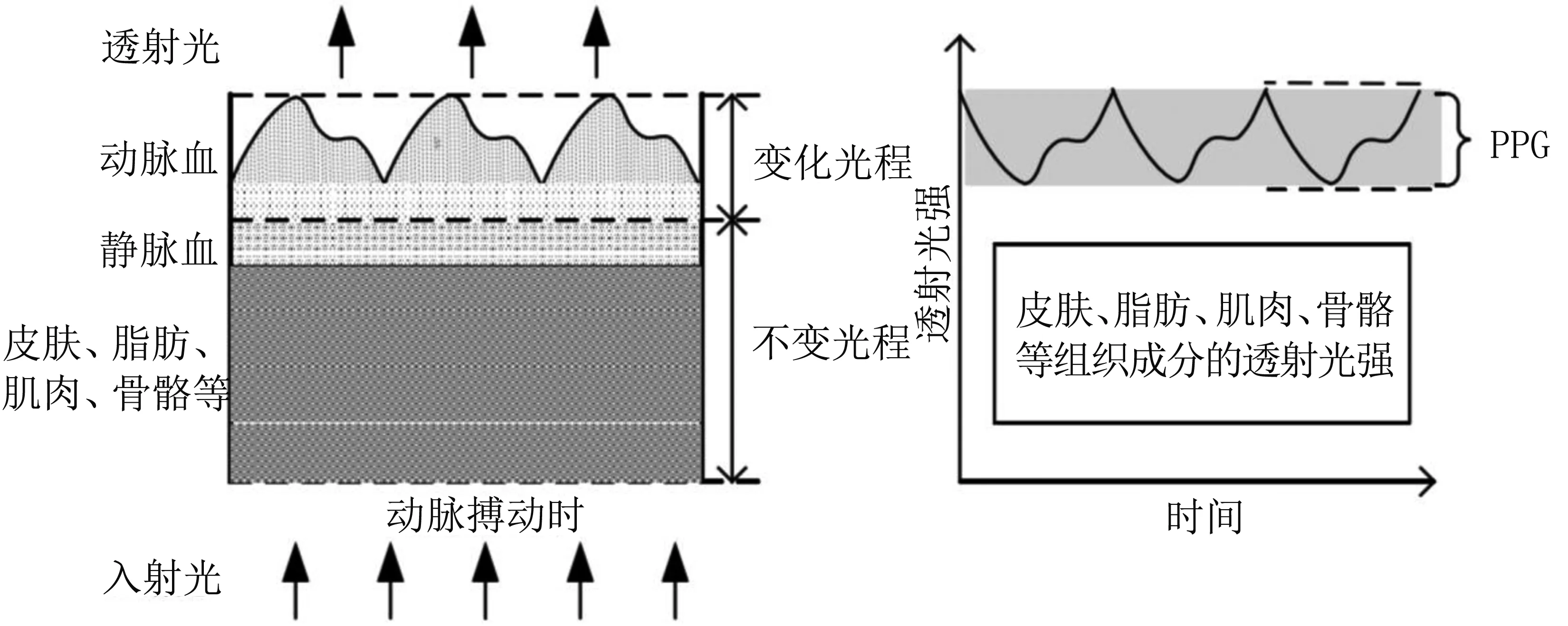
图1PPG的产生原理图

Fig.1The generate schematic of PPG

由于头部组织是一种高散射低吸收的不均匀介质，故在进行PPG信号测量时，整个被测区域可以视为既有光散射又有光吸收能力的对象。因此，吸光物质浓度改变所造成的光强变化遵从朗伯-比尔定律[7]。为了修正脑血流动力学状态异常条件下CHbT和cSaO2产生的波动，采用776、805和850 nm多波长近红外光源在测量过程中的时刻，与初始静息态的ICG浓度进行差分处理，得到修正后的ICG浓度。

(6)

其中，Ф为光子通量率，T805、T850分别为：

(7)

(8)

3 实验方法

3.1 小波变换在脑动脉色素浓度谱特征信号滤波中的应用

3.1.1小波去噪 对信号进行小波去噪[8]，首先需将原信号进行小波变换。小波变换适合处理短时间内发生突变的信号，能够充分体现信号的每一个细节，对于PPG这类信号强度弱，易产生干扰的信号非常适用。利用塔式算法[9]进行小波变换，将一长度为 M 的信号分解为相等长度的小波系数[10]，并进行后续的滤波处理。根据其理论，对脑动脉色素浓度谱特征信号进行小波去噪的步骤以及注意事项如下：

(1)对特征信号做初步分析，采用小波变换[11]对含噪信号进行分解。根据分解层数越高，有效信号提取效果越好，均方误差越小的原则，选择合适的分解层数，但考虑到分解层数过高(大于6)，极易使部分PPG信号失真，致使重构后特征信号与原始信号差异过大，影响后续的参数分析，所以这里分解层数应等于6；

(2)对于步骤(1)中分解所得到的分解系数，选择分层阈值函数，进行阈值化处理，对各尺度小波系数去噪。通过分层阈值函数后的小波系数能够在保留信号主要特征的情况下,整体连续性更佳，便于进行PPG信号重构；

(3)对小波进行逆变换，将经分层阈值函数处理过的小波系数加以重构，由此得到小波滤波去噪后的特征信号。

3.1.2小波滤波中阈值函数的选择 在阈值函数的选择中，有两个较为常用的阈值函数，软阈值和硬阈值，但均不能满足该信号去噪的要求，对于该含噪信号，在进行去噪处理后，既要使去噪后信号的信噪比较高，还要考虑所得信号的平滑性。因此，在此引入了分层阈值函数，该函数结合了软阈值和硬阈值函数去噪的优点，在保留了尽可能多的信号特征的情况下，使重构后的信号过渡更加平滑，其表达式为：

(9)

式中，σ为噪声标准方差，j为小波分解层数，Tj为阈值。这里的N根据上文有关分解层数值的分析，取6为宜。这种方式减少了阈值处理的固定偏差，更好地保留了脉搏波信号在分解各层的特征，有效提升了降噪效果。

3.2 中值滤波

中值滤波是一种基于排序统计理论的能有效抑制噪声，并对脉冲信号有良好滤除作用的非线性信号处理技术。这种滤波方式的基本原理是将数字图像或数字序列中一点的值，用该点的一个邻域中各点值的中值来代替[12]，使周围的像素值接近真实值，由此达到消除孤立噪声点的效果。

中值滤波的数学表示为：

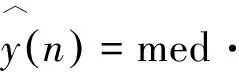
(10)

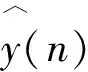
3.3 结合中值滤波和小波滤波的高频中值小波滤波

小波滤波在滤波处理上有独特优势，能对成分进行独立分析，但不能对粗差的剔除做到完善。中值滤波在有效解决粗差的剔除上，具有独特优势[13]。因此，本研究采用了基于高频中值滤波的小波滤波，用于处理采集的PPG信号，改善了仅采用小波滤波的局限性。

首先在改进算法中，对PPG信号用中值滤波处理，得到平滑且已经剔除高频噪声的信号。然后将处理后的信号进行小波分解，得到相对应的分解系数，再通过恰当的阈值函数[14]进行处理。最后将得到的系数重构，得到所需信号。

根据上述理论，可将基于高频中值滤波的小波滤波流程进行归纳，见图2。

图2高频中值滤波的小波滤波步骤

Fig.2The steps of wavelet filtering of high frequency median filter

具体步骤：

(1)对含有噪声的信号作初步分析，由于信号中的噪声主要以高频系数形式出现，所以，使用中值滤波处理信号中的高频系数部分；

(2)将得到的高频系数与信号中的低频系数加以重构，得到一个完成初步滤波的信号；

(3)在步骤(2)得到的信号上再使用小波滤波进行处理；

(4)选取合适的小波基，确定小波分解系数；

(5)对于步骤(4)中分解所得的分解系数，选择合适的软阈值或硬阈值进行阈值化处理，对各尺度小波系数去噪[15]；

(6)对小波进行逆变换，将经软硬阈值处理过的小波系数加以重构，最终得到基于中值滤波的小波滤波的特征信号。

4 实验过程

4.1 实验的评价手段

为了验证所提出方法的有效性，本研究利用表征观察值与真值离散均方根误差。其中，RMSE越小，信号处理结果越接近目标信号。

(11)

式中，N是样本xn的个数。

同时利用所得的均方根误差，计算信噪比，信噪比越大，说明混在信号里的噪声越小。信噪比单位为分贝(dB)。

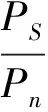
(12)

式中，Ps和Pn分别代表信号和噪声的有效功率。

信号的频谱图表明了信号在不同频率分量成分的大小，相比时域图像提供了更丰富具体的频域图像。可以利用离散傅立叶变换实现时快速算法[16]即快速傅里叶变换(fast fourier transform, FFT)，对所得信号进行频谱分析，在要求精度不高的情况下，可在频谱图中读出信号的成分，观察频谱图可以看出高频信号是否在经过中值滤波后被有效剔除。

(13)

式中，F(ω)为f(t)的像函数，f(t)为F(ω)的像原函数。

4.2 仿真实验

为了更好地比较不同滤波方式所达到的滤波效果，在使用从人体获取的真实脉搏波进行数据处理之前，利用功能强大的MATLAB，使用仿真技术构建调试环境，对真实信号进行仿真[17-18]。通过仿真技术模拟实验所获得的参数结果，为真实数据的处理提供必要参考。

4.2.1信号仿真的步骤 本研究按照PPG信号的大致趋势以及真实信号噪声成分复杂的特征进行构建，使构建完毕的仿真信号与真实信号相比能够获得理想的均方根误差值以及相关系数。

为了还原采样时实测光电容积脉搏波信号在一个周期内的变化，在构建时，选择了将正弦信号与余弦信号相叠加[19]，以还原真实信号走势，见图3(a)。

由于PPG信号是心脏跳动所引发的波动信号，因此，该信号的主要频率首先应根据心脏搏动所产生的心率来决定。临床上，我们往往用脉率(pulse rate，PR)来替代，根据成人在静息状态PR参考值为60次/min，构建脉搏容积波频率为1 Hz的仿真信号，见图3(b)。

由于实测信号在测量中受到多种干扰因素影响，尤其是呼吸产生的干扰[20]，进而使用高斯噪声来还原这种干扰。高斯噪声是一种较为泛用的噪声模型，根据成人的呼吸频率以及呼吸噪声[21]的不规则性分布，在信号不同的区间上，分别叠加了均值为0，标准差分别为30、20、5、15、19、2的正态分布高斯噪声，见图3(c)。

叠加后，图像呈现了较为明显的不规则性。此外在测量过程中还存在工频干扰以及测量设备传输过程中所产生的干扰，根据其特征，叠加了伽马噪声，该伽马噪声由三个服从指数分布的噪声叠加而成，对此仿真图像的构建具有十分显著的效果,见图3(d)。

仿真完成后，对构建完毕的仿真信号进行评价，将仿真信号与通过实测获得的真实信号进行对比，经计算，得到RMSE为2.38，相关系数为0.928，符合实验要求。

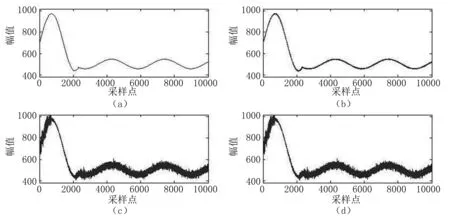
图3PPG仿真信号叠加

Fig.3Superposition of simulation PPG signals

4.2.2特征信号的提取 在MATLAB中导入了构建的仿真信号。为将其干扰噪声有效剔除，选择了常见且实用的中值滤波。将仿真信号放入中值滤波器。中值滤波后的图像见图4。

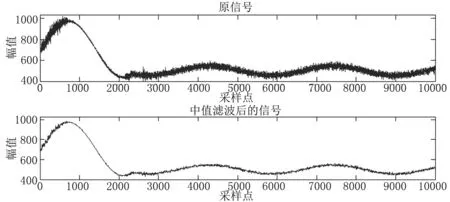
图4中值滤波效果图

Fig.4Median filter rendering

从图中可以看出，中值滤波对高频噪声有着较为显著的滤波效果。对比原信号和滤波后的频谱图，在高频区域内的噪声已经被完全剔除，符合实验目的。但是根据中值滤波后呈现出的频谱图像，见图5，能够发现低频信号并未被有效过滤，如呼吸、心动等频率低的干扰信号仍对特征信号的提取有一定影响。因此在中值滤波后再次选用了小波滤波。

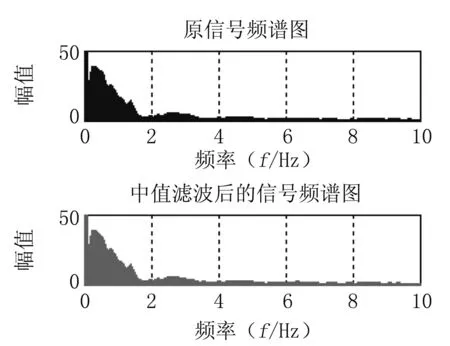
图5 原信号与中值滤波后的信号频谱图

利用小波滤波进行实验时，首先需要选用合适的小波基和分解系数(N=6)，之后对中值滤波后的信号进行分解，可以得到6层分解信号和位于第一层的中值滤波后信号，分解信号的图像按照频率由低到高依次排列。在阈值作用方式上，采用了能使图像更平滑的软阈值函数这一作用方式，同时也避免了硬阈值“一刀切”带来的影响。在阈值的选取方面，使用了分层阈值函数进行阈值选取操作，能使滤波后信号的相似程度更高。根据式(11)计算可得，每一层阈值分别为99.6031、74.6282、62.7461、55.4213、50.3208、46.5034。这样能使所得信号在相似度较高的基础上，确保光滑度。

通过观察中值滤波和组合滤波后信号的频谱分析图，可以看出，之前未被有效剔除的低频干扰信号，在结合小波滤波后被有效去除，效果见图6。综上，此组合方法能有效滤除仿真光电容积脉搏波的干扰噪声，可尝试将其运用于真实的光电容积脉搏波信号滤波。

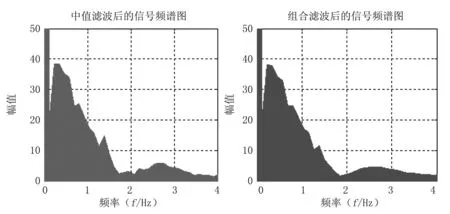
图6中值滤波后与组合滤波后的信号频谱图对比(低频部分)

Fig.6Comparison of signal spectrum after median filtering and combined filtering (low frequency part)

4.3 实测信号实验

按照仿真实验所采取的过程和方法，本研究利用仿真信号所得的参数用于实测信号。实验结果及频谱分析见图7。采用五种方法对特征信号提取后的RMSE、SNR和r见表1。通过分析图、表可知实验结果较为理想，说明该特征信号的噪声频段分布广，采用传统的低通滤波及高通滤波难以有效滤除。另外，采用传统的小波滤波方法，选取通用阈值难以有效滤除不同频段的噪声所固有的一些特征，易造成偏差，导致失真。而基于高频中值滤波的小波滤波能够有效滤除各种因素造成的干扰噪声，在重构后，原始信号的局部特征被很好地保留下来，失真更小。此组合滤波方式对于脑动脉色素浓度谱特征信号的提取是有效的。

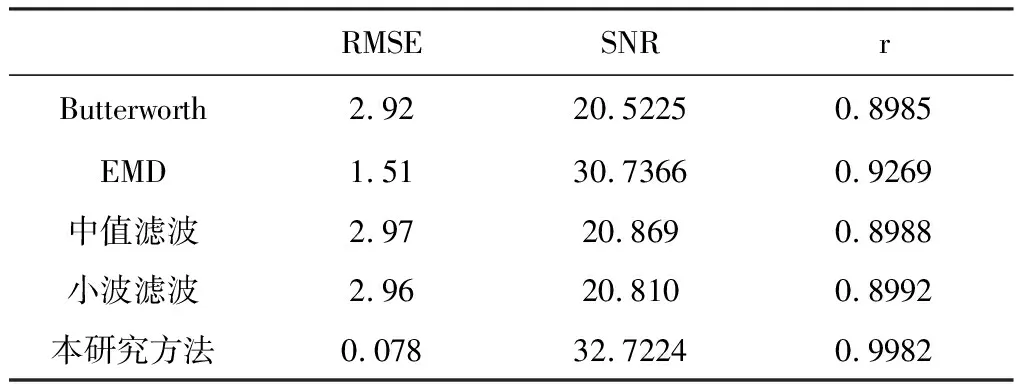
表1 种方法特征信号提取后的RMSE、SNR和r

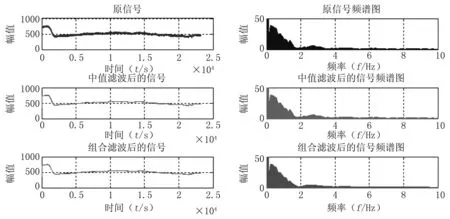
图7组合滤波效果图及频谱分析

Fig.7Combined filter effect and spectrum analysis

5 总结

基于NIRS-ICG色素浓度谱技术用于脑血流动力学参数测量，虽能建立光电容积脉搏波的模型，但其使用的常规滤波方法提取特征信号仍存在高频信号去噪能力弱、低频信号无法准确滤除的问题。为了避免上述问题，本研究提出的基于高频中值滤波的小波滤波方式，将两种已经比较完善的除噪方法结合使用，从最终的结果看，效果优于使用单个方法，具有输出信噪比高、均方差低的优势。从频谱分析图来看，各个频段的干扰都被有效滤除。但是，本研究提取出的特征信号，在低频部分仍有一部分失真有待改善。在后续的研究中，要找出低频信号失真的原因，并加以改进。本研究提供了一种新的滤波思路，为下一步的研究提供方向，希望能给其他学者提供些许参考。