可选择关联和可转换的环签名方案研究

2020-04-15濮光宁侯整风

井冈山大学学报(自然科学版) 2020年1期

关键词：匿名性公钥关联性

濮光宁，侯整风

可选择关联和可转换的环签名方案研究

*濮光宁1，侯整风2

（1. 安徽财贸职业学院，安徽，合肥 230601；2. 合肥工业大学计算机与信息学院，安徽，合肥 230009）

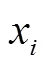
环签名；离散对数；选择关联性；可转换性；匿名性

0 前言

Rivest, Shamir和Tauman[1]在2001年首次提出环签名的概念，即签名者自主选择一些成员的公钥，其中包括签名者自己的公钥，组成一个公钥环，然后使用自己的私钥和公钥环完成签名。环签名可以成功地验证签名者属于某一个环，但却无法确定签名者的具体身份，因此，环签名可以实现无条件匿名。随着环签名概念的提出，各种环签名方案相继出现。例如Bose等人[2]提出不需要随机预言机假设的定长环签名方案，Gritti等人[3]提出O(log2n)长度的环签名方案，刘筱茜等人[4]提出多变量公钥密码体制下的环签名方案。

在某些特殊的应用环境中，例如匿名电子投票，不仅需要保证投票人的匿名性，还需要避免重复投票，这将需要用到关联环签名[5]：在环签名中添加关联标签，保证签名者匿名性的前提下，证明两个签名是否由同一个签名者所签发。第一个关联环签名方案（Linkable Spontaneous Anonymous Group, LSAG）由Liu等人[5]提出，之后出现了各种不同的关联环签名方案[6-8]。为了提高签名者的自主性，允许签名者自主决定其生成的两个环签名之间是否具备关联性，Jeong等人[9]提出了可选择关联的环签名。当为匿名者颁奖时，其匿名身份需要被揭秘，环签名需要转换成普通签名，使环签名具备可转换性。各种不同方法的可转换环签名方案[10-14]被先后出现，但大多数方案不能抵抗可转换性攻击。

1 基本概念

1.1 离散对数假设

1.2 环签名概念

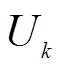
环签名需要满足以下性质：

1) 正确性。合法成员生成的环签名，可以通过签名验证算法。

环签名具备的一些特殊性质：

2) 可转换性。当需要揭秘签名者真实身份时，可以将合法的环签名转换成普通的数字签名。

2 文献[15]的方案

初始化：公开{p,q,H,H,H,L}，其中大素数是群的阶，是的产生子，是的随机数，H,H,H是哈希函数。

环签名生成：消息M，事件描述message。

3 基于离散对数的可选择关联可转换环签名方案

可选择关联可转换的环签名方案的安全性基于离散对数求解难题，包括系统初始化、环签名生成、环签名验证、可转换验证和关联性验证五个部分。

3.1 系统初始化

3.2 环签名生成

各大权威机构最新出台的政策已经指出：添加辅食不必按照固定顺序，大可放心地翻着花样来。（当然主流意见还是建议第一口辅食选择强化铁米粉，因为6个月之后母乳中的铁成分不能满足宝宝身体的需求。）

3.3 环签名验证

3.4 可转换验证

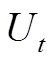
3.5 关联性验证

4 安全分析

4.1 正确性

验证等式成立，环签名正确合法。

4.2 匿名性

4.3 不可伪造性

4.4 转换性

4.5 关联性

5 性能比较

5.1 与文献[15]比较

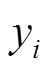
5.2 与同类方案比较

我们将本文方案与已有的可选择链接和转换的环签名方案[5,13,15]，进行性质和运算开销的比较。为了表示方便，—环成员的个数、—幂指数运算开销、—多基幂指数运算开销、—模逆运算开销，各个方案的性质和运算开销如表1所示。

表1 性质和运算开销比较

从表1可以看出，文献[5]不具有强匿名性，文献[13]和文献[15]具有强匿名性和选择关联性，但是签名开销和验证开销大于本文方案。因此，本文方案不仅提供了强匿名性和选择关联性，还具有较小的计算开销。

6 结论

本文提出的可选择关联可转换环签名方案，签名者通过自己的私钥和选取的公钥环生成环签名，通过添加随机数生成关联标签，实现选择关联性和可转换性。与同类方案相比，本文方案的计算开销相对较小，在匿名电子投票和颁奖等特殊应用中，具有良好的应用前景。

[1] Rivest R L, Shamir A, Tauman Y. How to leak a secret[C].Proceedings of ASIACRYPT’01. Berlin, Germany:Springer-Verlag,2001:552-565.

[2] Bose P, Das D, Rangan C P. Constant size ring signature without random oracle[C]. Proceedings of the 20th Australasian Conference on Information Security and Privacy(ACISP 2015). Queensland, Australia, 2015(300):230-247.

[3] Gritti C, Susilo W, Plantard T. Logarithmic size ring signatures without random oracles[J]. Information Security let, 2015,10(1): 1-7.

[4] Liu X Q, Zhao Y M. Variant scheme of ring signature based on multivariate public key cryptosystems[J]. Computer Engineering, 2015, 41(2): 96-99.

[5] Liu J K, Wei V K, Wong D S. Linkable spontaneous anonymous group signature for Ad Hoc groups[J]. Acisp, 2004:325-335.

[6] Tsang P P, Man H A, Liu J K, et al. A suite of non-pairing ID-based threshold ring signature schemes with different levels of anonymity (Extended Abstract)[C]. Proceedings of the 4th International Conference on Provable Security. Malacca, Malaysia, 2010:166-183.

[7] Au M H, Liu J K, Susilo W, et al. Secure ID-based linkable and revocable-iff-linked ring signature with constant-size construction[J]. Theoretical Computer Science, 2013(469):1-14.

[8] Sun S F, Man H A, Liu J K, et al. RingCT 2.0: A Compact Accumulator-Based (Linkable Ring Signature)Protocol for Blockchain Cryptocurrency Monero[C].European Symposium on Research in Computer Security,2017:456-474.

[9] Jeong I, Kwon J, Lee D. Ring signature with weak linkability and its applications[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(8):1145-1148.

[10] 李伟,唐明伟,范明钰. 标准模型下基于线性对的选择关联可转换环签名方案[J]. 西华大学学报:自然科学版, 2013, 32(2):1-4.

[11] Lee K, Wen H, Hwang T. Convertible ring signature[J]. IEE Proceedings Communications,2005,152(4):411-414.

[12] Hwang J Y, Chang K Y, Cho H S, et al. Collusion -resistant convertible ring signature schemes[J]. Science China Information Sciences, 2015, 58(1): 1-16.

[13] 张文芳,熊丹,王小敏,等. 基于RSA公钥密码体制的可选择可转换关联环签名[J].计算机学报, 2017, 40 (5):1168-1180.

[14] Wang H, Zhang F, Sun Y. Cryptanalysis of a generalized ring signature scheme[J]. IEEE Transactions on Dependable & Secure Computing,2009,6(2):149-151.

[15] 曹素珍,孙晗,戴文洁,等. 基于DLP的可选择链接可转换环签名方案[J]. 计算机工程, 2019,45(2):144-147.

Selectively Linkable and Convertible Ring Signature Scheme

*PU Guang-ning1, HOU Zheng-feng2

(1. Anhui Finance and Trade Vocational College, Hefei 230601, Anhui, China; 2. School of Computer and Information, Hefei University of Technology, Hefei 230009, Anhui, China)