土壤残膜对水分入渗过程的影响

曹俊豪，李援农，谷晓博，陈朋朋

(西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌 712100)

地膜覆盖技术在我国被广泛应用于农业中[1,2]，目前地膜覆盖主要两种覆盖方式为地表覆盖地膜和垄上覆膜。据研究，地表覆盖地膜可以保水保墒[3,4]、减少土壤水分蒸发[5-7]等作用，垄上覆膜可以减少地表水分蒸发，提高缺水地区对地表水的利用效率，同时还能起到增加地表温度促进作物出苗、改善土壤结构等作用。但是，由于地膜覆盖在长期使用过程中，导致残膜留存于土壤中的含量不断增加，导致地膜使用地区粮食产量逐渐衰减，因此探究土壤残膜含量与埋深对水分垂直入渗过程的影响对于促进粮食增产和节约水资源具有深远意义。

李仙岳[8,9]研究发现湿润体和湿润锋运移距离和残膜量呈负相关，随残膜量的增加而减小。王志超[10]研究认为，随着土壤含水率和残膜埋深的增加，土壤湿润体的面积逐渐缩小。邹小阳[11]研究认为，水平湿润锋运移速率、土壤含水率和累积入渗量均随残膜量增加而减小。李元桥等[12]研究认为湿润锋运移会受到残膜的阻碍作用，当湿润锋在10～20 cm和0～10 cm土层之间会存在差异。解红娥等[13]研究认为土壤体积质量随残膜量的增加逐渐增加，呈对数递增关系，残膜量与土壤水分运移速率呈负相关。党雪瑞等[14]研究认为，相对体积质量随残膜量增加而增大，土壤体积质量与残膜量呈正相关，而土壤孔隙度和含水率则随残膜量的增大而减小。前人关于残膜含量与残膜埋深对土壤入渗的影响进行了一系列研究，但多集中于残膜含量和残膜埋深等单因素与湿润锋运移时间之间的关系，而关于残膜含量、残膜埋深、土壤干容重和初始含水率双因素间的互作效应对湿润锋运移时间的影响研究不足。

本文主要结合前人的研究成果，通过四元二次正交旋转组合试验，研究残膜量、初始含水率、残膜埋深和土壤干容重对土壤湿润锋运移时间的影响，并通过双因素间的互作效应分析研究双因素对湿润锋运移时间的影响，旨在为残膜污染区下的合理灌溉制度提供理论基础。

1 材料与方法

1.1 试验设计

试验采用二次旋转回归正交设计，设置土壤初始含水率、土壤干容重、残膜量、残膜埋深4个试验因素，每个因素设置5个水平。配置土壤初始含水率(取质量为M的样土)所需加水量：

式中：m为样土总重量；ω为初始含水率，%。

每层土柱加土质量：

M1=πr2hPb(ω+1)

式中：Pb为土壤干容重，g/cm3；h为每层土的高度，cm；r为土层半径，cm；其余符号意义同前。

试验因素及水平见表1。

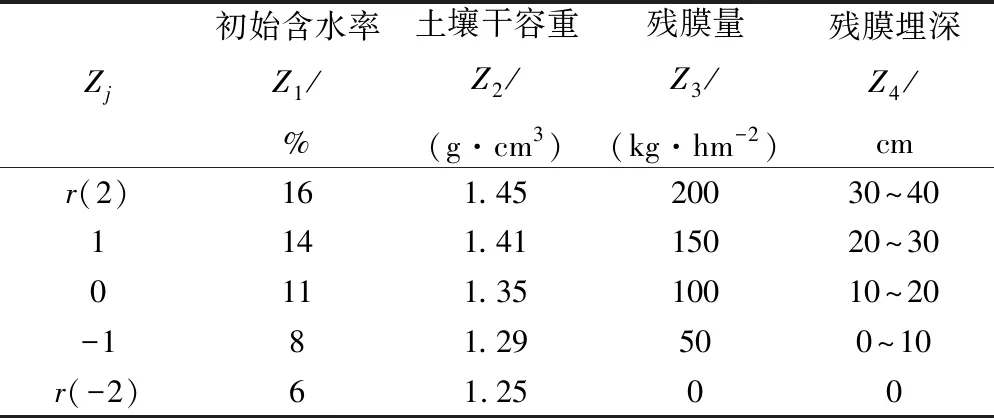
表1 试验因素及水平

装土前先在土柱壁上涂抹凡士林，避免产生优势流；每 5 cm分一层装土，层与层之间需打毛；试验开始前，在土壤表面放半径为12 cm的滤纸，防止水流冲刷表层，试验开始将滤纸拿出。分别记录入渗时间为1、2、3、4、5、6、7、8、9、10、15、20、25、30、35、40、60、80、100、120、140…580、600、620 min时的湿润深度，当土壤湿润锋运移到40 cm时，结束试验，记录总运移时间。土柱面积较小，为避免残膜的大小对土壤垂直入渗的影响，将残膜大小统一控制为2 cm×1 cm的长方形，每层装土之前将定量的土壤与残膜放入搅拌机，使其搅拌均匀，残膜随机分布所在层。

1.2 试验方案

本实验采用二次旋转回归正交组合设计试验，四因素五水平共36个组合，各组合重复一次实验，湿润锋运移时间取均值，各因素的水平编码表见表1，实验方案见表2。

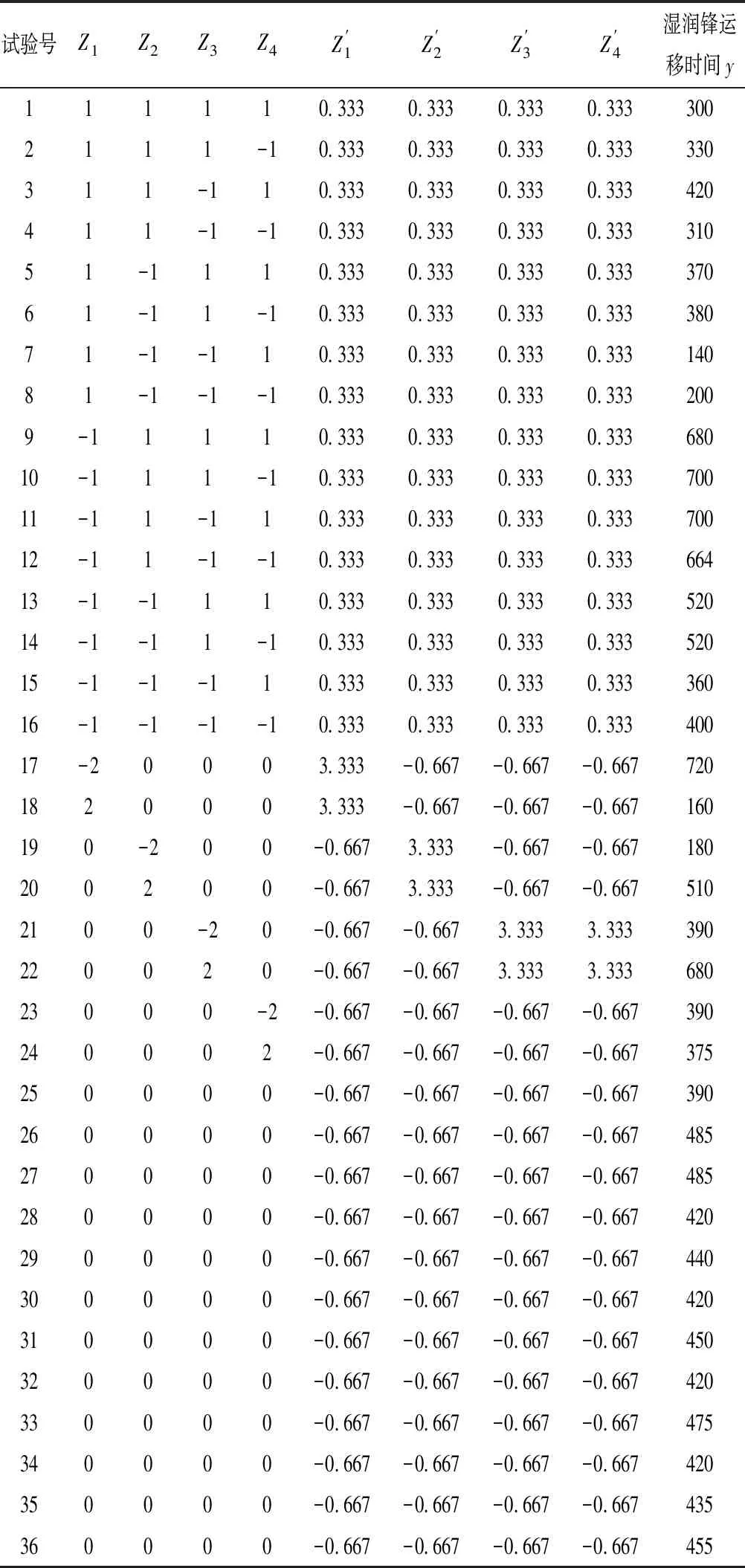
表2 二次回归正交旋转组合设计

采用Matlab软件对实验结果进行分析，生成三维图形，并用Excel处理试验方程统一绘制图标。

1.3 试验装置与方法

试验在陕西省杨凌区西北农林科技大学试验站内进行(N34°18'，E 108°24')，位于中国西北黄土高原南部，海拔512 m，是典型的旱地农业区，该地区地势平坦，地下水埋深80 m，光照资源丰富。本试验土壤取自试验站内试验田表层土，实验土壤质地为壤土，将实验土去除石子等杂质后风干，用碾压机碾压，碾压后放在阳光下暴晒，然后通过5 mm筛网备用，测得暴晒后的土壤含水率为2.02%。土壤基本性质见表3，供试地膜，厚度为0.008 mm。

试验装置如图1所示，其中在土柱底端1 cm处有一个排气孔，用于土壤入渗过程中排除土壤内部空气，消减入渗过程空气压力对湿润锋运移的影响。用石英石将土柱最低端5 cm填充；在石英石上端5 cm放入沉降土(土壤容重为1.35 g/cm3)，防止试验过程中，上层土壤进入石缝内；沉降土上层装40 cm实验土，实验土共分四层及0～10、10～20、20～30、30～40 cm；分别在土壤表层以下5、15、25、35 cm处钻两个r=1 cm的圆孔，入渗结束以后，及时从圆孔内取土，测量含水率，试验期间则用橡胶塞封闭防止漏水；实验土装土时，每5 cm装一次土，层与层之间需打毛。其中试验所用马氏瓶和土柱均选用半径r=12 cm的有机玻璃制成，马氏瓶高80 cm，土柱高70 cm，在入渗过程中入渗水头保持6 cm不变。

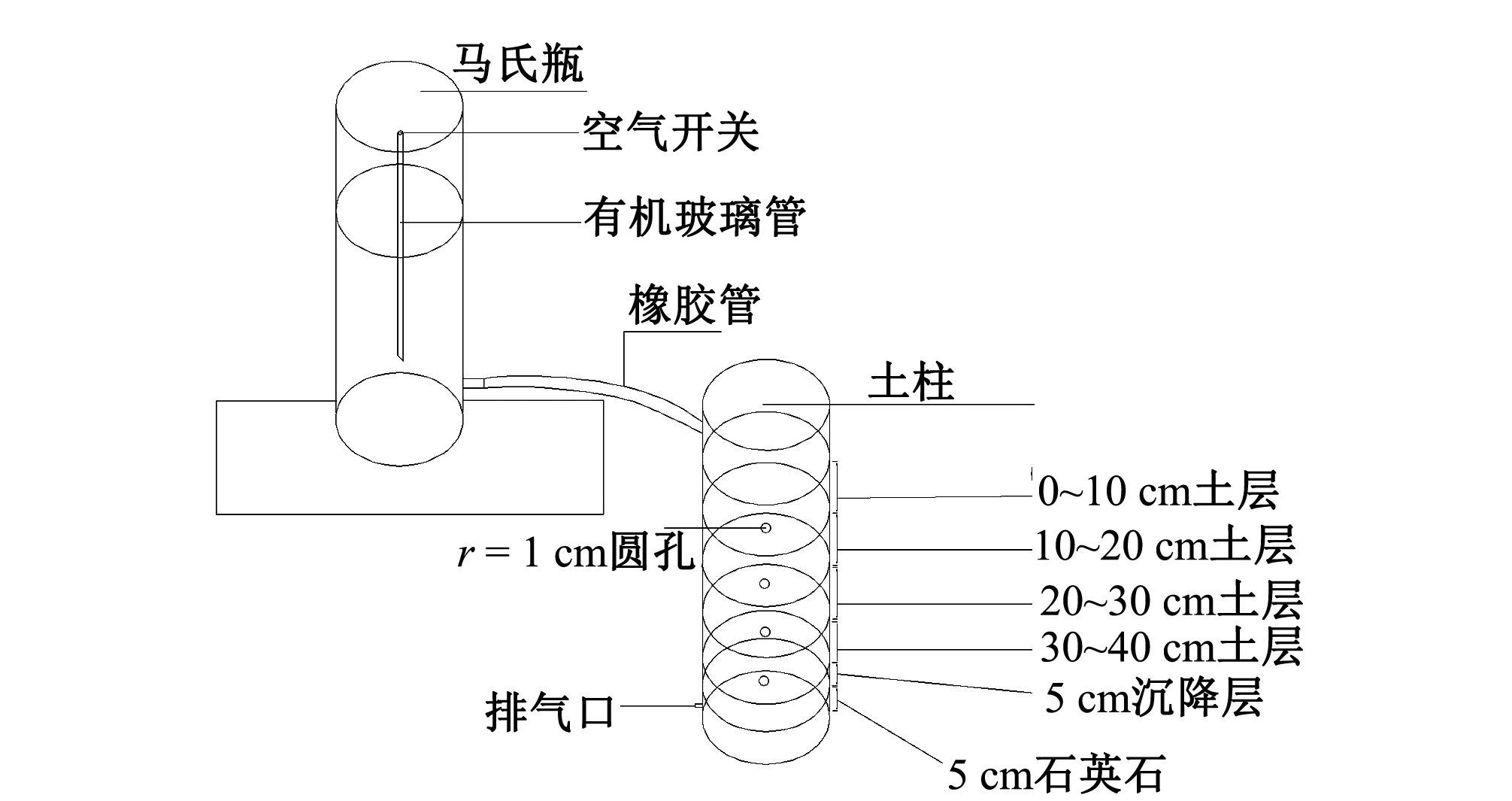
图1 试验装置示意图

表3 土壤基本性质

2 结果与分析

2.1 试验数据分析方法

2.1.1 当有p个变量时，二次回归方程的一般形式为：

(1)

(1)bj的计算。

其中n表示试验的组数：

(2)Bj的计算。

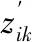
2.1.2 回归方程的检验

(2)

(1)剩余平方和为：

(2)回归平方和：

(3)总平方和：

2.1.3 方程拟合度检验

(3)

(1)误差平方和由零水平检验结果获得：

式中：m0为零水平试验次数。

(2)失拟平方和：

QLf=Qe2-Qe,fLf=fe2-fe

2.2 结果分析

根据实验结果和计算方法，得到土壤湿润锋运移时间与残膜埋深、初始含水率、残膜含量、土壤干容重的二次回归模型为：

Y=441.25-133.927Z1+78.08Z2+49.42Z3-1.83Z4+

0.88Z1Z3+2.13Z1Z4-48.38Z2Z3+12.88Z2Z4-6.63Z3Z4

(4)

回归方程的检验：

(5)

结果表明回归方程是极显著的。F在0.01水平上显著，说明实验所选四因子对土壤湿润锋运移时间有显著影响。

拟合度检验为：

(6)

结果显示回归方程拟合度高。

对二次模型进行方差分析，结果表明初始含水率、干容重和残膜含量的一次项和残膜含量的二次项以及初始含水率和干容重的交互项、干容重和残膜量的交互项、残膜埋深二次项均达到显著水平(P<0.05)，其余互作均不显著(表3)。因此，在P=0.05的显著水平，简化后的回归方程为：

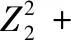
(7)

2.3 主因素效应分析

由各回归系数的显著性水平可知，初始含水率、土壤干容重和残膜含量三个因素达到显著水平，表明残膜埋深对湿润锋运移时间影响不明显，而残膜含量、初始含水率、土壤干容重是影响土壤湿润锋运移时间的主要因素。

由于设计采用正交设计，并且各因素均经无纲量进行编码处理，所有回归系数间都是相互独立的，因此对土壤湿润锋运移时间的影响可以用各因素一次项回归系数的绝对值大小进行比较，影响土壤湿润锋运移时间大小顺序为：初始含水率>土壤干容重>残膜含量(133.92>78.08>49.42)。

2.4 单因素效应分析

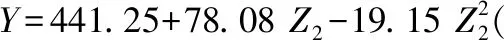
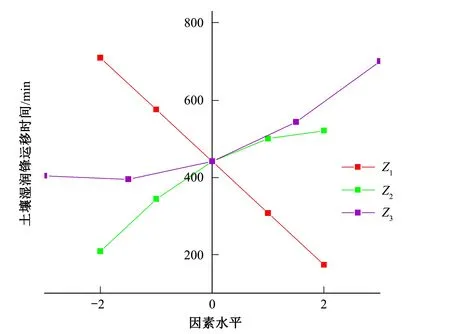
图2 湿润锋运移时间与各因素的关系曲线

2.5 双因素间的互作效应分析

由表3中P显著性检验结果可知，残膜含量与土壤干容重和初始含水率与土壤干容重双因素间互作效应(p<0.05)。去除残膜含量项后，得出土壤湿润锋运移时间与初始含水率和土壤干容重的关系方程式为:

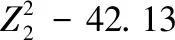
利用Matlab对初始含水率与土壤干容重间的互作效应作三维图形(图3)，由图3可知，当初始含水率大于11%时，随着土壤干容重的增加湿润锋运移时间先增大后减小；当初始含水率小于11%时，随着土壤干容重的增大湿润锋运移时间逐渐增大。这可能由于初始含水率越高，累积入渗量越小，即相同时间对应水量较少[15]。因此，要想让湿润锋运移时间最短，要尽量保持土壤含水率较大和土壤干容重较小。当土壤干容重较小时，随着初始含水率的增大，湿润锋运移时间减小较慢；当土壤干容重较大时，随着初始含水率的增加，湿润锋运移时间减小较快。这可能因为土壤干容重越大，土壤内的孔隙率越小，对水分运动的阻塞作用越大。

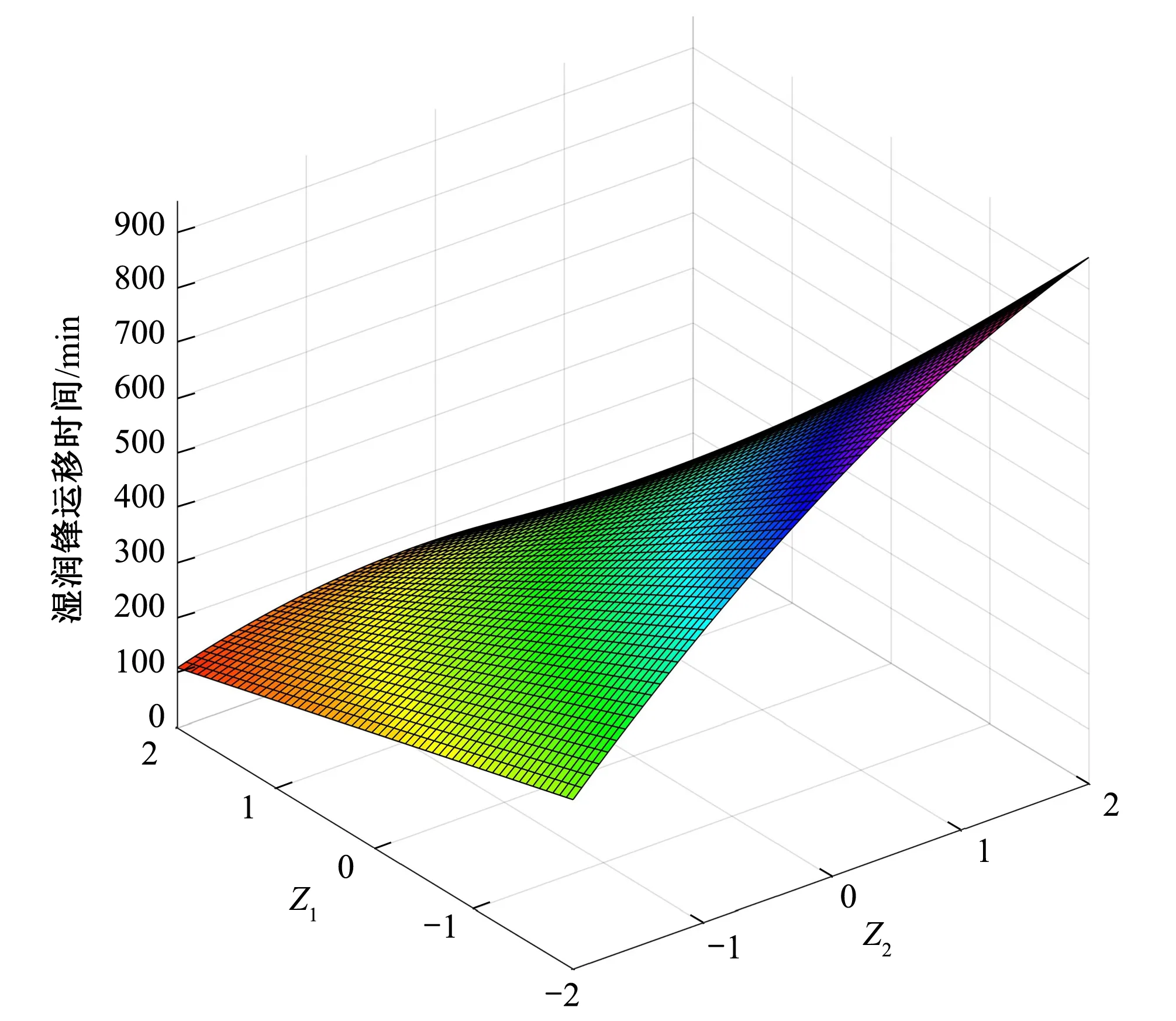
图3 初始含水率-土壤干容重互相应曲面

将含初始含水率项去除之后，得出土壤湿润锋运移时间与土壤干容重和残膜含量与的方程式为：

利用Matlab对土壤干容重和残膜含量间的互作效应作三维图形(图4)，由图4可知，当土壤干容重小于1.41 g/cm3时，湿润锋运移时间随残膜含量的增长而增长；当土壤干容重大于1.41 g/cm3时，湿润锋运移时间随残膜含量的增长反而减小。当残膜量小于150 kg/hm2时，湿润锋运移时间随土壤干容重的增加而增大；当残膜量大于150 kg/hm2时，湿润锋运移时间在残膜含量的变化下保持稳定趋势。

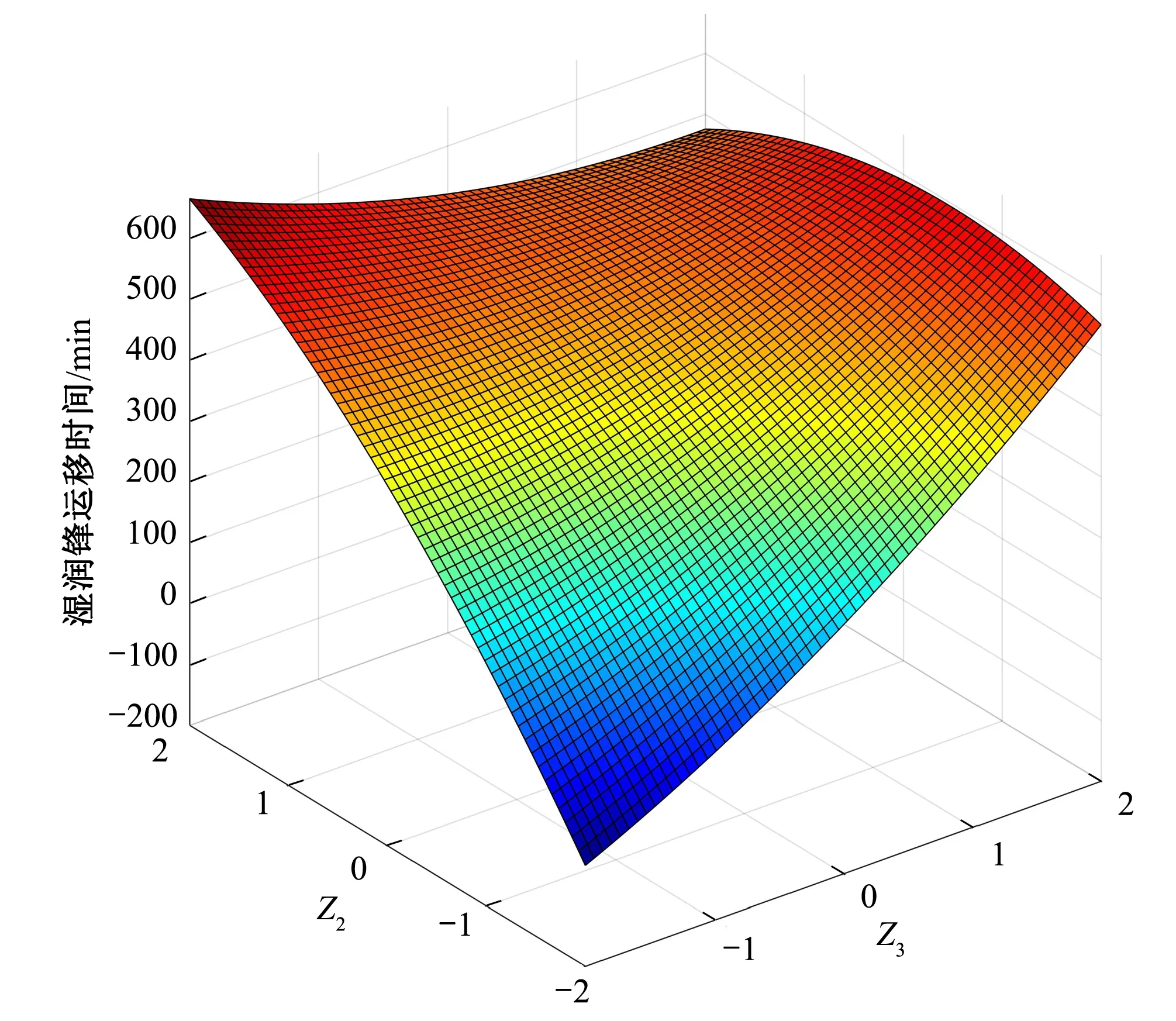
图4 土壤干容重-残膜量互相应曲面图

3 讨 论

本试验通过二次旋转组合正交试验研究残膜含量、残膜埋深、初始含水率、土壤干容重与湿润锋运移时间之间的关系，研究结果表明，残膜含量、初始含水率、土壤干容重与湿润锋运移时间之间显著相关，残膜埋深与湿润锋运移时间之间不显著，而李元桥[12]研究认为湿润锋在0～10和10～20 cm土层之间存在明显差异，王志超[10]研究结果表明湿润锋水分入渗曲线受残膜埋深的影响比较大。这可能是因为本试验在试验过程中土柱里土壤空气压力保持恒定，再加上入渗过程中水头一直保持6 cm不变，湿润锋下移速度较快，所以可能导致了湿润锋运移时间与土壤中残膜的埋深不显著。

土壤湿润锋运移时间随残膜量的增加而减小，残膜对土壤湿润锋垂直下移具有一定的阻塞作用，邹小阳的试验结果与此结论一致[11]。初始含水率与湿润锋运移时间呈负相关，这是由于，土壤初始含水率越高，土壤中孔隙含量较小，导致累计入渗量越变少，即相同入渗时间对应入渗水量变少，所以湿润锋运移时间变短；土壤干容重与土壤湿润锋运移时间呈负相关，这是由于干容重越大，土壤颗粒间孔隙越小，对土壤水分运移的阻塞作用越大，所以与湿润锋运移时间呈正相关。但是随着干容重的增大，土壤孔隙率变小，干容重对土壤入渗的影响也变小，所以湿润锋推进也会变慢，这与李援农[16]的研究结果一致。

双因素间的互作效应分析显示，当初始含水率大于11%时，随着土壤干容重的增加湿润锋运移时间先增大后减小；当初始含水率小于11%时，随着土壤干容重的增大湿润锋运移时间逐渐增大。当土壤干容重较小时，随着初始含水率的增大，湿润锋运移时间减小较慢；当土壤干容重较大时，随着初始含水率的增加，湿润锋运移时间减小较快。当土壤干容重小于1.41 g/cm3时，湿润锋运移时间随残膜含量的增长而增长；当土壤干容重大于1.41 g/cm3时，湿润锋运移时间随残膜含量的增长反而减小。当残膜量小于150 kg/hm2时，湿润锋运移时间随土壤干容重的增加而增大；当残膜量大于150 kg/hm2时，湿润锋运移时间在残膜含量的变化下保持稳定趋势。这是由于残膜是随机分布在土壤内的，当残膜在土壤中处于垂直或者倾斜状态是，水分可以顺着残膜的光滑作用进行下移；而当残膜量较大的时候，残膜与残膜之间形成致密的组断层，阻止水分下移。如上所述，残膜对土壤湿润锋下移具有一定的阻塞作用，在一定条件还具有导流作用，当残膜量大于150 kg/hm2时，随着土壤容重的增加，湿润锋运移时间保持稳定趋势。

4 结 语

(1)初始含水率、土壤干容重和残膜含量与湿润锋运移时间显著相关，而残膜埋深与湿润锋运移时间不显著，影响土壤湿润锋运移时间大小顺序为：初始含水率>土壤干容重>残膜含量(133.92>78.08>49.42)。

(2)随着土壤干容重和残膜量的增加，湿润锋运移时间也在逐渐增加，随着初始含水率的增加，湿润锋运移时间反而直线减小；而湿润锋运移时间增长速率随干容重的增加而减小。

(3)交互效应分析显示：当土壤干容重小于1.41 g/cm3时，随着残膜量的增加，湿润锋运移时间增长；当土壤干容重大于1.41 g/cm3时，随着残膜量的增加，湿润锋运移时间反而减小。当残膜量小于150 kg/hm2时，随着土壤容重的增加，湿润锋运移时间增大；当残膜量大于150 kg/hm2时，随着土壤容重的增加，湿润锋运移时间趋于稳定。

□