超长航时太阳能无人机关键技术综述

2020-04-15马东立张良杨穆清夏兴禄王少奇

航空学报 2020年3期

马东立，张良，杨穆清,*，夏兴禄，王少奇

1. 北京航空航天大学航空科学与工程学院，北京 100083 2. 西安现代控制技术研究所，西安 710065

超长航时太阳能无人机利用太阳能电池将光能转化为电能，一部分用于日间巡航，另一部分储存在储能电池中，用于夜间巡航，从理论上打破了常规无人机所无法实现的“永久”飞行的瓶颈，从而成为近年来无人机领域研究的热点[1-3]。此类无人机具有无污染、航时长的特点，可广泛应用于对地观测、空中预警、侦察监视、通讯中继等军事和民用领域[4]。与卫星相比，其信号传输损失小、精度高，可实现目标区域永久驻留，不存在重返周期问题，生产和运营成本低；与传统飞机相比，其覆盖区域广，留空时间长；与浮空器相比，其操控性好，机动性强。未来战争中，超长航时太阳能无人机将在空间攻防和信息对抗中发挥重要作用，成为空中力量的重要补充，进一步促进空天一体化发展[5]。

自1974年“Sunrise-Ⅰ”太阳能无人机[6]问世以来，各国在太阳能无人机领域取得了多项突破。美国NASA致力于飞翼太阳能无人机研制，经历了“Pathfinder”“Centurion”“Helios”等多个阶段，翼展从“Pathfinder”的30.5 m增大到“Helios”的75.3 m[7-8]，“Helios”在2003年试飞中达到了29.5 km的最大飞行高度；瑞士联邦理工学院研发的“Atlantiksolar”[9-10]是一台质量只有6.8 kg的小型太阳能无人机，该无人机于2016年7月完成长达26 h的难民搜救任务，全程无人工干预，为搜救团队及时反馈了重要信息；中国航天空气动力研究院研发的“彩虹”太阳能无人机[11-12]具备20 kg载荷能力，于2017年完成临近空间飞行试验，飞行高度超过20 km；英国于2003年启动了“Zephyr”系列太阳能无人机研制，2018年7月，“Zephyr-S”无人机创造了26天不间断巡航的新记录[13]；UAVOS推出的“ApusDuo”太阳能无人机采用了串列翼布局，2018年5月，该公司宣布已顺利完成14 m翼展原型机的飞行试验。近年来，越来越多国家和组织报道了各自的太阳能无人机研制情况，这些太阳能无人机呈现出飞行时间越来越长，载荷能力越来越强的特点(见表1)。

太阳能无人机升阻比高、飞行速度低，机翼具有超大展弦比和较低翼载荷，设计指标与能量参数深度耦合，尤其是临近空间太阳能无人机，其飞行高度高、载荷能力弱的特点尤为突出，对总体、气动、结构、飞控、能源、推进以及航迹设计带来很大难度。本文对超长航时太阳能无人机涉及的总体设计技术、气动设计技术、气动弹性与阵风减缓技术、飞行控制技术、高效能源技术、动力推进技术、轨迹优化技术等7项关键技术的研究现状及相关文献进行综述，并对未来发展进行了展望。

表1 太阳能无人机设计参数及试飞数据Table 1 Design parameters and flight test data of solar powered unmanned aerial vehicle (UAV)

1 总体设计技术

相比于常规无人机，超长航时太阳能无人机总体设计需要耦合更多因素，如翼面积不仅影响气动性能，也与能量获取能力密切相关，设计过程须综合考虑太阳能光照、太阳能电池/储能电池等因素，设计方法相对特殊。

文献可见最早的太阳能无人机总体设计方法由Youngblood等[14]在1984年提出，如图1所示，其基本思路是通过对比由能量平衡公式得到的CL1.5/CD需用值及由气动力公式得到的CL1.5/CD计算值是否与飞机尺寸匹配，来判断总体设计参数是否可行，再通过迭代得到总体设计参数。而后，Brandt和Gilliam[15]建立了一种基于约束分析的太阳能飞机总体设计方法，如图2所示，该方法的核心思路是构建以翼载荷为横坐标、以太阳能电池铺片面积与机翼参考面积比值为纵坐标的约束图，根据飞机设计需求在约束图中划定可行域，再从可行域中选择设计点。2种方法本质上都是基于能量平衡和质量平衡方程，结合飞行动力学方程展开的，区别在于，Youngblood方法得到的是设计点，相对较精确，而Brandt方法得到的是可行域，参数选取灵活性更高。2种方法为后来的学者研究更为完善的总体设计流程提供了框架。

图1 Youngblood 总体设计流程[14]Fig.1 Youngblood overall design process[14]

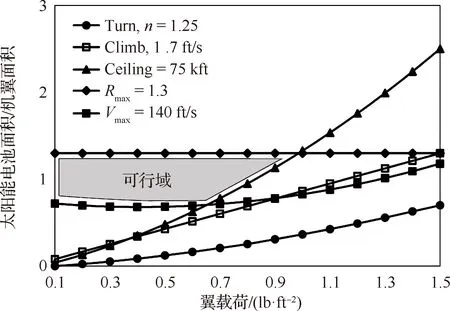
图2 Brandt 总体设计流程[15]Fig.2 Brandt overall design process[15]

Noth[16]在Youngblood设计方法的基础上，对质量和能量估算公式进行细化，提出了一套更为完善的总体设计方法,如图3所示，后人在设计太阳能无人机时对这种方法借鉴较多。Noth的方法经过了“Sky Sailor”太阳能无人机的飞行验证，适用于从起飞质量1 kg以内的小型太阳能无人机平台到翼展数十米的大型太阳能无人机平台的设计。文献指出，太阳能无人机设计主要基于能量平衡方程和质量平衡方程对其平飞速度和机翼面积进行解算。此外，文献还统计出了62 架太阳能无人机的起飞质量和翼载荷的关系，可利用这一关系验证设计的太阳能无人机是否合理。

Romeo等[17-18]详细说明了HELIPLAT太阳能无人机的设计流程，研究了根梢比、翼梢形状、拐点位置对机翼气动特性的影响，得到了阻力估算方法，进而得到了功率面积比的计算方法，并采用CFD方法对全机气动特性进行了分析。文献虽然没有提到具体的参数估算方法，但提出了参数估算时必要的气动特性估算方法、结构重量估算方法，并对大展弦比机翼结构设计进行了说明，具有一定借鉴意义。此外，文献[19-21]介绍了不同太阳能无人机的完整设计流程，其总体设计方法大同小异，本质上都是基于能量平衡和质量平衡的迭代设计。

近10年来，太阳能无人机总体设计方法得到了进一步完善和细化。Maleki[22]在Brandt设计方法的基础上，进一步引入了“技术水平”参数的概念，该参数表征的是载荷重量与全机重量的比值，可用于太阳能无人机起飞重量和机翼参数的估算过程。Morrisey和Mcdonald[23]开发了超大展弦比太阳能无人机的多学科优化设计方法，在创建分析模块时，根据已知数据进行了验证和校准，最终对集成的优化程序进行了验证。

图3 Noth 总体设计流程[16]Fig.3 Noth overall design process[16]

国内方面，昌敏等[24]开展了太阳能飞机总体设计方法研究，其阐述了太阳能飞机飞行原理，建立了太阳能飞机总体设计模型，并采用敏度分析的方法，着重分析了各总体参数对太阳能飞机可持续飞行高度的影响及约束程度，研究表明，光伏组件效率及其面密度、结构面密度及二次电池比能量是约束可持续飞行高度的主要因素。曹青等[25]建立了由“建立能量链”“建立质能关系”“连接总质量和能量链起点完成迭代环”三步组成的不间断飞行太阳能无人机总体参数设计的一般方法,设计流程如图4所示。该方法在考虑气动布局参数的基础上，完善了气动参数估算方法，相比Noth的总体设计方法，拓展了设计域，增强了设计方案的负载能力。

王少奇[26]在总体设计阶段将约束条件进行了简化，如图5所示，区域A代表了能量平衡约束，区域B代表了质量平衡约束，两者相交的区域C即无人机质量m和机翼面积S的可行域，当2个平衡方程均取等号时，m和S同时取到最小值，即无人机的临界平衡点。此外，文献还对不同设计高度太阳能无人机的质量和机翼面积可行域展开研究，如图6所示，随夜间飞行高度增大，临界平衡点对应的无人机质量和需用机翼面积逐渐增大，上下边界曲线的夹角减小，可行域缩小。当飞行高度超过一定值后，可行域急剧减小，直至不存在。

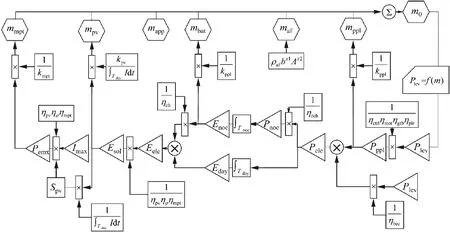
图4 基于“能量链”的总体设计流程[25]Fig.4 Conceptual design process based on “energy chain”[25]

图5 太阳能无人机质量和机翼面积的可行域[26]Fig.5 Feasible region of mass and wing area of solar powered UAV[26]

图6 不同设计高度的无人机质量和机翼面积可行域[26]Fig.6 Feasible regions of mass and wing area of solar powered UAV at different design altitudes[26]

张芳等[27]基于Noth的总体设计方法，在设计流程中引入了任务载荷性能指标，提出了一种特种太阳能飞机初步方案设计方法；赵辉杰和马建超[28]以太阳能无人机的持久飞行能力为目标分析了太阳能电池片、蓄电池、气动布局效率等因素的综合影响；张秦岭等[29]在太阳能飞机总体设计框架中引入了重力储能概念，建立了蓄电池重量比的关系公式，该总体设计方法可简化机载能源系统关键参数计算过程；张健和张德虎[30]进一步分析了临近空间长航时太阳能无人机总体设计中的动力装置匹配性、布局选型、飞行剖面优化和使用环境影响等问题；李赛等[31]在总体设计阶段引入了大气质量和大气透明度系数，用直接辐射强度和散射辐射强度建立了太阳能无人机的太阳辐射模型，更准确地表征了太阳辐射强度，同时提出了“跨夜剩余航时”的概念，以此来衡量太阳能飞机跨夜能力的高低。

2 气动设计技术

2.1 低雷诺数空气动力学

航空领域，低雷诺数的范围被定义为104～105量级[32]。太阳能无人机的低巡航速度及飞行环境的低空气密度决定了其具有明显的低雷诺数特性，存在诸多特殊流动现象[33-35]。

现有文献表明，低雷诺数现象的主要特征有2种。其一是翼型气动效率随雷诺数降低产生的急剧恶化(图7)，当雷诺数小于3×105时，翼型升阻比CL/CD开始剧烈下降，直到雷诺数降至105附近，此时升阻比仅为常规雷诺数下的10%左右；随后，翼型气动效率随雷诺数降低开始较为缓慢地下降[36]。这一特征是低雷诺数效应影响太阳能无人机的核心因素,会导致全机升阻特性的恶化和螺旋桨推进效率的下降，同时也会对舵面操纵特性和操纵效率产生影响。其二是低雷诺数下翼型气动特性随迎角α变化产生的非线性效应。这一效应主要包括3种现象，一种是对称翼型在小迎角附近出现小平台甚至“S”形弯曲(图8)[37]，随着雷诺数增加，平台会逐渐缓解并消失。研究表明，非对称翼型不会出现此类现象。另外2种现象分别是中大迎角下顺时针和逆时针静态滞回效应[38]。如图9所示，MILEY翼型为逆时针方向,而LISSAMAN翼型升力曲线为顺时针方向。试验表明，随着雷诺数的增加，滞回现象也得到缓解并消失。

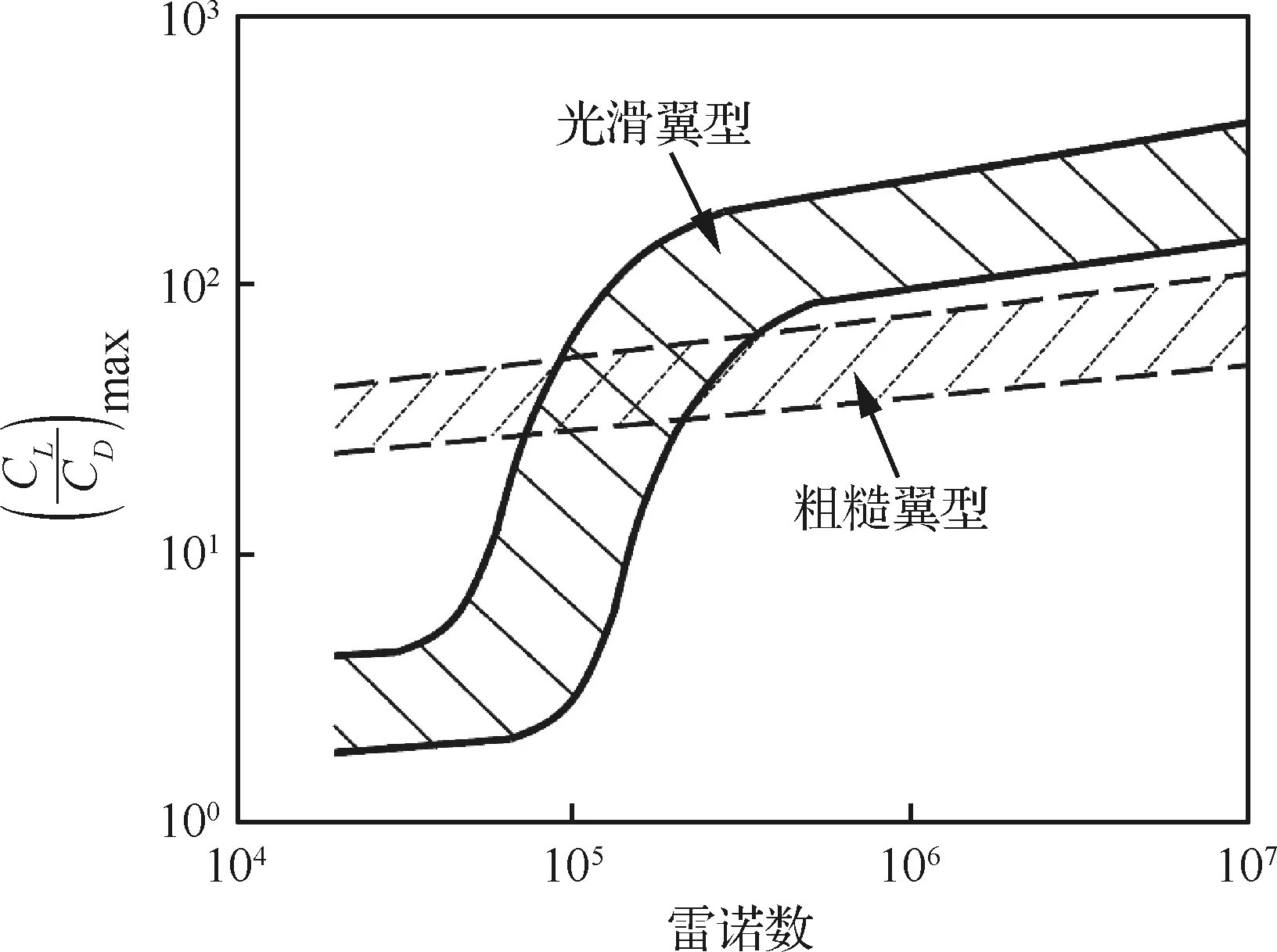
图7 低雷诺数翼型性能[36]Fig.7 Low Reynolds number airfoil performance[36]

研究表明，上述2种特殊现象的成因与层流分离泡随雷诺数和迎角变化过程中层流诱导分离的触发和演化机制有关[33]，前人已对层流分离现象进行了深入研究。

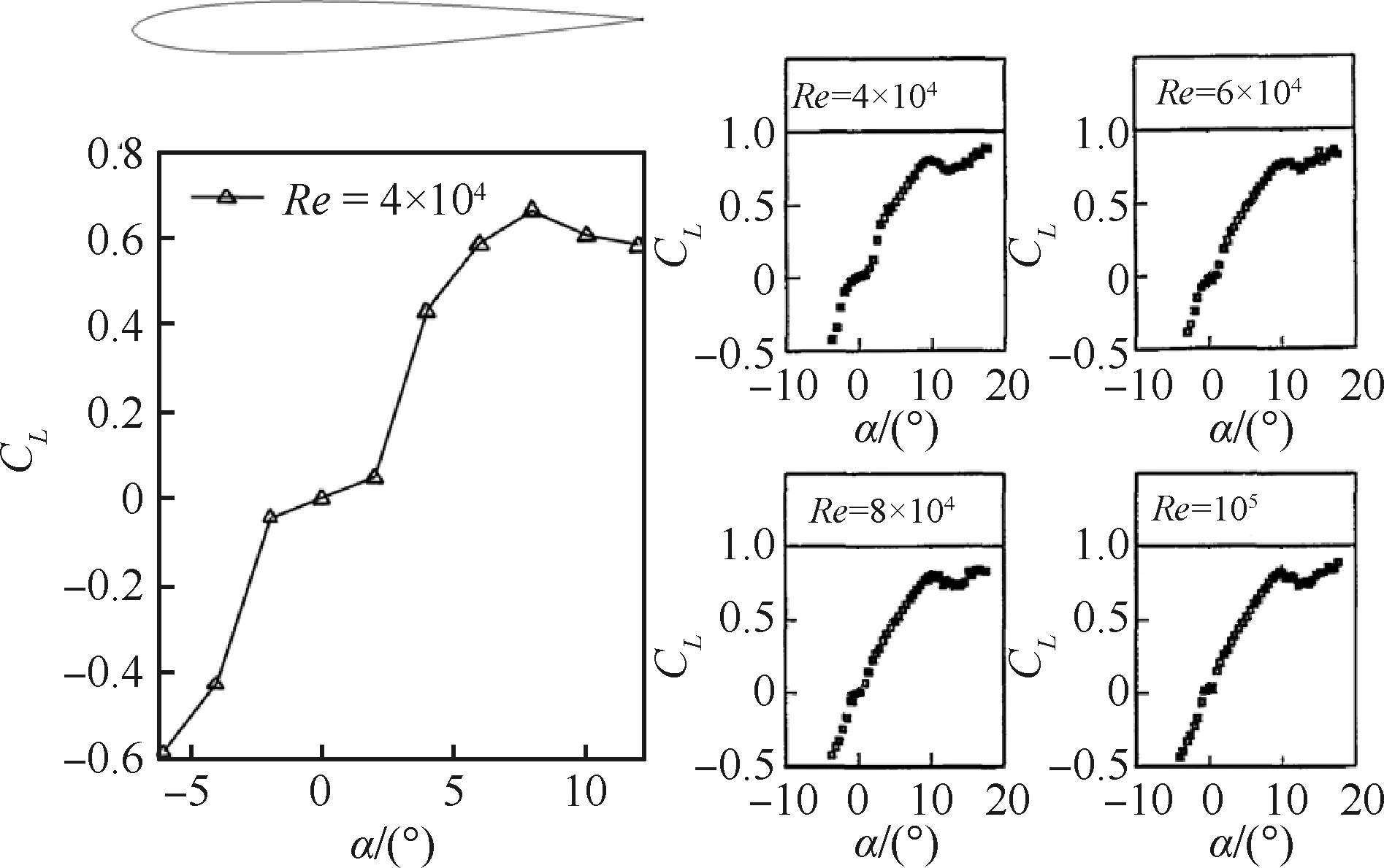
图8 对称翼型SD8020在不同雷诺数下的升力曲线[37]Fig.8 Lift curves of symmetric airfoil SD8020 at different Reynolds numbers[37]

图9 低雷诺数静态滞回现象[38]Fig.9 Static hysteresis at low Reynolds number[38]

Gaster[39]通过在平板上方安装不同翼型来构造不同的逆压梯度，进而观察和研究平板上的层流分离现象；Horton[40]则基于试验研究了分离泡的形成机理和涡系结构，并开展了基于试验的半经验公式的理论研究工作。Gaster和Horton的研究奠定了低雷诺数层流分离问题的基础，形成了经典的层流分离泡理论，如图10所示，即：当附面层中流体无法克服逆压梯度继续前进时，层流脱离壁面产生分离，进而转捩形成湍流，湍流更剧烈的微尺度动量交换将外界能量引入，使分离的边界层重新获得足够动量，形成再附。

Mueller和Batil[38]采用烟丝法对低雷诺数下二维翼型分离现象进行了研究，认为长气泡分离是在特定雷诺数下由短气泡破裂形成的(文献[41]认为这种描述是不恰当的)，并指出静态滞回方向性与长气泡分离和短气泡分离的演化顺序相关。Pauley和Moin[41]着重研究了分离泡的非定常特性，通过求解非定常不可压Navier-Stokes方程，分析了非定常情况下雷诺数和迎角对分离泡的影响。Liebeck[42]则将试验方法得到的低雷诺数翼型分离泡结论运用于翼型设计。

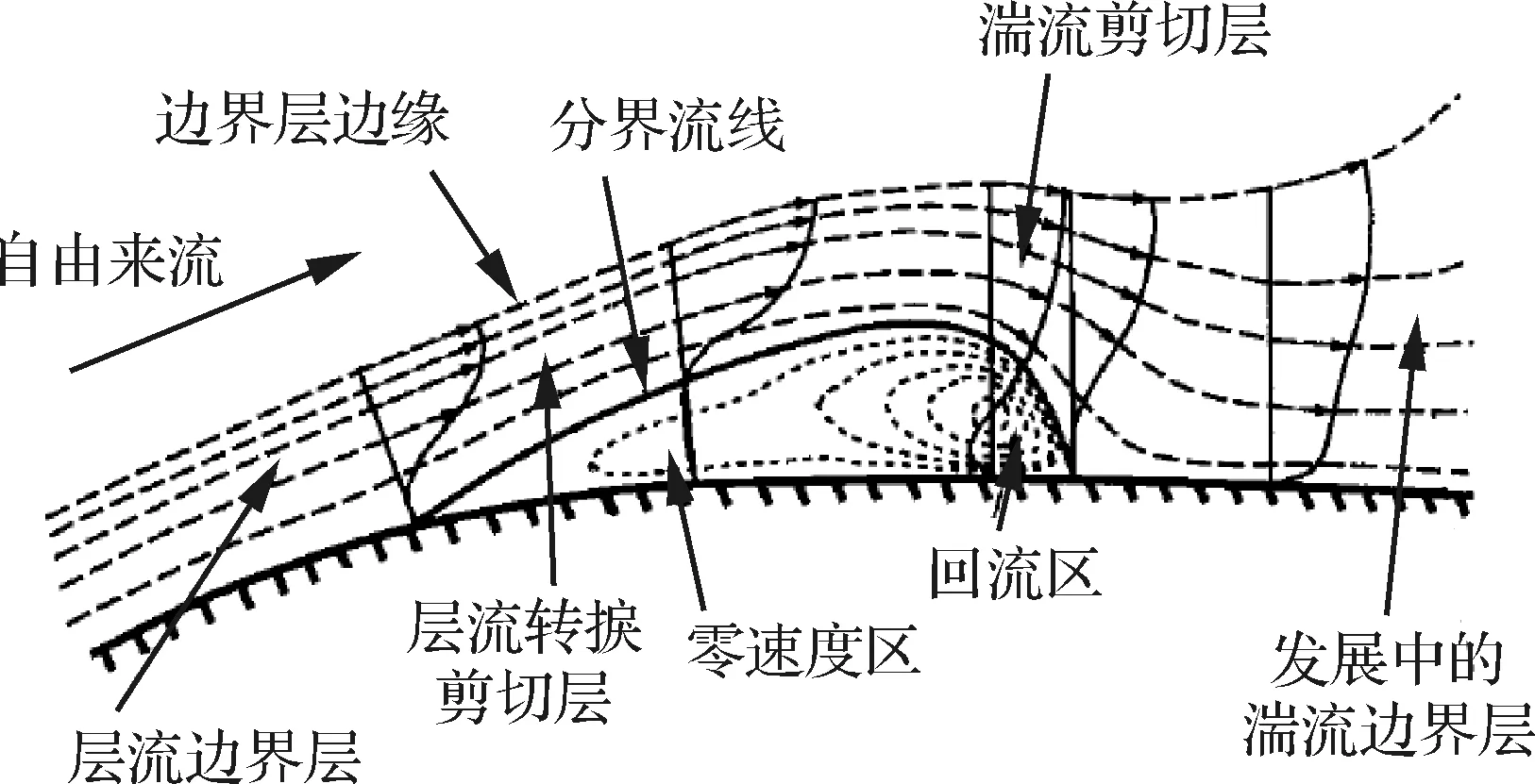
图10 Horton经典二维层流分离泡模型[40]Fig.10 Horton classical two-dimensional laminar separation bubble model[40]

事实上，随着研究的深入可以发现经典理论描述的层流分离泡并不存在，低雷诺数流动本质是一种非定常流动，而经典层流分离泡是这种非定常流动的时均化结果，尽管如此，经典层流分离泡理论仍是指导低雷诺数流动研究的基础[32]。

近年来，中国学者对低雷诺数问题进行了大量数值计算和试验研究，对低雷诺数流动理论进行了完善和拓展。白鹏等[33，43]用数值方法研究了低雷诺数层流分离的非定常和时均化特性,对漩涡脱落中主涡、二次涡以及出现的漩涡的周期性过程和对气动力脉动造成的影响进行了较为细致的研究，并在研究过程中发现了一种新的流动结构，即后缘层流分离泡结构，经典层流分离泡主要使阻力增加，而后缘层流分离泡不仅会使阻力增加，还会使升力大幅下降；冉景洪等[44-45]研究了低雷诺数下翼型的最大相对厚度、最大相对厚度位置及最大弯度对翼型等速上仰时的动态气动力影响；刘强等[46]采用非定常数值模拟和低雷诺数风洞流动显示技术相结合的方法，对FX63-137翼型不同雷诺数、不同迎角下的流动特性展开研究，揭示了低雷诺数下翼型气动特性恶化机理；刘强等[47]还通过数值方法对比了翼型上表面柔性蒙皮固定不动(图11(a))和以旋涡脱落频率f0振动(图11(b))时的非定常流动结构，发现2种流动结构存在很大差异，不振动时流动结构为“后缘层流分离泡”，而振动后流动结构为经典的“长层流分离泡”；刘沛清等[48]开展了吹/吸气控制翼型表面层流分离泡的数值研究，发现吹/吸气可有效抑制低雷诺数下层流分离泡的发展，明显提高低雷诺数下翼型的升阻比。

图11 单周期内蒙皮固定与振动时非定常流动结构[47]Fig.11 Unsteady flow structures for static and oscillating shin during a single period[47]

低雷诺数气动问题求解方面，目前常用的方法是雷诺平均Navier-Stokes(Reynolds Average Navier-Stokes, RANS)方程结合湍流及转捩模型的数值方法，如Langtry等[49-51]提出的γ-Reθ转捩模型，其将剪切应力输运(SST)k-ω湍流模型与经验转捩关系式结合，同时具备两方面的优点。利用这类方法可以捕捉层流分离流动的非定常、非线性效应，并获得基本气动特性，但获得的流动结构精度并不高。基于大涡模拟(Large Eddy Simulation, LES)和直接数值模拟(Direct Numerical Simulation, DNS)的精细化手段可以避免RANS方法精度不高的问题，但存在计算量大等缺点[32]。

王科雷等[52]采用求解k-kl-w湍流模型的雷诺平均Navier-Stokes方程有限体积法，对低雷诺数条件下的SD7037翼型特性进行了数值模拟，并与试验结果及S-A模型计算结果进行了对比，发现该模型能准确模拟翼型表面流动分离与再附现象(图12)。

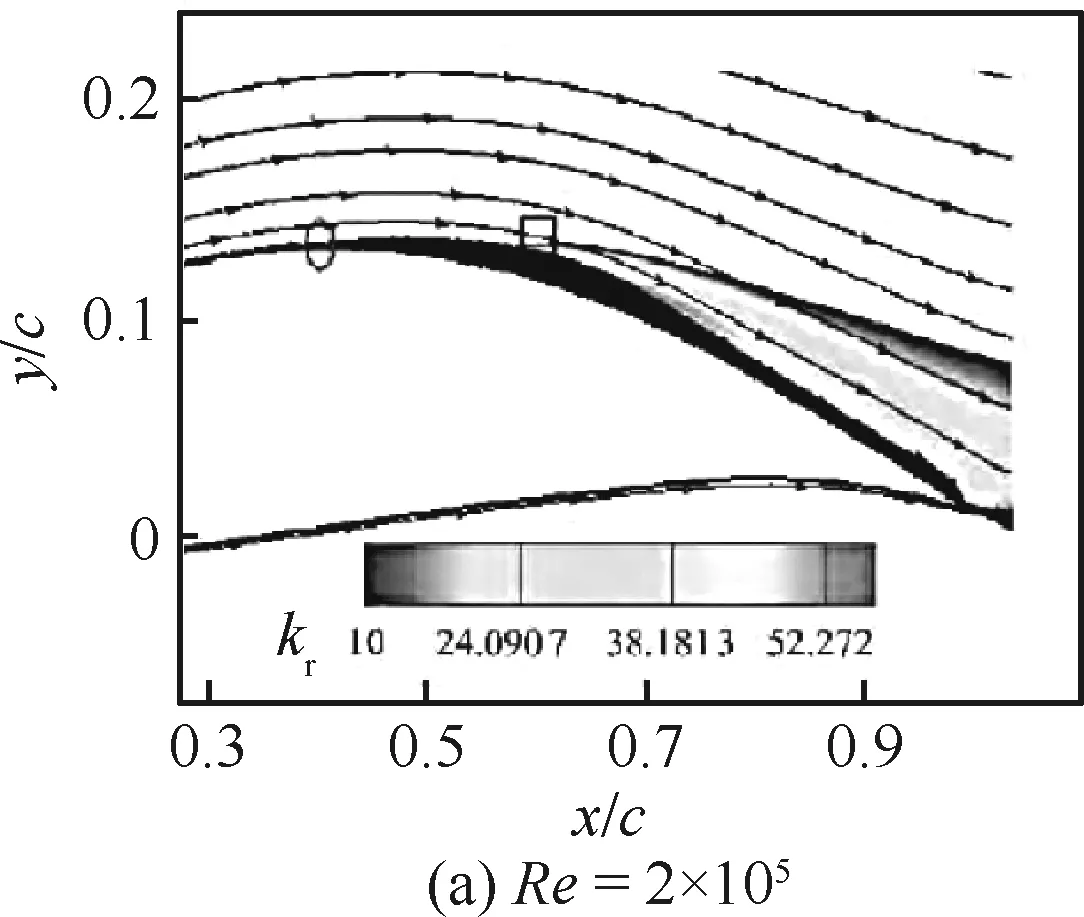
图12 6°迎角翼型流场图[52]Fig.12 Flow field diagram at 6 ° angle of attack[52]

2.2 翼型优化设计技术

超长航时太阳能无人机通常采用超大展弦比机翼，相比常规飞行器而言，诱导阻力占总阻力的比例较小，因此翼型的气动特性很大程度上决定了机翼的气动特性[53]。采用强制转捩、表面吹吸气控制等方式可以有效抑制层流分离，提升翼型气动性能，但这些方法实际应用难度较大，目前尚未普遍用于太阳能无人机。现阶段太阳能无人机机翼气动优化的主要内容仍是针对低雷诺数流动特点的翼型外形的优化设计。

太阳能无人机常用的低雷诺数翼型包括Eppler系列、SD系列等。与普通翼型相比，低雷诺数翼型在外形上的差异主要有2点：一是翼型上表面更加平坦，二是翼型厚度较小[35]。

Ma等[54]对几种典型翼型在低雷诺数下的绕流进行了数值模拟，并通过水洞试验验证了数值方法的准确性(图13)。对不同相对厚度和不同最大相对厚度的翼型绕流进行了模拟，研究结果表明，在失速特性良好的前提下，翼型最大相对厚度值应尽可能小，最大相对厚度位置应靠近后缘，这样可以获得更好的翼型性能。该研究为低雷诺数翼型优化设计提供了方向性的借鉴。

图13 4°迎角翼型上表面层流分离泡观测[54]Fig.13 Observation of laminar flow separation bubbles on upper surface of airfoil at 4° angle of attack[54]

现有的翼型优化技术主要有2种：直接设计法和反设计法[55]。由于低雷诺数条件下的气动状态难以预先给出，反设计法在低雷诺数翼型设计中的应用受到限制，直接设计法更适用于此类问题。翼型的参数化表示是优化设计的第一步，目前常用的翼型参数化描述方法有多项式拟合法、解析函数线性叠加法和曲线拟合法[56]。曲线拟合法形式简单、表达方便，其中的非均匀有理B样条曲线拟合方法是目前应用最广泛的方法。高正红等[57]采用反设计方法对自然层流翼型进行了设计，并采用非接触测量方式开展了试验验证。

国内外学者还结合太阳能电池片的特点对太阳能无人机翼型展开了研究和设计。Chen和Bernal[53]采用涡格法计算，并通过风洞试验筛选了4种利于电池片铺设的“平板”翼型(图14)，研究结果表明，相比传统大弯度翼型，“平板”翼型具有潜在的高升力和低阻力特性；刘晓春等[58]计算分析了不同雷诺数下折线型翼型的气动特性，研究了低雷诺数下折线形翼型的绕流机理，并与基准翼型进行了对比；Hobold和Agarwal[59]提出了一种翼型的光照辐射吸收模型，并针对不同飞行航线进行了独立的翼型优化，该模型对于太阳能无人机翼型综合效能优化具有重要意义。

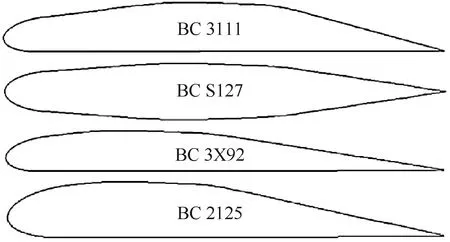
图14 4种“平板”翼型[53]Fig.14 Four "flat" airfoils[53]

文献[26]指出，若直接根据单一迎角下的升阻比进行个体评价，进而筛选出升阻比较大的翼型，该迎角下的升力系数未必满足巡航升力系数要求，即容易出现巡航升力系数与最大升阻比匹配不合理的现象。此外，如果不对升力系数加以限制，这种优化结果往往只是翼型弯度增大，迎角-升阻比曲线左右平移，而不是整体提升，如图15所示，这种优化结果可以直接通过改变安装角来实现，并不是翼型优化的理想结果。此外，如果只在一个固定升力系数处进行优化，得到的结果往往是该点的升阻比能够得到明显提高，而在偏离此升力系数时，升阻比迅速降低，如图16所示，这样的结果也不是翼型优化的理想结果。通过加权平均的方式，以多个巡航点的升阻比整体最大为优化目标，能够有效地解决升阻比曲线非增长式平移和单点最优的问题。

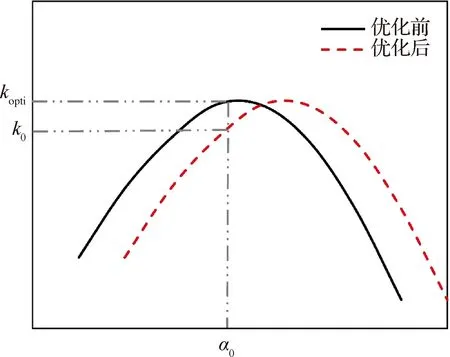
图15 升阻比曲线非增长式平移[26]Fig.15 Non-growth translation of lift-drag ratio curves[26]

图16 单点优化局部最优[26]Fig.16 Local optimum for single-point optimization[26]

2.3 气动布局设计技术

太阳能无人机发展之初最常用的气动布局有2种：常规布局(图17(a))和飞翼布局(图17(b))。

针对常规布局的理论研究已经非常完善，技术成熟而稳定，但由于常规布局飞机利用平尾产生的负升力进行纵向配平，气动效率受到限制。英国的“Zephyr”系列无人机、中国的“彩虹”无人机、俄罗斯的“Owl”无人机、意大利的“HELIPLAT”无人机等均采用了常规布局。阙建锋等[60]在常规布局的基础上，提出一种“T构型”太阳能无人机布局方案，这种布局利用巡航状态下降低重心的自配平原理，有效降低了配平损失；邓扬晨等[61]通过工程梁方法建模，探讨了常规单、双机身布局下的大展弦比直机翼的结构刚度问题，研究表明，当双机身间距为0.553 7倍机翼展长时，机翼刚度性能最佳。

飞翼布局利用反弯翼型实现机翼自配平，省去了平尾，相比常规布局而言具有更高的气动效率和更小的结构重量，但飞翼布局也具有纵向稳定性差，操控难度大的特点。美国的“Helios”无人机、“Aquila”无人机，西工大的“魅影”无人机等均采用了飞翼布局。李晨飞和姜鲁华[62]采用翼梢扭转改善飞翼无人机的稳定性，数值计算表明，机翼的几何扭转设计使得飞翼无人机零纵向力矩系数改善为正值，可在正迎角下配平，且平衡迎角处升阻比有所提高。

近年来，太阳能无人机领域出现了串列翼布局(图17(c))、分布式布局(图17(d))等新布局的尝试。

串列翼布局的前后翼面均产生升力，具有气动效率高、结构刚性好的特点。UAVOS公司推出的ApusDuo无人机即采用了前下后上式的串列翼布局，该飞机利用布局优势克服了诸多气动弹性难题，于2018年完成首飞。Scharpf和Mueller[63]对串列翼在低雷诺数下的气动特性进行了试验研究，验证了串列翼布局相比单翼布局的优势；李广佳等[64]对串列翼型在±6°翼差角的不同水平相对距离组合位置进行了数值模拟计算，结果表明，在负的翼差角下，水平位置越远，串翼系统的升阻比越高，而在正的翼差角下，水平位置越近，升阻比越高；华杰等[65]对串列翼太阳能无人机的气动特性进行了仿真和设计，并给出了前后翼最佳的相对水平距离和相对垂直距离。

相比上述几种布局而言，分布式布局更有利于太阳能无人机面对复杂气候条件和多变光照方向。美国的“Odysseus”无人机[66]采用三段式铰接机翼设计，白天，通过操纵尾翼把至少2个模块的机翼上表面倾斜到光照直射方向，使得能量收集效果比平直翼大4～5倍，这对高纬度太阳能无人机实现不间断巡航十分有利；夜晚，机翼又伸展回大展弦比平直状态，以最小的阻力形态飞行。马东立等[67]提出一种利于冬季飞行的太阳能无人机构型，其通过翼梢帆板进行机翼整体旋转，相比“Odysseus”，光照利用效率更高。德国宇航研究院DLR[68]于2017年提出了一种分布式大展弦比无人机布局方案(图18)，该布局无人机由载荷段和推进段构成，载荷段采用刚性设计，而推进段采用大柔性设计，这种布局在上升气流作用下可以实现从翼梢到另一侧翼梢的90°弯曲(图19)，提高了结构安全性，同时利用柔性段平尾操纵实现全机飞行控制。此外，该布局无人机还可根据任务要求灵活进行翼段的组合与分离，从而实现其他布局难以实现的任务目标。

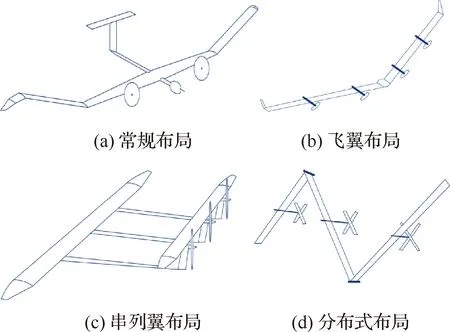
图17 太阳能无人机气动布局Fig.17 Configurations of solar-powered UAV

翼型和总体气动布局方案确定后，还需要对气动布局进行优化，主要内容包括机翼平面形状及弯扭分布的优化，以及尾翼构型的设计。减小机翼阻力的主要途径有3种：一是增大展弦比，二是增加翼梢小翼，三是通过机翼扭转改善机翼载荷分布。其中，前2种方式受限于结构强度和刚度，机翼扭转的方法应用更为普遍。于哲峰等[69]使用CATIA创建了机翼几何参数化模型，将设计参数取为各站位处的翼型和扭转角，对机翼外形进行了优化；沈琼等[70]利用几何参数化和代理模型对机翼扭转和吊舱位置同时进行了优化，代理模型的引入大大减少了优化的计算量；乔宇航等[71]基于升力线理论，提出了适用于平直机翼的几何、气动混合扭转方法，此方法的优势在于通过单次设计，即可得到具有椭圆升力分布的机翼扭转。

图18 DLR提出的可变体无人机布局[68]Fig.18 Layout of variant UAV proposed by DLR[68]

图19 风扰作用下的机翼大变形[68]Fig.19 Large deformation of wing under wind disturbance[68]

3 气动弹性与阵风减缓技术

超长航时太阳能无人机的大展弦比机翼在载荷作用下，会产生很大的弯曲和扭转变形，带来了诸多气动弹性方面的问题，影响着飞机的操控性能和飞行安全。

首先，在动力学建模方面，刚性飞行器假设已不适用于该类飞机，不能再进行简单的刚体假设。国内外目前对大展弦比柔性飞行器的动力学建模方式主要有2种[72]：一是基于机理的建模方法，即通过分析确定飞行器的受力与运动关系构建其飞行动力学模型[73-74]；二是基于系统辨识的建模方法，即将飞行器视为“黑箱”，通过给定输入得到输出，进而得到输入输出的一般关系[75-76]。

其次，在发散、颤振边界预测方面，基于小变形假设的气动弹性分析手段已不适用于这类大展弦比飞行器，分析时必须考虑结构的几何非线性效应。结构几何非线性对大展弦比飞机的影响体现在2个方面：一是结构整体刚度依赖不同的载荷状态而改变；二是机翼平面形状的改变影响到气动力的分布[77]。Dunn和Dugundji[78]较早进行了大展弦比复合材料机翼非线性气动弹性稳定性的理论和试验研究；随后，Cesnik等[79]基于Hodges几何精确非线性一维梁模型、VABS复合材料梁截面分析法和Peters入流气动力模型，建立了低阶高精度的大展弦比复合材料柔性机翼非线性气动弹性分析模型；谢长川等[80]建立了大变形弯曲机翼的定常气动计算方法，并结合结构几何非线性有限元方法，建立了大柔性机翼静态气动弹性和颤振的系统分析方法；安效民和徐敏[81]基于Co-rotational理论，发展了一种几何大变形下的非线性气动弹性求解方法。

最后，阵风减缓方面，大展弦比太阳能无人机在起降过程中需要穿越对流层，会受到强烈的阵风影响，造成较大附加过载，对飞行安全带来威胁。研究表明[82-83]，阵风的大小与湍流强度直接相关，湍流越强，阵风系数越大。由于越靠近地面，湍流交换越剧烈，因此地面的阵风系数最大，随着高度增加，风场逐渐变得稳定，文献[84]提出的阵风模型表明，阵风系数随高度变化基本呈现负指数变化；此外，海拔高度越低，太阳能无人机的巡航速度越低，阵风对飞机的气动干扰越明显。综合以上两点，太阳能无人机起降阶段最易受到湍流效应和阵风干扰产生安全问题。通过气象预测，选择风速小，湍流强度弱的天气作为起降窗口期，可以大幅降低湍流引发的事故率，然而，采取气象保障措施不能完全确保起降阶段不会遭遇湍流，太阳能无人机遭遇湍流而坠毁的事件仍频繁发生。“Helios”无人机在2003年6月飞行时遭遇强湍流，致使整个机翼诱发严重的俯仰振荡，超出了结构的扭曲极限，发生解体；“Zephyr”无人机于2019年9月在澳大利亚试飞时遭遇湍流，飞机脱离了受控飞行而发生坠毁。常规刚性飞机通常采用抗侧风控制算法抑制湍流影响，方法主要有3种：侧航法、侧滑法和直接力法[85]，而太阳能无人机柔性大，响应慢，这3种方法并不是抵抗湍流和阵风的最佳策略。目前，国内外关于太阳能无人机抑制湍流影响的研究主要集中在阵风减缓方面，阵风减缓控制可以有效降低湍流对太阳能无人机的干扰效应，进一步降低事故发生率[86-87]。

国内外学者提出的阵风减缓措施主要有2种：被动控制和主动控制。其中，被动控制主要依靠新材料、优化机翼结构参数等方法来提高机翼刚度，该方法对机翼高频振动抑制有较好作用，但对低频振动的抑制效果较差。主动控制主要通过在机翼上加装作动器，改变气动外形，进而抑制颤振。自20世纪60年代起，美国就利用B-52、C-5A等飞机作为验证机，进行了各种主动控制技术的验证[88-89]，而后学者开始将阵风减缓技术应用到大展弦比柔性飞行器中。Botez等[90]使用线性二次高斯(LQG)控制技术进行阵风减缓，将扰动下的垂直方向加速度降低了99%(图20)；Dillsaver等[91]以一架超大展弦比柔性飞机为研究对象，基于耦合刚体的非线性模型和柔性飞机的弹性模态，设计了一种阵风减缓控制系统，该系统可以将线性模型的峰值机翼曲率降低56%；Wang等[92]利用静态输出反馈对柔性太阳能无人机进行阵风减缓，使其翼尖偏转减小33%；Miller[93]提出一种用于阵风减缓的翼梢装置(图21)，该装置通过控制翼梢后方的水平操纵面来改善机翼的载荷特性，美国“太阳鹰”无人机即采用了此种设计。

图20 阵风减缓动态响应[90]Fig.20 Gust mitigation dynamic response[90]

4 飞行控制技术

超长航时太阳能无人机翼载荷通常比常规无人机低1～2个数量级，质量特性和气动特性相比常规无人机都有着明显区别。较低的飞行速度使得太阳能无人机的空速处在与风速相同的量级，风速相对空速不再是小量。稳定的风场会影响飞行轨迹控制，而变化风场会对飞行造成扰动，增加控制难度，因此需要重点关注太阳能无人机的控制技术[32]。

稳定性方面，超高空超长航时太阳能无人机气动导数与常规低速飞行器存在差异，尤其是横航向气动导数差异较大，文献[94-95]对此进行了详细分析。研究表明，临近空间太阳能无人机滚转交感导数较大，偏航阻尼导数较小，导致其螺旋模态容易发散；航向气动阻尼力矩与惯性力矩比值较大，导致荷兰滚模态阻尼比较大。稳定风场不会影响横航向模态特征根，但会使横航向特征矢量发生改变。纵向稳定性方面，临近空间太阳能无人机无量纲俯仰转动惯量与俯仰阻尼导数比值较小，导致动阻尼力矩影响大，因此短周期模态阻尼比较大；而由于空气密度低，气动力阻尼小，导致其长周期模态阻尼比相比常规飞行器大。

图21 翼梢阵风减缓装置[93]Fig.21 Wingtip gust mitigation device[93]

横航向控制策略方面，太阳能无人机的大展弦比机翼通常为柔性轻质结构，扭转刚度低，若采用副翼控制滚转的方式，容易造成副翼效率下降甚至反效，因此“Zephyr”“Helios”等诸多太阳能无人机都取消了副翼，此外，“Skylark”“RQ-11”等小型无人机为降低系统复杂程度也取消了副翼。目前，太阳能无人机的横航向控制主要有2种途径:一是利用方向舵进行航向控制，二是利用多个螺旋桨的差动实现航向控制。

偏转方向舵可以使机头偏转产生侧滑角，在横向静稳定力矩的作用下飞机产生倾斜角，实现转弯，“Zephyr”系列无人机即采用这种方式。与副翼直接产生滚转力矩不同，方向舵控制先产生侧滑，再依靠横航向稳定性产生滚转力矩，因此需要匹配无人机的操纵性与稳定性,这种转弯方式要求飞机横航向具有良好的匹配性。Meola等[96]基于PID控制理论设计了由偏航阻尼、滚转角控制和偏航角控制组成的横航向控制器，结果表明采用方向舵控制滚转是可行的；Knot等[97-100]重点研究了利用机翼主动变形产生的滚转力矩进行横航向控制的方法；成鑫等[101]通过仿真及实验分析了无副翼电动无人机的飞行品质，对比了上反角与尾容量对横航向操稳特性的影响。

多个螺旋桨产生的偏航力矩具有可叠加性，而其他方向的附加耦合力矩很小，因而可以利用螺旋桨差动进行航向操纵，“Helios”系列无人机即采用该种方式。目前针对螺旋桨差动控制的研究主要集中在控制分配与操稳特性分析方面。赵维娜等[102]提出了基于能量约束的太阳能无人机多螺旋桨差动控制分配方法；徐明兴等[103]以提高动态过程中的螺旋桨效率为设计目标，通过伪逆法分配各个螺旋桨推力并设计了动态增益补偿，用来削弱因螺旋桨动态特性带来的不利影响，提出了以误差和螺旋桨拉力二范数最小为目标的螺旋桨差动控制分配方法；肖伟等[104]建立了分布式推进系统的数学模型，研究了分布式推进系统分布位置和控制方式等对太阳能无人机横航向飞行品质的影响；王睿等[105]指出螺旋桨产生的附加偏航阻尼可以改善荷兰滚和螺旋模态的稳定性，并以螺旋桨的转速变化量最小为优化目标，研究了最优航向控制分配方法。

螺旋桨差动所需功率随提供的偏航力矩系数近似呈二次方关系，如图22所示，当所需偏航力矩较大时，采用螺旋桨差动方式进行操纵会造成额外的能量损失，若将螺旋桨差动控制与方向舵偏转控制耦合，可有效提高操纵效率。文献[26]对这种联合控制方式展开研究，研究结果表明，提供相同偏航力矩时，方向舵偏转引起的功率增量小于螺旋桨差动(图23)，而当同时采用2种控制方式时，所需消耗的额外功率小于单独一种方式。保持航线飞行时，适合单独采用方向舵操纵，而进行大范围航向调整时，适合采用联合操纵方式。

图22 功率增量随提供的偏航力矩系数的变化[26]Fig.22 Variation of power increment with yaw moment coefficient provided[26]

5 高效能源技术

如图24所示，太阳能无人机通过能源、动力两大系统将光能转化为机械能，期间各环节均造成了能量损失。其中能源系统由太阳能电池、储能电池和能源管理系统3个子系统构成，每个子系统相对独立又相互制约，其技术水平直接决定了无人机方案的可行性[106-108]。

图23 功率增量随偏航力矩系数增量的变化[26]Fig.23 Variation of power increment with increment of yaw moment coefficient[26]

5.1 太阳能电池技术

太阳能电池种类繁多，不同电池的光电转换效率和物理特性均有差别[109-110]。太阳能无人机一方面对电池效率有较高要求，另一方面也要求电池具有良好的物理特性，包括低面密度、易附形、耐高/低温、耐辐射和耐腐蚀等[109, 111-112]，因此只有少量种类的太阳能电池被应用于太阳能无人机，主要包括硅电池和薄膜电池。

硅电池包括多晶硅电池、单晶硅电池和非晶硅电池等[113]。单晶硅电池是硅电池中效率最高的，实验室效率可达25%，货架产品效率在16%～22%之间，该类电池曾广泛应用于多个型号的太阳能无人机，如“Zephyr-6”“Helios”(图25(a))[114]等，但其比功率较低，且刚性较大，不利于维持机翼表面的光滑性；非晶硅电池相比单晶硅电池效率较低，但比功率更高，当用于铺片的机翼面积较宽裕时，非晶硅电池在提供与单晶硅电池相同功率的情况下，付出的重量代价更低。

图24 太阳能无人机能源和动力系统Fig.24 Energy and power system of solar powered unmanned aerial vehicle

图25 太阳能无人机铺设太阳能电池片Fig.25 Solar cell paving for solar powered UAV

薄膜电池单体厚度薄，质量面密度低，且附形能力强，满足柔性大展弦比机翼的铺片需求。薄膜电池常见的基底材料包括GaAs[115]、CdTe[116]、Cu(InGa)Se2[117]、TiO2[118]、CIS(CIGS)[119]等。其中，GaAs薄膜电池效率最高，多结GaAs电池实验室效率已达到40%以上[120]，由于成本较贵，最初多用于卫星等航天器，在太阳能无人机上的应用尚不普遍。近年来，随着制备工艺的完善和成本的降低，GaAs开始更多地应用到太阳能无人机中，“Zephyr”系列最新的“Zephyr-S”无人机(图25(b))[121]即搭载了GaAs电池。

美国国家可再生能源实验室(NREL)追踪记录了太阳能电池的最新研究进展[122]，如图26所示。近十年来，薄膜电池成为太阳能电池研究的重点，GaAs电池效率持续提高，其中最新的四结GaAs电池效率达到了47.1%；硅电池中，单晶硅电池效率提升幅度较小，目前最新产品的效率可达27.6%，而本征薄层异质结(HIT)硅电池效率近年来提升较快，性能有超越单晶硅电池的趋势。

目前，太阳能电池效率已基本满足太阳能无人机功率需求，从目前成功试飞的多架太阳能无人机的电池布置情况来看，铺片率并未取极限数值，在这种情况下，质量比功率参数就显得更为重要，更轻更薄的太阳能电池将成为未来太阳能无人机应用的主流。

图26 太阳能电池单体效率[122]Fig.26 Solar cell monomer efficiencies[122]

5.2 储能电池技术

储能电池重量一般占太阳能无人机全机重量的30%以上，是影响方案成败的重要因素之一。历史上，太阳能无人机上采用的储能电池先后有银锌电池(Ag-Zn)、镉镍电池(Ni-Cd)、氢镍(Ni-MH)电池、锂离子电池(Li-ion)、锂硫电池(Li-S)和燃料电池等[108]。常见储能电池特性[123]如表2所示，锂离子电池和锂聚合物电池在太阳能无人机领域应用最为广泛[124]。其中，锂离子电池的优势在于比能量高，工作电压高(3.6 V以上)，循环使用寿命长，自放电小，且负极材料具有多元性的特点。“Sunrise”和“Sky Sailor”无人机搭载的锂离子电池能量密度分别为145 W·h/kg和170 W·h/kg。锂聚合物电池能量密度略大于锂离子电池，且成型工艺更好，“Solong”无人机和“Solar Impulse”载人飞机分别搭载了5.6 kg和400 kg锂聚合物电池，能量密度在180～240 W·h/kg之间。但对超长航时太阳能无人机来说，这样的能量密度仍无法满足不间断巡航的要求，装备这些电池的太阳能无人机都未实现高空跨昼夜飞行。《中国制造2025》中确定的目标是，中国生产锂离子电池的能量密度2020年达到300 W·h/kg，2025年达到400 W·h/kg，2030年达到500 W·h/kg。可见，锂离子电池未来仍有广泛应用于超长航时太阳能无人机的前景[125]。

锂硫电池的理论能量密度高达2 600 W·h/kg[126-127]，是锂离子电池的3～5倍，“Zephyr7”无人机搭载了Sion Power公司生产的锂硫电池，其能量密度为350 W·h/kg，这些电池被分布式安装在机翼内部，用于减小翼根弯矩和机翼变形。文献[128]对锂硫电池进行了详细介绍，此类电池优势明显，但缺点也不容忽视，聚硫化物在电解质中的溶解问题、硫正极锂化后体积膨胀、锂负极枝晶问题等，导致了其较差的安全性和循环性能[129]，因此锂硫电池在太阳能无人机储能电池体系中并不占主导地位。

可再生燃料电池是另一类能量密度较高的储能电池，被广泛应用于各类无人机[130]。其中，应用最广泛的氢氧燃料电池效率可达65%～85%，能量密度500～700 W·h/kg[131]。“Helios”无人机在方案确立阶段锂电池技术尚不成熟，只有燃料电池可满足其400 W·h/kg的指标需求，因此其最终搭载了120 kWh氢氧燃料电池(图27)作为储能设备[132]。目前，碳纤维复合材料高压储氢方式可将质量储氢密度提高到10%[133]，有机液体氢化物储氢方式的质量储氢密度约为6.5%～7.5%，金属氢化物储氢方式的质量储氢密度仅为1.5%～3%[134]。但综合来看，任何一种储氢方式均会带来数倍于氢气的额外重量，从而降低燃料电池的能量密度，这在技术层面是无法避免的。刘莉等[135]综合考虑太阳能电池和氢氧燃料储能电池的特性，提出了一种考虑全机重量能量耦合关系的总体设计方法和任务剖面驱动的能源管理策略，并进行了各种能源特性的仿真分析。

如图28[106]所示，燃料电池与锂离子/锂聚合物电池相比，能量密度较大，功率密度较低，但这两类电池的能量密度和功率密度均高于其他类型电池，因此一段时间内仍将是太阳能无人机储能电池体系中的主流。

表2 常用储能电池特性[123]Table 2 Characteristics of common energy storage batteries[123]

图27 “Helios”搭载的氢氧燃料电池[132]Fig.27 Hydrogen and oxygen fuel cells on “Helios”[132]

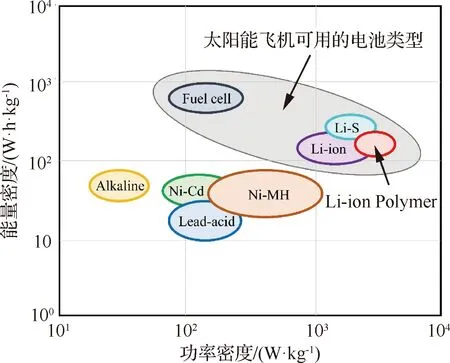
图28 储能电池性能分布[106]Fig.28 Performance distribution of energy storage batteries[106]

5.3 能源管理技术

超长航时太阳能无人机的功率输入值与输出值始终处于变化状态，需要能源管理系统根据太阳能电池功率和系统负载的变化对电能进行实时管理和分配，避免不合理的消耗。能源管理系统的关键在于最大功率点跟踪(Maximum Power Point Tracking，MPPT)技术，通过对太阳能电池和储能电池的电流和电压进行监视，根据优化算法实时改变DC/DC转换器的增益，使得太阳能电池始终工作在功率最大点，再通过配电器进行功率分配[136-138]。

李钏等[139]对MPPT技术发展现状进行了综述，详细介绍了MPPT系统的拓扑结构、跟踪太阳能电池阵最大功率点的工作过程、软件和硬件电路的设计与实现，其中，已转化为工程应用的3种MPPT拓扑结构技术指标如表3所示。

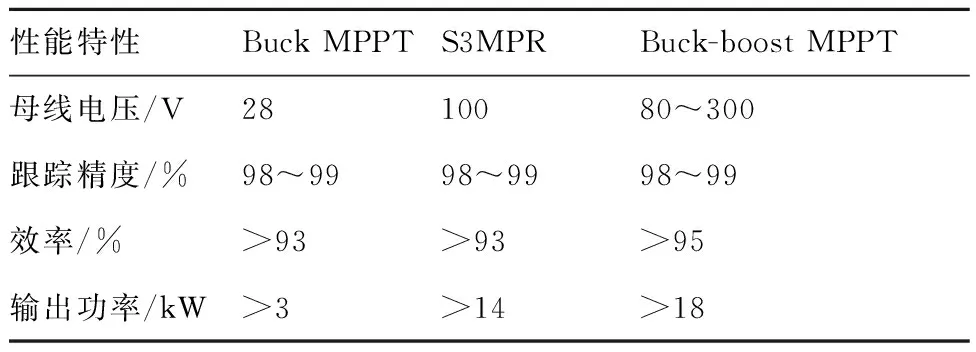
表3 3种拓扑结构的MPPT性能对比[139]

6 动力推进技术

高空长航时太阳能无人机动力推进系统由电机和螺旋桨构成，需要具备质量轻、效率高的特点，并且要求在高空低密度空气中运行可靠，控制稳定。此外，推进系统还与气动、结构、控制等方面具有耦合效应，是太阳能飞行器研究的重点内容。

6.1 电机技术

传统有刷电机的电弧磨损速度较快，不适用于长航时飞行，而永磁无刷电机效率高，重量轻，磨损速度慢，成为太阳能无人机的首选电机类型。“Helios”无人机即采用14台均布在机翼上的永磁无刷直流电机带动螺旋桨提供飞行动力[140]，其中每台电机额定功率为1.5 kW，质量为5 kg，转速范围为200～1 500 r/min；“Zephyr”无人机也采用了永磁无刷直流电机[141-143](图29(a))，其采用表贴式外转子集中绕组结构形式，减小了磁轭厚度和端部绕组长度，优化了极弧系数，实现了高效和轻量化设计，其中每台电机额定转速为1 300 r/min，额定转矩为1.9 N·m，轻载时电机本体最高效率为93.8%。“HELIPLAT”无人机采用了轴向磁通盘式永磁同步电机(图29(b))，电机质量为4.38 kg，轻载时电机效率可达96.1%。

图29 太阳能无人机电机[143]Fig.29 Motors of solar powered UAV[143]

太阳能无人机采用的电机驱动方式有“减驱”和“直驱”2种，“减驱”方案在电机和螺旋桨之间加装了减速齿轮机构，整体优化了动力系统的匹配效能，但减速齿轮带来的机械效率损失与可靠性问题制约了“减驱”方案的进一步发展[144]，例如“Zephyr”无人机就曾因齿轮箱故障而导致飞行失败[145]，因此“直驱”仍然是目前高空太阳能无人机电机系统发展的主流。

临近空间稀薄的空气、复杂的环境，对电机的散热和性能均有影响，中国学者针对临近空间对电机的特殊要求展开了大量研究。张成明和李立毅[144]分析阐释了临近空间复杂工况环境对电机装置提出的性能指标要求，分析研究了极槽配合、损耗分配比例、磁极形式、槽型结构对电机性能的影响规律；王真等[146]将电机和减速器进行了一体化设计，降低了整体重量，并针对临近空间工作环境，对高功率密度电机组件进行了热仿真；吴洋和郭军[147]基于有限元方法，模拟了翅片散热器在临近空间工作时的工况，得到了翅片的温度场分布、热梯度、热流密度等热力学结果。

从国外临近空间飞行器推进系统发展现状来看，方波无刷直流电机和正弦波永磁同步电机是目前的主流电机类型[148-149]，而未来可能满足超长航时太阳能无人机需求的电机类型有2种：双转子电机及超导电机[150-152]。

6.2 螺旋桨技术

超长航时太阳能无人机采用的螺旋桨有定距和变距2种[153]。定距桨可在特定速度区间内发挥最大效率，构造简单，重量轻；变距桨可以通过机构改变桨距，但操纵机构复杂，会带来额外的重量及可靠性问题。目前大多数太阳能无人机采用的是定距桨，也有无人机采用了变距桨，如“秃鹰”无人机等。

高空空气密度低，导致螺旋桨翼型绕流雷诺数较低，但马赫数较高，因此应采用低雷诺数高亚声速高升力翼型。杜绵银等[153]对临近空间低速飞行器螺旋桨技术难点进行了分析，认为保持前缘层流流态、抑制分离泡产生和推迟分离是该类螺旋桨翼型的设计重点；马蓉等[154]针对临近空间螺旋桨低雷诺数翼型展开研究，同时通过对比3种典型的低雷诺数高升力翼型(LNV109A、E387/E423、S1223)，指出在翼型压力分布峰值之后保持适当的逆压梯度是高亚声速低雷诺数翼型设计的重要准则。

国外开展了大量低雷诺数螺旋桨设计研究，这些螺旋桨的高空巡航阶段效率普遍在80%以上。美国“Helios”采用的两叶定距桨具有宽弦分布规律，在巡航高度27 km，前进比为0.83时，效率可达80%；德国宇航研究院DLR在20 km高空开展了临近空间螺旋桨试验，所测试的螺旋桨在前进比为2.0时，效率可达84%；日本航宇开发局JAXA进行了平流层飞艇与动力系统一体化设计研究，设计得到的螺旋桨效率达80%。

此外，高空太阳能无人机通常采用沿翼展分布的多螺旋桨推进系统，螺旋桨通常位于机翼前缘之前，两者均处于低雷诺数范畴，而翼型表面的层流和分离现象对扰动较为敏感，因此两者之间的干扰效应不可忽视[148]。一方面，螺旋桨的滑流区域占机翼面积的比重较大，且流场复杂，对机翼气动性能产生的影响十分明显(图30)；另一方面，这种耦合效应是相互的，螺旋桨的特性也会受机翼影响而产生变化。

图30 螺旋桨对机翼的干扰作用[148]Fig.30 Interference of propeller on wing[148]

目前国内外发展了多种用于模拟相互干扰的工程估算方法，如李博等[155]建立了考虑桨叶形状、桨叶角、三维效应等因素的等效盘模型，并利用其代替真实螺旋桨研究了滑流对全机气动力的影响；鄂秦等[156]分别对螺旋桨和全机划分涡元，实现了螺旋桨涡系与全机涡系的干扰模拟；然而为了更准确地分析干扰的复杂机理和气动特性，必须采用非定常方法模拟螺旋桨与机翼之间的相对运动，Bousquet和Gardarein[157]基于非定常Euler方程和滑移网格技术，模拟了螺旋桨飞机的绕流；Schwarzer等[158]基于嵌套网格技术，模拟了螺旋桨的滑流运动，并对Euler方程和Navier-Stokes方程的计算结果进行了对比；乔宇航等[159]采用滑移网格求解方法(图31)，对螺旋桨/机翼相互干扰进行了非定常数值模拟，并与干净螺旋桨和干净翼段的气动特性进行了对比(图32)。与工程估算方法相比，非定常模拟方法可以更准确地分析螺旋桨与机翼干扰的复杂流场结构，以及滑流对螺旋桨/机翼的影响[160]；此外，通过求解描述黏性流动的Navier-Stokes方程可以更真实地模拟干扰的影响[161]。

图31 螺旋桨/机翼网格[159]Fig.31 Propeller/wing mesh[159]

图32 流场空间湍动能分布[159]Fig.32 Distribution of turbulent kinetic energy in flow field[159]

7 飞行轨迹优化技术

能源动力系统发展水平是影响超长航时太阳能无人机发展的重要因素，但这些关键技术的进步需要消耗大量的人力和物力，研发过程中时间成本的消耗也很大程度上制约了无人机技术的革新。飞行轨迹优化为提升超长航时太阳能无人机的任务可行性提供了又一重要途径，这是区别于常规无人机的重要研究内容[162]。

7.1 飞行轨迹优化措施

目前，太阳能无人机轨迹优化主要有2种措施。其一是飞行高度保持不变，通过飞行姿态的变化，使太阳能电池吸收的能量更多。这种优化方式主要利用太阳光入射角与无人机姿态角的耦合作用。Klesh和Kabamba[163-164]假设飞行高度、太阳高度角和方位角保持不变，以飞行速度和倾斜角为变量，以剩余能量最大为目标，给出了水平面内点到点飞行任务最优飞行轨迹的解析解,其研究结果表明：在太阳高度角较小时，以远航速度无倾斜飞行可以实现轨迹最优；在太阳高度角较大时，以久航速度倾斜飞行能够获得更多的能量。Spangelo等[165-166]将飞行轨迹用周期性样条函数表示，采用太阳高度角、空气密度不变的假设，引入加速度波动值来修正目标函数以改善轨迹不光滑问题，研究了短时间小半径盘旋时的最优轨迹。其研究指出，采用变姿态变速度的优化轨迹能够获取更多的能量，随太阳高度角减小，效果更显著，而当太阳高度角过小(<15°)时，通过该轨迹无法获得更多能量。此外，椭圆轨迹相比于圆形轨迹具有更大的能量优势。Ma等[167]推导了最优水平转弯过程的必要条件，进一步得到了转弯过程中的最优滚转角控制律。其研究指出，只有当功率小于初始速度对应的平飞需用功率时，才能完成最优转弯。Ran[168]考虑了天气因素，结合图谱法和Bellman-Ford搜索算法，研究了低空水平飞行的轨迹规划问题。在此基础上，学者针对地面目标追踪、多机联合监视等特殊任务开展了轨迹优化[169-173]，在这些研究中，无人机的运动限定在二维水平面内。

其二是改变飞行高度，利用重力储能代替部分储能电池的作用[174]。Gao等[175]以单位高度差内滑翔时间最长为优化目标，采用Gauss伪谱法研究了下滑过程的最优轨迹。其研究表明：增大设计升力系数的范围有利于获得更长的留空时间，飞行高度越低，单位高度差内滑翔时间更长。通过引入航时因子，分析了重力储能和二次电池的等价性[176-177]，但在对比时能量环节效率的统一性和等强度辐照假设的合理性需要进一步探讨。在以上研究基础上，Gao等[178-179]提出了一种“平飞—爬升—下降”的昼夜闭环能量管理策略。此外，高显忠[177]还对风梯度获取能量的运动特征进行了分析，提出基于特征描述的飞行器风梯度飞行轨迹生成方法(图33)。

图33 典型风梯度飞行航迹[177]Fig.33 Typical wind gradient flight track[177]

王少奇等[162]同时采用改变飞行姿态和飞行高度的方式，建立了太阳能无人机三维轨迹优化模型。采用Gauss伪谱法在一系列离散点上近似状态变量和控制变量，且在配点上满足动力学微分方程的约束，将最优控制问题转化为非线性规划问题。针对一种典型的点到点飞行任务，以储能电池最终电量为目标函数，开展了飞行轨迹优化，并与定高定速飞行轨迹进行了对比(图34[26]、图35[26])。

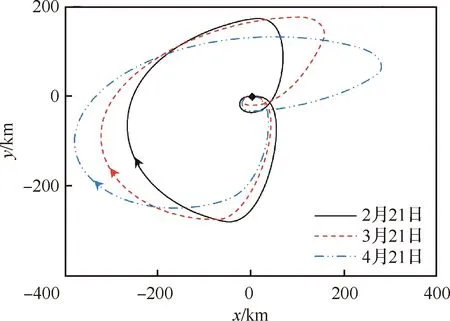
图34 不同日期的能量最优轨迹在x-y平面的投影[26]Fig.34 Projection of energy optimal trajectories on different dates on x-y plane[26]

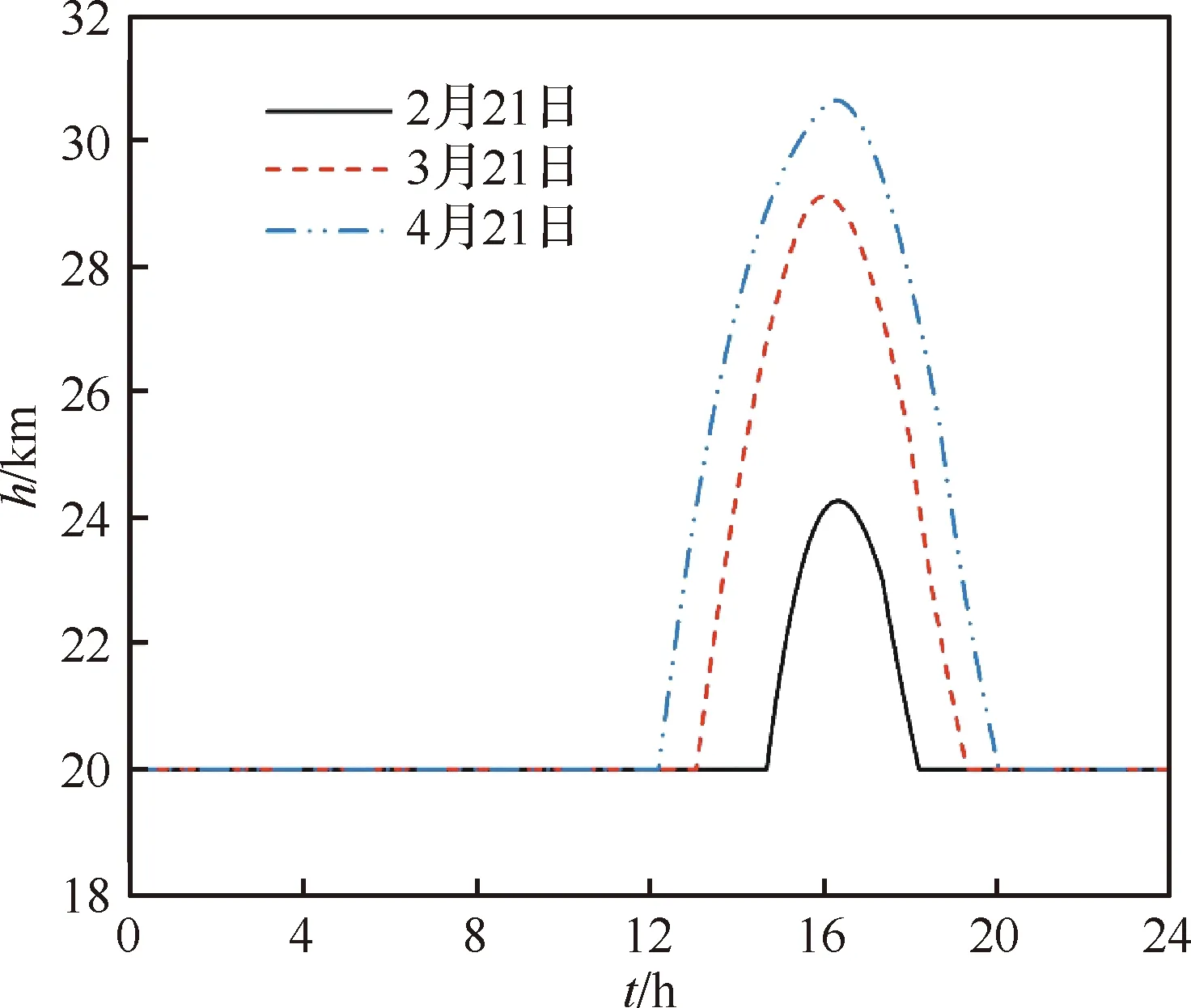
图35 不同日期能量最优轨迹的飞行高度[26]Fig.35 Flight height of optimal energy trajectories on different dates[26]

7.2 飞行轨迹优化问题求解方法

目前，求解轨迹优化问题的方法可以分为2大类：间接法和直接法[180]。间接法不对性能指标函数直接寻优，而是基于Pontryagin极大值原理，通过推导最优控制问题的一阶必要条件，将其转化为Hamiltonian边值问题。间接法求解精度高，且最优解满足一阶最优性必要条件，但对于复杂非线性问题，间接法的推导过程比较繁琐复杂。当求解两点边值问题时，收敛域很小，对初值依赖性高，部分协调变量无直接物理意义，初值选取难度大；当存在过程约束时，间接法难以实施。

直接法通过将连续的问题离散化、参数化，采用数值方法直接寻优。近年来，随着计算机技术的发展，直接法得到较快发展并广泛应用于飞行轨迹优化问题。直接法可分为2种：只离散控制变量与同时离散控制变量和状态变量。前者容易收敛到局部最优解，后者通过将状态变量的导数和运动方程右函数相匹配，能在一定程度上改善该问题。

伪谱法是一种同时离散控制变量和状态变量的直接法[181-182]。该方法通过采用全局插值多项式的有限基在一系列离散点上近似状态变量，采用多项式的导数来近似状态方程中状态变量的导数，且在一系列配点上满足动力学微分方程的约束，将微分方程的约束转化为代数约束。伪谱法因其具有参数少、精度高的特点备受关注[183]。

常用的伪谱法有Gauss伪谱法、Radau伪谱法以及Legendre伪谱法。这些方法的区别在于配点的选择不同。就计算效率而言，对于相同规模的问题，这3种方法差别不大。Gauss伪谱法和Radau伪谱法在对变量的近似精度上比Legendre伪谱法有一定优势。同时，Gauss伪谱法在边界条件的近似精度上要显著高于Radau伪谱法，适用于处理包含终端条件的问题。

8 总结与展望

本文对超长航时太阳能无人机涉及的关键技术研究现状进行了综述，并对各项技术的难点和发展方向进行了阐释。太阳能无人机的设计需要从系统最优的角度出发，结合气动、结构、控制、能源等多项技术开展多学科优化设计，基于目前各子系统技术近、中、远期可达的发展水平确定设计参数。Rajendran和Smith[3]根据各项技术的发展趋势，预测了未来20年太阳能无人机的发展情况(图36)。其认为，气动、结构虽然是影响飞行器平台性能指标的重要因素，但发展空间有限，太阳能电池、储能电池效率和能量密度的提升，将是影响未来太阳能飞行器性能的关键。研究表明，2032年左右，太阳能无人机载荷重量与结构重量的比值将达到常规电动无人机水平，2040年左右，搭载固定重量载荷的太阳能无人机最大起飞重量将下降到目前的1/3。未来，超长航时太阳能无人机将具有更为完备的任务体系和更加完善的功能，气动-结构-隐身一体化设计技术、变体布局综合设计技术、健康监测与故障处理技术等也将成为超长航时太阳能无人机设计的关键。