多复杂系数滤波器在风电并网变流器中的应用

（国网浙江省电力有限公司宁波供电公司，浙江 宁波 315000）

0 引言

风能作为一种清洁无污染且具有大规模开发利用前景的可再生能源发展迅速，但为了满足零电压穿越能力[1-2]的苛刻要求，需要风力发电系统能快速准确地检测出电网电压相位、幅值大小以及频率的波动。

以往电网电压同步信号大多采用过零点检测，但过零检测每个周期才能得到2 次电网信号信息，追踪速度很低，且受电网电压波动、背景噪声、信号零值点和频率波动影响大，导致同步信号检测误差很大。文献[3]指出基于瞬时无功功率的p-q 法只适用于电网电压对称且无畸变情况下的检测。文献[4]提出的基于FFT（快速傅里叶变换）的检测方法延迟时间长，实时性差。文献[5]提出了用小波变换原理提取基波分量的方法，但由于很难构造出符合条件的小波，其检测精度有待提高[6]。文献[7]提出的以自适应噪声对消技术为原理的自适应电流检测法虽然对元件参数的依赖性不大，但不能滤除基波负序分量且动态响应速度慢[8]。文献[9]提出的ip-iq检测法，虽然有较好的实时性且计算量小，但当电网电压不对称时，该方法的精度不高。文献[10-11]提出的瞬时对称分量法、文献[12]提出的基于瞬时对称分量法的延时信号对消法和文献[13-14]提出的空间矢量滤波法在电网频率恒定的情况下取得了较好效果，但当电网频率变动时，检测同步信号效果差。

本文提出一种新的基于MCCF（多复杂系数滤波器）的同步技术，在畸变和不平衡电网电压下，不需要对称分量算法或复杂的旋转坐标变换条件，能够精确、快速估算得到基波正序、负序分量和其他谐波分量。

1 多复杂系数滤波器

1.1 复杂系数滤波器

为了从电网电压中提取基波分量而不受其他电压谐波干扰，可以选用BPF（带通滤波器）。然而这些传统的滤波器只有频率选择特性，却不具有极性选择特性，也就是说不能区分同一频率下的正负极性。图1 为一个阻尼比ξ=0.707 的典型实系数二阶BPF 的伯德图。

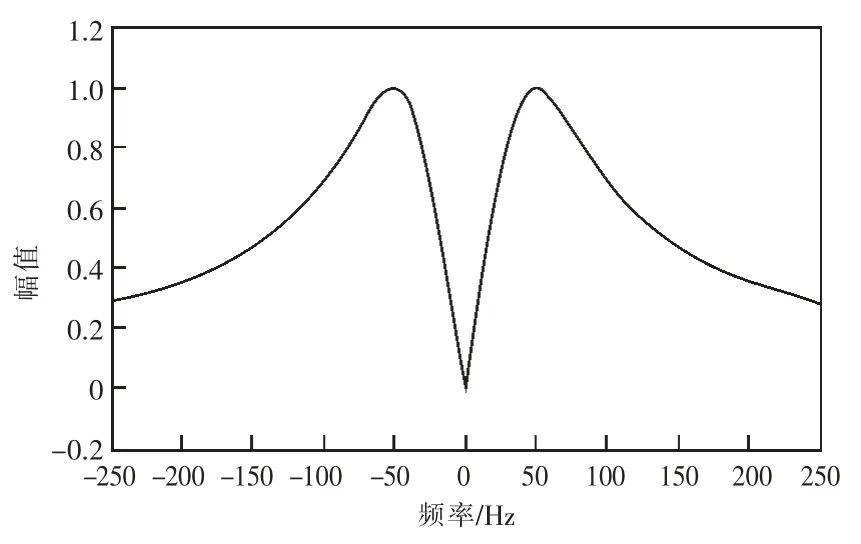
图1 二阶BPF 的伯德图

从图1 可以看出，基波正序和基波负序的衰减比都是1，也就是说基波正序和基波负序都可以完全通过BFP 而不衰减。但是，正、负序分量不能直接被滤波器提取出。相比而言，CCF（复杂系数滤波器）同时具有频率选择特性和极性选择特性。实际上，CCF 已广泛应用于工业领域，但在风电网侧变换器中被用于实时提取正、负极性还没有受到太多关注。

一个理想的CCF 不但应对所需频率保持单位增益和零相移，对其他频率有大的衰减，还要对实时信号提取提供快速响应。一种典型的一阶CCF 可用式（1）表示，其响应的伯德图见图2。

式中：ωc为截止频率；ω0为待提取的特定频率分量。ωc和ω0设为314 rad/s（定义）。

由式（1）可知，滤波器能够提取特定的频率ω0分量，并保证单位增益和零位移。同时其他频率的幅值衰减比为，相移为arctan[（ω0-ω）/ωc]。

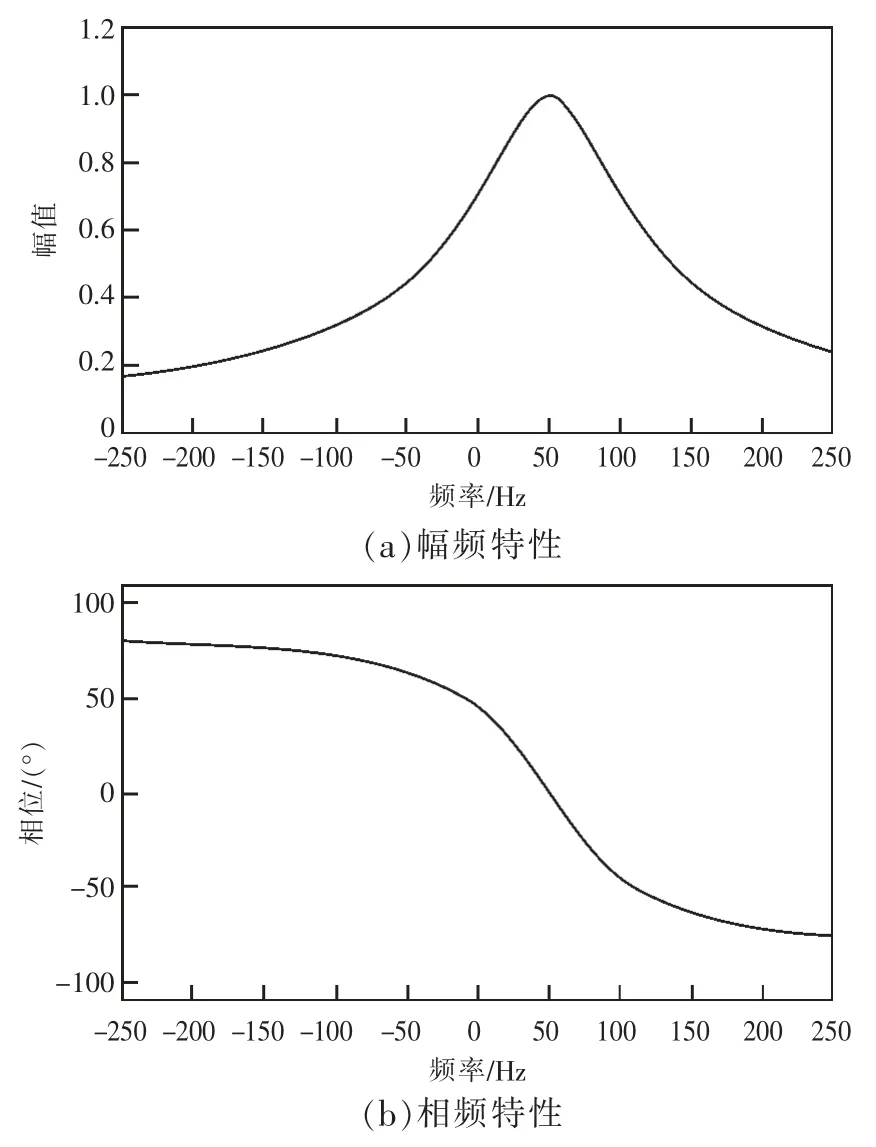
图2 一阶CCF 的伯德图

如图2 所示，假设指定频率为50 Hz，则50 Hz 分量将完全通过，而-50 Hz 分量将被减弱为，并且相位移为arctan（2ω0/ωc）。另外，谐波也会被减弱。CCF 和RCF（实系数滤波器）一样，在电网电压有不平衡和畸变时，会在提取精度和响应速度之间做个折中。和RCF 相比，CCF 有极性选择直接提取正、负序的优势。

1.2 MCCF 模型

理想状况下，在三相电网电压只有基波正序分量。但实际电网电压也许含有负序分量和谐波分量。假设一个三相三线系统，没有零序，三相电压Ua，Ub，Uc可以表示为式（2）：

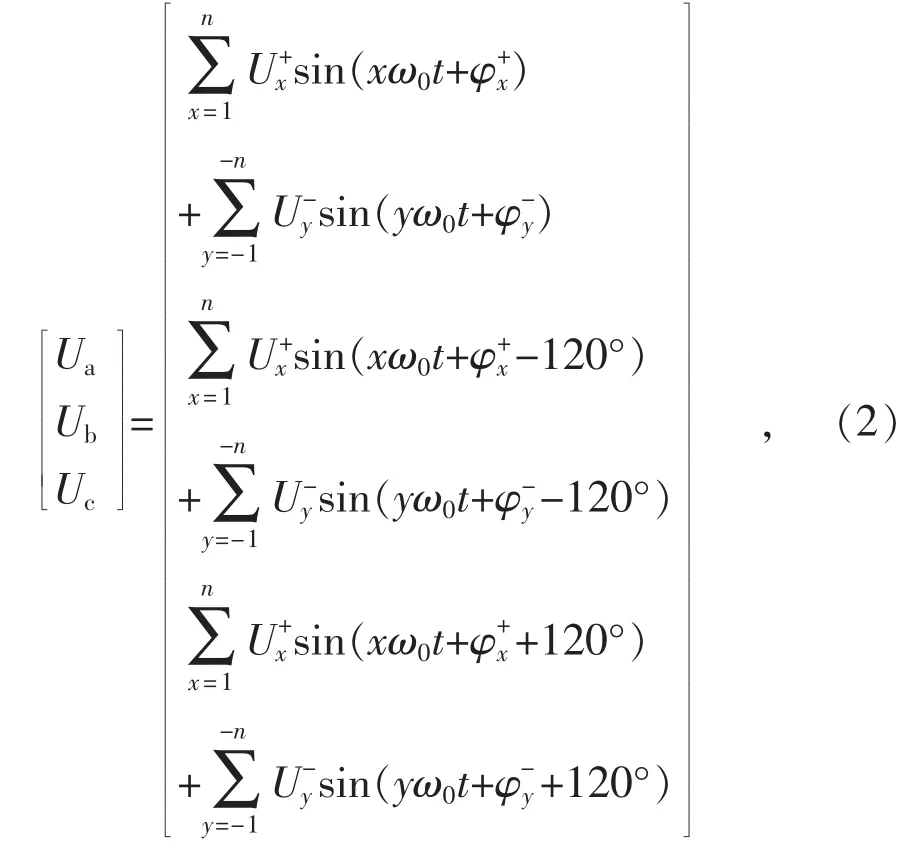
通过克拉克变换，式（2）可以表示为：

从上面推导可得：将abc 坐标系变为αβ 坐标系后相位差为90°，所以可用式（6）所示复数表示基波电压：

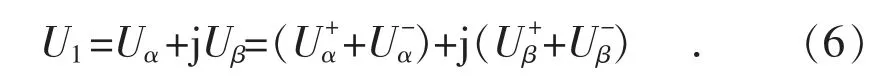
使基波正、负序分量和各次谐波正、负序分量以不同的角速度和旋转方向运动，同次谐波电压的正、负序分量是分别静止的。将基波正、负序电压乘以ejwt和-ejwt得到基波正、负序电压恒定直流量分别为，变换坐标如式（7）所示：

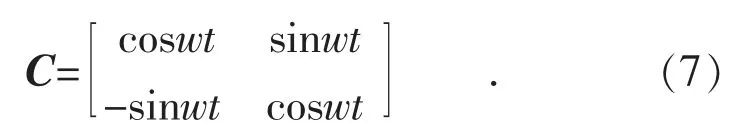
同理，将谐波正、负序电压乘以ejnwt和-ejnwt得到谐波正、负序电压恒定直流量。通过分离直流量再进行反变换，即可实现基波和各次谐波的精确测量。

胃窗超声造影对T4期的准确率高于超声内镜，超声内镜对T1期诊断准确率高于胃窗超声造影，具体结果见表3。

根据得到的基波和各次谐波的直流量及CCF的基本原理，可得MCCF 结构框图如图3 所示。

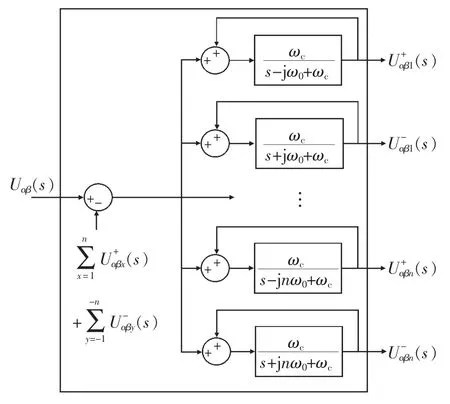
图3 MCCF 结构

通过图3 不难理解，将基波和各次谐波分离后的直流量分别作为输入量，再引入对应频率的正序或负序电压的反馈量乘以对应频率CCF 的传递函数可得基波及各次谐波的正序或负序分量的输出量。MCCF 数学模型如式（8）所示：

图4 MCCF 的子模块结构

根据式（8）得到对应的时域表达见式（9）：

2 基于MCCF 的同步信号检测系统的仿真建模

为了验证基于MCCF 的同步信号检测系统的性能，在MATLAB 中建立了系统模型，分别对输入电压含有谐波、三相电压不对称两种情况进行了仿真。仿真结果主要包括频率、相位、正负序及各谐波幅值。

2.1 仿真模型建立

2.1.1 三相电源仿真模型

三相电源仿真模型如图5 所示。

2.1.2 MCCF 系统仿真模型

2.2 仿真参数和结果

基于MCCF 同步信号检测系统仿真模型参数如下：三相电源，电压标幺值1.0 p.u.，频率为50 Hz，初始相位为0；MCCF 模型，截止频率ωc为222 rad/s，最优阻尼比0.707ω0。

利用MATLAB/Simulink 得到不同情况下的仿真结果。

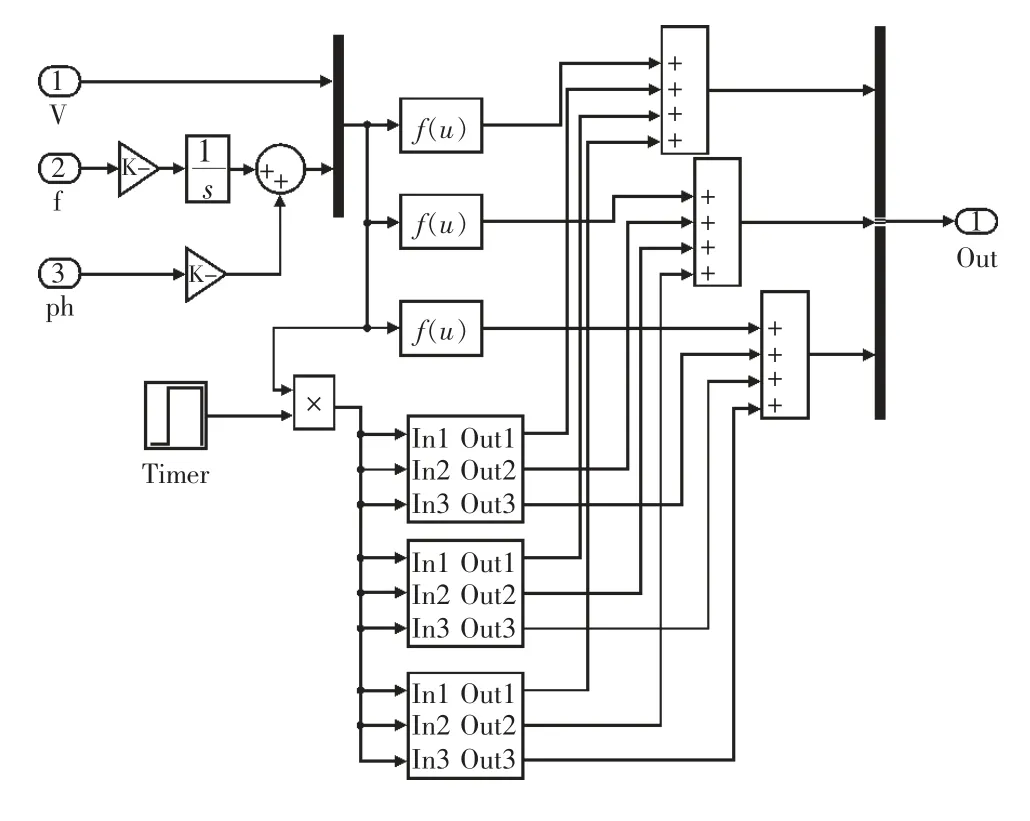
图5 三相电源仿真模型

（1）谐波条件下：在0.5 s 时加上标幺值为0.3的基波负序、标幺值为0.2 的5 次谐波和标幺值为0.1 的7 次谐波。仿真结果如图8 所示，可以看出，系统可以较快、较精确地提取出基波正序、基波负序、5 次谐波和7 次谐波分量的幅值、相位，响应时间约为30 ms。

图6 MCCF 仿真模型

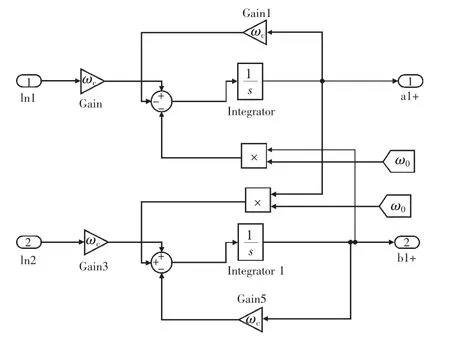
图7 MCCF 子模块仿真模型

（2）发生单相接地故障条件下：在0.5 s 时发生C 相接地短路。仿真结果如图9 所示，可以看出，在发生单相接地时，系统能够快速检测出基波正序、基波负序的幅值、相位、频率，响应时间约为30 ms。

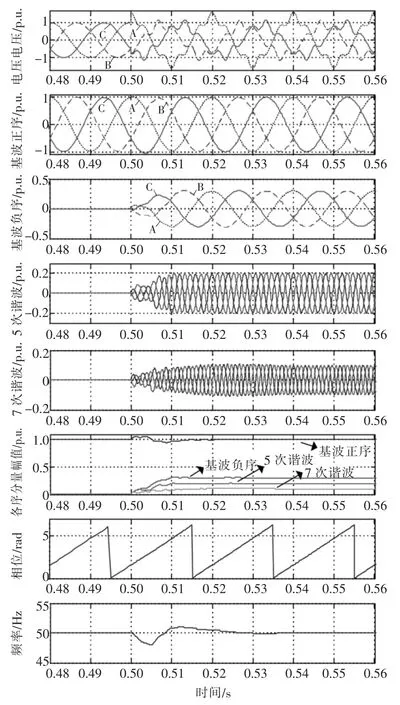
图8 谐波情况下的仿真结果

图9 发生单相接地的仿真结果

图10 两相电压跌落50%的仿真结果

（3）发生两相跌落故障条件下：在0.5 s 时发生B 相、C 相电压幅值跌落50%。仿真结果如图10 所示，可以看出，在发生两相跌落时，系统能够快速、精确地检测出基波正序、基波负序的幅值、相位、频率，响应时间约为30 ms。

由图8—10 可以看出，相比于之前提到的方法存在各种缺陷，本文提出的基于MCCF 的同步信号检测系统，无论在含有谐波或不平衡情况下都能够快速、精确地提取出基波正序分量、基波负序分量和它们的幅值。此外，还可估计得到谐波分量。

3 结语

本文简单介绍了电网同步信号检测技术在风电中的发展，然后分析了CCF 的频率选择特性和极性选择特性，比较了其与BPF 的优缺点。根据CCF 数学模型，提出了基于MCCF 的同步信号检测技术，并通过理论分析建立了MCCF 数学模型，最后利用仿真验证了技术的有效性。

由仿真分析可以得出：MCCF 具有频率选择特性和极性选择特性，可以在电网电压不平衡和畸变情况下，快速、精确地提取正、负序分量和其他谐波分量，因此在有源电力滤波器中具有很好的应用前景，在不理想条件下灵活控制风电三相并网变流器具有很大潜力。

同时MCCF 可以应用于锁相环技术上，以提高锁相环的锁相能力和精度。MCCF 和SRF PLL（基于同步旋转坐标系的锁相环）级联可以很好解决只用SRF PLL 锁相时基波负序造成的二倍工频波动分量，及其他谐波分量造成的纹波分量，因此所得结果精确度高。另外，它还可以被用于谐波分量提取、电能质量监测和孤岛检测等特殊要求下的同步信号检测。