基于刚度灵敏度矩阵的结构损伤识别

罗帅,杨浩,沈吉宝,侯刚,杨秋伟,李博

(绍兴文理学院 土木工程学院, 浙江 绍兴 312000)

0 引言

结构损伤识别的基本问题是如何从给定的物理参数测量中确定结构损伤的出现、位置和程度[1-2]。主流的损伤识别方法可分为基于动态响应的损伤识别方法和基于静态响应的结构损伤识别方法[3]，其中动态响应的损伤识别方法通过测试振动参数的变化以检测结构损伤状况[4]。但是在实际工程中需要采用昂贵的加速度传感器以获得结构在动态激励下的时程响应参数[5]，并且动态信号的处理往往需要分析结构的频率和振型变化[6]，这需要同时用到结构的质量和刚度矩阵[7]。此方法较为复杂且容易受到噪声干扰[8]，这给结构的损伤识别带来了困难。而基于静态响应的结构损伤识别则只需要测试外部静态荷载作用下的结构变形信息，测试技术成熟。其主要的难点问题在于所测试数据的分析，因此基于静态测试结果的结构损伤识别受到了广泛关注[9-10]。王艺霖等[11]基于位移影响线二次差值的概念提出了通过测量移动荷载下主梁跨中的竖向位移增量指标进行主梁结构损伤定位方法，该方法不适用于具有桁架结构的损伤识别。DOEBLING等[12]通过利用柔度矩阵分解的方法确定局部结构刚度以实现结构的损伤识别，该方法对超静定结构的分析结果误差较大。周卫东等[13]利用柔度矩阵求解公式，建立了结构单元刚度扰动参数和柔度扰动参数之间的对应关系进行结构的损伤识别的理论研究。MASOUMI等[14-17]利用推导的广义柔度矩阵进行结构的损伤识别，但是这类柔度识别的方法目前主要应用在具有单一类型构件的结构损伤识别上，对具有不同类型构件的结构系统的损伤识别尚需进一步研究。

本文开展了结构构件的损伤识别方法研究，引入灵敏度矩阵构建结构构件的损伤识别理论方法，建立结构构件损伤前后的变形差与损伤因子之间的函数关系，采用最小二乘法求解结构分析模型得到结构所有构件的损伤因子，实现构件的损伤定位和损伤程度定量分析。该方法主要针对结构外观检查难以发现的结构构件低水平损伤，识别精度高，方法简便可靠，同时本研究通过组合梁桥模型验证了所提出的构件损伤识别方法。

1 灵敏度矩阵及损伤识别方法

对于一个具有N自由度的结构系统，其静力平衡方程为

Ka·{Ua}={F},

(1)

其中:Ka是一个N×N阶的矩阵；{Ua}表示在静力{F}的作用下未损伤结构的N阶位移列向量，通常可以用理论模型求得。当结构发生损伤时，损伤后的平衡方程为

Kd·{Ud}={F},

(2)

其中:Kd是结构损伤后N×N阶的矩阵；{Ud}表示在静力{F}的作用下损伤结构的N阶位移列向量。

通常情况下，结构损伤总是以局部构件的刚度变化表现出来，因此可以将式(2)写成如下形式:

(Ka-Δk)·{(Ua+Δu)}={F}，

(3)

式(3)中的Δu为结构损伤后的结构结点位移向量差，可以表示为

{Δu}={Ud-Ua}，

(4)

式(3)中的Δk为损伤后结构的刚度矩阵变化，可以表示为

Δk=Ka-Kd。

(5)

假定构件单元在发生损伤时材料的刚度发生变化，损伤因子为βi，不妨将构件单元刚度矩阵损伤前后的Δk可以表示为[18-19]

Δk=βi·ki，

(6)

其中：ki(i=1～N)为有限元数值模型中第i个单元体的单元刚度矩阵；βi(i=1～N)为该单元体的损伤系数(0≤βi≤1)。将式(6)代入式(3)并对两边对于损伤系数βi求导：

(7)

忽略高阶项可得

(8)

整理式(8)得到

(9)

将式(1)代入式(9)中，可得

(10)

不妨将第i个结构单元刚度矩阵的灵敏度Bi表示为

Bi=Ka-1·ki·Ka-1·{F}，

(11)

当结构在发生损伤后，位移的变化量可以表示为

{Δu}={(Ua+Δu)}-{Ua}，

(12)

对式(12)进行Taylor展开，并取线性一阶微量，可得具有N个单元结构的位移变化量{Δu}为

(13)

将式(10)代入式(13)，可以得到具有整体结构损伤后位移变化关系

(14)

将式(11)代入式(14)中整理可得

(15)

将式(15)展开可以写成

{Δu}=B1·β1+B2·β2+…BN·βN，

(16)

其中:

(17)

位移变化量{Δu}可以实际测得，B可以采用式(11)求得。对于

{Δu}=B·{β}，

(18)

由于组合结构为超静定系统，因此灵敏度矩阵B不是满秩矩阵，可以利用最小二乘法求出其广义逆以求得损伤向量{β}:

{β}=B⊕·{Δu}，

(19)

其中:B⊕为灵敏度矩阵B的广义逆;{β}向量中的各元素即为结构损伤后构件的损伤系数。用静力加载所得结构基本响应参数进行损伤程度识别。

2 算例分析

2.1 结构模型简介

本文将所建立的损伤识别方法应用到结构的损伤识别中，针对如图1所示的结构模型开展基于刚度灵敏度矩阵的损伤理论研究。该结构的材料物理属性见表1。

图1 现场结构模型Fig.1 Photo of bridge structural model in experimental site

表1 材料物理属性Tab.1 Material properties

将结构模型简化为如图2(a)所示的平面结构模型，结点和单元编码如图中所示。该结构模型几何尺寸为3 000 mm×400 mm×400 mm，平均分成10跨；上下的纵向构件为梁单元，其余构件为二力杆，采用30 mm×18 mm×2 mm的双角钢制作。本文将结构模型划分为37个单元，其中①～⑩构件为梁单元，单元长度为0.3 m；其余的19个单元为杆单元，竖杆长0.4 m，斜杆长0.5 m，试验验证中的测点布置如图2(b)所示。

(a) 结点及单元排列

(b) 测点布置

2.2 基于刚度灵敏度矩阵的结构损伤分析

采用关联表法[20-21]建立各单元在整体坐标系下的单元刚度矩阵ki并集总形成结构在损伤前的整体刚度矩阵Ka，在跨中结点添加集中力为F=2 kN的竖向荷载。则由式(11)可得到结构系统的刚度灵敏度矩阵B。由具体工程实际可知，当结构发生大于20 %的损伤时，结构基本破坏且其损伤状况肉眼可见。故本文拟考虑4种观察不到的较小损伤工况：(1)单元21损伤12.5 %；(2)单元21和35刚度损伤12.5 %；(3)单元10和14分别损伤5 %、15 %；(4)单元9、12、19分别损伤3 %、20 %、10 %。采用数值模型求解整体结构的静力响应Ud。利用式(19)所推导的损伤识别方法求解结构构件的损伤因子，得到各损伤工况下结构的损伤因子如图3～图6所示。

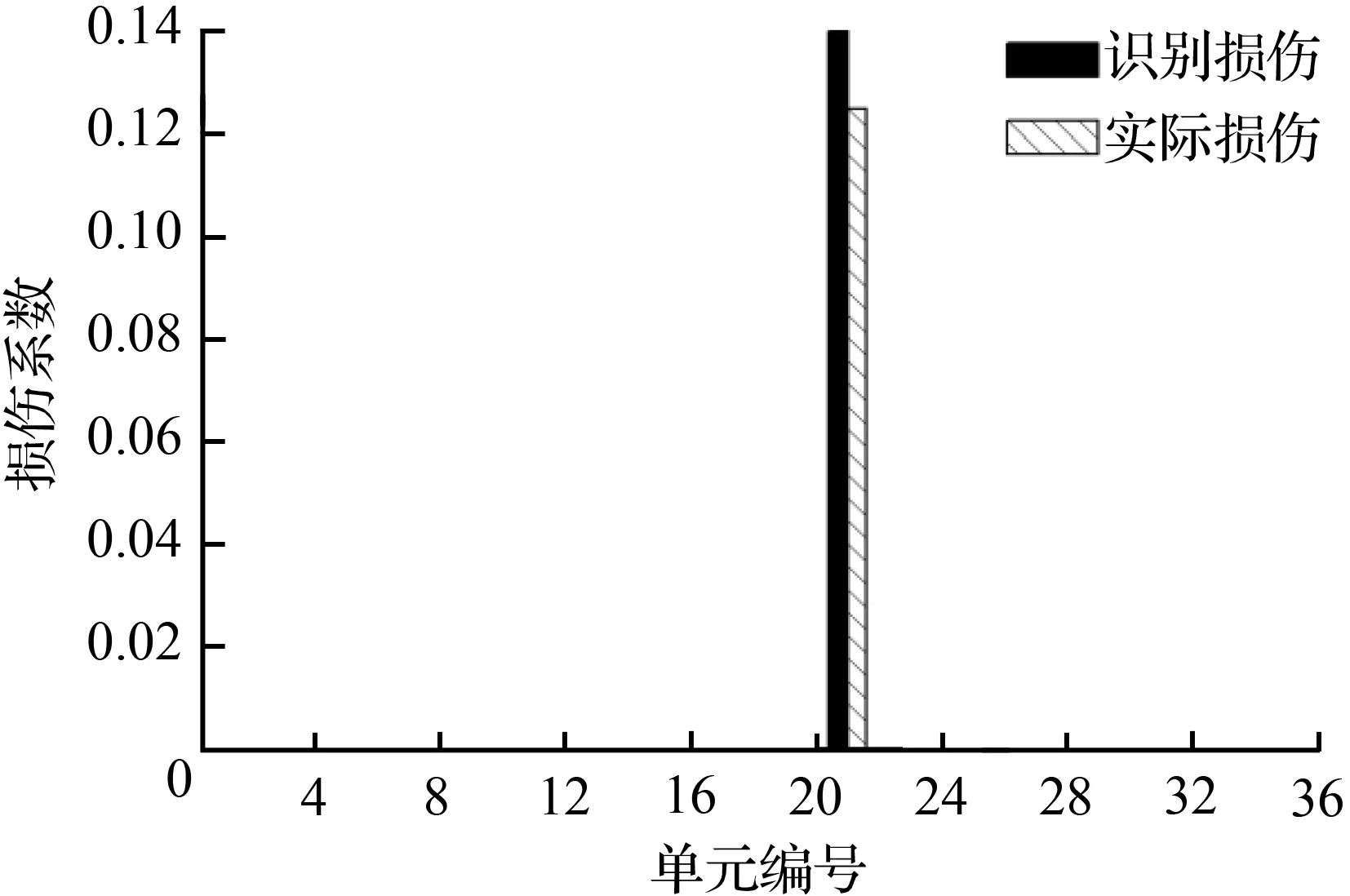
图3 单元21损伤12.5 %Fig.3 Element 21 damaged with 12.5 %

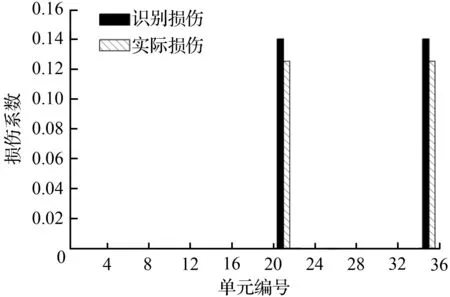
图4 单元21、35损伤12.5 %Fig.4 Elements 21 and 35 damaged with 12.5 %

图5 单元10、14分别损伤5 %和15 % Fig.5 Elements 10 and 14 damaged with 5 % and 15 %

图6 单元9、12、19分别损伤3 %、20 %、10 %

图3给出在工况(1)下单一构件基于刚度灵敏度的损伤识别最小二乘解(即式(19)的计算结果)与实际损伤程度的对比；图4和图5给出了在工况(2)、(3)下2根构件同时损伤时不同杆件损伤系数与实际情况的对比；图6给出了在工况(4)下3根构件同时损伤时基于刚度柔度灵敏度的损伤系数与实际情况的对比，具体数值误差量见表2。

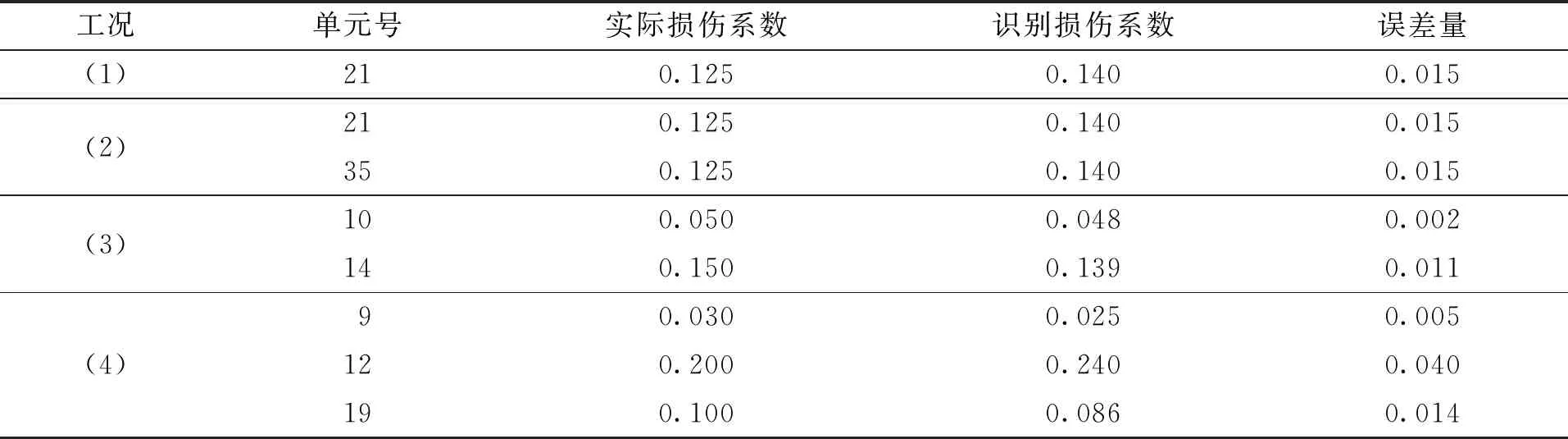
表2 实际与识别的损伤系数对比Tab.2 Comparison of damage coefficient between practice and recognition

从表2可知，在4种工况下的实际损伤系数与识别损伤系数存在较小的误差量，造成的原因是在求解损伤系数时，式(18)对于求解m×n维的矩阵方程采用的最小二乘法是一个误差最小的近似解，会对结果造成影响。通过实际和识别的损伤系数对比，也说明了这些微小误差的存在。刚度灵敏度矩阵方法为实际工程中及时监测构件的损伤，为结构安全提供良好的健康监测保障提供了可靠的分析方法。

3 试验验证

3.1 数值模型验证

为了验证理论模型的分析结果，在实验室中制作的结构模型与数值模型一致。如图7所示，结构模型底部采用工字钢将两榀钢桁架相连接，工字钢顶部铺设导轨，加载小车(质量约20 kg)可沿导轨运动，通过在小车上添加配重块加载，配重块质量：10 kg/件，施加与数值分析模型一致的荷载大小，放置18件配重块在小车上，总质量为200 kg。因结构模型结构是10跨对称结构，所以位移测点的布置是沿下部梁构件的4、5、7、9、10号结点处布置百分表测量结点的竖向位移变化量，百分表量程为0～10 mm，精度为0.01 mm。测点布置图如图2(b)所示。

图7 实验室结构静力加载试验Fig.7 Structure model static loading tests in laboratory

测试完好结构在静力荷载下结点的竖向位移，添加外荷载时将小车移动至6号结点施加静载，读取的结点位移变化值见表3。

表3 理论值与实测值对比表Tab.3 Comparison table of theoretical and experimental data

对比表3中理论值与实测值可知，选定结点的测试位移比理论模型的计算结果存在不到3 %的相对误差，说明理论模型的分析结果能准确反映实际情况。实测位移总是比理论模型的结果要大，造成的原因可能是实际结构中单元间的连接不能达到理想的刚性连接状态，因此数值模型的刚度大一些，造成实测的位移较理论值略大。

3.2 损伤分析结果验证

利用结构模型分别进行数值分析中工况(1)和工况(2)试验验证，单元的损伤程度通过改变构件的截面以确定其实际的损伤系数。由于结构模型构件都采用角钢拼接，因此可以在试验过程中，采用不同厚度的角钢组合以实现损伤程度的改变，替换的角钢如图8所示(损伤后构件双角钢采用(2 mm+1.5 mm)组合)，通过改变角钢厚度使替换后的构件刚度矩阵减少12.5 %，即损伤因子取为0.125。

图8 角钢对比图Fig.8 Comparison of angle steels

参考工况(1)，进行21号杆单元刚度损失12.5 %的损伤测试，荷载值及加载点与理论模型相同，如图9所示，贴纸处表示损伤构件。

图9 损伤结构静力加载试验Fig.9 Damaged structure static loading tests

表4为加载后结点竖向位移读数与采用数值模型理论分析的位移结果，对比可知，对于单一构件的损伤情况，理论模型能够实现损伤后的变形分析与实际情况保持一致。

表4 理论与实测值对比表Tab.4 Comparison table of theoretical and experimental data

参考工况(2)，进行21号和35号杆单元刚度同时损失12.5 %的静载试验，位移测点保持不变，结果见表5，对比可知，对于多根构件同时损伤的情况，理论模型能够用来分析实际的损伤情况，因此所建立的数值模型是合理可行的。

表5 理论与实测值对比表

通过对工况(1)、(2)的损伤试验，总体上试验的结果能较好的验证理论推导结果。不论是单一构件还是多个构件发生损伤，都能够对损伤程度有一个较好的识别结果，且其中实验实测值与理论计算值误差都基本低于4 %，这说明了刚度灵敏度矩阵识别损伤在实际工程中的可应用性。

4 结论

本文基于静态响应参数进行结构构件的损伤定位和损伤程度定量识别，利用所建立的刚度灵敏度矩阵与结构变形之间的函数关系求解构件的损伤因子，实现了结构的构件损伤定位和损伤程度定量识别。可以得到如下结论：

① 本文所提基于结构刚度灵敏度矩阵的损伤识别方法，可以较好地分析结构在发生不易观测损伤时的损伤程度，实现复杂结构的损伤精确定位和损伤程度定量识别。

② 通过对结构模型的损伤试验验证，测得的结构损伤后静力响应与理论分析情况基本吻合，试验结果验证了本文所提方法的有效性和实用性。

③ 对于难以通过外观检查发现的微小损伤识别计算过程简明，不需要求解非线性方程或迭代运算即可获得良好的结果，适用于具体实践中。