液态金属磁流体发电系统低电压高变比能量收集电路设计

2020-04-13张云睿张一鸣高俊侠

通信电源技术 2020年4期

张云睿，张一鸣，高俊侠，张雨

（北京工业大学信息学部，北京 100124）

0 引言

法拉第最早提出磁流体发电原理。1959 年，美国阿夫柯-埃弗雷特团队的实验室11.5 kW 磁流体发电实验装置首获成功，自此世界许多国家都投入了对磁流体发电技术的研究中[1]。磁流体发电技术主要分为液态金属磁流体（LMMHD）发电和高温等离子体磁流体发电两种[2]。其中，高温等离子体磁流体发电主要应用于火力发电站；而LMMHD 发电技术在应用要求上更加简单，应用面更加广泛，尤其适用于微小机械波的动能收集。2005 年，中国科学院电工研究所首次提出将液态金属磁流体技术应用于波浪能发电[3]，并分别于2008 年与2011 年研发出200 W 左右输出功率的原理演示装置和2 kW 的波浪能发电实验室样机[4]。

目前，LMMHD 发电技术仍然存在许多问题[5]。为了提高液态金属磁流体发电系统的效率，研究焦点多集中在换能装置的结构设计与改进方面。此外，由于液态金属磁流体发电系统低电压、大电流以及易受负载波动影响的电源特性，导致能量收集十分困难。本文首先对发电源特性进行分析，设计适用于LMMHD发电系统的能量收集电路，并通过Matlab Simulink 仿真验证了设计的合理性。

1 液态金属磁流体发电介绍

1.1 LMMHD 发电原理

与传统发电机利用导线切割磁场发电相比，相同点是LMMHD 发电方式也是基于法拉第电磁感应原理进行发电，不同点在于LMMHD 发电方式的发电介质为液态金属磁流体[6]。

发电原理如图1 所示。有效磁感应强度B作用于发电通道，发电工质以速度v流经发电通道，在磁场下受洛伦兹力作用下内部电子定向移动，产生电流，并通过位于发电通道x轴方向两侧壁上的金属极板输出，驱动负载。

图1 中l、a、h分别为发电通道的有效长度、有效宽度和有效高度。

根据法拉第电磁感应定律，可以计算出LMMHD发电参数。

图1 LMMHD 发电原理

空载电动势E为：

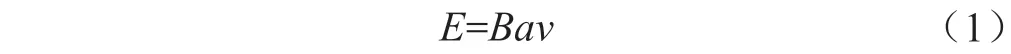
短路电流Imax为：

发电系统内阻Rg为：

负载电压UL为：

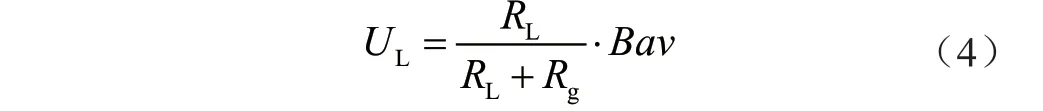
负载电流IL为：

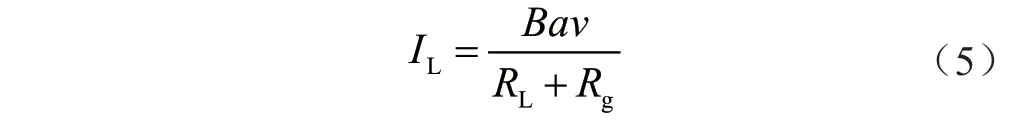
输出功率PL为：

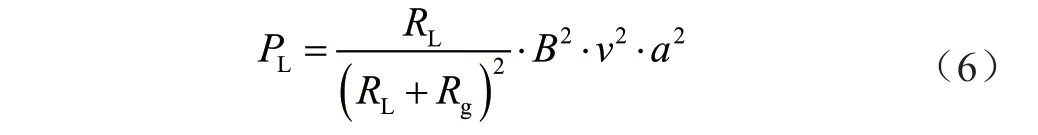
其中，式（1）～式（3）中σ为液态金属电导率，单位S·m-1。

1.2 LMMHD 发电系统电源特性分析

由式（1）～式（6）可计算出输出功率PL与负载RL的关系，如图2 所示。当负载与内阻相等即RL=Rg时，系统输出功率最大。实际上，由式（1）～式（3）可以发现，系统的内阻非常小为μΩ 级别，文献[11]也反映了这一点，很难做到负载等于甚至小于内阻值。因此，降低负载值成为提高系统输出功率的主要途径。

图2 负载-输出功率关系曲线

LMMHD 发电系统具有的内阻极低、输出电压低、电流大、变化频率低的特性。理想情况下，LMMHD 发电系统的发电效率高、环境兼容性强、维护成本低、兼容性高且稳定性强[7]。实际上，目前已有LMMHD发电系统的效率很少能到达60%以上[8-10]。影响LMMHD 发电系统效率的原因[8-10]之一是共轭阻抗匹配是否适当。

Boost 变换器既能实现升压又可以调节阻抗特性，可以很好地满足LMMHD 发电系统的电压小、电流大、变化频率低的输出特性的匹配性要求。能量收集电路设计方案如图3 所示。根据发电工质的流动方向，可将LMMHD 发电系统发电方式分为双向式与单向式。前者产生的为交流电，后者产生的为直流电。本文讨论的前提是同步整流器理想或者在单相发电方式下进行的能量收集。

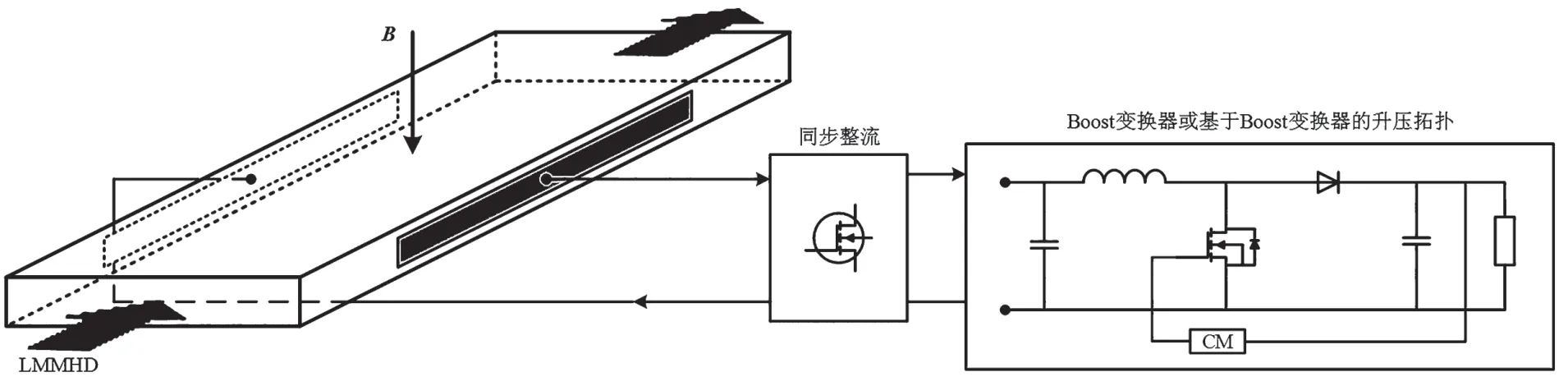
图3 LMMHD 发电系统能量收集方案示意图

2 能量收集电路分析

2.1 单级式Boost 变换器阻抗分析

电感、电容存在寄生电阻，半导体开关器件理想且工作在CCM 模式情况下，通过状态空间平均法对Boost 变换器进行建模。Boost 变换器电路如图4 所示，Boost 变换器在一个周期内的两个开关工作状态，如图5 所示。

由开关变换器的状态平均模型，可推导出Boost 变换器的状态空间平均方程，其中D'=1-D，且有：

图4 Boost 变换器电路

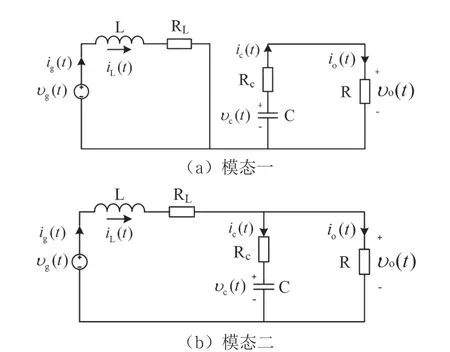
图5 Boost 变换器在一个周期内的两个开关工作状态

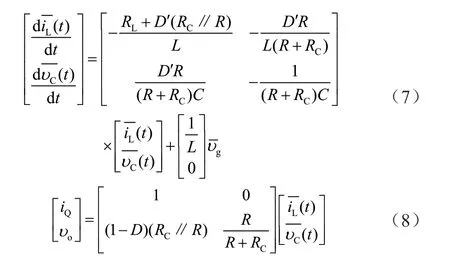
可得Boost 变换器状态空间平均等效电路模型与等效理想变压器电路模型，如图6 和图7 所示。

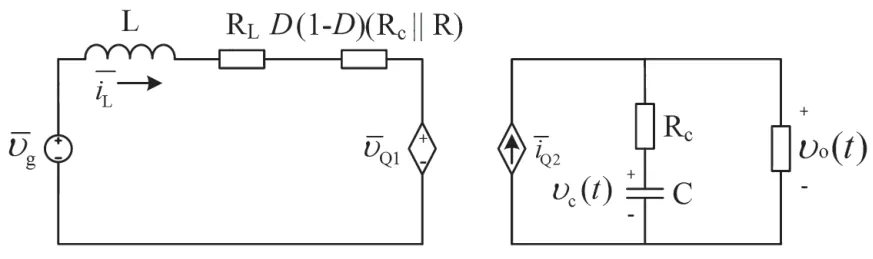
图6 状态空间平均等效电路模型

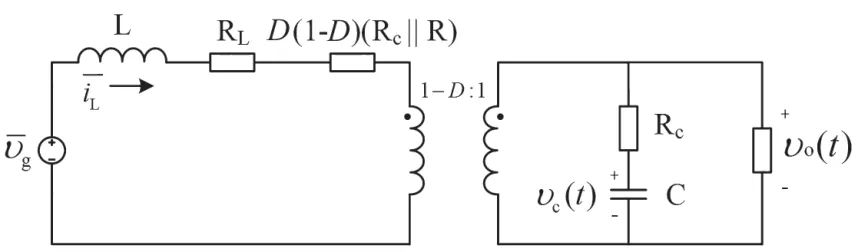
图7 等效理想变压器电路模型

由电路模型可直接求得开环输入阻抗表达式：

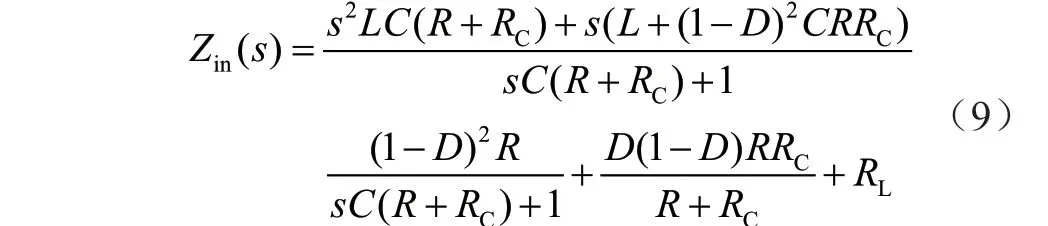
理想情况即RL=RC=0 下，开环输出阻抗为：

同理，可得开环输出阻抗表达式为：

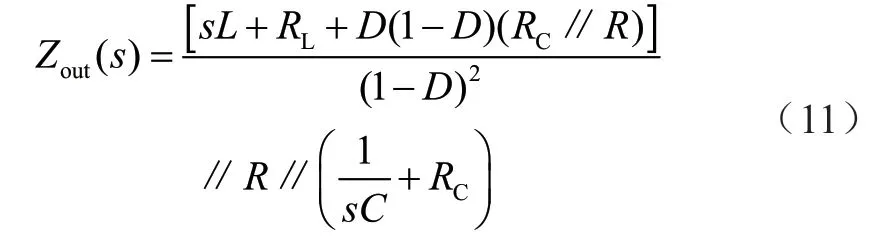
由式（9）、式（10）和式（11）可知：Boost 变换器输入阻抗大，可以有效钳位输入电压，获取更多的输入功率，输出阻抗低，有利于输出更大功率；趋势上，随开关频率的升高，输入阻抗变大，输出阻抗降低。

因此，在不考虑电路损耗情况下，Boost 变换器的开关频率越高，输入阻抗越大，输出阻抗越低，更易于获得较大的输出功率，并降低损耗。当考虑元件寄生参数损耗时，由式（11）可知，过高频率会增加系统的输出阻抗。

2.2 单级Boost 变换器局限性

若仅考虑电感串联电阻损耗，则根据Boost 变换器基本参数关系可以推导出：

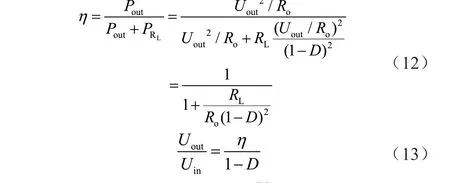
图8 理想情况下与实际情况下电压传输比与开关管占空比关系曲线

图8 表明：电感等效串联电阻限制了Boost 变换器的电压传输比。实际上，开关管的导通、关断以及开关损耗也进一步抑制了电压传输，因此在应用上Boost变换器的电压传输比一般为2～5。LMMHD 发电系统输出电压通常在0.2 V 左右，从电压存储角度分析，传统Boost 变换器可将电压提升至1 V 左右。这一电压而对于锂电池存储来说依旧不够，因此需要进一步提高变换器电压传输比。

3 多电平Boost 变换器应用

提高开关频率将增加变换器的开关损耗。提高电压传输比，需要提升占空比D，限制了上限开关频率。为了解决单级Boost 变换器升压不足和占空比过高的问题，采用Boost 变换器ISOP 组合[11]方案，即多电平Boost 变换器。以两级Boost 变换器ISOP 方案为例，拓扑结构如图9 所示。

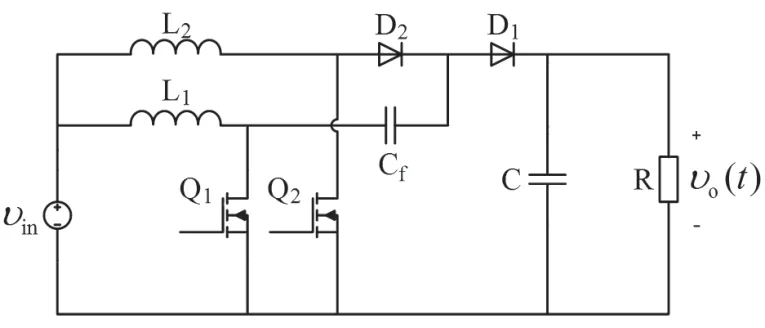
图9 含单个飞跨电容的并联交错型三电平Boost 变换器

根据电感伏秒平衡原理，有：

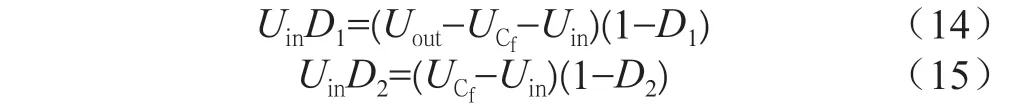
由式（14）和式（15），可得：

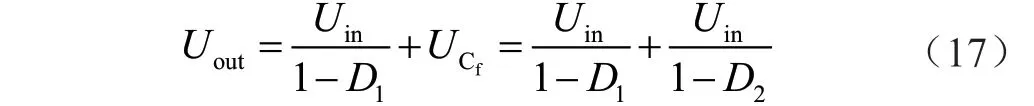
当D1=D2=D时，有：

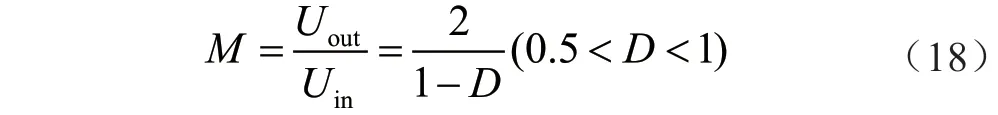
同理，可得n 组Boost 变换器[12]进行级联，如图10 所示。

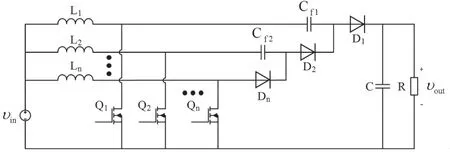
图10 有n 组开关网络的并联交错型高升压比Boost 变换器

当开关管开关占空比都相同时，元件基本参数一致且理想情况下，有：

但图10 多电平Boost 变换器存在如下弊端：（1）驱动管过多，开关损耗增加；（2）占空比取值受限；（3）开关管控制时序复杂。

在此考虑采用基于二极管-电容倍压器的结构（Diode-Capacitor Multiplier，DCM），对Boost 电路进行改进，如图11 所示。

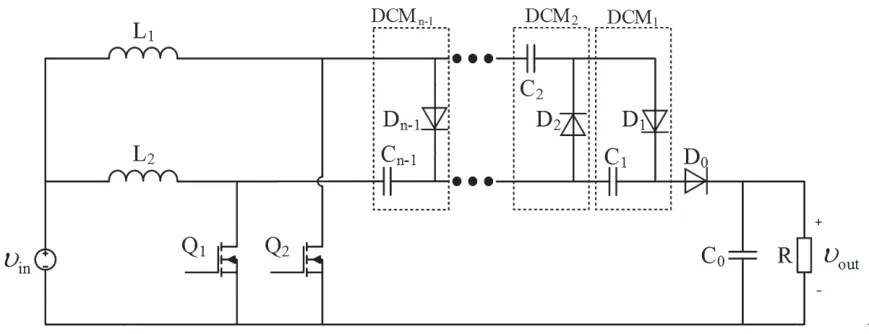
图11 带有n-1 组DCM 的高升压比Boost 变换器

它的原理是通过DCM 网络中电容的周期性自举使电压叠加达到升压效果。当L1=L2、D1=D2且元件参数理想时，根据拓扑结构推得其电压传输比为：

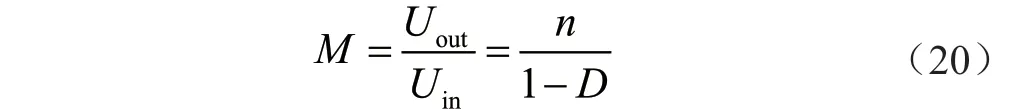
电压传输比M与D随n变化的关系，如图12 所示。

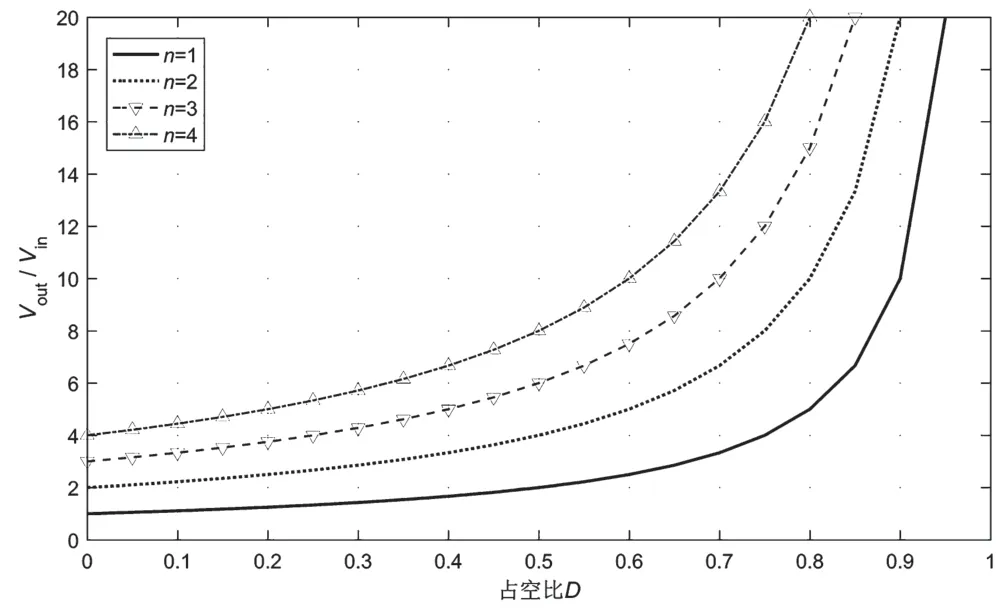
图12 不同n 值时电压传输比M 与占空比D 关系曲线

图11 说明，提升n可以有效降低开关管开关占空比D，增加了系统的闭环占空比调节裕度，提高了系统的整体抗干扰性。

4 设计与Matlab 仿真分析

参考文献[13]中LMMHD 发电系统进行能量收集电路设计，LMMHD 发电系统参数如表1 所示。

表1 LMMHD 发电系统主要参数

选择3.7 V 锂电池组进行储能，其充电电压设定为4 V 恒压充电。由式（20）计算得：电压传输比M=20。

传统单级Boost 变换器无法实现如此高变比。当设定占空比D=0.8 时，根据式（19）和式（20），可得n=4。考虑到交错并联型多级Boost 变换器的局限性，因此采用DCM 组合结构Boost 变换器方案进行设计。设计参数如表2 所示。

表2 3 组DCM-Boost 变换器组合能量收集电路基本参数

按此参数进行建模，模型如图13 所示。

开关管驱动信号波形及仿真结果，分别如图14 和图15 所示。

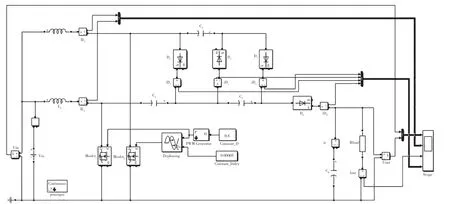
图13 基于三组DCM 结构的交错型Boost 变换器Simulink 模型

图14 开关管驱动信号波形

图15 仿真结果波形

图15 仿真结果表明，在开环占空比D=0.8 时，基于3 组DCM 结构的交错型Boost 变换器实现了20 倍电压传输比，电压提升至4 V，后级充电电流约为12.5 A，输出功率为50 W。与传统Boost 变换器相比，它有效降低了同等电压传输比下的开关占空比。通过两组充电回路，降低了系统的电流应力。