顾客策略行为下差异产品两阶段定价模型研究
2020-04-13杜宛京王海燕
马 鹏,杜宛京,王海燕
(1.南京信息工程大学管理工程学院,江苏 南京 210044;2.东南大学经济管理学院,江苏 南京 210096)
1 引言
目前,顾客策略行为的相关研究仍然是管理学界和相关企业关注的热点问题,如Zara,H&M,以及Home Depot等大型零售商通过使用价格优化软件来处理季末的产品,来应对顾客的策略行为。此外,在特定期限内零售商为自己出售的商品实行差价返还,也是应对策略性顾客的等待行为的一种途径[1]。
市场竞争的日益加剧使得产品更新换代的速度越来越快,零售商在销售期内也要根据市场情况及时改变定价策略来吸引顾客购买。例如,当新产品上市时,策略性顾客会选择等待观望而不是立即购买,那么在库存压力和产品更新换代的压力作用下,零售商会选择在第二销售期对新产品进行折扣销售,否则,产品的滞销会使零售商面临极大的损失。由于顾客策略行为的存在,零售商必须通过折扣降价来吸引消费者。而商家的频繁降价已将顾客训练的越来越具有策略性和选择性,表现为顾客会预期产品降价而选择等待一段时间购买折扣价格产品,以获得更大的消费者剩余。因此,零售商为了销售产品及获得利润最大化,定价决策时将顾客策略行为考虑其中就显得非常重要。
本文针对季节性产品,研究基于顾客策略行为的定价决策,季节性产品具有销售期相对较短,销售期末的产品残值较低等特点,因此常常采用正常销售和季末降价结合的方式。分别考虑只存在高质量的产品,以及同时存在高质量和低质量两种差异产品的情形。面对顾客的差异化需求,如何对差异产品进行定价成为零售商需要解决的首要问题,因为定价不当往往会导致消费者购买数量的减少,造成产品积压,产生库存浪费和资本占用。因此,考虑顾客对质量差异产品的策略选择行为,给出零售商最优的定价决策,将是非常值得研究的问题。
国内外关于顾客策略行为的文献很多,主要集中在以下两个方面:(1)基于顾客策略行为的定价和订货量决策,以及供应链协调的相关研究,例如:李钢和王勇[2]构建了一个由零售商和顾客群体组成的报童模型。Cachon和Feldman[3]研究了顾客策略行为下的价格承诺问题。Su Xuanming和Zhang Fuqiang[4]将顾客策略行为引入到供应链中,研究了顾客策略行为对供应链绩效的影响。杨光勇和计国君[5]进一步研究了顾客策略行为对竞争性供应链绩效的影响。王宣涛和张玉林[6]基于顾客策略行为的背景,研究了零售商具有公平偏好行为下的零售商最优决策及供应链协调问题。Ahmadi 等[7]研究了灰色市场和顾客策略行为下的批发价格契约和数量折扣契约。(2)基于顾客策略行为的动态定价的相关研究方面,官振中和任建标[8]将消费者的策略性行为和参考价格效应结合起来,研究消费者在历史和预期价格下零售商的动态定价策略。Kremer等[9]通过理论和实验,研究顾客策略行为对零售商动态定价策略的影响。Yan Bo和Ke Chenxu[10]研究了顾客策略行为下易逝品的两种动态定价策略。关于策略顾客行为下的跨期定价决策相关的文献有Su Xuanming[11],Liu Qian 和Zhang Dan[12],以及陈章跃等[13]。Su Xuanming[11]侧重于内生性跨期需求下的动态定价决策,而Liu Qian和Zhang Dan[12]考虑顾客策略行为下两个企业分别提供质量差异产品的动态定价竞争决策问题。陈章跃等[13]研究了顾客策略行为下的闭环供应链决策。本文主要考虑零售商销售一个高质量产品,以及同时销售高质量和低质量两种产品时的定价决策等两种情形。
关于差异产品定价决策的文献较为丰富。Parlaktürk[14]考虑一个企业向策略性顾客销售两种质量差异产品,得到企业和顾客之间博弈的均衡策略。Liu Qian和Zhang Dan[12]考虑两家企业提供垂直差异产品下的动态定价竞争问题。杜晓梦等[15]研究指出,消费者在接受和认知新产品时会面临新产品产生的不确定性和感知风险。颜荣芳等[16]研究再制造闭环供应链差别定价决策,并对如何提高闭环供应链的效率提出意见。林欣怡等[17]发现制造商可以通过收益共享契约制定合适的批发价和收益共享比率来协调整个闭环供应链。曹晓刚等[18]研究了新产品与再制造产品的质量和价格竞争的决策模型。随后,王文宾等[19]考虑新产品和再制造产品竞争环境下的逆向供应链奖惩机制。但是,以上文献很少考虑顾客策略行为。
以上关于顾客策略行为的研究主要侧重在定价和订购量决策,供应链协调以及动态定价,但是很少有学者涉及差异产品的定价策略,而本文重点考虑两个销售期情形下差异产品定价决策问题。因此,本研究进一步丰富了顾客策略行为下的定价决策理论与方法。另一方面,关于现实意义方面,该研究为零售商在面临策略性顾客时,确定最优的产品零售价格,获得最大销售利润提供了决策支持。因此,研究策略性顾客行为下差异产品的最优定价决策对于生产或销售单一产品或差异产品下企业的良好经营具有很好的指导作用,因此具有重要的现实意义。
本文在国内外关于顾客策略行为下差异产品的定价策略的研究和理论基础上,考虑两种情形,在第一类情形中,只存在高质量产品,根据顾客面对两个销售期的异质需求分别给出高质量产品的两阶段定价;在第二类情形下,市场上同时存在高质量和低质量两种产品。此外,在两种情形中,在第二销售期都考虑产品的跨期折扣因子。
2 问题描述与假设
目前市场上的服装等季节性产品,在经过一定的零售期后,其价格往往会大幅度下降。这主要是因为随着时间的变化,该类季节性商品在消费者心目中的价值会逐渐降低,此时商家会被动或主动地降低价格来吸引消费者,从而进一步提高销售利润。零售商此时面临的主要问题是,如何合理地调整价格,从而能够更好地迎合消费者心中对于产品的期望值,并获得利润最大化。
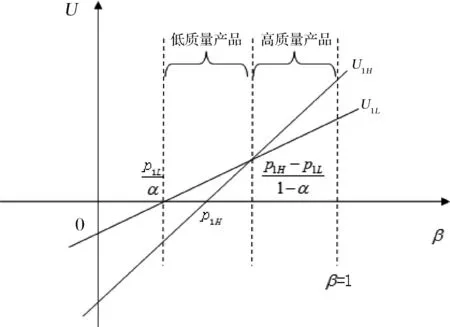
考虑消费者支付意愿β,为了进一步刻画消费者购买产品时的心理效用,建立相应的效用函数。顾客的效用函数由两部分组成——支付意愿β和产品价格pi,j(i=1,2分别表示第一、二销售期,j=H,L分别表示高质量和低质量产品)。在第一种情形中,市场上仅存在一种高质量产品,在经过一定销售期后,由于产品并未全部销售出去,因此零售商进行降价处理。此时消费者对于商品的整体效用评价会下降,把其下降的因子称为δ,即跨期折扣因子,满足0≤δ≤1(详细解释见假设4)。在另一种情形中,市场上同时存在高质量产品和低质量产品,并进一步地对其进行相应的价格调整,而消费者对于低质量产品的整体效用评价会低于高质量产品,为了方便模型的分析,在不失一般性的前提下,本文基于以下几点假设:
假设1:piH、piL分别表示高质量和低质量产品的零售价格,cH、cL分别表示高质量和低质量产品的单位生成成本,qiH、qiL分别表示高质量和低质量产品的销售量(i=1,2分别代表第一销售期和第二销售期)。
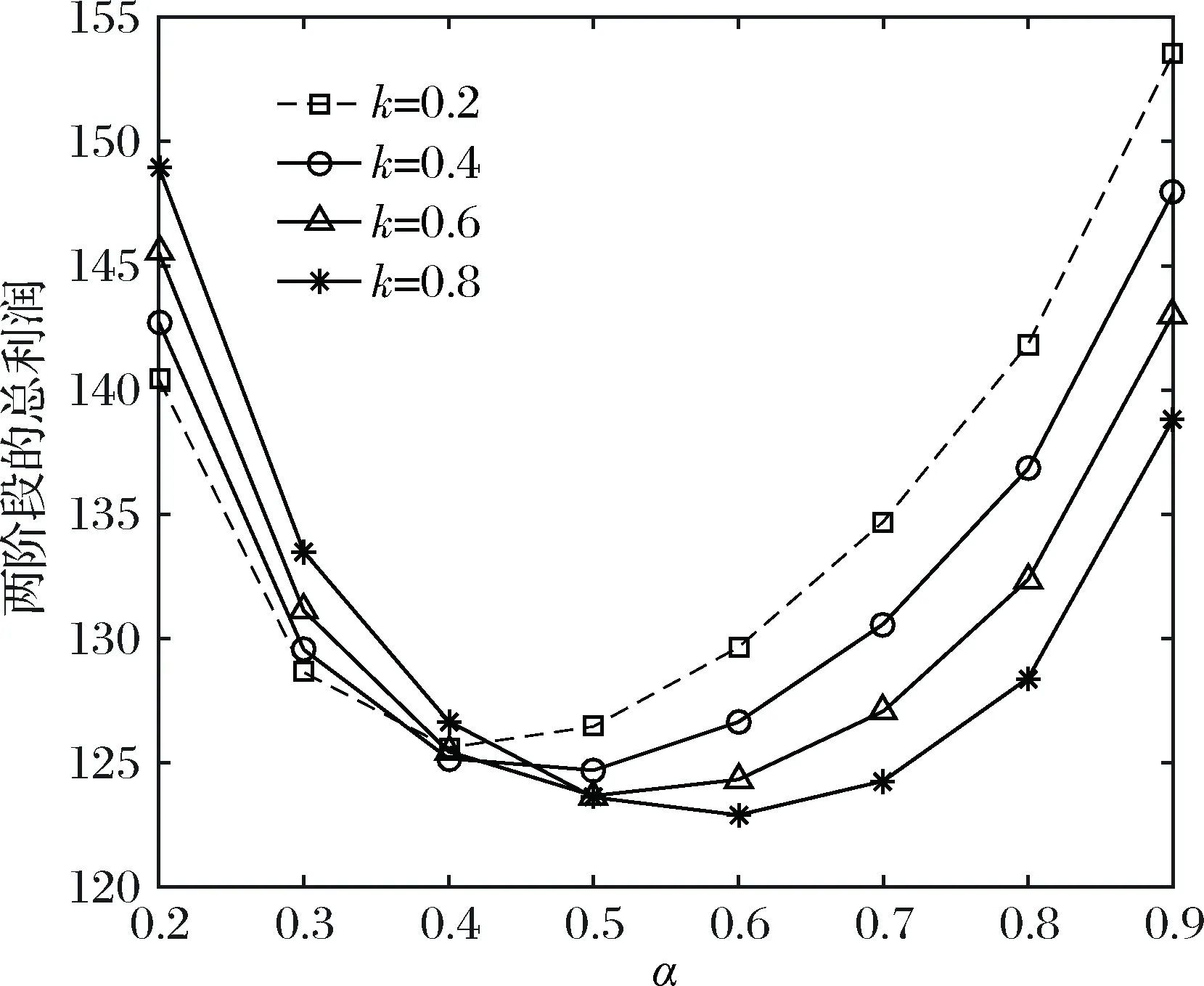
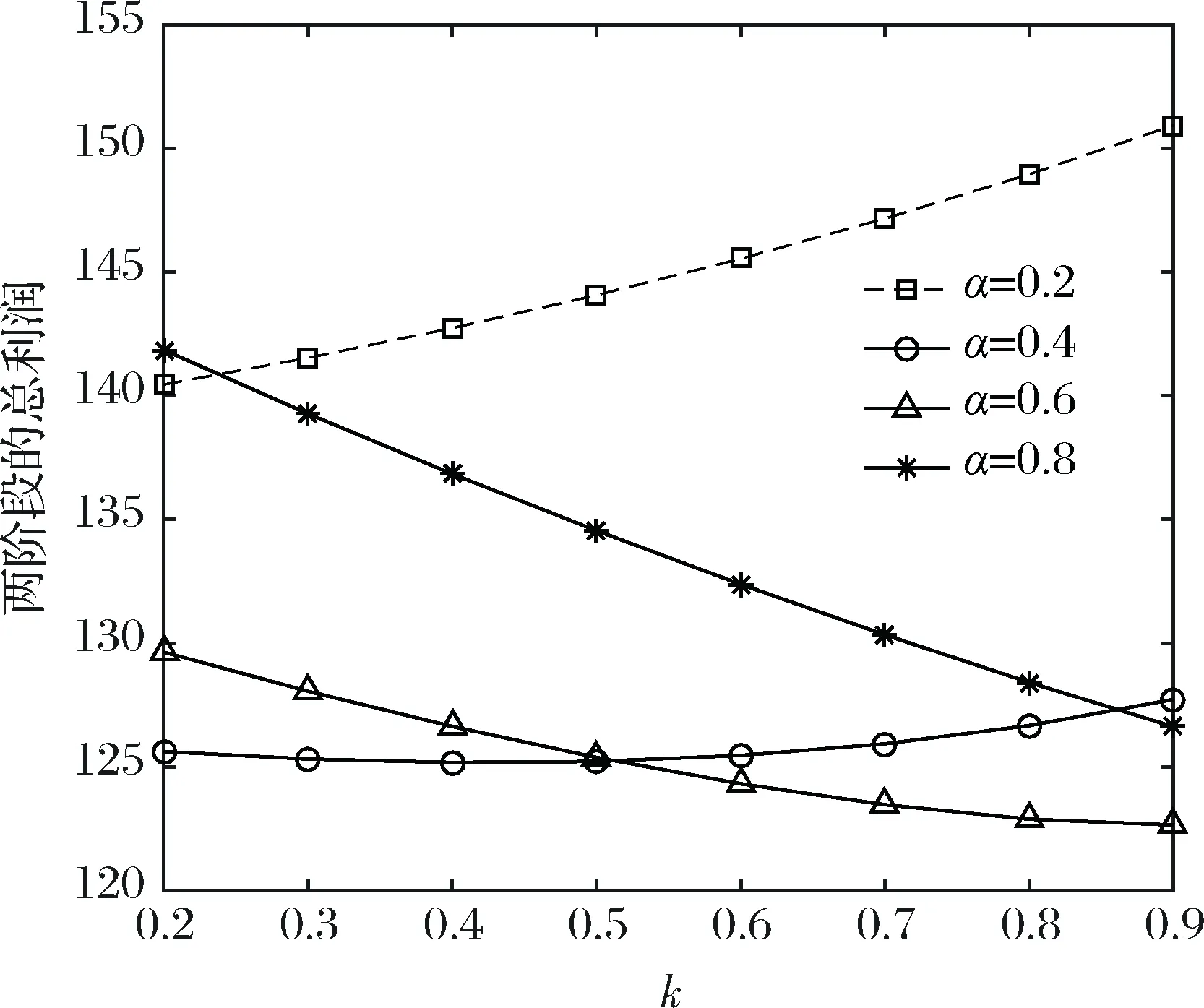
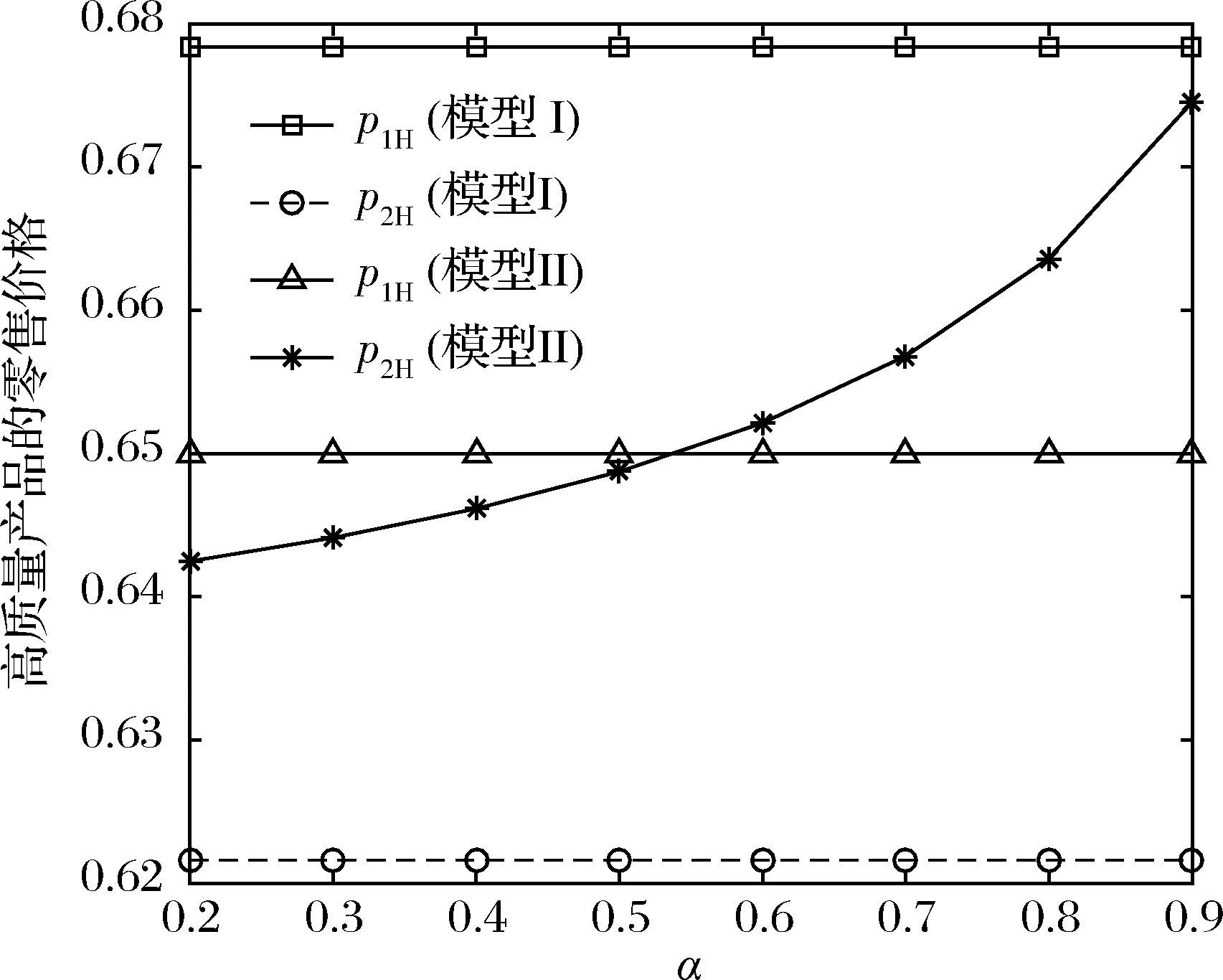
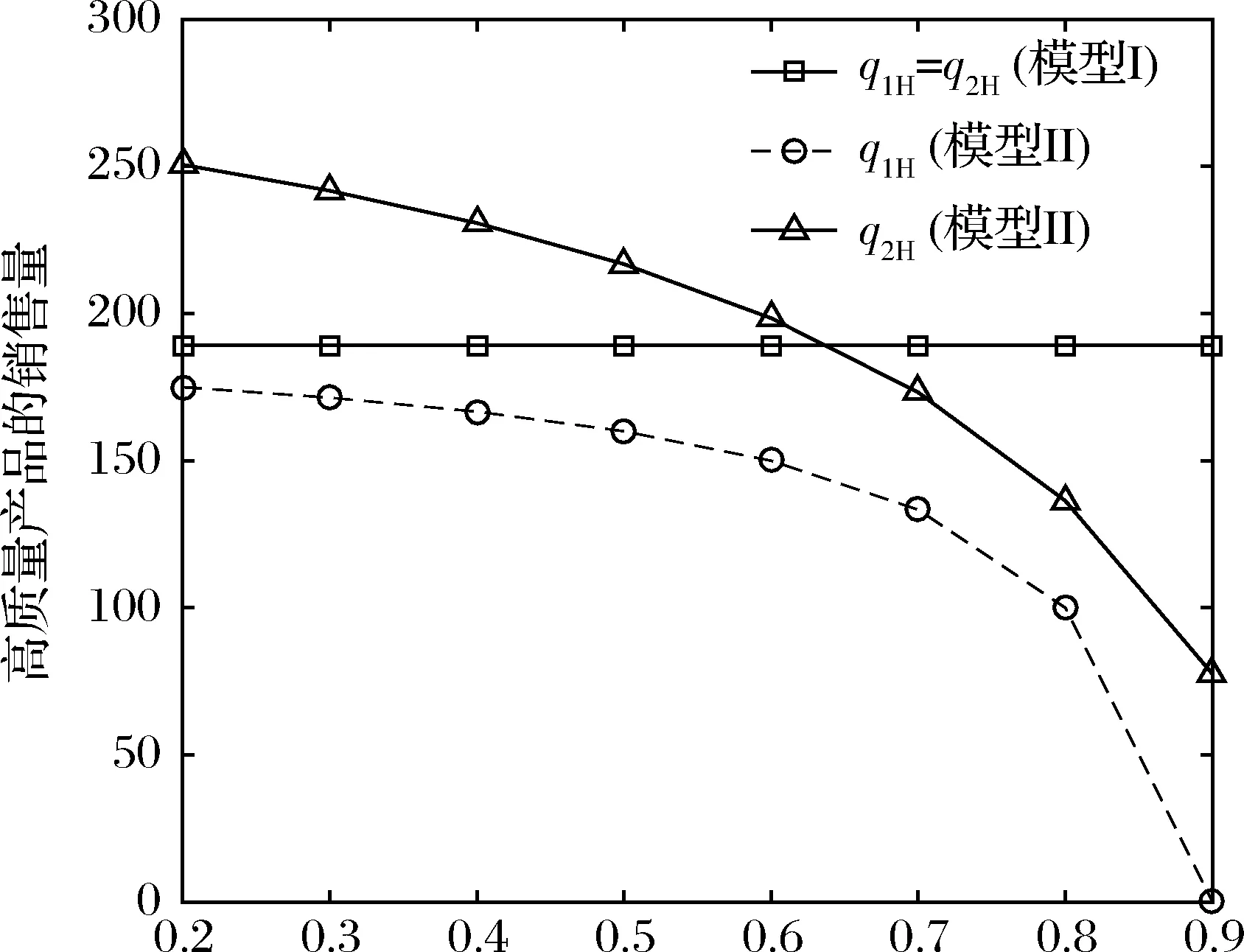
假设2:市场上该产品的潜在消费者总量为N,每个消费者只购买一件产品。当市场上只存在高质量产品时,消费者会选择立即购买,或者等待一段时间再购买;当市场上存在高低质量两种产品时,在产品销售初期购买产品的消费者占总量的比例为r(0 假设3:消费者对高质量产品的评价或支付意愿为β,其服从区间[0,1]上的均匀分布,αβ表示消费者对低质量产品的评价或支付意愿,其中α表示消费者对低质量产品的评价是高质量产品的评价的一个比例(α也可理解为消费者对低质量产品的接受度),即α∈[0,1]。也就是说消费者对低质量产品的评价比对高质量产品的评价低。在第二类情形下,在第一销售期,市场上同时存在高质量和低质量两种产品时,顾客选择购买高质量产品和低质量产品的效用函数分别为U1H=β-p1H,U1L=αβ-p1L。 假设4:类似于文献Liu Qian和Zhang Dan[12], 以及陈章跃等[13],购买高质量产品时顾客效用的跨期折扣因子为δ,(0≤δ≤1)。δ可以理解为顾客的策略程度,δ越大表示顾客的策略程度越高。δ=0,意味着只要顾客得到正的剩余,则顾客就会立即购买。当同时存在高质量产品和低质量产品时,在第二销售期,消费者心理对低质量产品的跨期效用评价会低于高质量产品,假设其跨期折扣因子为kδ,满足0 考虑市场上只存在一种高质量产品,产品价格随着时间的变化而变化,并且消费者对产品的效用也随着时间进行折扣,顾客在销售初期和销售末期的效用分别为: U1H=β-p1H (1) U2H=δ(β-p2H) (2) 图1 参数β与效用U的关系 由于β服从均匀分布,因此结合第一、第二销售期的效用函数(1)和(2),可得高质量产品第一、第二销售期的需求函数分别为: (3) (4) 高质量产品在第一销售期和第二销售期的利润函数分别为: Π1H=(p1H-cH)q1H (5) Π2H=(p2H-cH)q2H (6) 因此,零售商销售高质量产品在第一销售期和第二销售期的总利润为: Π=Π1H+Π2H=(p1H-cH)q1H+(p2H-cH)q2H (7) 分别求式(7)关于p1H和p2H的一阶导数,可得: (8) (9) 并且求Π关于p1H和p2H的二阶偏导数,可得: (10) 由式(10),可得Π的黑塞矩阵为: (11) 联立式(8)和式(9),可得: (12) (13) 将式(12)和式(13)分别代入式(3)和式(4)中,可得,高质量产品在第一销售期和第二销售期的最优销售量分别为: (14) (15) 将(12)-(15)代入到式(7)中,可得零售商销售高质量产品在第一、第二销售期的总利润为: (16) (2)高质量产品在第一销售期和第二销售期的最优销售量都是关于δ递减; (3)零售商利润(Π)随着跨期折扣因子δ的增加而减少。 由命题1可以看出,仅存在高质量产品的情况下,随着跨期折扣因子增大,产品在第一销售期降价变得快得多,产品在第二销售期价格关于跨期折扣因子递增。跨期折扣因子增大对产品的销量来说是不利的,且整个产品的销售利润随着跨期折扣因子的增大而减少。也就是说,跨期折扣因子对整个产品来说都是不利的。这是因为,当跨期折扣因子增大时,顾客的策略程度增大,使得更多的顾客选择等待购买,而不是立即购买,从而顾客中选择立即购买的人数减少,而选择等待购买的人数增加,因而顾客策略行为对零售商是不利的。因此,零售商应该采取一些打折,差价返还等市场营销策略来吸引顾客立即购买。 考虑市场上同时存在高质量产品和低质量产品,消费者会根据自身效用最大化在高质量产品和低质量产品之间进行选择。此外,随着时间的推移,顾客会在心理形成对高质量产品和低质量产品产生不同的跨期折扣因子δ和kδ。 (1)第一销售期的模型 顾客对高质量产品和低质量产品在第一销售期的效用函数分别为: U1H=β-p1H (17) U1L=αβ-p1L (18) 图2 参数β与效用U的关系 图3 参数β与效用U的关系 结合式(17)和式(18),可以得到高质量产品和低质量产品在第一销售期的销售量分别为: (19) (20) 其中,r为在产品销售初期购买产品的消费者占总量的比例。 零售商销售高质量产品和低质量产品在第一销售期的利润函数分别为: Π1H=(p1H-cH)q1H (21) Π1L=(p1L-cL)q1L (22) (2)第二销售期的模型 高质量产品和低质量产品经过一段时间的上市后,消费者对于这种产品的热情度会下降,会更理智的根据效用选择购买高质量产品还是购买低质量产品,同时会在心理上形成一种跨期折扣因子δ或kδ(0≤δ≤1),此时,消费者对高质量产品和低质量产品的效用函数分别为: U2H=δ(β-p2H) (23) U2L=kδ(αβ-p2L) (24) (25) (26) 其中,(1-r)为降价后选择购买产品的消费者占总量的比例。 零售商销售高质量产品和低质量产品的利润函数分别为: Π2H=(p2H-cH)q2H (27) Π2L=(p2L-cL)q2L (28) 联合式(21)-(22),以及式(27)-(28),可得两阶段销售期的两个产品的销售总利润为: Π=Π1H+Π1L+Π2H+Π2L (29) 为使获得的总利润最大化,分别求式(29)关于p1H,p1L,p2H,以及p2L的一阶偏导数,可得: (30) (31) (32) (33) 联立式(30)-(33),可得两种产品在第一销售期和第二销售期的最优零售价格分别为: (34) (35) (36) (37) 将式(34)-(37)代入到式(19)-(20),以及式(25)-(26)中,可得两种产品在第一销售期和第二销售期的最优销售量分别为: (38) (39) (40) (41) 将式(34)-(41)代入到式(29)中,可得高质量和低质量产品在第一、第二销售期的总利润为: (42) 对该情形下的最优解进行分析,可得命题2。 命题2:(1)在第一销售期,高质量产品的零售价格p1H与顾客对低质量产品的接受度(α)无关,而低质量产品的零售价格p1L随着α增大而增大。在第二销售期,p2H,p2L都随着α增大而增大。 (2)在第一销售期,高质量产品的销售量q1H随着α增大而减小。低质量产品的销售量q1L随着α的增大而增大;在第二销售期,高质量产品的销售量随着α的增大而减少,低质量产品的销售量是随着α的增大而增大。 证明: (k2cL+(-2cH+2cL+2)k+cL-2-2cH) 令H(k)=k2cL+(-2cH+2cL+2)k+cL-2-2cH,可得方程H(k)=0的两个根分别为: 因此,p2L和p2H都随着α增大而增大。 令 假设cH=0.3,δ∈(0.3,0.9),N=1000,且cL=0.2,r=0.4,以及α∈[0.2,0.9],考虑k=0.2,0.4,0.6,0.8,研究参数α对两阶段总利润的影响。发现:给定一个k值,两阶段的总利润随着α的增大先减小后增大,也就是说α越大或者越小,即两个产品差异较小或者两个产品差异较大,这种情况对企业来说是最有利的。α越小(α=0.2),说明两个产品质量差异越大,顾客在两个产品之间选择越来越固定,此时对零售商也是有利的,因为两个产品之间的竞争很小。如果α越大(α=0.9),两个产品质量差异越小,在第一销售期,高质量产品的零售价格与顾客对低质量产品的接受度无关,而低质量产品的零售价格随着α增大而增大。第二销售期的两个产品的零售价格都随着α增大而增大,从而导致零售商的利润增加。 此外,当两个产品差异较小时,如果消费者在第二阶段对低质量产品的跨期折扣因子相对较小(k=0.8),这样对企业来说是最有利的;当两个产品差异较大时,如果顾客在第二阶段对低质量产品的跨期折扣因子相对较大时(k=0.2),这种情况对企业来说也是最有利的。 图4 参数α对两阶段总利润的影响 当α=0.2,0.4,0.6,0.8,研究参数k对两阶段总利润的影响。发现:当两个产品差异较大时(α=0.2,0.4),两阶段的总利润随着k的增大而增大。反之,当两个产品差异相对较小时(α=0.6,0.8),两阶段的总利润随着k的增大而减小。对零售商来说,如果生产或销售的两个产品差异较大,则销售期末两个产品打折力度类似,这种策略对零售商来说比较有利。反之,如果生产或销售的两个产品差异较小,则销售期末两个产品打折力度差距较大,这样策略对零售商来说更加有利。 图5 参数k对两阶段总利润的影响 下面分别研究参数α对模型I和模型II中高质量产品的零售价格及销售量的影响。假设cH=0.3,cL=0.2,N=1000,r=0.4,δ=0.7以及α∈[0.2,0.9],图6显示: 模型I中的第一销售期的零售价格高于模型II中的零售价格,而模型I中的第二销售期的零售价格低于模型II中的零售价格。图7显示:当顾客对低质量产品的接受度增加时,模型II中的第一期和第二期的销售量都会减少。这是因为,当α增加时,在顾客的心中,高质量产品和低质量产品的差异变小,从而两个产品之间的竞争变大。 图6 参数α对零售价格的影响 图7 参数α对销售量的影响 本文研究了基于顾客策略行为的差异产品两阶段定价模型。首先,分析了只存在一种高质量产品的两阶段销售市场,找出其最优的定价决策,以及每一期最优的销售量。研究发现:(1)高质量产品在第一销售期的价格随着跨期折扣因子增大而减小,高质量产品在第二销售期的价格随着跨期折扣因子增大而增大。(2)高质量产品在两个销售期的销售量一致并随着跨期折扣因子增大而减小。(3)高质量产品的两阶段销售的总利润也随着跨期折扣因子增大而减小。 其次,研究了存在高质量和低质量产品的两阶段定价模型。发现:(1)第一销售期的高质量产品的零售价格与顾客对低质量产品的接受度(α)无关,而低质量产品的零售价格关于α递增。在第二销售期时,高质量和低质量产品的零售价格都是关于α递增。(2)在第一阶段,高质量产品的销售量随着α的增大而减少,而低质量产品的销售量随着α的增大而增大。在第二阶段,高质量产品的销售量随着α的增大而减少,而低质量产品的销售量随着α的增大而增大。 然后,数值分析了α和k对两阶段总利润的影响,发现:(1)α相对较小或相对较大时,对零售商来说比较有利,也就是说产品差异较小或者差异相对比较大时,对零售商来说是比较有利的。 (2)如果零售商生产或销售的两个产品差异较大,则销售期末两个产品打折力度类似,这种策略对企业来说比较有利。(3)如果生产的两个产品差异较小,则销售期末两个产品打折力度差距较大,这样策略对企业来说更加有利。最后比较了模型I与模型II下高质量和低质量产品的零售价格与销售量关于α的变化情况。3 模型构建与分析
3.1 零售商只销售高质量产品的情形(模型I)
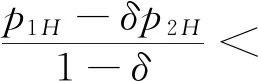
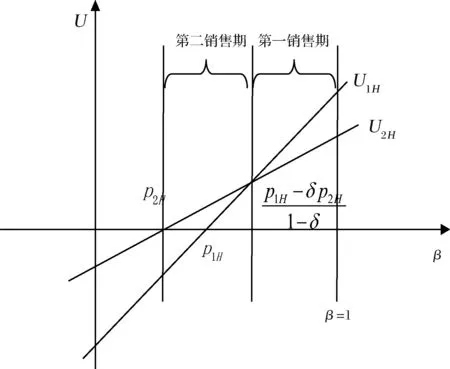
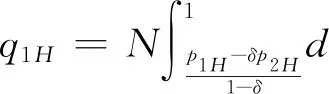

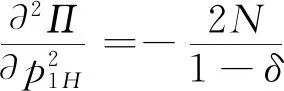
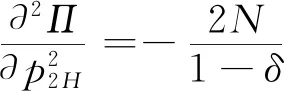
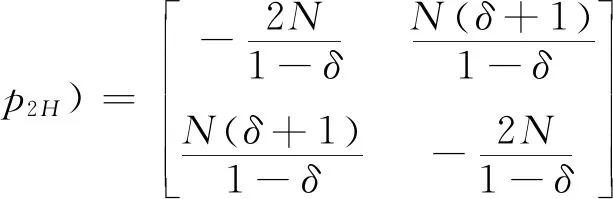
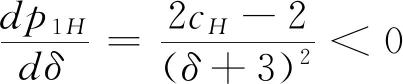
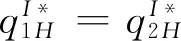
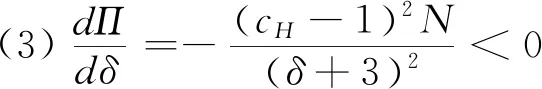
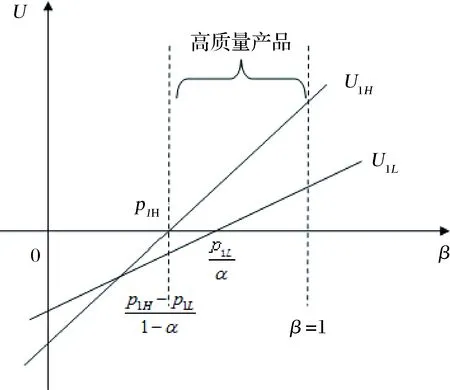
3.2 零售商同时销售高质量和低质量两种产品的情形(模型II)
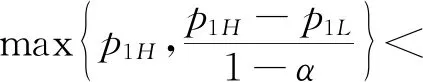
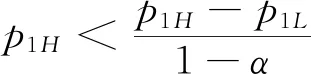
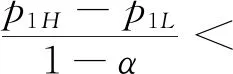
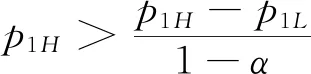
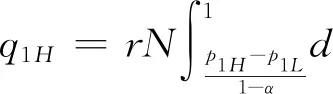
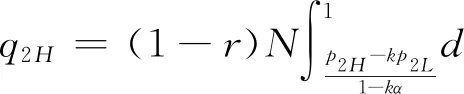
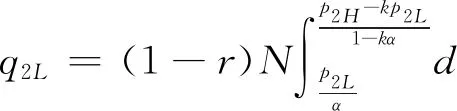
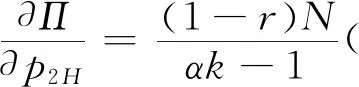
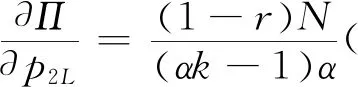
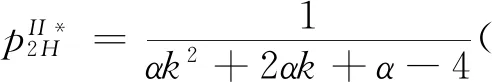
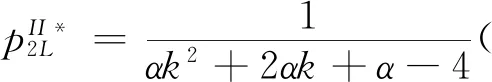
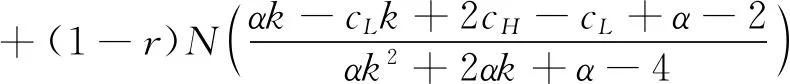
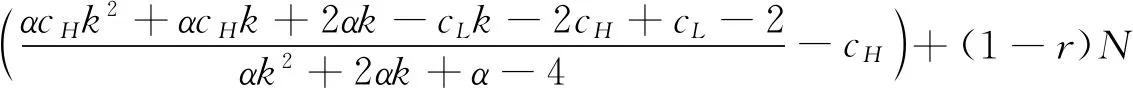
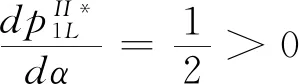
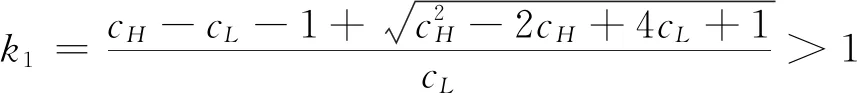
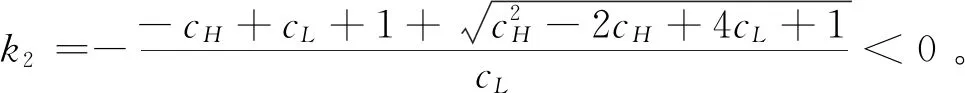
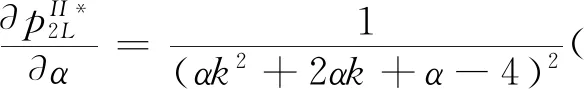
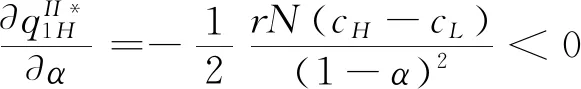
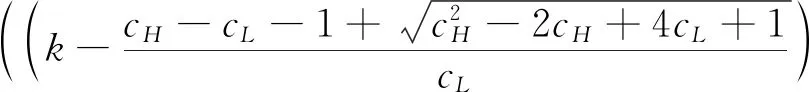
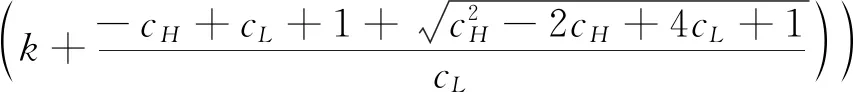
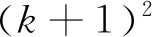
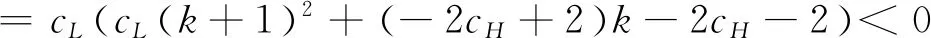
4 数值分析
4.1 参数α和参数k对两阶段总利润的影响(模型II)
4.2 模型I与模型II的对比研究
5 结语
