基于多级差分的双门限信道检测方法

谢慧明，覃 阳，杨 端

（1.桂林航天工业学院，广西桂林541000；2.桂林电子科技大学，广西桂林541000）

0 引言

数字信道化接收机具有宽带宽、大动态范围、高灵敏度、高实时性及全天候等优点,被广泛应用于电子对抗中的信号接收与识别、无线通信等领域中[1-2]。近年来，为应对密集环境下的信号识别与处理，动态数字信道化接收机应运而生。所谓动态数字信道化接收机就是将接收到的信号数字化后，经过均匀划分的数字滤波器组进行滤波实现子信道划分，然后对每个子信道的信号采用频谱感知的方法实现信道判别，根据判决结果构造新的数字滤波器组，实现非均匀数字动态信道化接收机[3-4]。由此可见，频谱感知是信道判别和非均匀动态数字信道化接收机的重要一环。近期关于非均匀动态数字信道化接收机的研究大部分都集中在滤波器的设计上，而对频谱感知技术方面的研究相对薄弱[2]。

最传统的频谱感知算法是能量检测算法[5-7]，能量检测算法计算简单快速，在工程上得到了广泛的应用，但是其检测性能较差，而且在不同子信道间噪声基底差异较大的情况下，性能下降较快。循环特征谱检测和基于拟合优度检测的子带频谱感知等算法[8-10]跟能量检测算法对比，能取得较好的检测效果，但是这类算法计算复杂度较高，不能进行实时处理，无法在FPGA上实现，而在FPGA上实现数字信道化接收机将能得到较快的处理速度，并且这类算法并没有解决不同子信道间噪底差异大对检测性能产生影响的问题。上述算法中多数算法对所有信道设置的都是相同的检测门限，近年来，有较多研究者提出了基于能量检测的双门限频谱感知算法[11-13]，采用双门限值对信道进行判决的同时，对能量值处于双门限之间的情况进行相应的处理，能有效地提高检测性能。文献[11]提出了差分双门限能量检测算法，先设定2个门限，当能量值在2个门限之外时，依然采用传统的能量检测算法进行判别，当能量值在2个门限之间时，根据差分能量检测原理计算出一个新的门限值，通过将能量值与新门限值进行比较完成判别。该算法在检测性能上有所提升，但是并未解决不同子信道间噪底差异对检测性能产生影响的问题。文献[12]提出了基于形态学运算的双门限自适应信道检测算法，首先利用形态学运算来估计信道噪声基底，将噪声基底减去以后，采用最小-最大噪声方差来计算双门限，当能量值处于2个门限之间时，采用模糊理论进行判定。该算法能够在噪声起伏较大的背景取得了较好的检测效果，检测概率高于传统双门限算法和基于差分运算的双门限算法，但其基于模糊理论的判决条件以及插值算法不适合在FPGA上实现，将会耗费大量的硬件资源，这样将降低数字信道化接收机的处理速度。文献[13]提出了一种自适应双门限的双检测长度的子信道检测方法，以信道环境因子ε来表示信道的环境质量，通过ε来自适应得到双门限值，通过双门限值来对信道进行判定。该算法相比于能量算法在性能上得到提升，但该算法相对于传统能量算法而言也较为复杂。针对上述问题，本文提出了基于多级差分运算的自适应双门限信道检测算法。

1 子信道输出信号的数学模型

由于动态数字信道化接收机是先将接收到的信号经过均匀划分的数字滤波器组进行滤波实现子信道划分，然后对每个子信道的信号采用频谱感知的方法实现信道判别，再根据判决结果构造新的数字滤波器组，因此本文讨论的是经过均匀划分的数字滤波器组的子信道信号，其结构示意图如图1所示，yk[Mn]为第k个子信道信号(从0开始计数)。 由 于 是将接收到的信号经过AD采样数字化后输入到滤波器组中，所以输入到滤波器组的信号为离散的数字信号x[n]。第k个信道的输出为：

令 N满 足 N=KP，m=r+pK， 其 中 r=0,1,…,K-1，p=0,1,…,P-1。

令第r路多相滤波器结果为：

可看出除了载波差异外，子信道输出信号与原信号有相似的数学表示形式，只是原信号为实信号，子信道输出信号为复信号，但是子信道输出信号仍然携带原信号的调制信息。本文就是利用此特性来对子信道的输出信号进行信道检测。

图1 基于多项滤波结构的数字信道化接收机

2 基于多级差分的自适应双门限信道检测

由于子信道输出信号为复信号，因此在进行信道检测之前，需先对这个复数信号求模，得到实数信号，也就是信道的能量值，那么第k个信道在i时刻的能量值为Hk(i)。由于采集的信号通常含有噪声和各类干扰信号，因此需要对每个信道的能量值进行数据平滑处理，提高能量值的信噪比。本文采用移动平滑处理方法[14]，该方法计算简单，速度快，效果也较好。对于第k个信道，设Yk(i)为i时刻平滑后所得到的新的能量值，其计算公式为：

式中，m为平滑的点数，本文取16点平滑处理，原因在于16为24，在FPGA上实现时，可以使用移位处理进行实现，不需要用到除法运算，而16点相对23(8点)与25(32点)而言较为合适。

2.1 多级差分法

对于每一个子信道，当只有噪声信号时，各采样时间之间的能量差值较小，而当有信号存在时，信号到来时刻的能量值与信号到来之前的噪声能量值差值较大。对于第k个信道，从i时刻到i+1时刻的能量差值为：

式（6）为一阶差分公式。由于信号到来时有上升时间，然后信号再维持一段时间，所以本文在对单个信道进行信道判别时，采用多级差分求能量差值，这样求解出来的能量差值具有一个较高的峰值，对这个峰值进行检测就能求出该信道的一个门限值。对于第k个信道，采用多级差分公式求能量差值的公式为：

式中，m为差分级数，差分级数的选取原则为：选取的级数值要略大于信号上升时间的采样点数。本文取16级，与平滑点数相对应。在实际应用中，可以根据实际信号的上升时间大小，选取适当的级数。

2.2 多级差分法求门限

由于采用公式(7)求得的能量差值在有信号到来时会得到一个较高的峰值，这个峰值点所对应的能量值就是信号在某一时刻(具体哪一时刻跟选取的差分级数有关)的能量值，因此可以采用这个能量值的1/2作为信道判别的一个门限值λk1，此门限值将成为找到下一个峰值前的门限值。在找到任何一个峰值前，将给λk1赋一个较大值，比如232次方。所以峰值点的求取是求取门限值的关键。本文借鉴文献[14]求取最佳峰值的方法来求取能量差值的峰值点。具体方法如下：对于第k个信道而言，对差值进行16点平滑处理后得到新的能量差值信号Dk(i)，相邻两点之间差值标记记为 fk(i)，如 果 Dk(i+1)＞H且Dk(i)＞H且Dk(i+1)＞Dk(i)，fk(i)=1；如 果 Dk(i+1)＞H且Dk(i)＞H且Dk(i+1)＜Dk(i)，fk(i)=-1；如果 Dk(i+1)＞H且Dk(i)＞H且Dk(i+1)=Dk(i)，fk(i)=0；其 他 情况下，fk(i)=-2。其中H为一个固定值，其一般是根据AD采样前的信号增长6 dB在信道中所产生的能量差值增长的数值来确定。当发现出现fk(i)=0或者出现fk(i)=1和fk(i+1)=-1时，往前数fk存在m个连续的1，往后数fk存在 m个连续的-1，那么i时刻即为峰值点所在的时刻。其中m可以根据实际情况进行选取，本文选取m=16，正好与级数值相对应。

2.3 自适应双门限协作信道检测算法

考虑到采用多级差分法求取得到的门限值有可能存在不可靠的情况，因此本文采用双门限能量检测的方法来提高检测结果的可靠性。对于每一个信道都设置2个门限值，对于第k个信道而言，假设2个门限值为 λk1和 λk2，如果能量值 Yk(i)≥ λk1并且 Yk(i)≥λk2，那么第k个信道的i时刻就有信号存在，其他情况就认为信号不存在。其中门限λk1为多级差分法求取得到的门限值，上文已经给出其求解方法。而门限λk2为底噪值的4倍，其中底噪值求解方法如下：随机产生一个0～256之间的随机数，以这个随机数为间隔选取能量值，在积攒够256个能量值后求取第平均值Mold，后面每选取到一个能量值Y就利用以下公式求取新的平均值：Mnew=(Mold×255+Y)/256，在下一次求取平均值时取Mold=Mnew，每求取得到一个新的平均值就替换一次λk2。由于这2个门限值的求取都是针对每个单一信道而言的，因此本文的方法可以较好地克服不同子信道之间噪声基底差异对信道判别性能的影响，并且能够进行并行运算，即各个信道同时进行门限的求取与信号存在与否的判断，提高了运算的速度。为了降低双门限误判的概率，本文在通过双门限比较判别信号存在与否的基础上增加了一个判别标准，就是连续5个时刻判别信号存在才认为这些时刻信号存在，否则认为这些时刻信号不存在。

因此基于多级差分的自适应双门限信道检测方法的求解步骤如下：

步骤1：根据数字信道化接收机的原理，求取出各个信道的能量值；

步骤2：对每个信道，采用移动平滑处理方法对能量值进行降噪处理；

步骤3：对每个信道，采用多级差分法求取出能量差值，然后采用寻找最佳峰值的方法求取出能量差值中的峰值点，再根据峰值点求出门限值λ1；

步骤4：对每个信道，求出该信道的底噪值，得到门限值 λ2；

步骤5：对于每个信道，又如果能量值既大于门限值λ1又大于门限值λ2，那么在这个时刻就认为信号存在；其他情况下，就认为信号不存在。判别是否连续5个时刻信号存在，是则认为这些时刻信号存在，否则认为这些时刻信号不存在。

由前面介绍的求解步骤可知，本文方法是基于流水线思路进行设计的并且计算简单，易于在FPGA上实现，具有工程实践的价值。

3 实验仿真与分析

为了验证本文算法的正确性与有效性，采用蒙特卡罗方法进行Matlab仿真。假设AD以1 GHz的采样率对实信号进行采样，那么动态数字信道化接收机的瞬时带宽为0～500 MHz（奈奎斯特采样定理）。设分析滤波器均匀划分为32信道，那么有效信道为16信道。由于信道化能够滤除带外噪声，提高信噪比，因此在工程实践中，信道化是脉冲检测一个非常重要的步骤。信道检测性能的优劣直接影响到脉冲检测结果的好坏，因此采用脉冲信号来验证本文算法的正确性与有效性。图2、图3给出的是在接收机覆盖的频段内的一个带宽为40 MHz、频率为160～200 MHz的LFM信号经过数字信道化接收机后在各个信道的能量值和能量差值，由于只有16个有效信道，因此只显示前16信道。为了观察方便，设置脉宽为2 μs，并使用awgn函数加入了信噪比为15 dB的高斯白噪声，取其中一个脉宽进行显示。

由数字信道化接收机原理可知，带宽为40 MHz、频率为160～200 MHz的LFM信号将落在5、6、7信道(从0开始计数)，与图2中的显示情况相符。由图2中各信道的能量分布可以看出，当只有噪声信号时，各采样时间之间的能量差值较小，而当有信号存在时，信号能量值与噪声能量值差值较大，因此采用多级差分算法可以得到具有峰值的能量差值。在图3中，虽然各个信道的能量差值都有峰值出现，但是在5、6、7信道中的峰值上升时间与下降时间持续的时间较其他信道的要长，并且峰值的大小也较其他信道的要大很多，能够较好地进行区分与提取。由图2、图3可知5、6、7信道中的峰值所在时刻正好是信号所在的时刻，由此求取出来的门限值较为靠谱。

图2 LFM信号在各个信道的能量值

本文方法的难点和障碍是找到正确的能量差值峰值点。只有噪声信号时，各采样时间之间的能量差值较小，产生的峰值也较小，峰值点的上升时间与下降时间短，而当有信号存在时，信号能量值与噪声能量值差值较大，所产生的峰值也较大，峰值点的上升时间与下降时间长，并且峰值点的上升时间与下降时间还与信号的持续时间有关，因此寻找峰值点时的参数m的选取最为关键，如果m较小就会找到噪声的峰值点，如果m较大就会漏掉信号的峰值点，本文对m的取值进行了仿真。同样以带宽为40 MHz、频率为160～200 MHz的LFM信号来对m的取值进行仿真，分别选取脉宽为1 μs和脉宽为10 μs、重复周期都为100 μs的2个信号，通过500次蒙特卡洛仿真实验得到如图4所示的结果。

图3 LFM信号在各个信道的能量差值

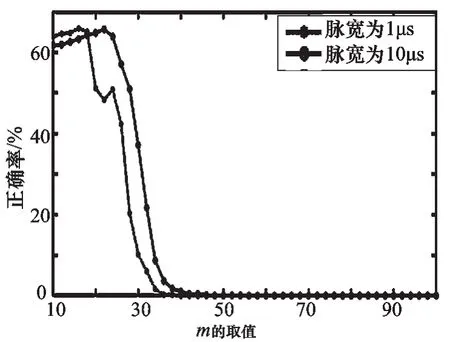
图4 m取值对正确率的影响

由于采用脉冲信号来验证本文方法的优劣，仿真时能预知正确结果，因此本文采用不同信噪比条件下的正确率来作为衡量信道检测的性能指标。本文正确率的计算方法为：在任一时刻，有信号的信道检测出信号的同时无信号的信道没有检测出信号才认为这一时刻信道检测正确，对62500个时刻的信号进行信道检测，最后求得一个正确率。由图4可知，对于1 μs的信号，m＜16之前正确率不断上升，在m＞16以后，正确率呈下降的趋势；对于10 μs的信号，m＜22以前正确率不断上升，在m＞22之后，正确率呈下降的趋势，因此本文取m=16。

为了评估本文算法的性能，通过仿真实验将本文方法与基于形态学运算的检测算法、差分能量检测算法进行对比。首先，假设输入信号为带宽为40 MHz、频率为 160～200 MHz的 LFM 信号，脉宽为 10 μs，重复周期为100 μs，通过500次蒙特卡洛仿真实验，对比三种方法在不同信噪比条件下的正确率，所得结果如图5所示。由图5可知，本文方法的抗噪性能最佳，在11 dB以下正确率比其他2个方法都高，在11～14 dB之间比其他2个方法稍低，但正确率呈上升趋势，在14 dB以后正确率又高于其他2种方法，并且算法在设计时按照流水线技术进行设计，便于在FPGA上实现，可以提高算法的运行速度且易于工程实现。可见本文方法在信道检测上具有一定的优越性。

然后，假设接收机覆盖的频段内有三个常规信号，分别为：频率为 160 MHz，脉宽为 1 μs，重复周期为100 μs的信号；频率为 220 MHz，脉宽为 2 μs，重复周期为 100 μs的信号；频率为 410 MHz，脉宽为 5 μs，重复周期为100 μs的信号。通过500次蒙特卡洛仿真实验，对比三种方法在不同信噪比条件下的正确率，所得结果如图6所示。由图6可知，三种方法对常规信号的检测性能与对LFM检测的检测性能基本一致，同样体现了本文方法在信道检测上的优越性。

图5 不同信噪比条件下对LFM信号检测的性能比较

图6 不同信噪比条件下对常规信号检测的性能比较

4 结束语

本文提出了基于多级差分的自适应双门限信道检测算法，该算法针对每个信道，首先根据多级差分算法求得的峰值自适应得到门限1；然后根据底噪估计算法自适应得到门限2；各个信道中每个时刻的能量值若大于其当前时刻的门限1和门限2，就认为这个时刻该信道有信号存在，当连续多个时刻检测到信号存在时才认为这些时刻有信号存在。由于求取的2个门限值都是针对单一信道而言的，因此本文的方法可以较好地克服不同子信道之间噪声基底差异对信道判别性能的影响。本文算法计算快速简单，可以进行实时处理，并且算法在设计时按照流水线技术进行设计，便于在FPGA上实现，可以提高算法的运行速度并易于工程实现。仿真结果表明，与基于形态学运算的检测算法、差分能量检测算法相比，本文算法在低信噪比和较高信噪比条件下都有较好的检测性能，具有一定的优越性。■