一种线路勘察勘探点里程和偏移量智能解算的方法
2020-04-11胡振联吴学林
刘 艺 胡振联 吴学林
(机械工业勘察设计研究院有限公司,陕西 西安 710043)
1 问题的提出
在线路工程勘察过程中,一旦线路调整,将导致勘探点里程和偏移量也随之不断地变化,在CAD中使用人工手动反复解算勘探点里程和偏移量的工作量很大。我们实现了一种智能解算的方法,能够提高工作效率和解算精度,现在本文中介绍这种方法的原理和实现方法。
2 相关概念的介绍
勘察专业确定一个勘探点的空间位置常常用坐标和高程来描述。但在线路勘察中的勘察对象是空间内的线状构筑物,例如铁路、公路和管线等。这种情况下,工程上就会以线状对象为参照,采用里程、偏移量和高程来确定一个勘探点的空间位置。
使用坐标和高程或者使用里程、偏移量和高程来确定勘探点的位置这两种方法只是在平面位置的描述上不同,而高程却是相同的,所以接下来本文仅讨论勘探点平面位置的问题。画图解释一下上述概念。
如图1所示,粗实线为带有里程的线状勘察对象,平面中布置有一个勘探点A。如果要确定A的平面位置,除了用坐标来表示以外还可以用里程和偏移量来表示。使用后者表示A的平面位置的原则为:首先通过A点对线路c作垂线,垂足为B(通常只有一个垂足,如果有多个垂足则选择AB长度最短的B点作为垂足),那么B点在线路c上的里程就是勘探点A的里程,线段AB的长度就是勘探点相对于线路的偏移量。偏移量的正负按如下原则确定:站在线路上,面向大里程方向,左边为负,右边为正,那么图1中勘探点A的偏移量为一个负值。
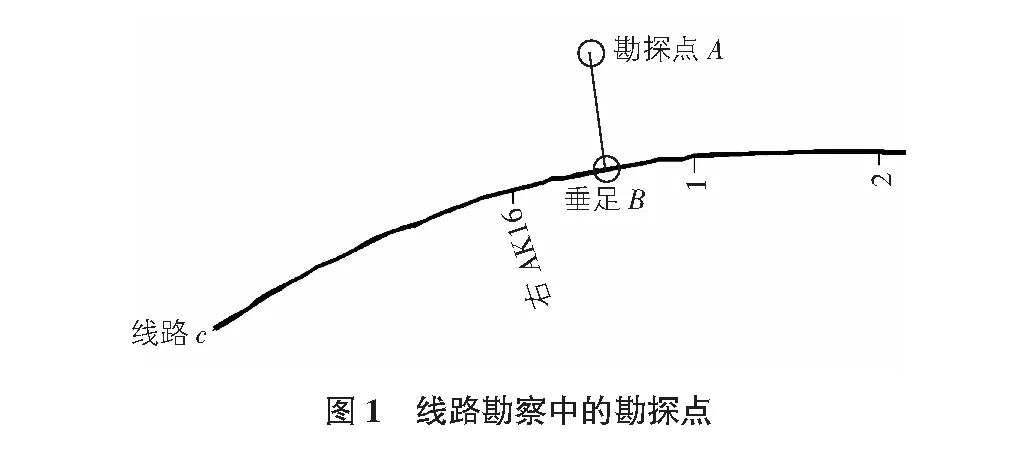
基于上述定义,一个固定位置的勘探点A的里程和偏移量会随着线路的平面位置或者里程的变化而变化。当勘探点数量众多时,手动解算里程和偏移量的工作量非常繁琐。面对这种机械的工作,我们考虑采用电算的方法来解决。
3 问题的抽象化
我们需要抽象化这些工程元素以方便使用计算机来模拟。
对于线路c,我们使用了带有方向的多段线对象来模拟。这种带有方向的多段线实际上是一个数组{(x1,y1,z1),(x2,y2,z2),…,(xn,yn,zn)},这个数组中每个元素都包含xi,yi,zi三个实型变量,它可以描述空间中的一个点。那么多段线表示空间已知的n个点,这n个点按照数组中元素排列的先后顺序连接起来形成一个有方向的多段线,它的起点为第1个点,终点为第n个点。
对于线段AB,我们使用了线段对象来模拟。线段对象可以用一个包含2个元素的数组来表示:{(xA,yA,zA),(xB,yB,zB)}。
对于散点元素,例如勘探点A,垂足B等等,我们可以使用一个点对象来表示:(xi,yi,zi)。
4 算法介绍
4.1 垂足的确定
对于已经给定的勘探点A和线路多段线c需要用如下方法来确定垂足B:连接A点和多段线c各节点,得到一组线段:AC1,AC2,…,ACn。解算这一组线段与多段线c的夹角。当多段线上某相邻两个节点Ci和Ci+1与A点构成的三角形符合式(1)时,可以判定A点在多段线c上有垂足,且垂足位于线段CiCi+1上。
∠ACiCi+1≤90°且∠ACi+1Ci+2≥90°
(1)
4.2 偏移量的确定
当一个勘探点A在多段线c上存在垂足B的时候,我们需要判断偏移量的正负以及数值。
为了方便代码实现,我们使用经典几何与解析几何的方法来求解偏移量的正负和数值,方法如下:1)过Ci点作向右的水平线CiD,求解∠Ci+1CiD的角度β,见图2。2)将三角形ΔACiCi+1按Ci点顺时针旋转角度β。旋转之后,线段CiCi+1必然为一条水平线,且Ci的x坐标一定小于Ci+1的x坐标,见图3。3)比较旋转之后点A与点Ci的y坐标值。若yA>yCi,则偏移量为负;若yA=yCi,则偏移量为0;若yA yA-yCi即可直接作为偏移量的结果用于输出。 勘探点A在多段线c上的投影里程就是垂足B点在多段线c上的里程。 已知垂足B位于线段CiCi+1上,则B的里程可以按下式求得: 其中,L为垂足在多段线上的里程;H为多段线的起点里程。 将第4节介绍的算法画成程序框图如图4所示。 考虑到工程制图常用的工具软件是Autodesk公司开发的AutoCAD工具软件,故本算法的实现使用了VBA语言。在本文编写之前,我们已经写出了可以用于工程的数据健壮的完整程序。 显然,程序框图中最核心的代码是步骤2和步骤3。现将编译通过的相关代码列于以下: 步骤2:获取多段线上的点。 If TypeOfreturnObjIsAcadLWPolyline Then n=(UBound(returnObj.Coordinates)+1)/2 ElseIfTypeOf poly Is AcadPolyline Then n=(UBound(returnObj.Coordinates)+1)/3 End If ’以上代码得到多段线有n个点结束 ’以下代码用于搜索多段线符合要求的段落 ’选取一个钻孔 Dim w As IntegerDim ntxt As Integerntxt=0 For w=0 To 2 On Error GoTo err1 a=ThisDrawing.Utility.GetPoint(,"拾取一个点:") For i=1 To n-1 ’MsgBox("下标已经到:"&i) judge=ifin(a,returnObj.Coordinate(i-1),returnObj.Coordinate(i)) If judge=0 Then ElseExit ForEnd If Next ’以上代码完成’得到里程 Dim countformile As Integer Dim mile As Doublemile = 0 ’MsgBox (i) For countformile=1 To i mile=mile+distant(returnObj.Coordinate(countformile-1),returnObj.Coordinate(countformile)) Next mile=startmile.text+mile-Sqr(distant(returnObj.Coordinate(i),a)^2-offset^2) Dim strmile As String strmile=CStr(Format(Round(mile,2),"0+000.00")) result.text=strmile ’得到里程结束 步骤3:解析偏移量。 Public Function distofline(a,b,c As Variant) As Double ’点到线段的距离公式,a是点,b,c是线段的段点 ’根据这些点创建二维多段线 Dim pi As Variant Dim polyObj As AcadLWPolyline Dim vertices(0 To 5) As Double Dim offset As Double vertices(0)=a(0):vertices(1)=a(1) vertices(2)=b(0):vertices(3)=b(1) vertices(4)=c(0):vertices(5)=c(1) Set polyObj=ThisDrawing.ModelSpace.AddLightWeight Polyline_ (vertices) polyObj.closed=True offset=(polyObj.Area)*2/Sqr((b(0)-c(0))*(b(0)-c(0))+(b(1)-c(1))*(b(1)-c(1))) ’判别偏移量的正负 Dim aa(0 To 2) As Double Dim bb(0 To 2) As Double Dim cc(0 To 2) As Double aa(0)=a(0)aa(1)=a(1)aa(2)=0bb(0)=b(0)bb(1)=b(1) bb(2)=0cc(0)=c(0)cc(1)=c(1)cc(2)=0 Dim line1 As AcadLine Dim line2 As AcadLine Set line1 = ThisDrawing.ModelSpace.AddLine(aa, bb) Set line2 = ThisDrawing.ModelSpace.AddLine(aa, cc) polyObj.Rotateaa, -line1.angle ’ MsgBox (polyObj.Coordinate(1)(0) & ";" &polyObj.Coordinate(1)(1) &Chr(10) &polyObj.Coordinate(2)(0) & ";" &polyObj.Coordinate(2)(1)) Dim lineforang As AcadLine aa(0) = polyObj.Coordinate(1)(0) aa(1) = polyObj.Coordinate(1)(1) bb(0) = polyObj.Coordinate(2)(0) bb(1) = polyObj.Coordinate(2)(1) Set lineforang = ThisDrawing.ModelSpace.AddLine(aa, bb) If lineforang.angle>Atn(1) * 4 Then offset = Abs(offset Else offset = -Abs(offset) End If ’正负判别结束’ distofline = offset ’消除辅助线 lineforang.Delete line1.Delete line2.Delete ’ polyObj.Rotateaa, line1.angle polyObj.Delete ’辅助线消除完毕 End Function 程序框图中的步骤8专门用来处理一些特殊情况。有如下几种特殊情况和工程相关。 如图5所示,从勘探点A是无法对线路c作垂线的。当然这种情况也是工程上不允许的。试想,无论是铁路还是公路,都不会以角度的方式来拐弯。出现这种情况通常是技术员用多段线拟合线路时在转弯处的点间距太大所致。解决的方法就是增加描线的节点密度,如图6所示。 如图7所示的情况,勘探点A在线路c上有多个垂足。工程上这也是不可能的,但在理论上,这种情况却非常有可能。处理的方式就是选择偏移量绝对值最小的那个垂足。 如果用多段线来拟合实际线路,在直线段是不存在偏差的,可是在线路拐弯处则会不可避免地出现偏差,如图8所示。 因为无论多段线的节点多么密集也无法拟合成弧线。对于这种情况的处理方式如下。 首先要满足勘察的精度。规范允许勘探点在实际施工中进行必要的挪动。相比之下线路上的弧形拐弯带来的里程偏差则十分微小。 其次,当多段线拟合的线路太长,拐弯太多,检查程序输出的里程和线路上标注的实际里程的差值已不能满足规范要求时,可以采用打断多段线的方式来处理。我们只需要准确地输入打断处的里程作为第二条多段线的起始里程,那么误差就会归零。这种方法同样可以用来处理线路上的短链或长链问题。 上文说到我们已经开发出可用于工程实践的工具软件,现演示如下。 输入多段线拟合线路的起始里程然后点击获取里程和偏移量,详见图9。点选勘探点即可输出勘探点的里程和偏移量,详见图10。 1)因为指定对象,所以这种算法可以用于非常复杂的平面图,图中复杂的底图元素并不会对本算法的计算过程产生干扰。2)该方法是对AutoCAD采用VBA工具的二次开发,所以我们得到的成果具有跨操作系统和跨CAD版本的广泛兼容性。3)使用VBA工具开发,可以提供友好的用户界面。软件的友好性、易用性和数据的健壮性都要优于lisp代码使用命令行人机交互的方式。 1)本算法虽然用于对平面图中勘探点里程和偏移量的解算,但是算法中预留了高程数据接口,在有需要的情况下可以用来处理三维问题。 2)还可以考虑采用批处理方式将获取数据直接输出到各种勘察软件预留的接口内从而进一步提高工作效率。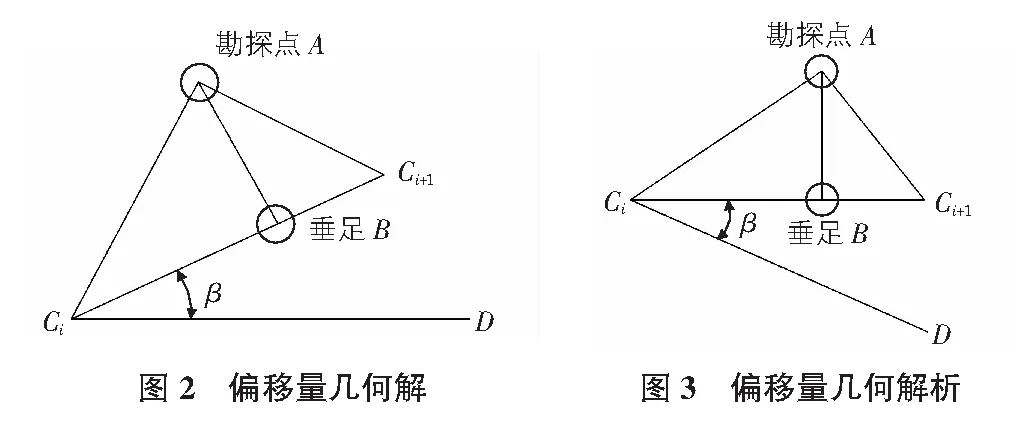
4.3 里程的确定
5 算法的实现
5.1 程序框图
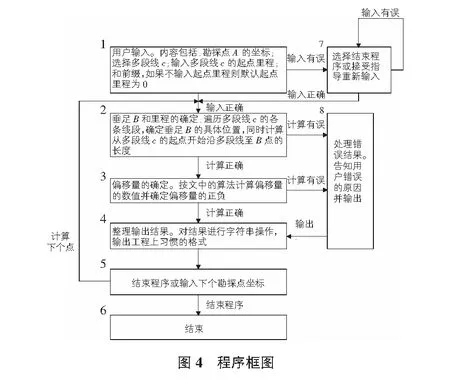
5.2 代码实现
6 几种特殊情况的讨论
6.1 多段线上没有勘探点的垂足
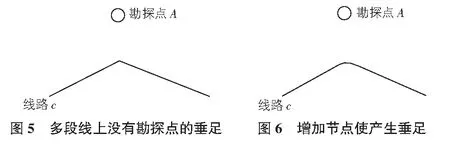
6.2 多段线上有多个垂足
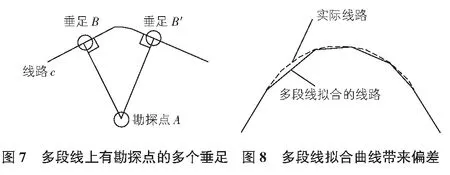
6.3 精度问题
7 实例演示


8 算法特点及展望
8.1 算法特点
8.2 展望
